基于本地测量的高比例新能源电力系统不平衡功率估算与附加功率控制策略

张军六，李佳朋，唐 震，陈秋逸，郝丽花，李宇骏，许 昭

(1.国网山西省电力公司电力科学研究院，山西 太原 030001；2.西安交通大学电气工程学院，陕西 西安 710049；3.香港理工大学电气工程学院，香港 999077)

近年来，新能源发电以其清洁、可再生等优势得到了大力发展，新能源占比日益提高[1-4]。截至2019年底，中国风电和光伏发电累计装机分别达到2.1亿千瓦和2.04亿千瓦，新能源装机并网容量居世界首位，部分地区新能源出力占比已逾50%[5]。然而，电力电子换流器型电源与系统频率间缺乏耦合，难以在系统受扰后为其提供功率支撑。随着传统同步电源被换流器型电源逐步替代，电力系统惯量水平日益下降，系统动态过程中频率变化快，容易超出规定频率波动范围[6-7]。因此，高比例新能源电力系统具有低惯量特点，如何保证该系统的频率稳定成为挑战。

电力电子换流器控制具有灵活性高、响应速度快等特点，通过改变换流器的控制特性可以改善低惯量新能源电力系统的频率响应。附加控制的核心在于从交流系统提取相应的扰动信号(系统频率、阻尼相关信号等)作为控制器的输入，通过设计合理的控制律，将扰动信息加到换流器功率调制端口，从而改变端口传输功率，达到改善交流系统暂态稳定、抑制系统振荡、提供紧急功率支援的目的。通常而言，提升系统频率稳定的换流器控制可以大体上分为下垂控制与虚拟同步控制。下垂控制使换流器传输功率响应交流系统频率扰动，在频率突变时向交流系统提供功率支撑，从而抑制频率偏移。此外，通过改变下垂系数可以方便地改变功率分配，故下垂控制在多端系统中具有发展优势[8-11]。文献[8]通过施加电压—频率下垂控制，使直流系统传输功率可以响应交流系统的频率变化，利用多端直流系统实现了异步电网间的功率互济；文献[9]进一步考虑了直流系统中多端口间功率控制的耦合特性，并通过设计解耦控制算法实现了各端口功率的独立调制。尽管下垂控制结构简单、易于实施，但其仅在系统频率偏移较大时才能提供较强的功率支撑，动态特性有待提高。为了克服这一缺点，国内外学者对虚拟同步控制进行了大量研究[12-16]。虚拟同步控制通过设计控制方程使换流器模拟同步发电机的机电动态过程，从而给交流系统提供虚拟惯量与虚拟阻尼支撑。文献[12]对双馈风电机组利用风轮旋转动能参与调频的能力进行量化，通过施加虚拟惯量调频控制环改变风电机组的电磁转矩，实现风轮储能的快速吞吐；文献[13]考虑直驱风机背靠背直流母线侧配置的储能，利用风轮机械动能实现了虚拟惯量支撑；文献[14]讨论了虚拟惯量控制中频率微分信号获取慢、易引起谐波放大的问题，并提出了基于级联二阶广义积分器—锁频环评估频率信号的虚拟惯量控制策略；文献[15]研究了虚拟惯量与虚拟阻尼对微电网频率稳定的影响，提出了微电网虚拟惯量与虚拟阻尼参数优化设计方法。然而，虚拟同步控制继承了同步发电机的机电暂态特性，如何匹配虚拟惯量与虚拟阻尼等控制参数以抑制系统的机电振荡成为难点。此外，多个虚拟同步机接入后，电网的动态特性愈加复杂，机组间存在耦合与相互激励，不利于虚拟同步控制的分析与设计。此外，以上频率控制器的设计都基于暂态频率的变化，无法利用换流器的快速功率调制，导致在扰动初期，频率变化迅速，频率偏移较大，暂态频率稳定性问题无法得到较好地解决。

为解决上述问题，本文基于附加功率控制框架提出了适用于高比例新能源电力系统的频率稳定提升控制方法。如何快速估算系统的不平衡功率，从而给定补偿功率的目标值，是附加功率控制的核心。为快速估算事故发生时系统的不平衡功率，可以通过系统惯量中心频率变化率与系统等值惯量计算获得。具体而言，为了避免通讯延时，本文采用本地频率曲线二阶导数零点连接得到的分段线性曲线近似估算系统惯量中心频率的变化。而系统等值惯量的评估则基于同步惯量与系统功率变化间的数学关系，通过历史事故分析间接获得。确定系统不平衡功率后，新能源机组与同步机组出力按照其各自占比进行分配，附加控制快速调节新能源接入换流站的功率指令进行功率补偿。

本文的主要贡献可以体现在以下方面。首先，针对现有系统惯量中心频率计算方法依赖于通讯、难以满足快速频率控制要求的问题，提出了基于本地频率曲线二阶导数零点检测的系统惯量中心频率估算方法，从而无需通讯就可以估算出系统惯量中心频率。其次，针对已有系统惯量水平计算方法中缺乏考虑负荷及电力电子设备对惯量的贡献的问题，提出了利用系统同步惯量与事后统计信息的系统惯量估算方法，可以更好地应用于高比例新能源电力系统。最后，通过系统惯量中心频率变化与系统惯量估算系统受扰时的功率缺额，并设计了相应的附加功率控制，从而为高比例新能源电力系统提供惯量支撑。

本文对附加功率控制的改进主要体现在由频率-功率控制特性转变为直接基于系统不平衡功率估算进行补偿，且所提方法原理简单，实施不依赖于通讯，对高比例新能源电力系统具有较好的适应性。数值仿真将所提控制与传统下垂控制进行对比分析，验证了所提策略可以快速响应频率扰动，更好地抑制系统频率跌落或突增。

1 无需通讯的系统惯量中心频率估算方法

事故发生时系统的不平衡功率是未知的，为了在系统惯量响应阶段估算出系统的不平衡功率，本文通过系统频率变化率与系统惯量对其作间接估算，主要介绍了所提系统频率变化率估算方法的基本原理。

当系统经受干扰后，同步发电机间存在相互摇摆，因此电力系统中在多个频率振荡。为了便于描述多机系统的频率响应过程，常在惯量中心(center of inertia，COI)坐标下对系统进行建模分析[17]。系统COI频率可由如下方程获得：

(1)

式中N为系统内发电机数量；Hi、fi分别为第i台发电机的惯量常数和频率。由式(1)可知，计算系统COI频率需要获取系统内每台发电机的频率，故COI频率的测量依赖于广域测量系统(wide-area measurement system, WAMS)。对于输电网络，系统级通信的时间一般为分钟级。而本文所研究的快速功率调制需要在事故发生的1 s内完成不平衡功率的估算。在这个时间尺度内，将各结点测量数据上送给调度中心计算系统COI频率，并将指令返回给本地，是不切合实际的。因此，需要探索仅基于本地测量的COI频率估算方法，以解决传统惯量中心频率计算方法无法满足功率调制快速性要求的矛盾。

本文基于发电机频率响应曲线的特性，提出了一种无需通讯的系统COI频率估算方法，具体说明如下。图1为经典的两区域系统，两区域分别用2台同步发电机表示，记为SG1与SG2，其电压与功角分别用U1、U2与δ1、δ2表示，R、X分别为联络线的等效电阻与电抗。

图1 典型两机系统Figure 1 typical two-source system

系统经受干扰后，2台发电机的转子运动可描述为

(2)

式中H1、H2分别为SG1、SG2的惯量常数；f1、f2分别为SG1、SG2的频率；Pm1、Pm2分别为SG1、SG2的机械功率；Pe1、Pe2分别为SG1、SG2的电磁功率。

同时，结合网络方程可以计算出2台发电机的电磁功率变化量为

(3)

式中δ12为2台发电机转子的功角差，δ12=δ1-δ2。

在惯量响应阶段，可认为原动机出力不发生变化。式(2)中的2个等式分别对时间t求导，可得：

(4)

结合式(3)与式(4)，并忽略功率扰动时交流系统结点电压的微小变化，有

(5)

式中f12为2台发电机的频率差，f12=f1-f2。

令式(5)中2个等式的左边分别为零，可得f12= 0，也即此时系统内发电机频率相等。结合式(1)与式(5)，有

(6)

式(6)说明，当发电机频率对时间的二阶导数为零时，系统内所有发电机频率相等，且此时发电机频率曲线与系统COI频率曲线重合。简言之，系统COI频率必过任意发电机频率曲线二阶导数零点。

对于一般的多机系统，可以用两群系统进行等值[18]，从而将上述证明推广到更一般的系统中。在频率暂态过程中，本地频率围绕系统惯量中心频率小幅波动，并最终在系统内所有发电机频率趋于一致时收敛于系统惯量中心频率曲线[19]。大量仿真分析表明，当本地频率曲线呈凹性时，本地频率曲线基本位于系统惯量中心曲线上方；而当本地频率曲线呈凸性时，本地频率曲线基本上位于系统惯量中心曲线下方。因此，在本地频率曲线的拐点处，本地频率曲线应与系统惯量中心频率曲线非常接近。这是由于发电机间转子摇摆的振荡模态可以用衰减正弦函数表示，当发电机频率二阶导数为零时，发电机频率近似与其机间振荡的摇摆中心频率(系统惯量中心频率)一致。利用这一性质，将本地测量频率曲线二阶导数零点依次连接，得到的分段线性曲线可以近似代替系统COI频率曲线，从而避免了获取COI频率时对通讯的依赖。

两区域系统受扰后的频率响应如图2所示。其中，红色的点线由SG1频率曲线获得，每个点即SG1频率曲线的二阶导数零点。由图2可知，频率暂态过程中，发电机SG1的频率曲线围绕系统COI频率振荡，而本文所提的分段线性近似曲线与COI频率曲线几乎完全重合，从而验证了该方法的有效性。

图2 两机系统受扰后的频率响应Figure 2 Frequency response of the two-source system after power disturbance

2 系统等值惯量估算方法

惯量是电力系统重要的物理属性之一，反映了系统遭受干扰后频率变化的快慢程度，系统惯量越大，则受到同样大小的功率干扰后频率变化越慢，单位时间内变化幅度越小。系统惯量可以大体上分为同步惯量、负荷惯量与新能源惯量[20]。其中，同步机提供的惯量具有明确的物理意义，对其评估较为容易，而负荷与新能源的惯量响应较复杂，不易直接计算。因此，本文利用同步惯量和系统功率变化间接估算系统的惯量水平。

第i台同步电机的惯量常数由该发电机同步转速下存储的动能与电机额定容量的比值决定，即

(7)

式中Ji为第i台发电机的转动惯量；fn为系统额定频率。结合发电机的频率变化率，可以计算第i台发电机的出力变化为

(8)

系统同步惯量HG和发电机总共的出力变化ΔPG可按如下计算得到：

(9)

当系统中仅含同步惯量时，结合式(1)、(8)、(9)可得：

(10)

相似地，在计及系统中异步电机提供的惯量与新能源提供的虚拟惯量时，应有：

(11)

式中Hsys为系统等值惯量；ΔP为系统不平衡功率。由于ΔP计及了系统内非同步元件的功率变化，有ΔP>ΔPG。

结合式(10)、(11)，可得到系统等值惯量的计算公式为

(12)

式中HG和ΔPG需要根据频率事件后的测量记录结果，统计在投发电机的惯量与其出力变化量得到；ΔP可通过事故分析获得。频率事故后，统计计算得到的系统惯量将成为下次频率事件时系统等值惯量的参考值。值得注意的是，式(12)近似认为系统等值惯量与同步惯量之比等于系统遭受干扰并恢复稳态时系统功率变化与发电机功率变化间的比值。实际上，在系统遭受干扰后的初期，整个系统的不平衡功率很难快速获得。而式定义的系统等值惯量可以用于粗略计算系统不平衡功率的大小，这对后续稳定提升控制的设计有重要意义。由于后续控制并不需精确计算出ΔP，系统惯量亦不必非常精确，故所提的等值惯量估算方法是合理的。

3 附加功率控制策略

随着新能源占比的不断增加，电力系统惯量水平逐渐下降，系统受扰后频率稳定性问题突出。为了保证系统的频率稳定，可利用新能源接入换流站的快速功率调节为交流系统提供紧急功率支持。具体地，可改变换流器的外环功率控制特性，使新能源的输出功率响应交流系统频率扰动，这类控制即为新能源的附加功率控制。

3.1 传统下垂控制策略

功率—频率下垂控制结构简单，可以方便为交流系统提供频率支撑。其控制率可以由如下方程描述：

(13)

图3 传统功率—频率下垂控制Figure 3 Traditional power-frequency droop control

由式(13)可知，只有当交流系统频率较额定频率偏移较大时，逆变站才能为系统提供较大的频率支撑。在系统发生频率事件初期，传统功率—频率下垂控制响应很慢，难以有效地抑制系统频率下跌或突增。此外，Kd的选定往往依赖于工程经验，如何从理论角度给出下垂系数的整定方式仍有待进一步研究。

3.2 所提附加功率控制策略

本文利用系统受扰后的频率曲线与系统等值惯量快速估计系统的不平衡功率，从而在惯量响应阶段调整新能源发电出力，以减小系统频率偏差。根据式(11)，系统不平衡功率计算公式为

(14)

为了避免噪声干扰下附加功率控制频繁改动换流器传输功率指令值，加设启动判据对频率事件进行检测：

|fPCC-fn|>Δfset

(15)

式中 Δfset为频率事件启动阈值。

当检测到频率事件后，系统COI频率按照文第1节中所提的分段线性近似方法估算。首先，计算频率的二阶差值序列，即

y(n)=(fPCC(n)-fPCC(n-1))-

(fPCC(n-1)-fPCC(n-2))=

fPCC(n)+fPCC(n-2)-2fPCC(n-1)

(16)

式中n为离散时间采样点序号；y(n)为时刻n对应的频率二阶差值点；fPCC(n)为时刻n对应的PCC点测量频率。

注意到附加功率控制关注的是事故发生初期的系统惯量中心频率变化率，可以通过检测本地频率曲线前2个二阶导数零点相连得到的直线斜率获得。因此，分段线性逼近曲线的非光滑特性不会对频率控制策略产生影响。检测二阶差值序列的前2个过零点n1、n2的条件式为

y(n)y(n-1)≤0

(17)

相应的，COI频率变化率可按下式估算：

(18)

在系统频率暂态过程中，发电机间的转子摇摆远快于系统惯量中心频率的变化过程，这是由于每台发电机的惯量都显著小于系统惯量。机间频率摇摆一次，发电机的频率曲线的凹凸性改变2次，即产生2个二阶导数零点。考虑到输电级系统的频率首摆通常在10 s左右的时间尺度[21]，保守估计前2次二阶导数零点检测完成的时间应明显小于5 s。因此，基于二阶导数零点检测的系统惯量中心频率估算方法可以满足附加频率控制的快速性要求。

系统等值惯量仍为上次事后分析获得的Hsys，其计算方法已在文第2章中介绍。将式(18)代入式(14)，可以得到系统的不平衡功率：

(19)

估算出系统不平衡功率后，可根据新能源装机容量与系统总装机容量的比值，安排新能源机组承担系统的功率缺额或盈余。结合式(14)、(18)，并考虑到新能源接入站的容量限制，新能源的出力指令值为

Pinv=

(20)

式中Pcap为换流站容量；Kr为新能源装机容量与系统装机容量之比。由于附加功率控制仅在系统频率暂态阶段起作用，可利用风机转子动能、直流电容储能以及储能系统(energy storage system,ESS)[22-23]能量调节等方式为系统提供短时的频率支撑，一定程度上避免了新能源随机性与波动性带来的影响。

本文所提控制策略如图4所示，其中包括频率事件检测、系统惯量中心频率变化率估算、系统等值惯量评估、新能源与同步机协同控制4个部分。频率事件检测通过计算PCC点的频率偏移值实现，当PCC频率与额定频率差超出阈值时，附加功率控制启动。系统惯量中心频率变化率估算基于本地测量的PCC频率的二阶导数零点检测实现，注意到所提控制方法旨在频率事件发生初期进行一次功率补偿，故只需检测前2个二阶导数零点。得到前2个本地频率二阶导数零点后，系统惯量中心频率变化率可按式(18)计算得到。系统等值惯量可通过历史事故分析确定，这是由于系统等值惯量与不平衡功率难以同时获取，故采用上次频率扰动后评估的系统等值惯量近似替代当前系统的等值惯量。根据式(12)，通过统计同步机惯量、出力变化与系统功率不平衡量，可以计算出系统的等值惯量。结合系统惯量中心频率变化率估算与系统等值惯量评估的结果，可以根据式(19)计算出事故发生时系统的不平衡功率，从而确定附加功率控制的控制目标。新能源机组与同步机组出力按照其各自占比分配，附加控制快速调节新能源接入换流站的功率指令进行功率补偿，而同步机则按照自身特性及原动机特性为系统提供频率支撑。

图4 所提附加功率控制策略Figure 4 Block diagram of the proposed supplementary power control

4 仿真分析

为验证本文所提控制策略的有效性，在PSCAD/EMTDC中搭建了如图5所示的新能源电力系统。该系统新能源装机容量占比为40%，系统特性已与传统同步电源主导的电力系统有明显区别。测试系统包含3台等值发电机，每台发电机用经典二阶模型表示，并配有相应的调速系统。负荷采用恒阻抗模型，并通过RX模型表示的架空线路与发电机连接。光伏发电集中升压后经互联换流器接入3号结点。为了平抑新能源出力的波动，在直流侧配有具备快速功率调制能力的储能系统。换流器采用功率—频率下垂控制，其与交流系统的无功交互控制为零。测试系统的主要参数如表1所示。

图5 测试新能源电力系统Figure 5 Outline of the test system with renewable energy integration

表1 测试系统主要参数Table 1 Concerned parameters of the test system

4.1 负荷突增

测试系统6号节点吸收功率突增0.4 p.u.时系统的动态过程如图6所示。当负荷突增时，由于发电机发出功率小于系统消纳功率，发电机转子减速以释放旋转动能为交流系统提供功率支撑，系统频率随即下跌。

图6 不同控制策略下负荷突增时的系统动态Figure 6 Dynamics of the test system under sudden increase of load with different control strategies

图6(a)为新能源不参与惯量响应与调频过程时系统的频率响应。由图6(a)可知，系统动态过程中，发电机频率曲线围绕系统COI频率曲线波动，发电机频率曲线二阶导数零点相连得到的分段线性曲线即为COI频率估算曲线。根据上述分析可知，本文所提COI频率估算方法所得的计算结果几乎与实际的系统COI曲线重合，很好地验证了所提频率估算方法的准确性。此外，从事故发生到检测出前2个二阶导数零点的时间间隔为0.584 s，说明所提方法可以快速估算系统惯量中心频率的变化率。图6(b)、(c)分别为下垂控制和所提控制下系统的动态过程。由图6(b)、(c)可知，由于新能源对交流系统的支撑作用，系统频率偏移明显较无附加控制时少。此外，下垂控制在系统频率偏离额定值较大时才能提供较强的功率支撑，其对应的频率最低点仍不理想(频率最低点约为0.993 2 p.u.)。由图6(c)可知，本文所提方法估算出的系统功率缺额与真实值十分接近，且所提控制策略可以在频率跌落初期迅速估算并补偿系统的功率缺额，因而对系统频率下跌有更好的抑制作用(频率最低点约为0.994 4 p.u.)。因此，所提控制策略可以改善系统受扰后的频率动态过程，提升系统的首摆稳定性。

4.2 负荷突降

测试系统5号节点消纳功率骤减0.6 p.u.时系统的动态过程如图7所示。图7(a)为新能源不响应交流系统频率变化时的系统动态过程。由图7(a)可知，负荷减小后发电机产生功率盈余，使转子加速、系统频率上升，频率最高点约为1.006 4 p.u.。从事故发生到检测出前2个二阶导数零点的时间间隔为0.403 s，满足附加功率控制的快速性要求。此外，分段线性估算曲线与真实的系统COI频率曲线十分接近，再次验证了所提COI频率估算方法的准确性。图7(b)、(c)分别为负荷突降时系统的频率响应过程与换流器的出力变化。由图7(b)、(c)可知，在下垂控制和所提控制作用下，系统频率最高点明显降低，分别为1.005 6 p.u.与1.004 1 p.u.。由图7(c)可知，所提方法计算出的系统功率盈余与实际值较为接近，所提控制比传统下垂控制具有更快的响应速度，可以在频率事故初期为交流系统提供频率支撑。仿真结果再次验证了所提控制策略可以有效地抑制系统受扰后的频率偏移。

图7 不同控制策略下负荷突减时的系统动态Figure 7 Dynamics of the test system under sudden decrease of load with different control strategies

4.3 IEEE 39系统测试

为了验证本文所提控制策略在不同系统中的适用性，进一步在IEEE 39系统中进行了测试。IEEE 39系统为新英格兰地区高压输电系统等效模型，其详细参数可参见文献[24-25]。如图8所示，测试系统在10号结点处经高压直流输电集中接入了风场发电。类似的，对该处的新能源逆变站分别施加下垂控制与所提的功率附加控制进行仿真分析。

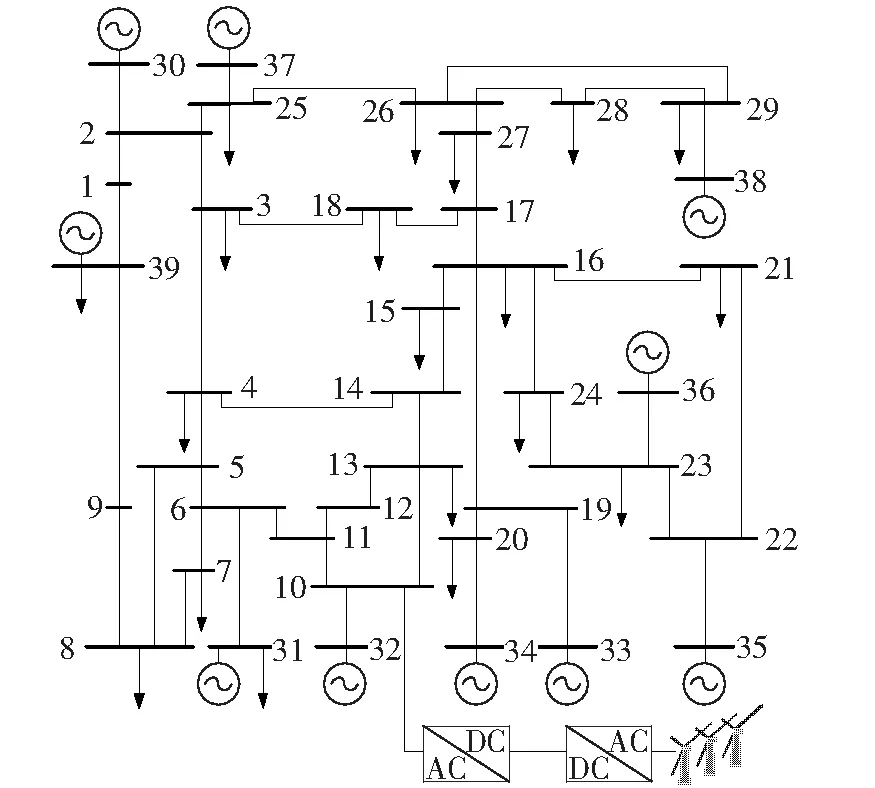
图8 IEEE 39测试系统拓扑Figure 8 Topology of the test IEEE 39 system

系统的动态响应如图9所示。图9(a)为15号结点吸收功率突然增大3.0 p.u.时系统频率的变化过程。由图9(a)可知，本文所提的分段线性近似曲线与系统COI频率曲线十分接近，说明该方法可以由本地测量频率较为准确地估算出系统COI频率。此外，无控制作用和施加下垂控制与本文所提控制策略时，10号节点的最低频率分别为0.996 0、0.996 6、0.997 8 p.u.，验证了所提策略可以快速有效地抑制系统频率下跌。图9(b)为4号节点吸收功率突然减小3.0 p.u.时系统频率的变化过程。无控制作用和施加下垂控制与本文所提控制策略时，10号节点的最高频率分别为1.004 6、1.003 9、1.002 8 p.u.，仿真结果再次验证了本文所提附加功率控制策略的有效性。此外，频率突降与突增情况下，从事故发生到检测出前2个频率二阶导数零点的时间间隔分别为0.347、0.144 s，说明了附加功率控制可以在事故发生后快速启动，及时地为系统提供频率支撑。

图9 不同控制策略下IEEE-39测试系统动态响应Figure 9 Dynamic response of the test IEEE-39 system with different control strategies

5 结语

本文提出了一种适用于高比例新能源电力系统的频率稳定提升控制策略。一方面，根据系统内某一结点频率曲线与系统COI频率曲线的特有关系，提出了基于本地测量的COI频率估算方法；另一方面，根据频率事件后系统的同步惯量与功率变化信息，可以评估系统的等值惯量水平。将两者结合可以在系统动态过程中快速计算系统的不平衡功率，进而利用新能源的快速调节能力为交流系统提供功率支撑。该策略无需通讯设备，实施简单。与传统下垂控制相比，所提策略可以在频率变化初期快速响应，对系统的频率下跌或突增有更好的抑制作用。