基于转子辅助槽的PMSM电磁振动噪声削弱方法研究

贾梦凡, 于 冰, 唐小春, 张殿海

(1.浙江中车尚驰电气有限公司,浙江 海宁 314400;2.湖南省新能源汽车电机工程技术研究中心,湖南 株洲 412001;3.沈阳工业大学 电气工程学院,辽宁 沈阳 110870)

0 引 言

随着国民经济的快速发展，人们对驾乘舒适度的要求越来越高，电动汽车的噪声、振动、舒适感，即NVH性能考核指标日益严格。电动汽车的动力主要来源于电机，而电机性能的优劣直接决定了驾乘的舒适程度[1]。永磁同步电机(PMSM)在电动汽车领域得到广泛应用，随着电机的功率密度和转矩密度不断提高，对新型转子结构要求越来越严格，然而双层磁钢结构具有高凸极比和高弱磁扩速能力，已经成为了主流结构[2]。但是双层拓扑会使电机的转子结构复杂，电机刚度变弱，容易引起振动噪声问题。因此，如何削弱电机电磁振动噪声变得日益重要。

近年来，电机振动噪声问题受到了国内外学者的广泛关注。众所周知，电机气隙中的径向电磁力是引起电机电磁振动噪声的主要原因[3]，对电机的径向电磁力详细分析发现低阶次谐波的影响比高阶次更大[4]。削弱径向电磁力可以通过改变定转子的拓扑结构、增加气隙大小、不同极槽配合等方式来实现[5-7]。齿槽转矩作为电磁振动的次要来源，对电机的空载影响较大，可以通过斜极斜槽、分数槽配合、改变极弧系数、增加辅助槽等方式削弱[8-9]。

考虑定子。李岩等[10]通过解析法和有限元方法分别分析了分数槽配合下定子削齿对电机振动噪声的影响。Zuo等[11]开展了仿真和试验分析，结果表明齿槽效应引起的电磁力对噪声影响最为显著，在对槽口宽进行优化后电磁噪声得以抑制。Torregrossa等[12]通过解析法分析电机的定子槽结构，避免发生共振情况。

考虑转子。国内外学者研究了转子的不同斜极分段对电磁振动噪声的影响[13-15]。王晓远等[16]对电机d轴方向开辅助槽，并对优化前后的电机进行有限元和试验分析，验证了方法的有效性。刘皖秋等[17]提出一种电机转子外表面开辅助槽能够削弱电机的电磁噪声的方法。鲍晓华等[18]通过解析法总结了转子辅助槽对表插式电机转矩脉动的影响。申合彪等[19]分析了不对称磁障对电磁振动噪声的影响。Ishikawa等[20]通过优化电机的转子拓扑结构，降低电机气隙中的径向电磁力，从而抑制电机的电磁振动。

综上所示，为了削弱振动噪声，在d轴方向开辅助槽的研究较多，而在q轴方向开辅助槽的文献相对较少。本文以额定功率为60 kW的电机为研究对象，提出一种转子q轴开辅助槽配合增加气隙宽度的方法来改变电机的磁导，从而降低电机的电磁力，改善声振特性。首先，分析优化前后的两台电机的电磁力理论，对结构模态和A计权声压级进行有限元分析。然后，通过制作样机，对比优化前后的实测噪声结果，证明了仿真结果的准确性，同时证明该方法能够降低电机的电磁力，从而削弱电机的振动噪声。因此，本文提出转子q轴开辅助槽配合增加气隙宽度的局部优化设计方法，能够在低成本的基础上解决实际工程中振动噪声问题。

1 原方案电机测试数据分析

本文研究的电动汽车用PMSM的原方案电机模型如图1所示，其主要参数如表1所示。

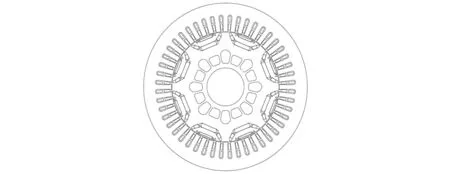
图1 电机原模型截面图

表1 电机基本参数

采用上述方案制作的一台电机进行测试，测试现场图如图2所示。电机在上部(z轴方向)布置一个传声器，后端旋变盖板处布置一个传声器。振动加速度传感器布置在电机机座上下左右四个位置。在500 A(rms)@350 V(DC)的控制器下，对原方案加速峰值工况下的最大输出能力进行分析。峰值电流为480 A(rms)，最大输出328 N·m@130 kW。

图2 样机测试

在加速峰值工况下对电机进行振动和噪声的测试，电机上部传声器采集到的A计权声压级频谱图如图3所示，电机各阶次较明显。

图3 原方案全转速下的A计权声压频谱图

通过图3频谱图所示，48阶次下的噪声相对较为明显，其中对48阶次的噪声声压级在不同转速下进行切片图分析，电机上部传声器采集到48阶次噪声声压级和转速的关系如图4所示。

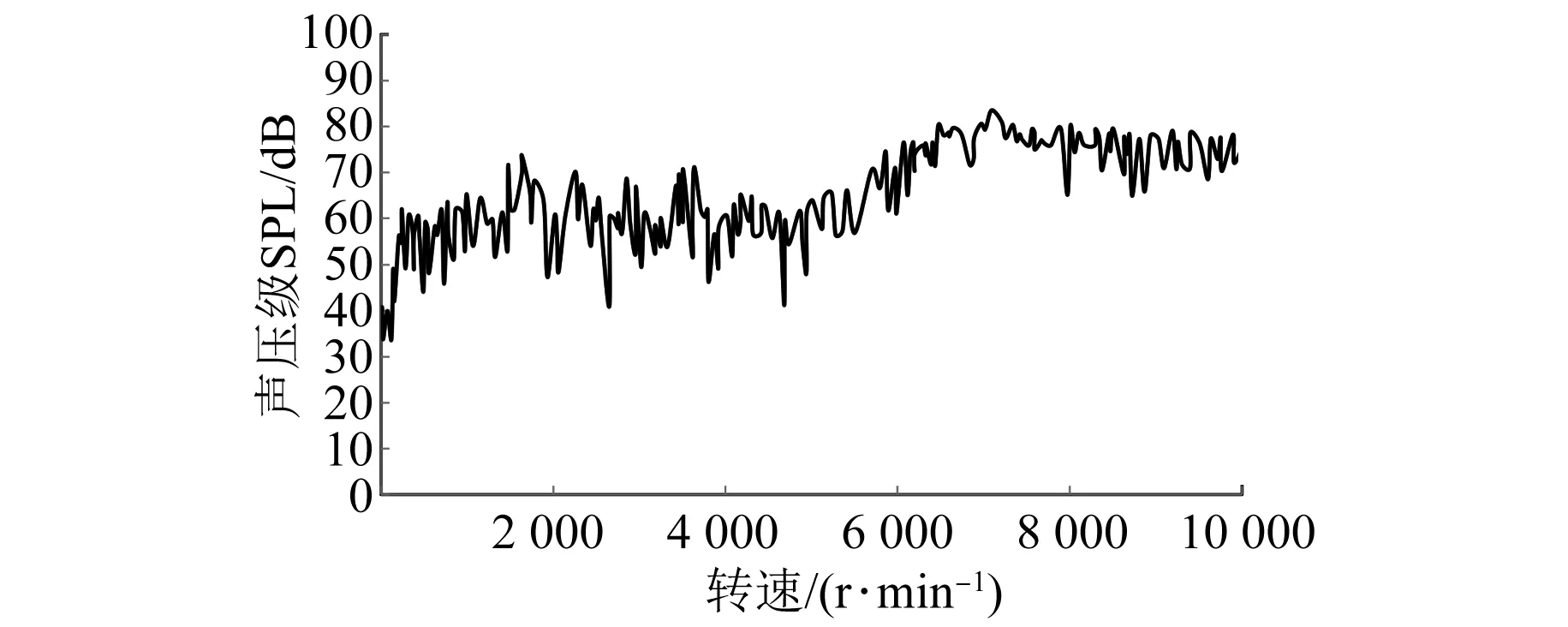
图4 不同转速下原方案48阶次噪声分析

在低速段噪声最高73 dB，噪声值超标，无法满足用车装车需要。在高速阶段无明显啸叫声，在7 000 r/min左右噪声声压级峰值点约83 dB，人耳无明显不适。通过对图4的分析，得出原方案实测数据的主要超标噪声阶次为48阶次，对应的频率如表2所示。低速工况下，整车环境的胎噪和风噪不太明显，驾驶室的主要噪声源来自于电机，随着电机转速不断增加，胎噪和风噪明显增加，因此在高速时，电机本体产生的噪声容易被覆盖。

表2 原方案实测数据超标噪声频率对比

根据对上述实测结果分析，需要对电机的声振特性进行优化设计，重点降低低速段噪声，同步降低高速段噪声。

2 电机电磁力的解析分析

电机的振动噪声主要是由电磁振动引起的，而电机内部的电磁振动主要是由气隙中电磁力作用于定子齿部所产生的，为了解决上述工程问题中遇到的48阶次噪声存在啸叫声的问题，对电机的电磁力数学模型进行分析[21]。

电机气隙中的电磁力是由电机气隙磁密的径向和切向分量产生，铁心材料的相对磁导率远大于气隙，因此与径向气隙磁密相比，切向磁密可以忽略不计，采用麦克斯韦应力张量法，径向电磁力可表示为

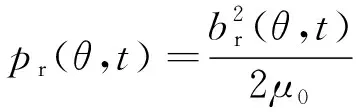
(1)

式中：pr(θ,t)为径向电磁应力;b(θ,t)为气隙磁密;θ为转子机械角度;μ0=4π×10-7H/m。

不考虑电机饱和的情况，气隙磁密可表示为磁动势f(θ,t)与磁导Λ(θ,t)的乘积，即

br(θ,t)=f(θ,t)Λ(θ,t)

(2)

电机气隙磁动势则由永磁体电枢绕组共同产生：

f(θ,t)=fPM(θ,t)+fAM(θ,t)

(3)

永磁体产生的转子磁动势如下所示:

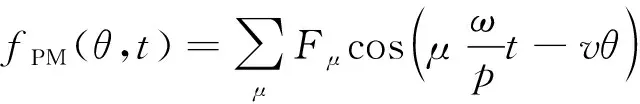
(4)

式中：Fμ为磁动势的μ次谐波幅值；μ为磁动势谐波次数，μ=(2s+1)，s=0,1,2，…；p为极对数。

定子绕组产生的定子磁动势如下所示:

fAM(θ,t)=Fvcos(vθ-ωt-φv)

(5)

式中：Fv为磁动势的v次谐波幅值；φv为v次谐波初相角；v为定子磁势谐波极对数，本文为整数槽绕组v=(6k+1)p，k=0,±1,±2，…。

将式(2)～式(5)代入式(1)，可以得到电磁力的空间力波阶次和时间频率。

当空间阶次为(u-v)，时间阶次f=2sf1。f1为基波频率。

当空间阶次为(u+v)，时间阶次f=2(s+1)f1。

由于空间阶数对定子铁心的变形Δd取决于空间阶数r，两者的关系如下所示：

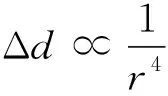
(6)

低周向振型数r(即空间阶数)对于振动噪声行为最关键。如式(6)所示，空间阶数和定子铁心的变形成反比，因此当r≥8时，定子铁心的变形较小，其产生的径向力密度不太重要。如表3所示，通过列力表法分析8极48槽的主要空间阶数和时间谐波频率，表3中仅列出空间阶数≤8，可能出现振动噪声的阶次。

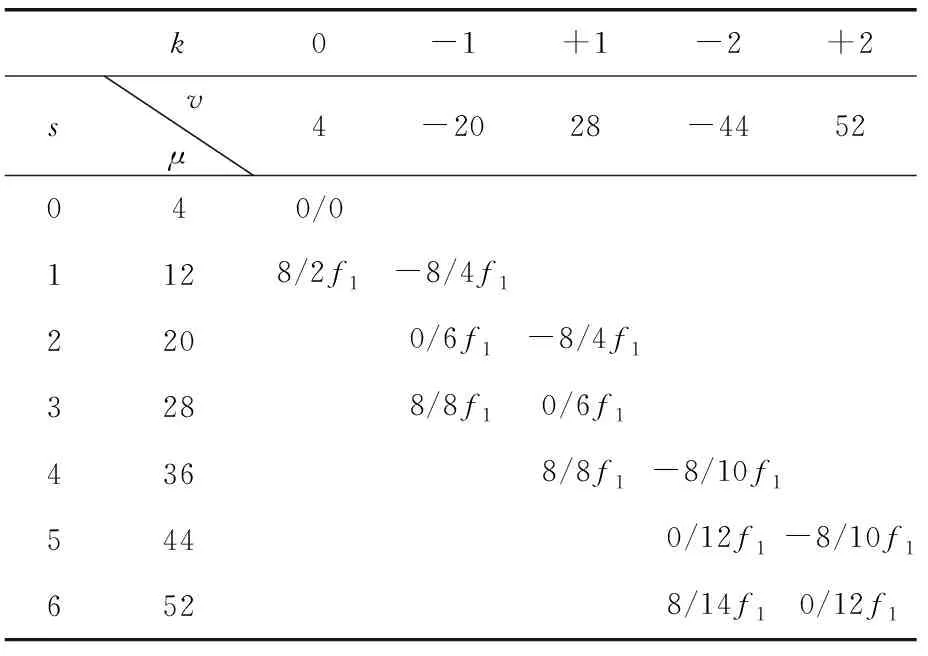
表3 径向电磁力空间阶次和频率

其中，主极磁场u次谐波与一阶磁导齿谐波相互作用是引起同步电机振动噪音的主要根源。齿谐波的极对数为

vi=p±iZ1

(7)

式中：i为齿谐波次数，i=1,2,3，…。

当i=1时，代入式(7)可以得出一阶齿谐波的极对数为52和-44。电机在空载和负载时的电磁噪音主要成分是由一阶齿谐波v=52或v=-44和主极磁场极对数u与定子槽数Z1=48最接近的谐波μ=44、52(Z1=μ时为3个，Z1≠μ时为2个)相互作用所产生的0阶12f1，-8阶10f1，8阶14f1，0阶12f1。

本文的极对数p=4，通过上述电磁力的理论分析，空间0阶的主要电磁力频率为12f1、6f1，分别对应48阶次和24阶次噪声，是噪声的主要来源阶次。第1节中的原方案电机的实测噪声在48阶次出现峰值点，满足上述理论分析的12f1(48阶)易出现噪声情况。通过上述上述理论分析，能够解释在工程问题中的实测结果的有效性。

3 电机的模态分析

对一个电机结构施加一个初始激励后，会产生多种振型，而这些只与结构本身相关的振型称为固有振型。每一个固有振型均对应一个固有频率，空间r阶的固有频率和电磁力的振型、频率一致时候，将会发生共振，对于电动汽车而言，共振存在很大的隐患。李晓华等[22]通过对定子结构系统的固有频率分析，发现在定子铁心的基础上增加绕组对电机固有频率的影响较大。为了能够更加准确地计算电机的固有频率，本文采用有限元方法对电机进行模态分析。电机气隙中的电磁力主要映射定子齿部，通过定子铁心传递，从而产生振动。在尽可能不牺牲精度的前提下，本文仅采用定子和绕组的简化模型进行计算分析。

通过有限元仿真分析能够得到不同空间阶次下，电机定子的固有频率如图5所示。

图5 电机定子模态振型图

通过电机定子模态的有限元分析，可以看出不同振型下对应不同的频率，在空间0阶的固有频率为5 390.1 Hz，实测值在5 200～6 000 Hz频率段内出现峰值点。由于本文未考虑整机数模下的模态仿真，以及在实际运行过程中的复杂性，导致仿真结果和实际可能存在一定的差异性。结合实测结果进行分析，需要重点关注空间0阶的固有频率5 390.1 Hz在6f1和12f1所产生的噪音。

根据工程中原方案暴露的问题，在低速4 000 r/min内，电机未弱磁，电磁力恒定，电机噪声啸叫声明显。而6 500～7 500 r/min中测试噪音有高点。因为电机的噪声响应和电磁力的幅值成正比，所以本文决定通过优化电机转子磁路，降低气隙中的气隙磁密，从而降低电磁力的幅值，削弱电机振动噪声效应。

4 电机优化方案的电磁分析

如式(2)所示，电机的气隙磁密和气隙磁势和气隙磁导相关，不考虑电机定子开槽和转子凸极情况，即气隙长度均匀，气隙磁导用常数Λ0表示：

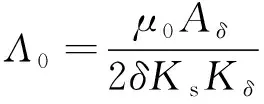
(8)

式中：Aδ为每极气隙有效面积；δ为等效气隙长度；Ks为磁路饱和系数；Kδ为气隙系数。

若仅在定子开槽，相对气隙磁导可以表示为

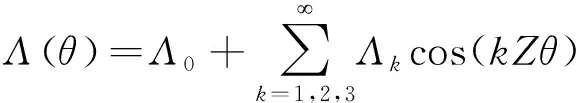
(9)

本文研究的内置式永磁电机，需要考虑由转子凸极引起的气隙磁导变化，转子凸极引起的气隙磁导如下所示：

(10)

如式(8)～式(10)所示，气隙增加会使气隙磁导降低，从而降低气隙磁密和径向电磁力。但是，气隙长度增加会使电机的输出能力降低，而转子开槽会影响转子凸极性，降低电机的电磁力，削弱电机的振动噪声。由于本文原方案实测在低速情况下电机振动噪声整体比较高，因此，适当增加气隙长度配合转子开槽改变电机的凸极性，从而改善振动噪声效应，同时能够在逆变器限制电流下，保证电机具有相同的输出能力。

原方案转子拓扑已经在d轴方向开槽，如果继续在d轴方向开槽，会增加拓扑的复杂程度，导致应力集中，使磁阻增加。因此本文选择在q轴方向开槽，通过优化辅助槽的形状、位置，合理改变磁路的走向，从而降低气隙磁导Λ(θ,t)，由式(2)可知，此方法能够降低电机的气隙磁密，从而能够降低电机的径向电磁力密度，改善电机的振动噪声。通过在原方案转拓扑基础上进行优化设计，以及气隙长度和q轴方向隔磁孔位置的优化分析，以电机输出能力最高和电磁力最低为优化目标，寻求最优参数结果。优化后的电机结构如图6所示，比原方案气隙长度增加0.1 mm，其中在q轴方向增加厚度0.7 mm的辅助槽为最优。图6中，阴影部分为增加的q轴辅助槽位置。

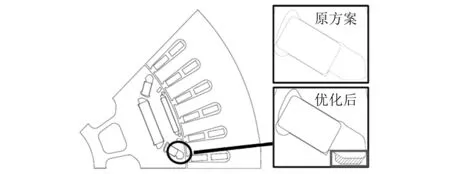
图6 优化后和原方案电机方案对比示意图

为了能够更加清晰地对比由转子开辅助槽配合增加气隙长度使电机磁路发生的变化。原方案和优化后方案的在空载工况下的电机磁力线分布如图7所示。如图7(b)优化后方案所示，由于在转子的q轴区域开辅助槽使得闭合磁力线路径及长度发生变化，如式(8)～式(10)所示，进而会影响电机的磁导，从而影响电机的电磁力。

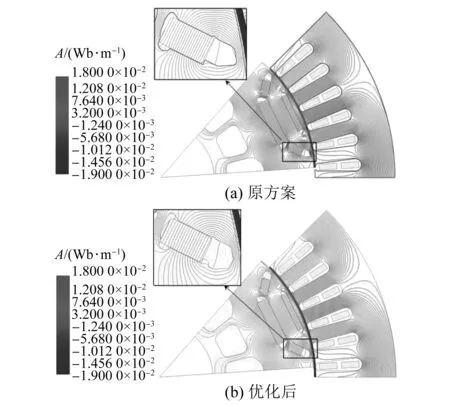
图7 原方案和优化后的空载磁力线分布

由于电机的气隙减少和转子的开槽，可能会造成应力的集中。为了保证优化后的转子冲片高速运行的可靠性，建立3D转子模型，采用有限元方法对电机进行等效应力的计算。为了避免超速的影响，计算转速采用峰值转速的1.2倍，即14 400 r/min。电机的转子材料为硅钢片，屈服强度为405 MPa。计算得到的平均应力分布云图如图8所示，原方案的冲片强度峰值为233.61 MPa，优化后的冲片强度峰值为242.61 MPa左右，均小于材料的屈服强度，能够满足在全转速要求范围内的机械强度。

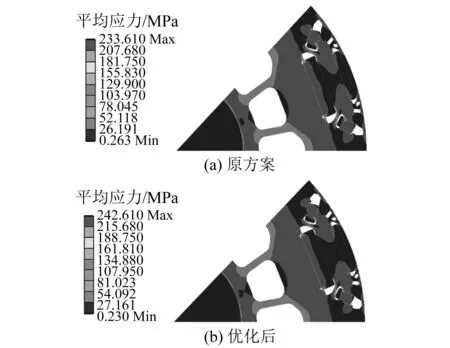
图8 原方案和优化后平均应力分布云图

5 电机电磁力的有限元分析

建立优化前后的电机有限元模型，对优化前后的电机进行全转速仿真对比分析。如图9所示，在峰值480 A(rms)下，原方案最大输出为328 N·m,优化后为323.5 N·m，降低约1.4%，相反高速弱磁区域功率略提升1%～1.3%。总体来看，在500 A(rms)@350 V(DC)控制器下，优化前后输出转矩和功率都满足320 N·m@130 kW的需求。

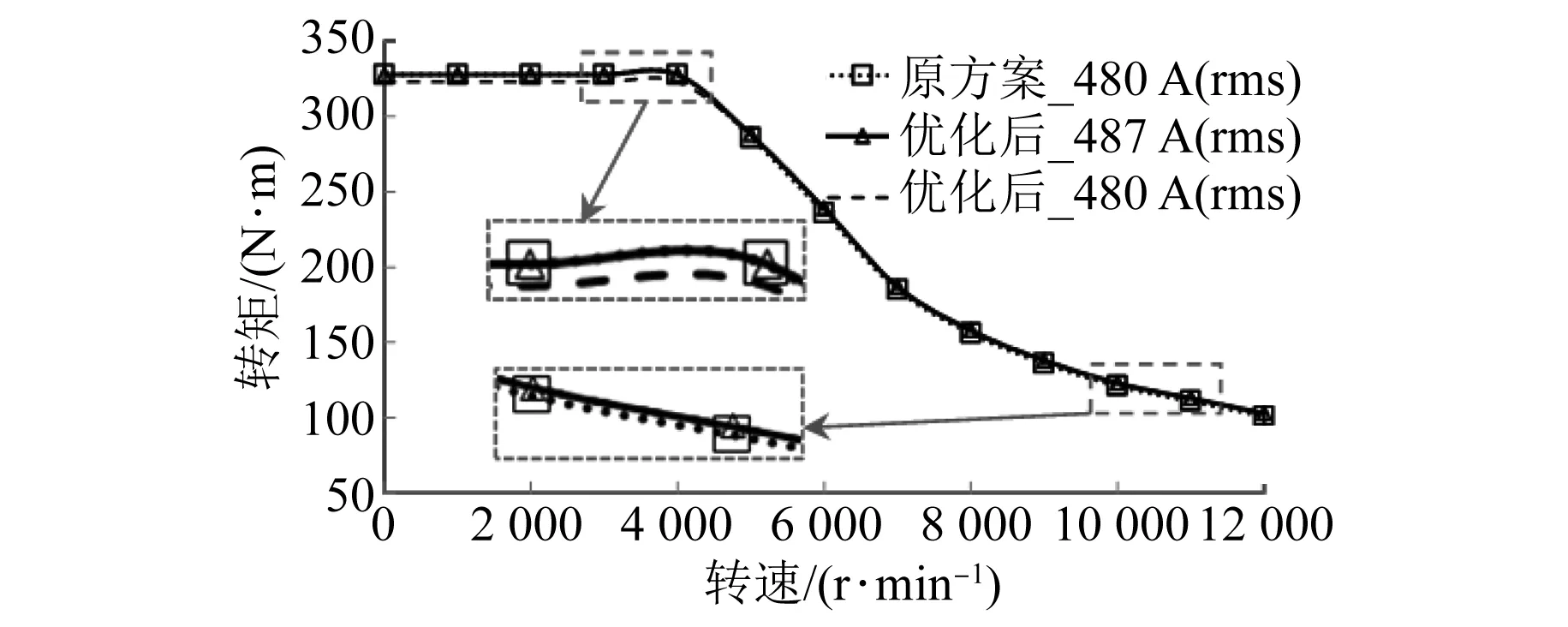
图9 电机的最大输出能力对比分析

但是为了能够对比优化前后电机性能，对优化后同比例提高电流至487 A(rms)，从而保证和优化前的最大输出扭矩一致。因此，下文开展的电机对比均在原方案_480 A(rms)和优化后_487 A(rms)下进行。

电机在实际运行中，转速4 000 r/min以下，整车工况的胎噪和风噪不太明显，驾驶室内主要是电机作为噪声源传递的声音，针对4 000 r/min峰值工作点，本文进行原方案和优化后方案的气隙磁密仿真分析，取靠近定子齿表面的圆孤作为参考点，径向气隙磁密波形及快速傅里叶变换(FFT)如图10所示。

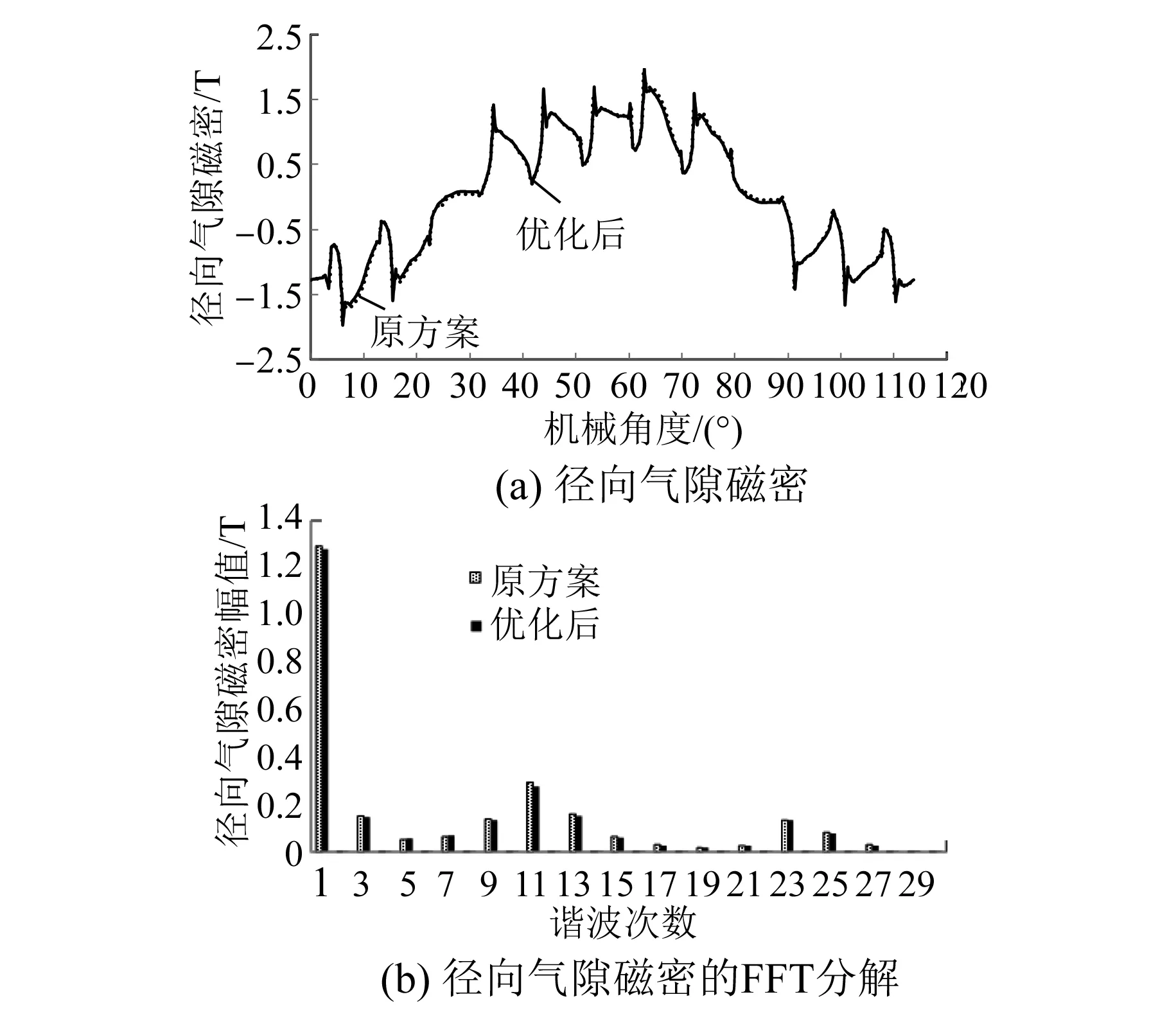
图10 电机的径向气隙磁密和FFT分解

通过图10可以看出，电机的基波幅值几乎不变，对电机的性能影响不大，各阶次幅值均有所降低，比原方案的奇次谐波对基波占比(29次以下)降低约3%，优化后的电机气隙磁密波形正弦度得以改善，证明了优化方案有效。

从电磁力理论分析中可以看出，8极48槽电机的主要频率为6f1，12f1，因此下面主要针对优化前后电机在不同转速下的6f1，12f1的电磁力对比分析，如图11所示。

如图11(a)所示，优化前后6f1电磁力在整个转速范围内均稍有降低，低速降低10.7%左右，高速最高降低23.3%左右。

如图11(b)所示，优化前后48阶电磁力在低速段降低明显，降低49.2%左右，但在7 000 r/min时，超原方案5%；高速阶段最高降低30%左右。

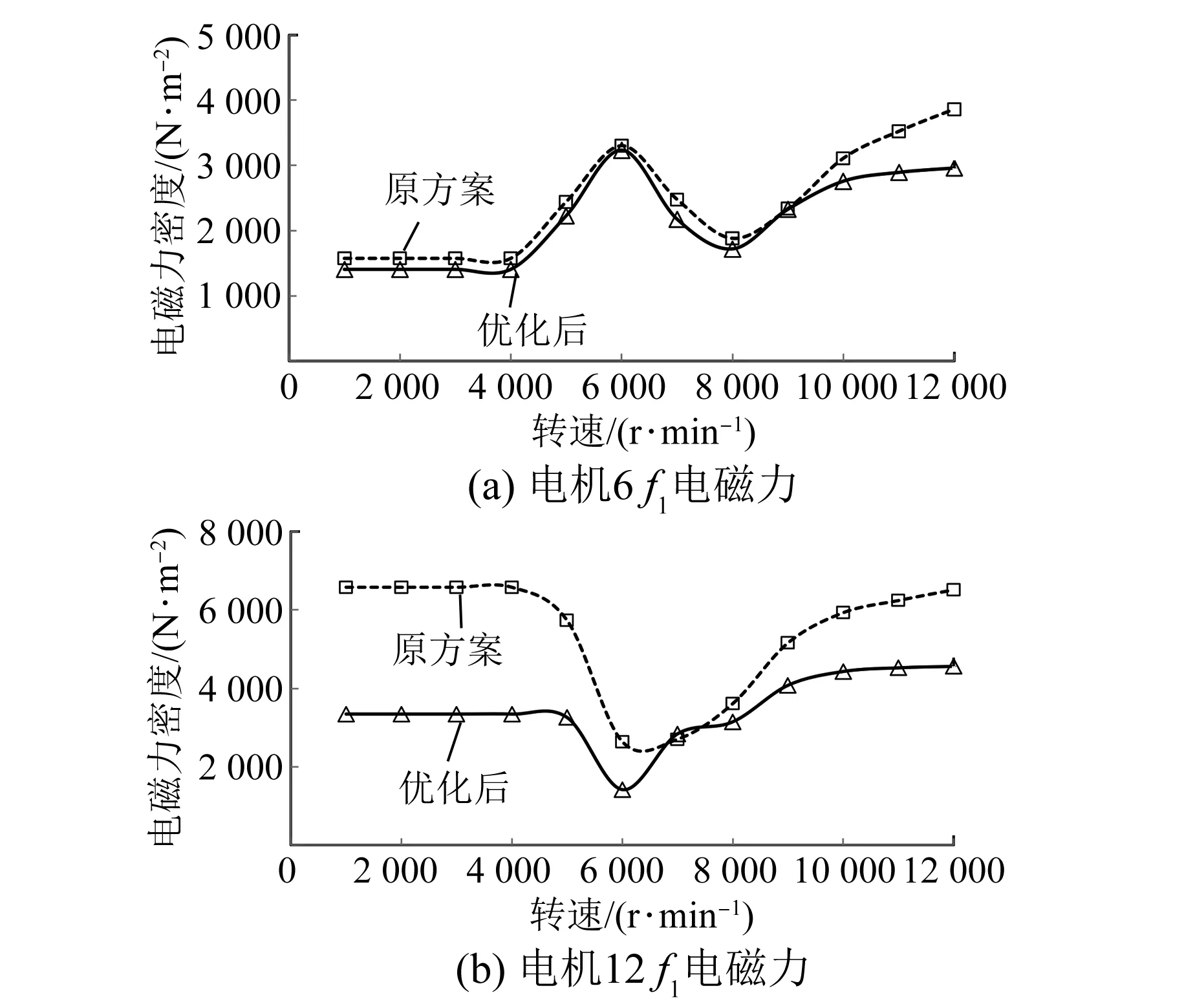
图11 电机6f1和12f1电磁力对比

通过实测和理论分析，电机在低速运行下对整车的影响较大，需要重点降低低速电磁力，同比优化高速电磁力。通过全转速范围6f1，12f1的电磁力分析，优化后方案能够起到削弱电机电磁力作用，满足初始目标要求，证明优化后方案有效。

6 电机的噪声仿真分析

电机定子未发生变化，定子的固有频率和上述分析一致，不再重复分析。保证电机的相同测试环境，在峰值外特性下，计算优化前后电机的全转速工况下的电磁力，然后以集中力的形式加载到定子齿部，电磁力的示意图如图12所示。然后利用模态叠加法计算电机谐响应，仿真结果同步导入到声场计算模块中，进行仿真分析。电机的求解域设置为半径1 m的半球体，重点分析电机侧面产生的噪声分布，分析球体外表面产生的声压级。这也是径向电磁力的主要传播路径。

图12 电机电磁力加载

不同转速下优化前后24阶次和48阶次的A计权声压级仿真结果分析如图13所示。

24阶次声功率等级如图13(a)所示，在电机优化后整个转速区域，A计权声压级都有不同程度的降低，低速降低1 dB左右,高速降低1.5 dB左右。

48阶次A计权声压级如图13(b)所示，在电机优化后整个转速区域，低速和高速降低明显，低速段约降低2.5 dB，高速段约降低2 dB。由于48阶次电磁力在约7 000 r/min时略有增加，使得噪声变化不明显、略有增加趋势。

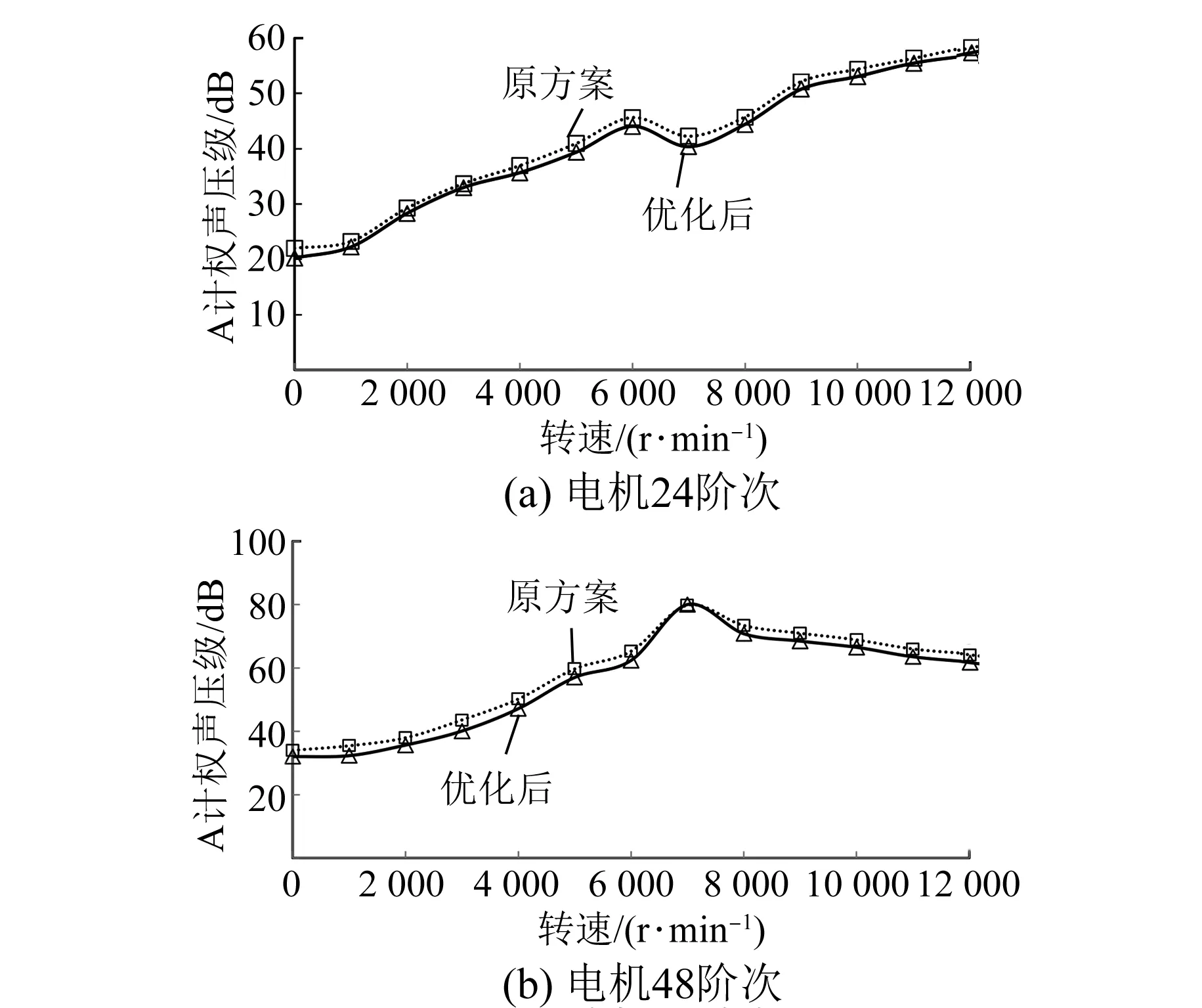
图13 电机24和48阶次A计权声压级对比

从以上有限元仿真结果可以看出，优化后的电机在低速阶段电磁力和A计权声压级的趋势相同，均有降低的趋势，同比高速阶段也有相应的降低，能够证明减少气隙、增加辅助槽的方法的有效性。

7 电机声振特性实测对比分析

为了验证理论和仿真计算的有效性，采用优化后方案制作一台电机对标分析。为了能够区分转子冲片对性能的影响，电机的其余部件均一致。在试验条件下，为了避免电机台架固有频率的影响，采用相同的台架进行测试，振动加速传感器和传声器的布局均和图1相同。在相同的控制方法下，使优化前后电机具有一致的输出能力，对电机进行振动噪声的测试分析。

对峰值工况(320 N·m@130 kW)优化后电机加速分析，上部传声筒采集的频谱图如图14所示，与图3原方案的频谱图相比，各阶次均有一定程度的降低，能够证明仿真方法的有效性。

图14 优化后全转速下的A计权声压频谱图

原方案和优化后方案电机在Z轴方向的48阶振动水平如图15(a)所示，在低速1 800～2 200 r/min区域内，电机的振动水平最大降低约60%，高速区域降低了5%左右。

通过电机噪声近场的采集，在加速工况下，48阶次优化后方案噪声和原方案对比如图15(b)所示。低速阶段，优化后方案整体加速平缓很多，无明显啸叫声，整体波形无明显尖锐点，在低速1 800～4 000 r/min平均噪声声压级降低6 dB,整体降低约10%,高速情况下平均噪声声压级降低3 dB,整体降低约3.7%。

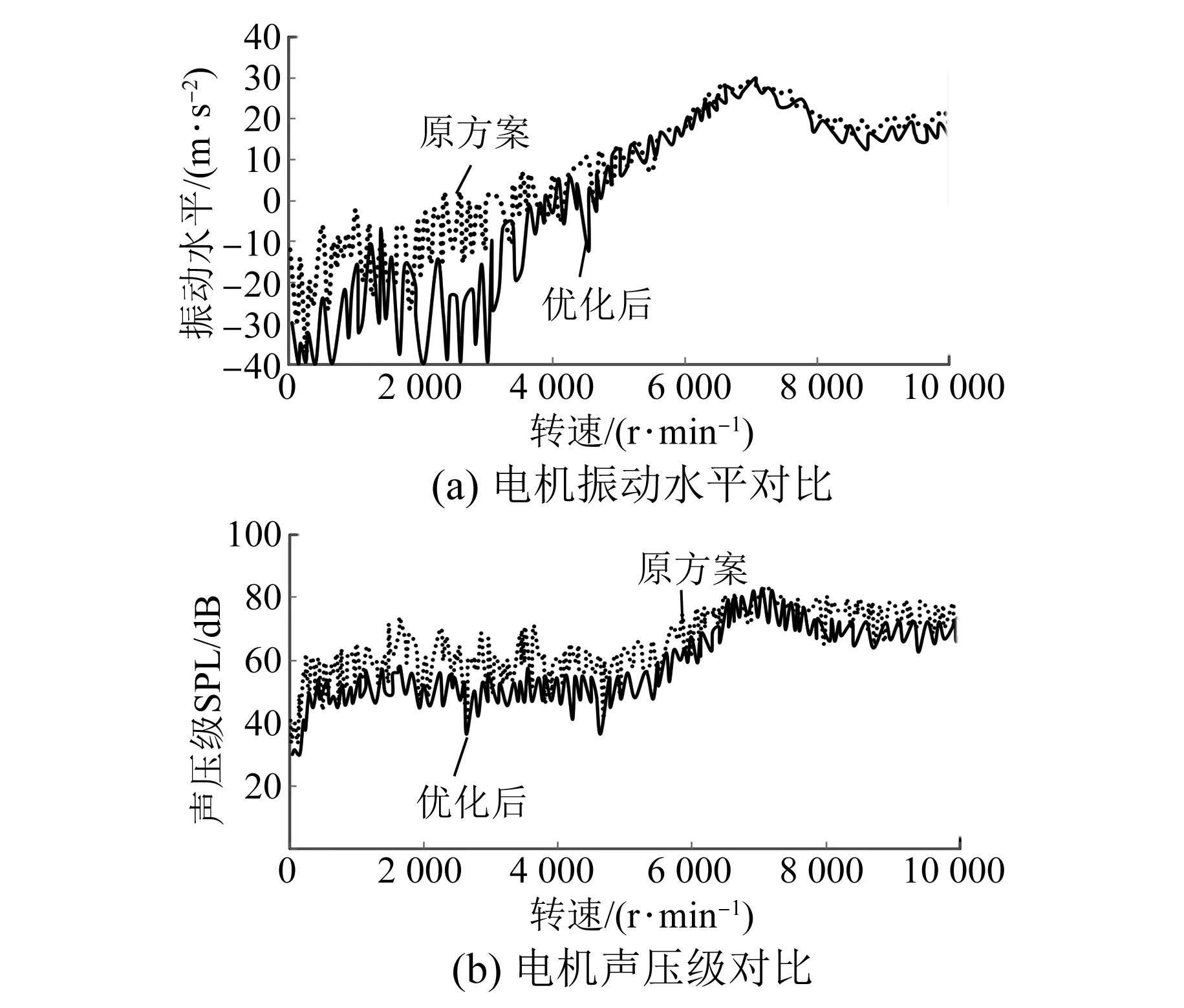
图15 电机的48阶次振动水平和声压级对比

原方案和优化后方案电机在Z轴方向的24阶振动水平如图16(a)所示，在低速区域内，电机的振动水平最大降低约58%，高速区域降低了6%左右。

原方案和优化后方案电机在Z轴采集传声器得到24阶噪声声压级对比如图16(b)所示。低速阶段，原方案24阶噪声无明显尖锐点，优化后方案,低速阶段相比原方案的声压级整体降低约4 dB,降幅6%左右。高速降低约2 dB，降幅2.5%左右。

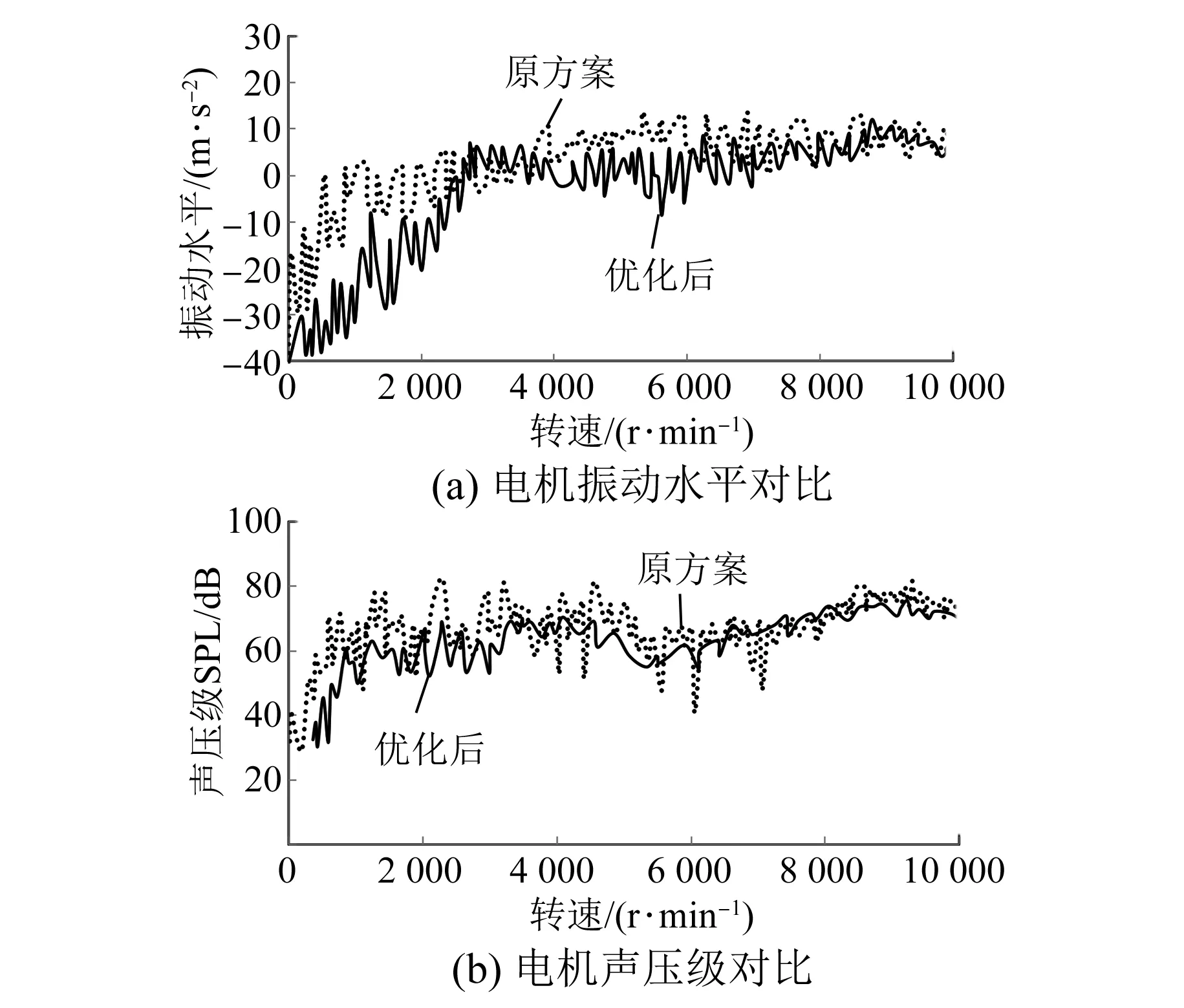
图16 电机的24阶次振动水平和声压级对比

由于仿真结构的模态和实际不尽相同，结果具有一定的差异性，但是通过48阶次和24阶次的振动水平和声压级对比分析可知，在全转速范围内的变化趋势相同；经过实测的验证，可以证明仿真结果的准确性，可以证明转子开辅助槽配合增加气隙的方法具有削弱振动噪声的作用。

8 结 语

本文以一台额定功率为60 kW的电动汽车用PMSM为研究对象，以实际工程中低速48阶次的噪声突出问题为切入点，通过对原方案实测噪声结果进行分析，同时采用解析法进行理论计算验证；然后提出一种转子开辅助槽和增加气隙的方法来削弱振动噪声。对优化前后方案在峰值工况下进行电磁力和谐响应的仿真分析计算，并通过样机试验，测试了全转速下24阶和48阶次的振动和噪声，验证了仿真计算的准确性, 主要得出以下结论。

(1) 本文提出一种转子q轴方向开槽和增加气隙长度的方法降低电机在气隙中的电磁力，从而削弱振动噪声。

(2) 对负载4 000 r/min下对比优化前后的气隙磁密和FFT分析，以及对全转速下6f1和12f1的电磁力对比分析。发现优化后电机的方案能够在低速和高速区降低比例较大，在7 000 r/min变化不明显。

(3) 对全转速范围内的A计权声压级进行仿真分析，为证明仿真的准确性，制作优化后方案的电机，对24和48阶次进行全转速的噪音测试分析，对比声压级和振动水平，能够证明仿真准确性，即能够证明本文提出的转子开辅助槽和减少气隙的方法具有削弱振动噪声的作用。