基于等效磁网络法的混合励磁双定子磁悬浮开关磁阻电机建模研究*
2022-08-09张志友项倩雯孙玉坤
张志友, 项倩雯, 孙玉坤, 袁 野
(江苏大学 电气信息工程学院,江苏 镇江 212013)
0 引 言
开关磁阻电机结构简单坚固、效率高、机械强度大,广泛应用于航天器械、电动汽车、风机、泵等领域。由于临界转速低,摩擦阻力增大,传统的机械轴承限制了开关磁阻电机转速进一步提高[1-3]。磁轴承的出现克服了传统机械轴承的缺陷,开关磁阻电机可以达到很高的运行速度。磁悬浮开关磁阻电机(BSRM)综合了磁轴承技术与开关磁阻电机的优点,无机械磨损、无润滑、能耗低、临界转速高,在飞轮储能、航空航天,涡轮机等领域具有广泛的应用前景[4]。
当前BSRM的建模方法主要有三种:有限元分析法、磁路解析法、等效磁网络法(EMN)。大多数学者对于BSRM的研究基于传统的磁路解析法,应用于电机分析,把磁场问题转化为磁路问题[5]。针对电机出现的磁饱和现象及铁心的非线性问题,该方法分析精度偏低,计算结果可能会和实际误差较大[6-8]。
使用有限元分析软件在电机设计初始阶段需要不断调整参数,因此会造成电机分析设计的时间增长,设计效率低。而且采用有限元软件仿真分析时,需要很精细的网格剖分才可以满足精度要求,单元剖分越精细计算精度就越高,但巨大的网格规模非常占用计算机内存,致使仿真求解过程十分耗时,增加了工程设计的时间和劳动成本[9-10]。
鉴于上述两种方法的不足,利用EMN分析混合励磁双定子BSRM。该方法从磁路法发展而来,同时又采取有限元剖分的思想。采用EMN的仿真时间远低于有限元分析法,此种方法在电机初始设计分析阶段具有良好的应用前景。文献[11]中,英国谢菲尔德大学的Zhu教授将EMN用于对定子永磁型电机的分析,建立磁通切换电机的等效磁网络模型,并基于此模型进一步求解出磁通切换电机的气隙磁密、磁链、电感等特性,通过有限元验证模型的准确性和有效性。文献[12]将EMN用于混合转子永磁电机的设计分析和电机电磁性能评估,进一步研究电机的反电动势、转矩等特性,并与有限元分析进一步比较,证明EMN具有很高的精度。文献[13]提出了一种新的车载双永磁游标电机的EMN模型,将磁路法与网格法相结合,用于预测电机的电磁性能,以提高电机建模效率。并将EMN模型的计算结果与有限元的分析结果对比,验证所建模型的高效性。
本文以24/16/8极混合励磁双定子BSRM为例,提出了一种基于EMN的建模方案。首先采用有限元软件对电机进行磁场仿真分析,定转子齿部和悬浮气隙处磁力线分布均匀且形状类似于矩形,因此可以近似等效成矩形磁导模型求解。定转子轭部可以近似等效成扇形磁导模型求解[14]。转子运动时,转矩气隙不断发生变化,磁场分布较为复杂,采用分割法将外定子与转子间的相对位置分为若干个区间进行研究,对划分的每个区间磁导进行推导计算。根据磁力线的分布确定各个磁导的连接方式,建立起电机的整个等效磁网络模型。对磁网络进行编号,建立起电机的矩阵方程[15]。基于MATLAB软件求解矩阵方程,得到电机转矩与悬浮绕组的电感、磁链等特性,并和有限元分析进行对比验证所建模型的有效性。
1 电机结构与工作机理
1.1 混合励磁双定子BSRM拓扑结构
图1为24/16/8极混合励磁双定子BSRM的拓扑结构图。内外定子和转子铁心材料采用的是DW465-50硅钢片,永磁体材料采用的是钕铁硼NdFe30。电机由24极外定子,16极转子和8极混合内定子构成。混合内定子由8个对称分布的凸极和4个永磁体组成。永磁体采用径向充磁的方式为转子提供偏置磁通,磁极呈NS交替变化,与控制磁通共同形成八极磁场。其他4极与永磁体相间分布。x方向悬浮电流控制x方向的悬浮力,y方向的悬浮电流控制y方向悬浮力。电机外定子等间隔分布24个齿极,其中8个齿极的绕组串联成一相,如图1中的A相所示。定义图1中A相外定子极与转子极对齐时的角度θ=0°。B相和C相分别位于A相顺时针方向的15°和30°处。
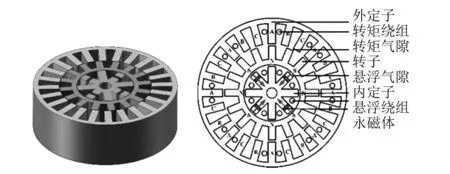
图1 混合励磁双定子BSRM拓扑结构
1.2 工作机理
电机的转矩由外定子与转子作用产生,如图2(a)所示,与传统的开关磁阻电机转矩原理相同,均遵循“磁阻最小原理”。当给转矩绕组通一定大小的电流时,磁通流经转子齿、转子轭、外气隙、定子齿、定子轭部形成闭合的磁路,随着转子的运动,磁场会发生扭曲从而产生切向的磁拉力,产生转矩。
悬浮力由内定子上永磁体和悬浮绕组电流共同作用产生,如图2(b)所示。永磁体产生的磁通Φm流经内定子齿、内定子轭、内气隙、转子轭闭合。悬浮绕组电流产生的磁通Φx流经内定子齿、内定子轭、内气隙、转子轭闭合。当永磁体单独作用时,产生8极对称分布磁通,内气隙磁密相等,此时悬浮力为零,转子处于平衡位置。当x正方向产生扰动时,转子会向x正方向偏移,此时x负方向悬浮气隙减小,磁场变强。给x方向的绕组通电,产生的磁通Φx与Φm在x负方向气隙处方向相反,在x正方向气隙处方向相同,会产生x正方向的悬浮力,使得转子回到平衡位置。
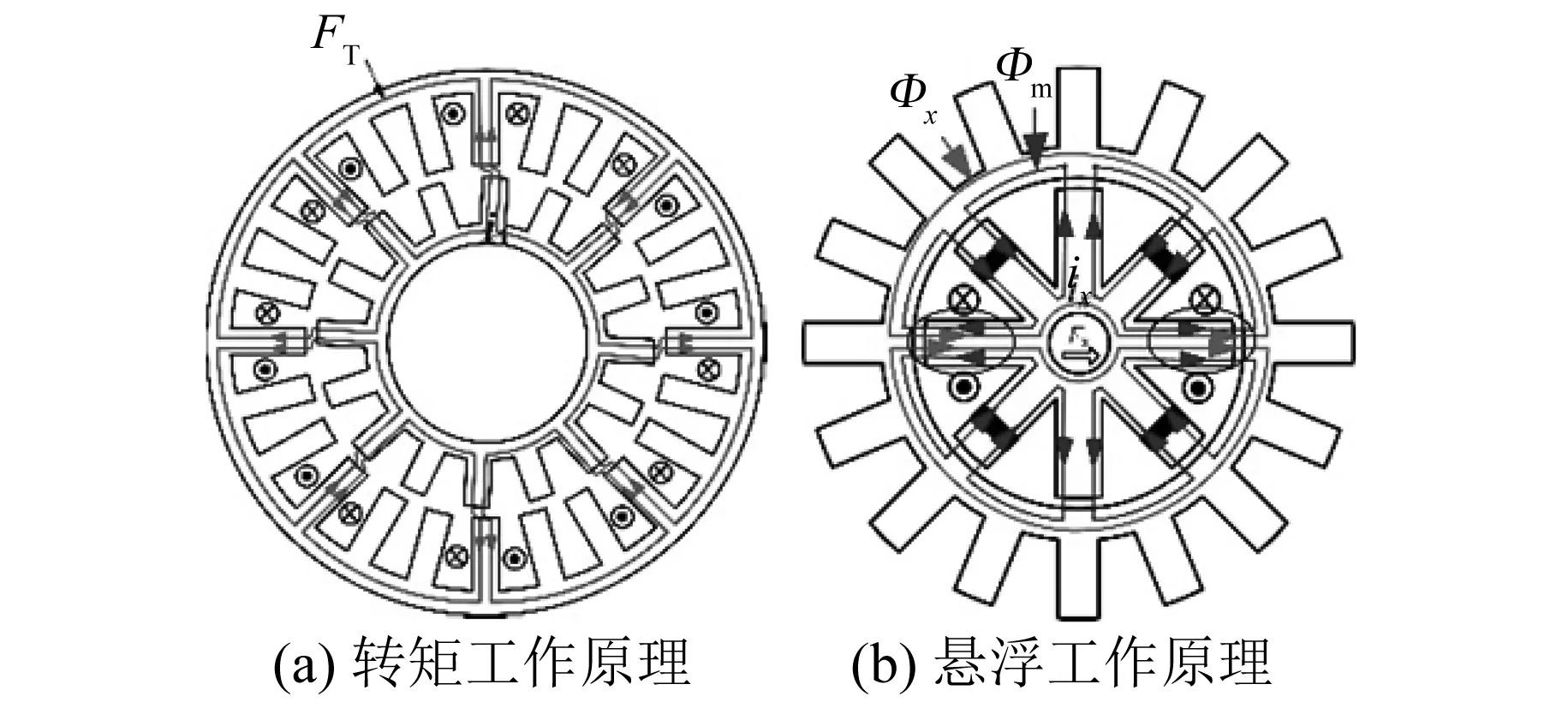
图2 工作机理
1.3 磁路分析
给转矩和悬浮绕组同时通2 A的电流,磁场分布如图3所示。转矩磁场与悬浮磁场彼此独立,实现解耦。转矩磁场8极对称均匀分布。由于ap处偏置磁场与控制磁场方向相同,磁场叠加,而bp处偏置磁场与控制磁场方向相反,磁场削弱,因此ap处磁密较bp处大,在x正方向上会产生径向悬浮力。
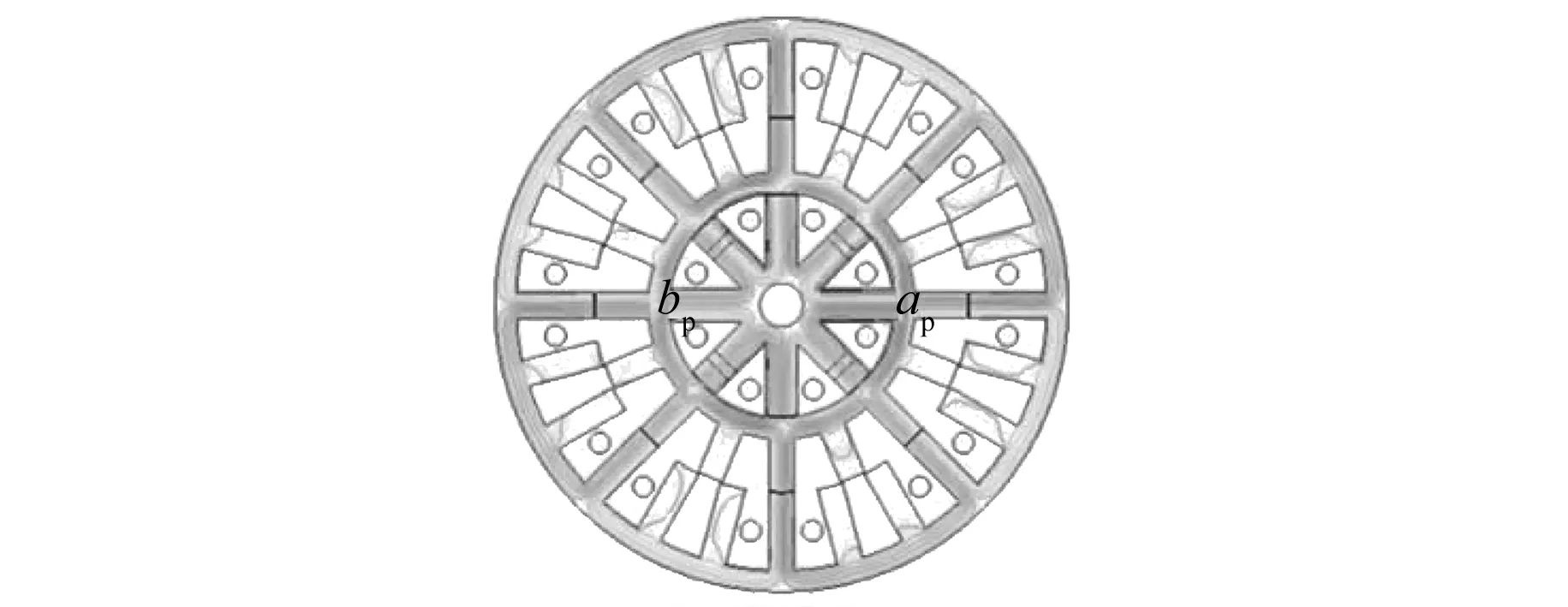
图3 θ=0°磁场分布
2 混合励磁双定子BSRM EMN建模
2.1 等效磁导的分析与计算
2.1.1 定子和转子
考虑到电机定转子结构的特点,可以将电机的齿部和轭部分成两种基本的模型。
图4中,对于齿部而言,内部磁场分布均匀,且类似矩形结构,因此可以直接等效成矩形磁导模型。矩形模型的磁导可以由下式求出:
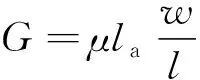
(1)
式中:μ为对应材料的磁导率;la为电机的轴向长度;w为垂直于磁通方向磁截面积的宽度;l为磁通方向长度。
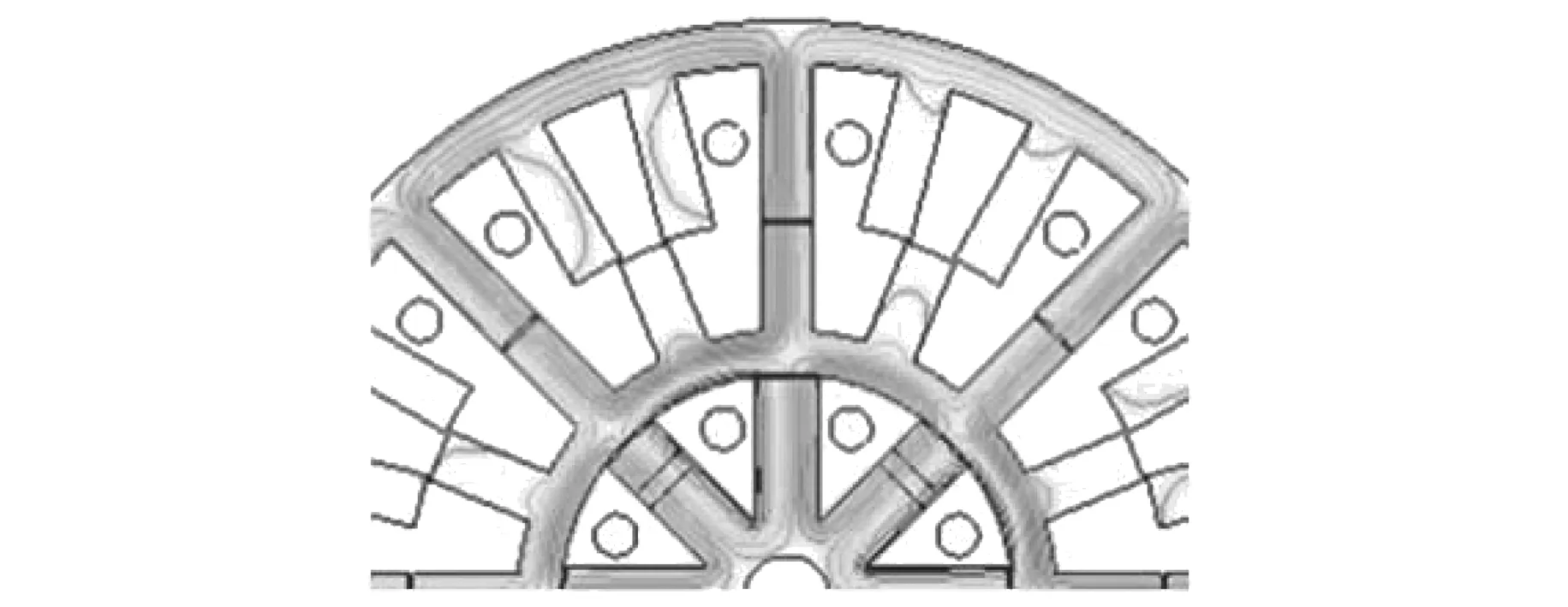
图4 磁力线图
电机的轭部可以等效成扇形模型,如图5所示。扇形模型的磁导可以根据基本的矩形模型进行微积分推导得到:
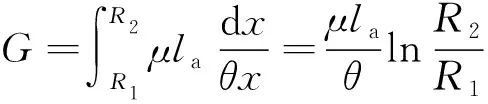
(2)
式中:R1、R2和θ分别为扇形模型的内半径、外半径和开口弧度。
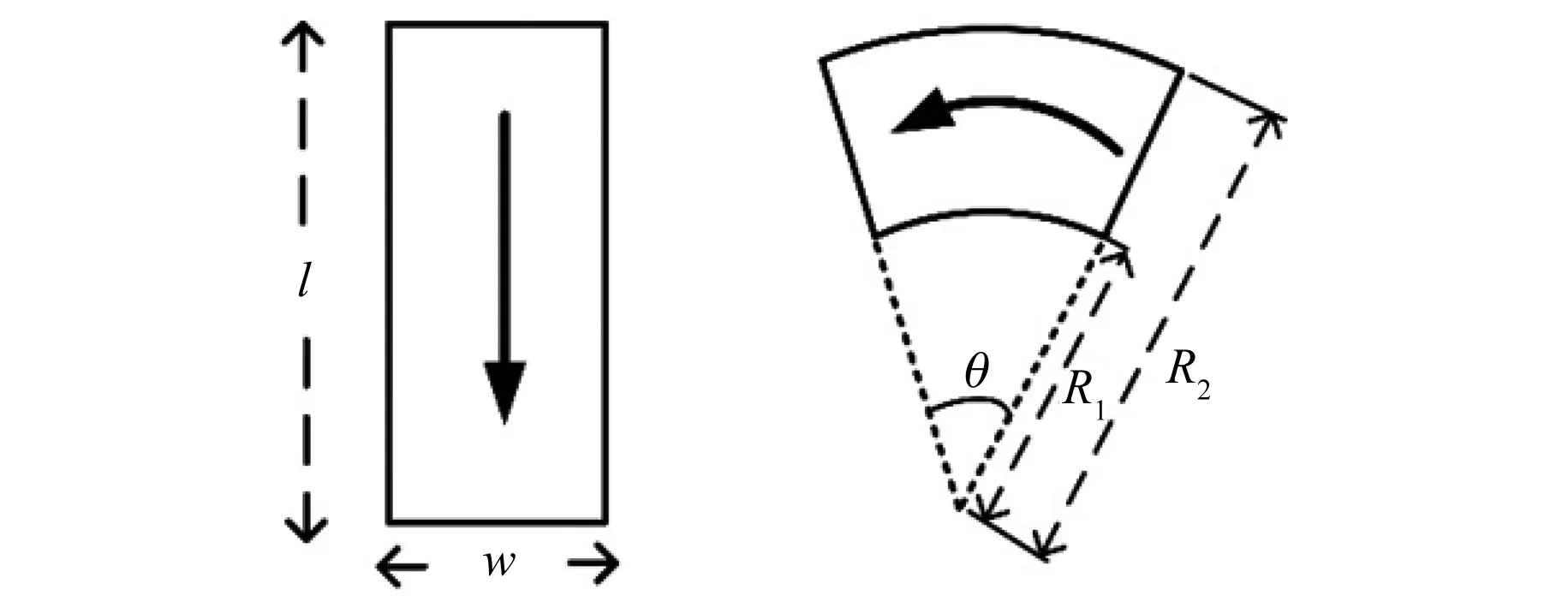
图5 矩形和扇形磁导模型
2.1.2 绕组和永磁体
磁场中的磁动势是由绕组和永磁体产生的,混合励磁双定子BSRM采用的是集中绕组,如图6所示。磁动势的大小为
Fn=∮H·dl=Nci
(3)
式中:H为磁场强度;l为闭环的周长;Nc为电枢绕组匝数;i是绕组中通入电流大小。
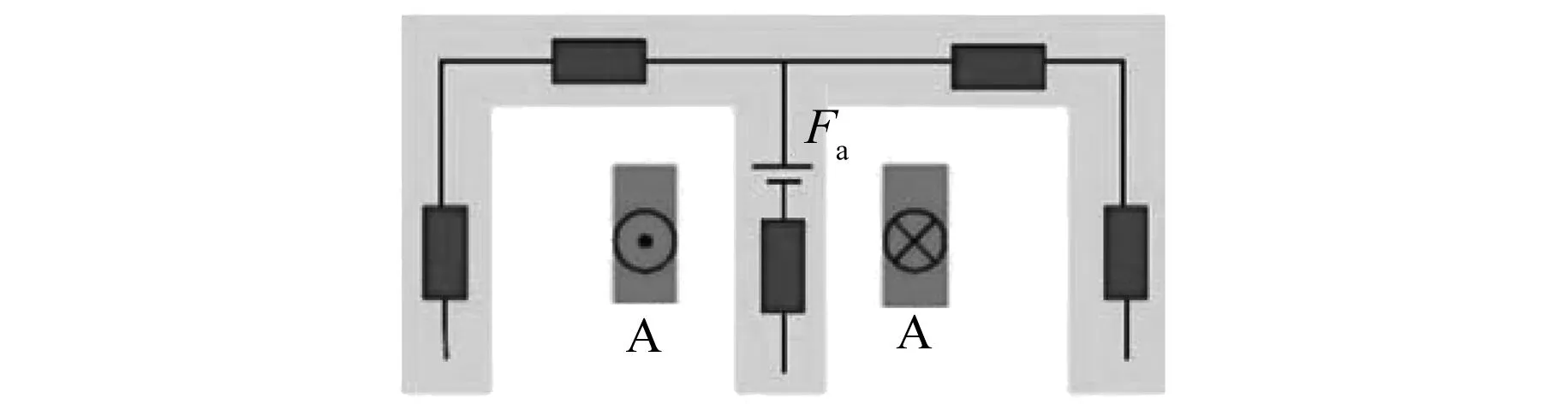
图6 绕组的磁动势等效模型
永磁体等效模型可以表示为磁动势和磁导的串联组合,永磁体的磁动势和磁导的推算公式如下[16]:
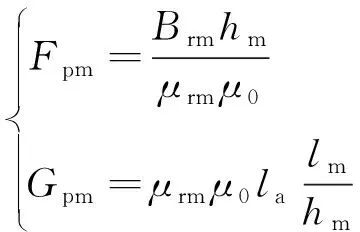
(4)
式中:Fpm、Gpm、μrm、μ0和Brm分别为永磁体的等效磁动势、等效磁导、相对磁导率、真空磁导率和剩磁密度;hm、la和lm分别为永磁体的宽度、电机轴向长度和永磁体的长度。
2.1.3 气隙磁导
在转子运动时,由于内定子磁极与转子间对齐面积始终相等,此部分的悬浮气隙磁力线分布均匀,可以等效成矩形磁导式(1)计算。外定子齿和转子齿之间的转矩气隙可以采用分割法进行研究。
将外定子与转子齿的相对位置分为8个区间进行研究,由α1~α8来定义,即:

(5)
式中:α为外定子齿与转子齿中心线之间的夹角。
图7中是区间1与区间8中外定子齿与转子齿之间的相对位置。α1~α8与电机结构参数有关,例如α1可以由下式定义:
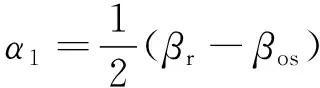
(6)
式中:βr和βos分别为转子和外定子的齿宽。
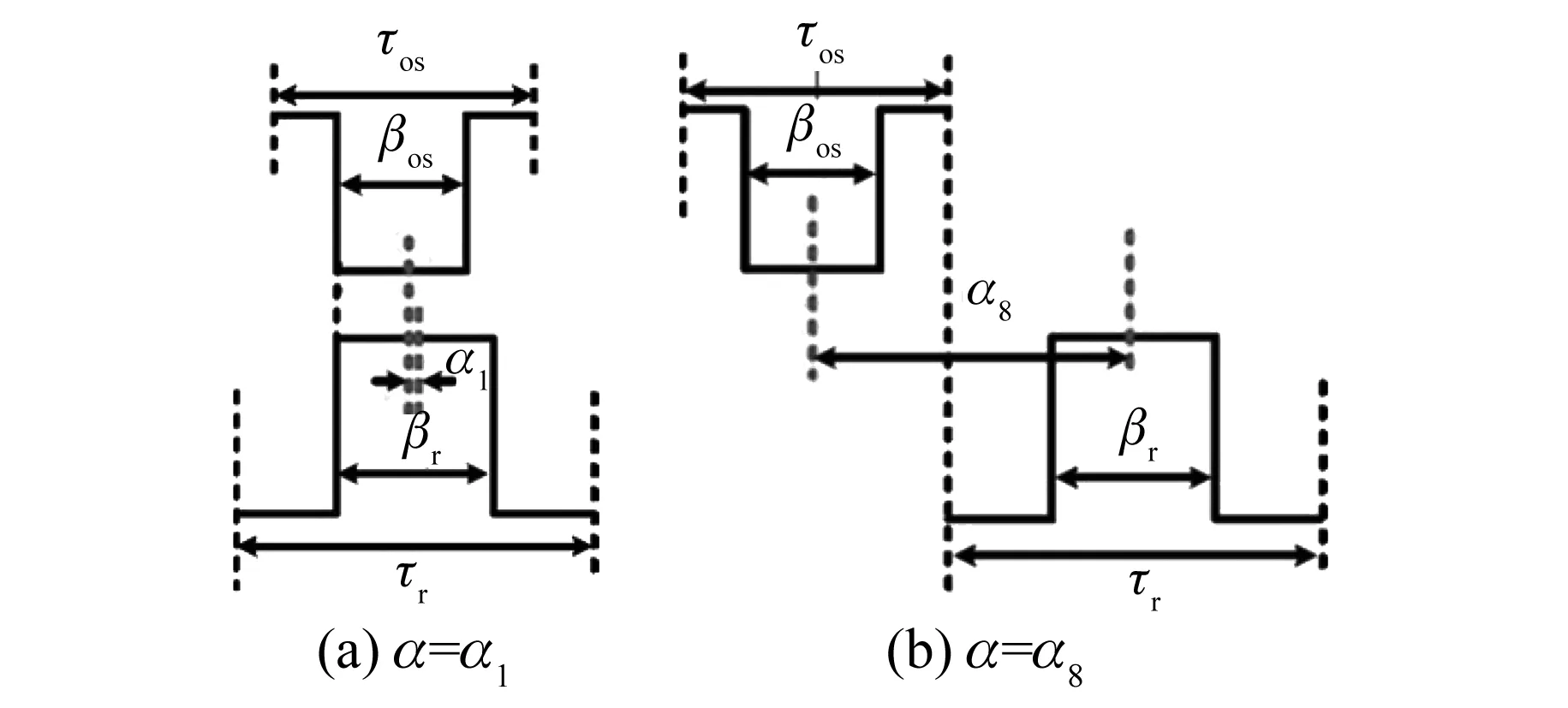
图7 不同区间的转子位置
根据磁通的分布情况,需要将每个区间再分成几个小区间,每个小区间中磁通的分布相对均匀,可以用一个磁导表示。例如,在图8(a)中,区间1就被分成了a~e五个小的区间,每个小区间的宽度如下式:
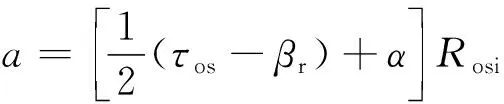
(7)
b=(α1-α)Rosi
(8)
c=βosRosi
(9)
d=(α1+α)Rosi
(10)
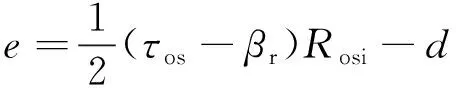
(11)
式中:Rosi为外定子的内半径;τos为外定子齿距,以角速度表示。
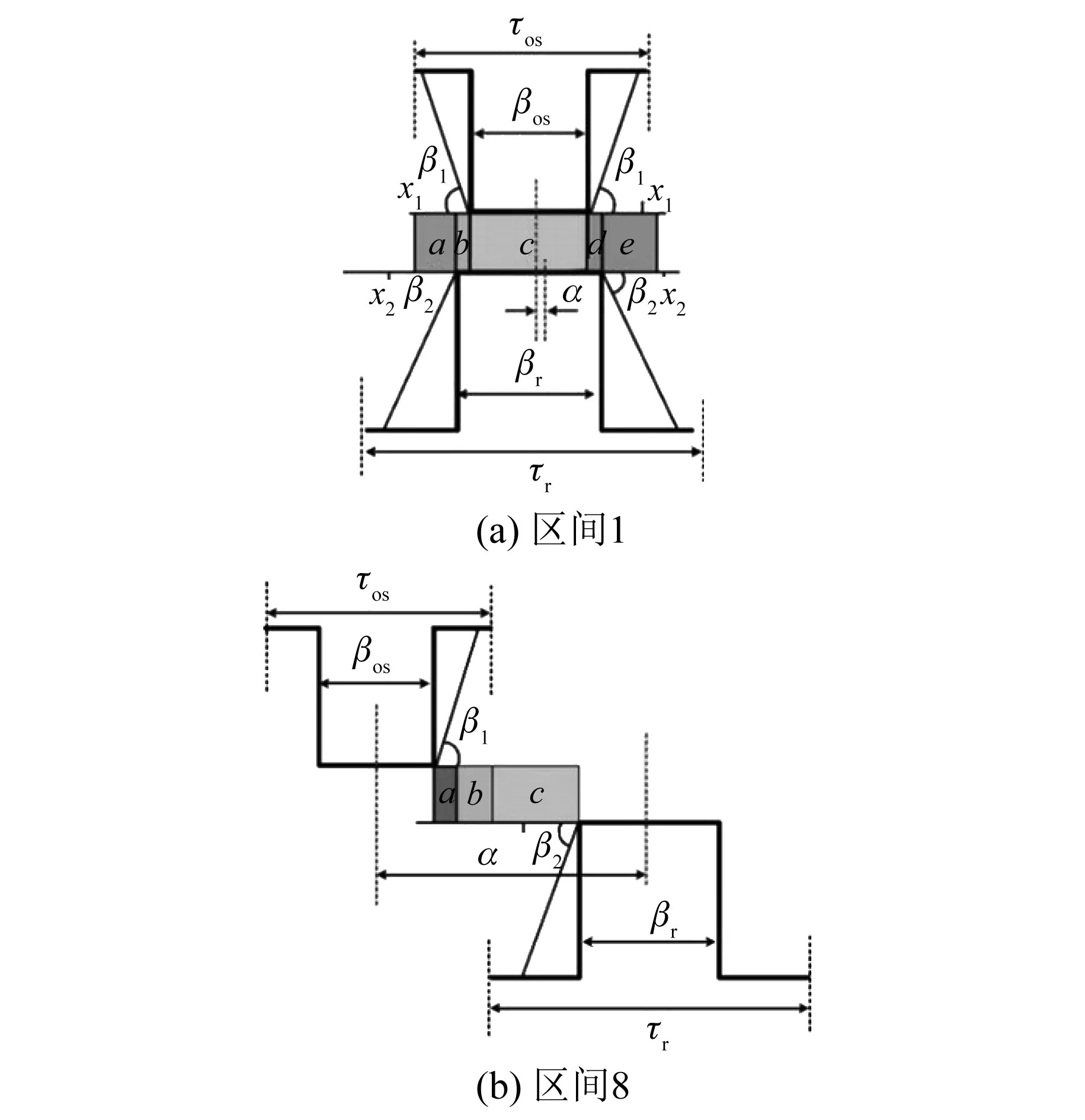
图8 区间分界角的定义
在图8中,将外定子与转子齿的侧面分别倾斜β1、β2角。这么做是为了能够用圆弧和直线代替实际的磁力线。可由下列经验公式确定:

(12)
对应的分界点为:
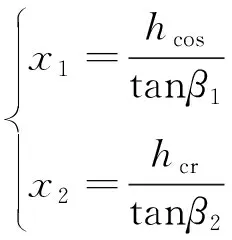
(13)
式中:hcos和hcr分别为外定子和转子磁极高度。
现以区间1为例推算气隙磁导,在子区域a中,磁力线可以看成由两段圆弧和一段矩形组成,其长度随着与转子左边界的距离x而变化。
(1) 由式(1)可以得到子区域a的气隙磁导为
当x2≥a时:
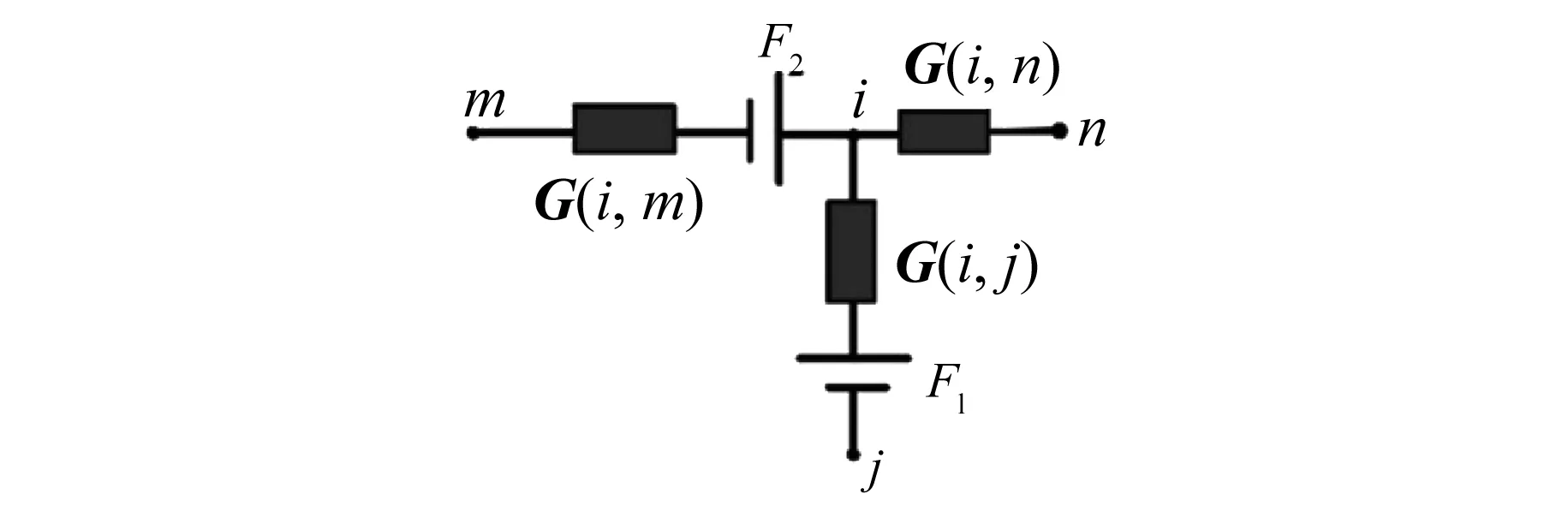
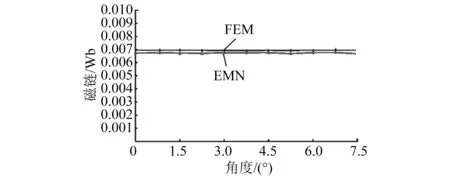
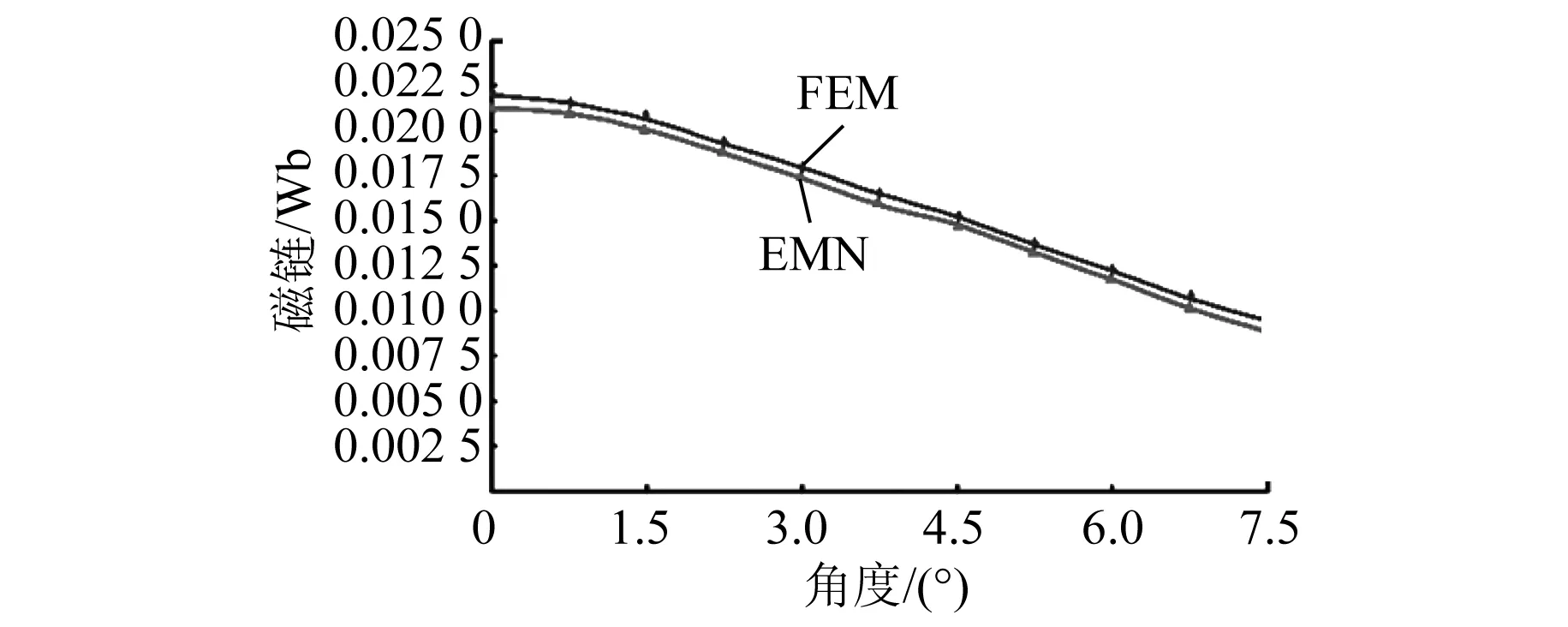
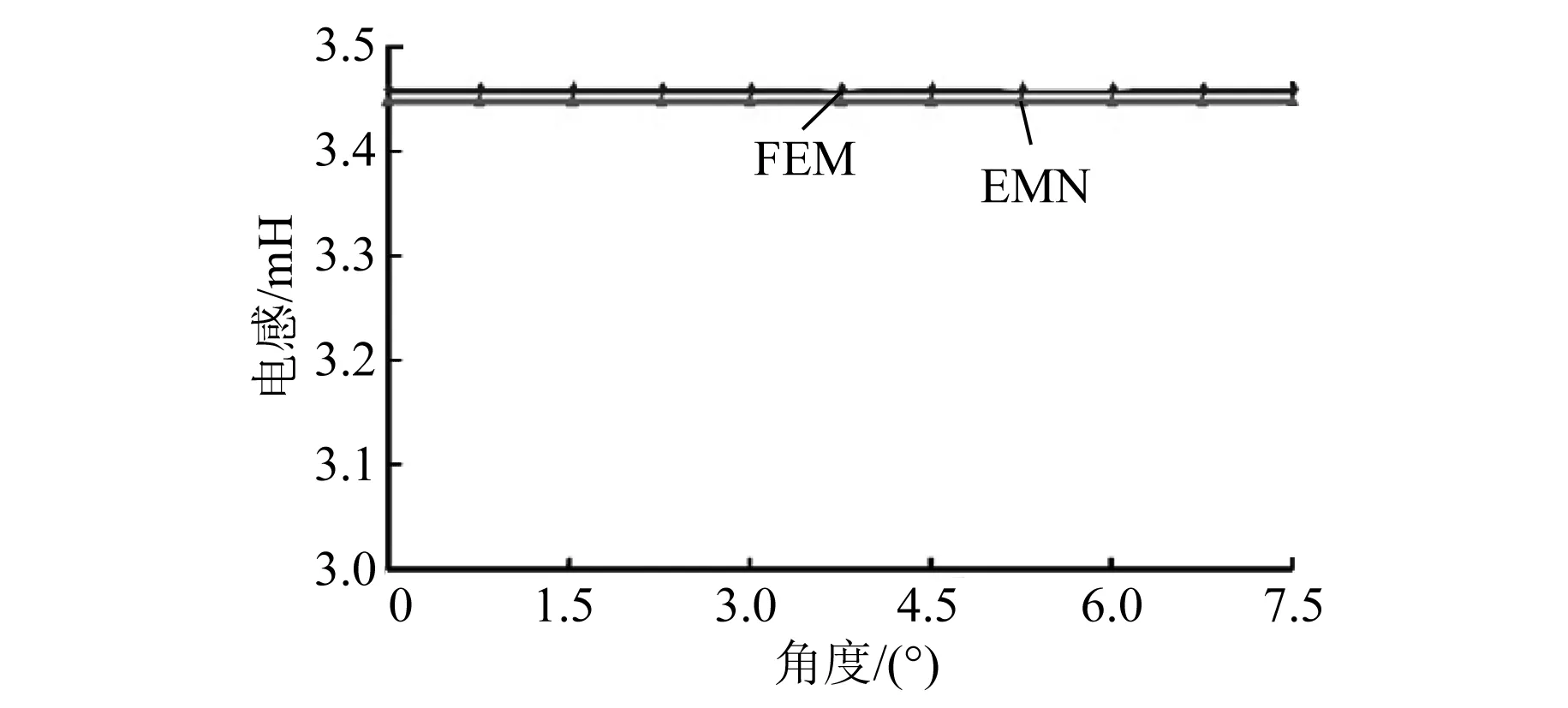
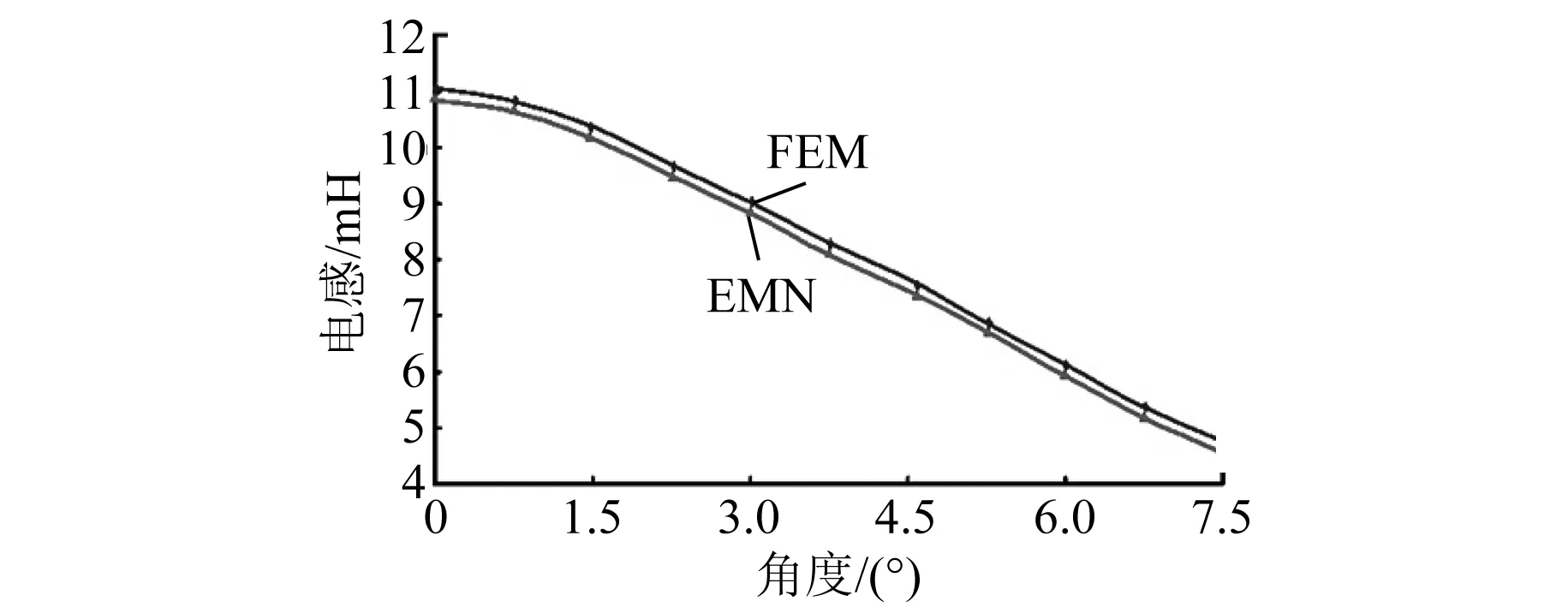
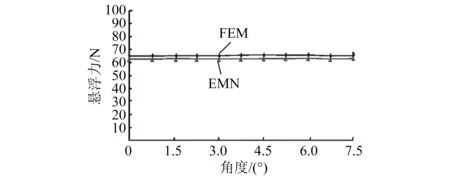
当x2 (2) 子区域b内,磁力线由一段圆弧和一段直线组成,对应的气隙磁导为 (16) (3) 在c区域中: (17) (4) 与子区域b类似,子区域d的磁导为 (18) (5) 在e子区域中,与子区域a类似。 当x2≥e时: 当x2 式中:go为外定子齿部和转子齿部之间的气隙长度;μ0为真空磁导率。 因此利用式(14)~式(20)可以得到区间1总气隙的磁导: Gm=G1+G2+G3+G4+G5 (21) 区间2~区间8的气隙磁导的计算公式可用类似的方法得到。 图9所示为混合励磁双定子BSRM两个特殊位置下EMN模型,表1为电机磁导的种类和编号。 图9 混合励磁双定子BSRM的等效磁网络模型 表1 电机磁导的种类 根据前面求出的所有磁导,结合有限元仿真的磁场分布,确定好磁导的连接方式,磁导矩阵、节点磁动势矩阵和磁通矩阵满足以下关系: G(μi)·Fn=Φn(μi) (22) 根据图9建立的EMN模型,可以观察到节点的总数为92,编号为0~91。 (23) 式中:G(i,j)为节点i和j的磁导;Fn(i)和Φn(i)分别为节点i的磁势和磁通;μi为第i条支路的磁导率。 矩阵G沿着对角线对称,具有如下特点: (24) 如图10所示,节点磁通为已知量,赋值方法如下:若与节点“i”关联的支路存在磁动势,则节点磁通为支路磁动势与磁导乘机的代数和,即 (25) 图10 节点磁通的计算 电机铁心材料的磁导率会随着磁通密度而发生变化,所以铁心材料的实际工作点应该通过一系列的迭代过程得到。采用插值法计算节点i和节点j的磁导率[17]: (26) 式中:Hn和Bn分别为第n个插值点的磁场强度和磁感应强度;Hn+1和Bn+1为第n+1个插值点。 为了提高求解速度,采用超松弛迭代法求解式(23)的矩阵方程,为了得到更好的收敛特性,本文采用定子和转子齿的磁通密度做为收敛判据,其迭代条件可以表示为 (27) 本文以24/16/8极混合励磁双定子BSRM作为研究对象建立起EMN模型。给转子运动设定每个步长,当转动一个步长的时候,就需要重新建立起模型,重新求解建立的非线性矩阵方程。如此就可以求出在单相通电周期(0°~7.5°)时间内,悬浮和转矩绕组的磁链、电感等特性,通过所求的电磁特性结果与有限元法(FEM)进行对比,说明EMN模型的高效性。 假设节点a和节点b是一个磁导的两端,则磁通密度可以由下式求得: (28) 可以进一步求得对应θ位置每相绕组的磁链ψθ: ψθ=NSBθ (29) 式中:N为绕组的匝数;S为齿的截面积,Bθ为θ对应位置下的磁感应强度。 图11和图12所示为给悬浮绕组和转矩绕组通2 A电流时,悬浮和转矩绕组磁链随着转子角度θ的变化情况。从图12中可以看出当θ=0°的时候,即外定子和转子齿极中心轴线对齐时,转矩的磁链值最大。由于内定子齿与转子之间的悬浮气隙在运动的过程中基本不发生变化,这部分的气隙磁导也是固定不变的,求解的悬浮绕组的磁链也基本保持不变。 图11 悬浮绕组磁链 图12 转矩绕组磁链 当求得悬浮和转矩磁链时,可由下列公式求得悬浮和转矩电感L(θ): (30) 图13 悬浮绕组电感 图14 转矩绕组电感 图13和图14表示给悬浮和转矩绕组通2 A电流时,悬浮和转矩绕组电感随着转子角度θ的变化情况。可以看出电感的变化情况与磁链基本一致。EMN模型求解的电感与FEM的电感吻合效果很好。 以x方向为例,x轴正方向为力的正方向,根据麦克斯韦方程可以求出x方向的悬浮力为 (31) 式中:Sxy表示内定子齿部磁极的面积;φx1表示x轴正方向上的磁通;φx2表示x轴负方向上的磁通;μ0表示真空磁导率。 通过对式(31)的求解,可以求出当给悬浮绕组通2 A电流的时候,悬浮力的大小和FEM求解出来的几乎一致,如图15所示。在转子运动的过程中,内定子齿极与转子之间的对齐面积始终保持不变,因此悬浮力几乎保持恒定,不会随θ的变化发生变化,这也进一步确保了转子的稳定悬浮。 图15 x方向悬浮力值 混合励磁双定子BSRM的转矩部分和开关磁阻电机一样,根据能量转换原理,作用在转子上的电磁转矩可以由磁场储能Wa对转子位置角度θr的偏导数得出。所以A相绕组对转子产生的电磁转矩Ta可用下式求出: (32) 当θr=0,即外定子齿和转子齿部正对齐的时候,此时不产生电磁转矩,Ta=0,随着转子的运动,θr逐渐增大,外定子齿与转子齿之间对齐的面积逐渐减少,气隙处的磁力线会发生扭曲,此时电磁转矩逐渐增大。由图16可以看出EMN模型求解出的电磁转矩和FEM求解的基本吻合。 图16 转矩值 本文建立了24/16/8极混合励磁双定子BSRM的EMN模型,推出各部件的磁导公式,尤其是转矩气隙部分采用分割法进行分析。然后对建立的矩阵方程进行求解,进一步可以得到悬浮和转矩绕组的磁链、电感以及悬浮力和转矩特性。通过和FEM分析进行对比,EMN模型求解的结果和FEM求得的结果基本吻合。EMN对于电机的分析具有很好的精度,但用时却远少于FEM。本文分析的EMN可以高效分析BSRM,为此类电机的后续研究提供了一定的参考。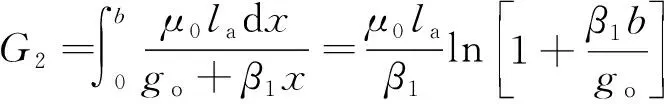
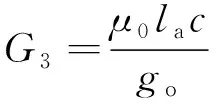
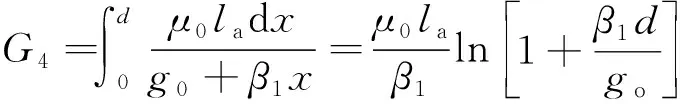
2.2 EMN模型
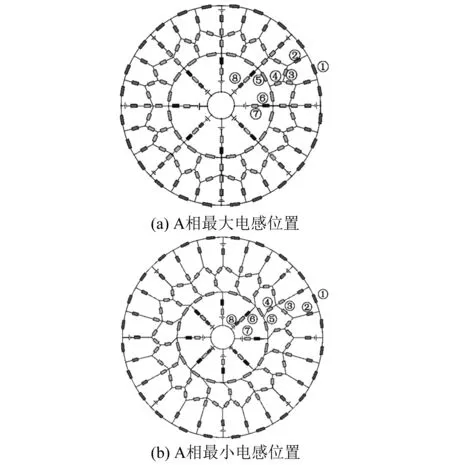

3 EMN模型算法求解

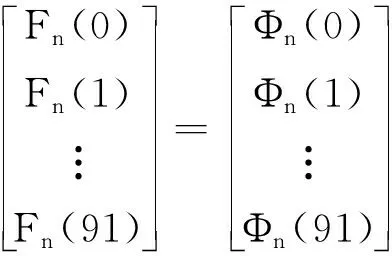
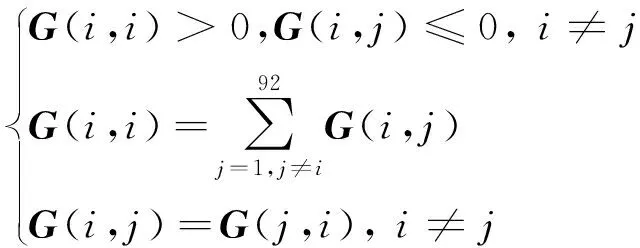
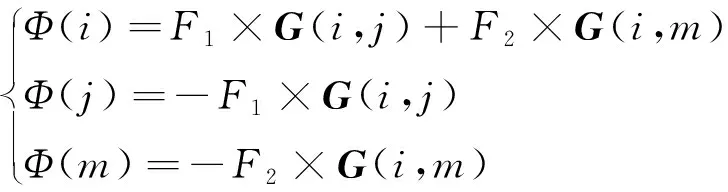
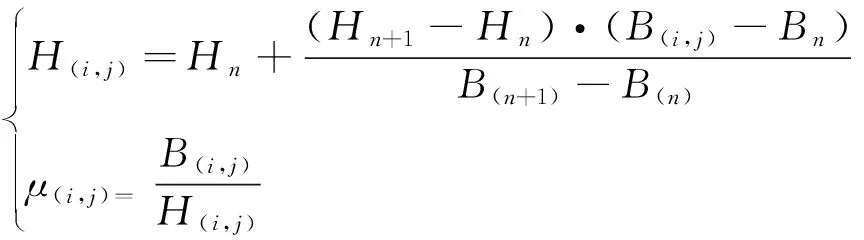

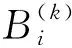
4 结果与验证
4.1 悬浮和转矩绕组磁链
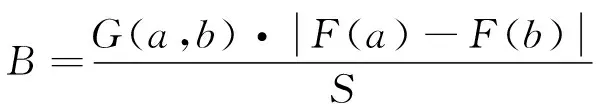
4.2 悬浮和转矩绕组电感
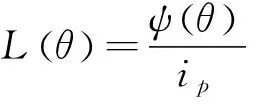
4.3 悬浮力
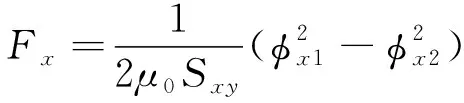
4.4 电磁转矩分析
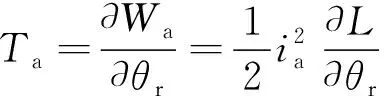

5 结 语
