采用观测气隙的电磁吸力悬浮系统研究*
2022-08-09张晓宇刘国清董金文
张晓宇, 刘国清, 董金文, 吴 桐
(西南交通大学 电气工程学院,四川 成都 610097)
0 引 言
磁悬浮是指通过电磁铁或者永磁体产生的磁场作用到悬浮物体上,使得物体的重力与磁场产生的斥力或者吸力达到平衡,从而实现物体悬浮。随着技术的不断进步,磁悬浮的应用领域不再局限于悬浮列车,在工业生产领域与生命科学领域也得到应用[1]。如磁悬浮轴承[2]、磁悬浮熔炼[3]和磁浮人工心脏泵[4]等。
单自由度悬浮系统有结构简单、数学模型明确、控制性能直观、研发周期短的优点[5]。开环单自由度悬浮系统主要包括电流传感装置、悬浮体、控制电路、电磁铁等。当电磁铁通入电流时,悬浮体会在电磁铁产生的磁场的作用下受到与重力相反的力;不断调节电流的大小,可使悬浮体实现稳定的悬浮。
当悬浮体受到外界扰动时,可能使悬浮体产生过大的位移偏离从而导致电磁力突然变化,失去与重力的平衡,从而不能达到悬浮。为了使悬浮体在外界扰动下仍具有良好的悬浮能力,往往要引入气隙传感器作为反馈从而实现闭环控制[6]。气隙的精确采集对悬浮体稳定悬浮尤为重要,而传统的气隙采集方式对气隙传感器精度的要求高,且造价昂贵、体积大、安装复杂。若采用无气隙传感器的反馈方式,不仅能简化系统、降低成本,同时也能减少由于传感器测量不稳定而导致悬浮控制系统不稳定的风险,从而提高悬浮可靠性。
当前无气隙传感器的悬浮控制研究主要集中在状态估计法和参数辨识法上[7]。状态估计法是选取特定的物理量作为观测量、状态量和控制量。传统的状态估计法选取位置信息、电流大小以及线圈电压分别作为状态量、观测量和控制量。文献[8]引入了状态观测器。考虑到外界对悬浮体的扰动,文献[9]采用了混合状态观测器,这种方法去除了降维电流观测器和外力观测器。文献[10]采用的高频小信号测试法所测量的激励值过大或者过小,容易导致控制效果不精确。
本文以单自由度悬浮系统为研究对象,提出了一种基于磁场和电流观测气隙,使用观测气隙进行闭环反馈的电磁吸力悬浮方法,可实现悬浮控制。分析了气隙与磁场和电流之间的函数关系,对气隙观测函数进行拟合,并分析了气隙函数中的参数对闭环系统稳定性的影响,最终应用观测气隙方法实现了悬浮物在无气隙传感器条件下的悬浮。
1 电磁吸力悬浮系统电磁场悬浮理论分析
在单自由度电磁吸力悬浮系统中,悬浮物分为永磁体与导磁体。本文以后者作为悬浮物,搭建了电磁吸力悬浮模型。
考虑到电磁铁工作时产生的漏磁较大,为单自由度电磁吸力悬浮系统增加了金属外壳以减少漏磁。单自由度电磁吸力悬浮系统模型如图1所示。
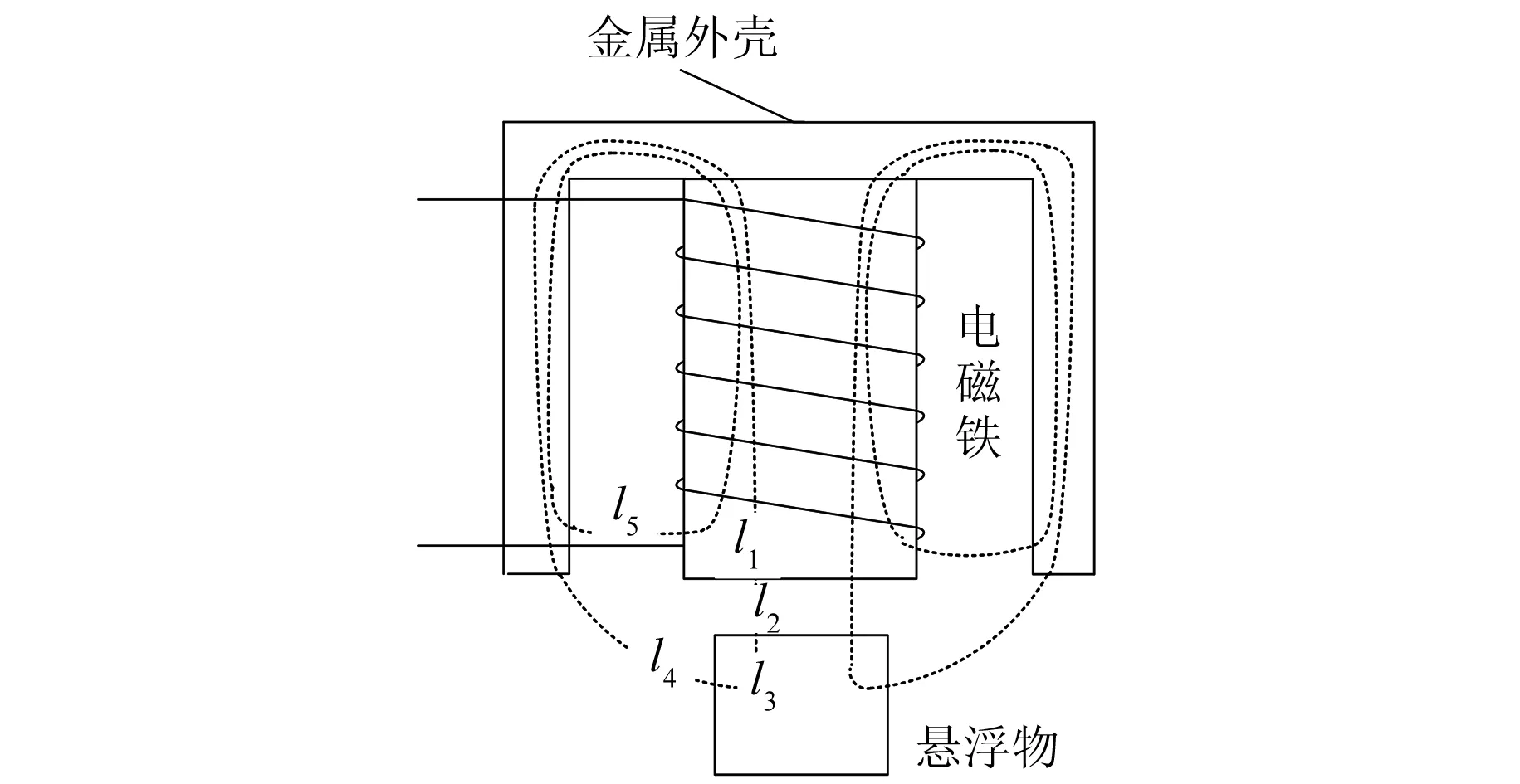
图1 单自由度电磁吸力悬浮系统模型
当电磁铁中通入电流时,根据安培环路定律[11]有
H1l1+H2l2+H3l3+H4l4+Ni′=Ni
(1)
式中:l1~l4分别为电磁铁及外壳、气隙、悬浮物、悬浮物到金属外壳间的积分路径的等效长度;H1~H4分别为电磁铁及外壳、气隙、悬浮物内部、悬浮物到金属外壳间的磁场强度;N为线圈匝数;i′为l5路径上漏磁对应的电流分量。
假设磁场为均匀磁场,则式(1)可以改写为
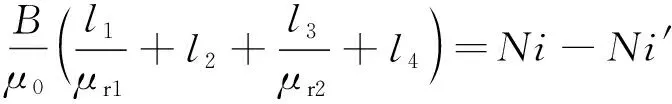
(2)
式中:μr1为电磁铁的相对磁导率;μr2为悬浮物的相对磁导率,μr1=μr2=μr;B为磁感应强度;l2=δ,δ为悬浮气隙值。显然,积分路径l4与气隙存在比例关系。
式(2)可以表示为
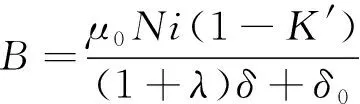
(3)
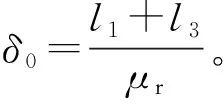
由于结构原因,会有一部分磁通只经过金属外壳而不经过悬浮物。假设这部分漏磁Ni′不会随气隙变化而变化,而与流经电磁铁中的电流正相关,则式(3)可写为

(4)
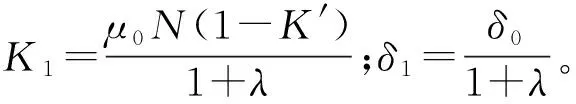
2 电磁场有限元仿真
为了验证对式(4)假设的正确性,选取7 mm作为悬浮平衡点,对不同电流下的电磁模型进行有限元仿真。仿真参数如表1所示。仿真结果如表2所示。

表1 电磁铁仿真参数

表2 仿真结果
由表2可知,漏磁大小与气隙近似无关,与总安匝数近似成正比。
为了获取更准确的磁场,设计了两个磁场测量点,如图2所示。位置1是悬浮物顶部几何中心,位置2是电磁铁底部几何中心。仿真参数仍如表1所示。
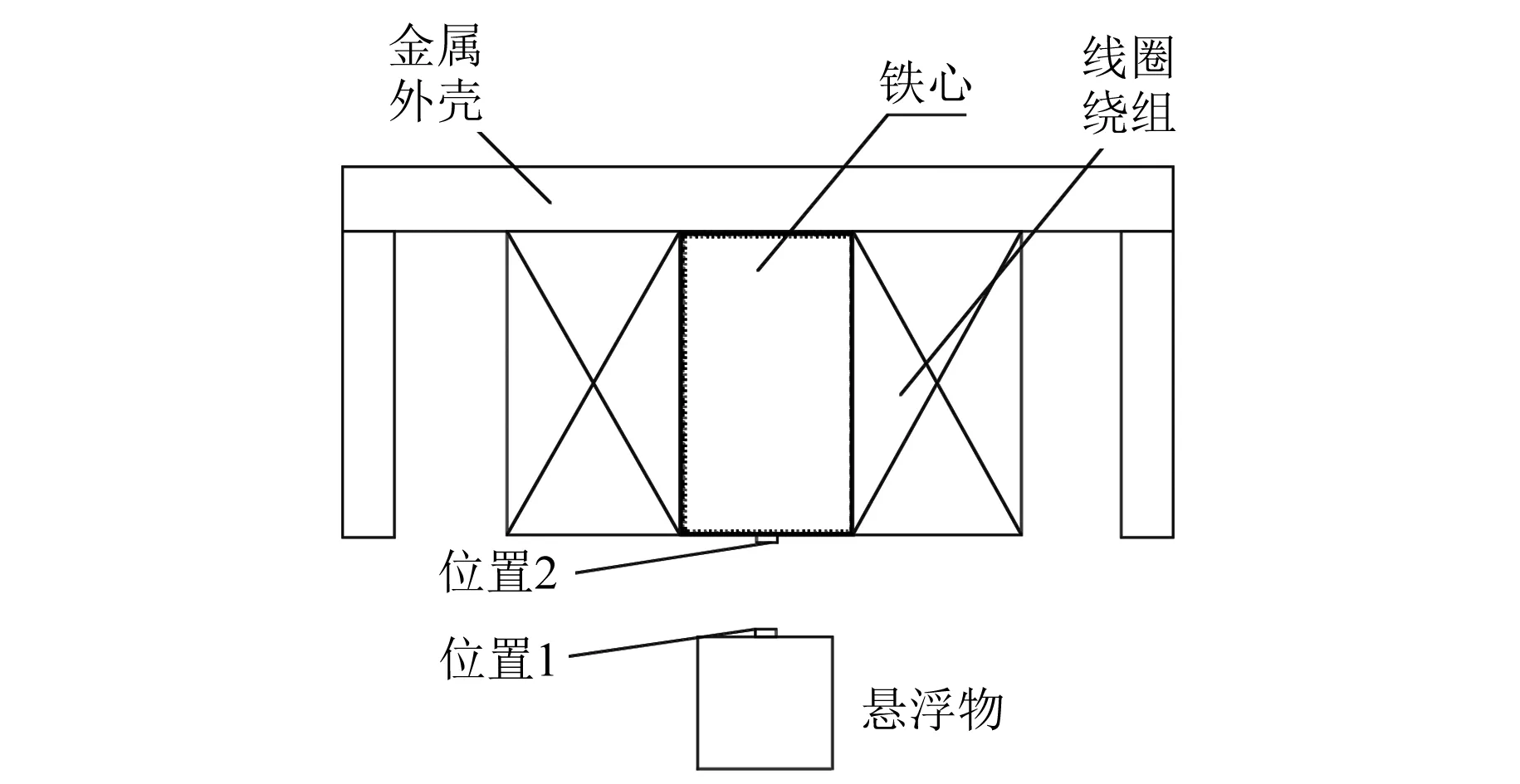
图2 霍尔传感器不同放置位置
气隙为7 mm,电流为2.5 A时,磁密分布图如图3所示。

图3 磁密分布图
磁密分布图显示,气隙为7 mm时,气隙的磁感应强度仅为0.07 T左右,未达到悬浮物磁场强度的饱和值0.84 T,可以认为此时磁感应强度与磁场强度之间的关系为线性关系。
分别对位置1与位置2两个位置的磁感应强度随气隙的变化情况进行仿真。结果如图4所示。

图4 位置1、2磁感应强度值
大气隙下漏磁不断增多,导致位置1较位置2磁感应强度值变化更明显。
3 磁场测量及传感器安装
由式(4)知,若K1已知,则可以借助通入电磁铁中的电流和磁感应强度观测气隙,磁感应强度可以通过霍尔传感器测量。与气隙传感器相比,霍尔传感器安装方便,成本低,更易于集成,可以通过磁场测量电路输出一个电压信号。磁场测量原理如图5所示。
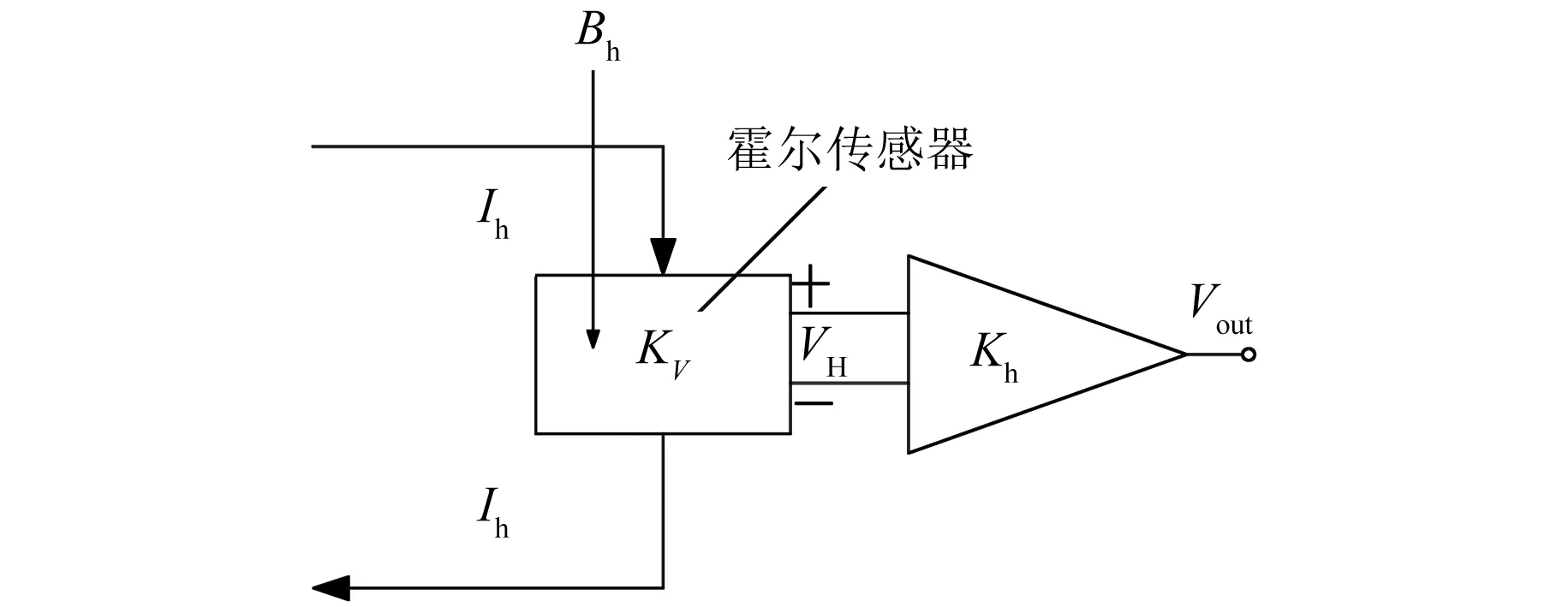
图5 磁场测量原理
当通入霍尔传感器中的电流Ih与通过霍尔传感器的磁场感应强度Bh恒定时,霍尔传感器两端的电压与温度的关系为
VH=KT·T+a
(5)
式中:VH为霍尔传感器两端电压;KT为温度系数;KV为霍尔传感器敏感系数;T为温度;a为偏置。
磁场测量电路输出的电压与霍尔传感器两端电压关系为
Vout=KhVH=KhKVIhBh+aKh
(6)
式中:Vout为磁场测量电路输出的电压值;Kh为磁场测量电路的放大系数。
在电磁铁中通入2.5 A电流,测得在气隙为7 mm时两位置磁场测量电路输出电压变化情况如图6所示。
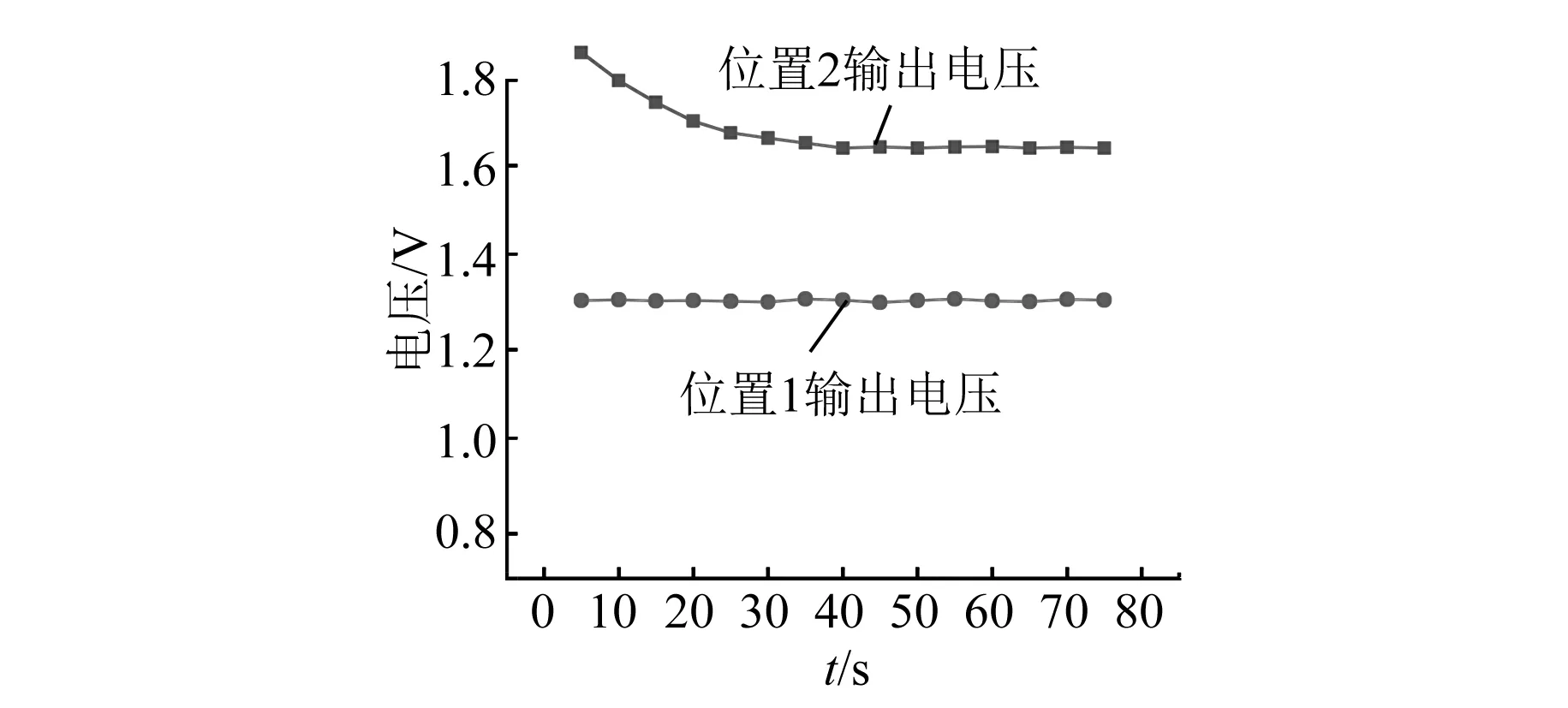
图6 相同电磁铁电流下位置1与位置2的磁场测量电路输出电压
由图6可知,当霍尔传感器放在位置2时,随着时间增加,磁场测量电路的输出电压先逐渐减小然后保持不变,这是由电磁铁通入的电流导致电磁铁温度升高所致。当霍尔传感器放在位置1时,输出电压基本保持不变。
综上所述,位置1对磁感应强度的灵敏度高于位置2,且位置2易受到温度影响,故将霍尔传感器放置于位置1。

图7 位置1的磁感应强度
将霍尔传感器置于位置1,在线圈中通入2.5 A的电流。由表2知,可以近似认为在平衡点附近固定漏磁为总磁通的40%。计算式(4)中λ为0时的磁感应强度的理论值并对电磁悬浮模型进行有限元仿真,其磁场理论值、仿真值、实际值曲线如图7所示。在平衡点附近,实际值与仿真值基本一致。部分计算与仿真结果如表3所示。
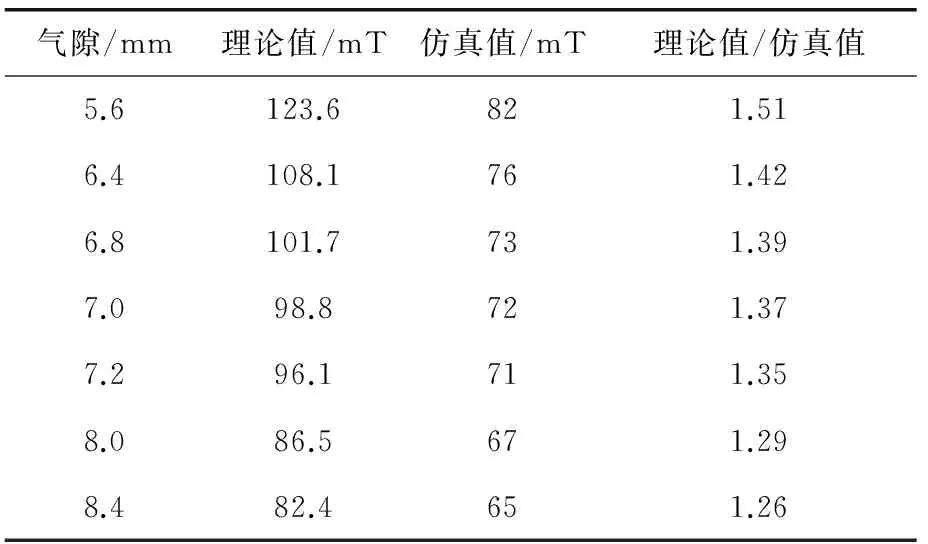
表3 计算与仿真结果
由于δ0≪δ,可以忽略δ0对δ的影响,理论值与仿真值的比值即为1+λ在平衡点附近发生较小位移时的值。由表3可知,可以近似认为λ在平衡点附近为一常值。
4 气隙观测函数的设计
采集电路与悬浮电路结构设计如图8所示。闭合开关2与开关3,断开开关1,使得悬浮物在传统模式下稳定悬浮。在平衡点附近上下拽动悬浮物,采集实时的气隙、电流以及磁场信号,根据式(4)的形式进行拟合。闭合开关1,断开开关2与开关3,将拟合函数运用到悬浮控制中,从而实现无气隙传感的悬浮。
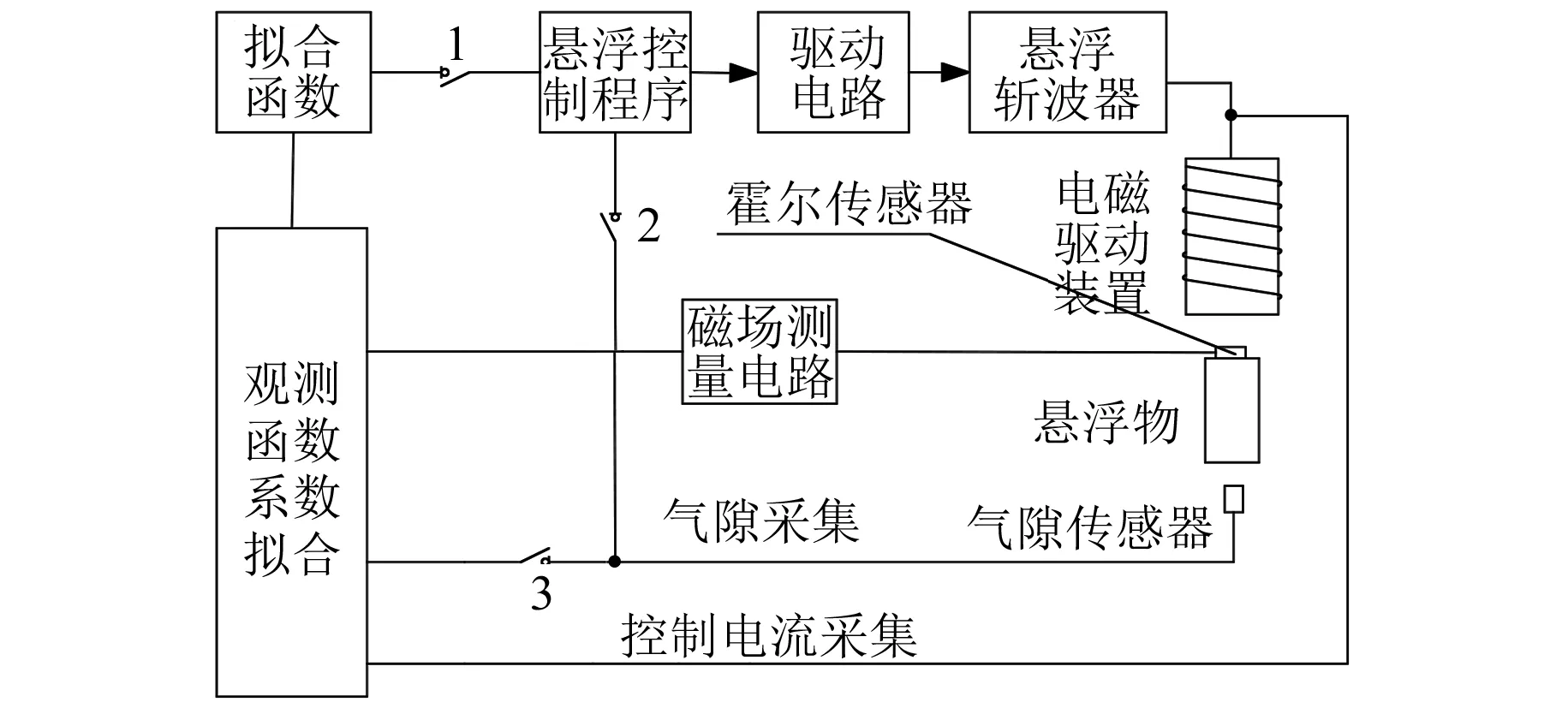
图8 采集电路与悬浮电路结构
4.1 观测气隙的拟合
加入霍尔传感器和磁场测量电路,采集悬浮物在平衡点周围的磁场测量电压、线圈电流以及气隙值。采用两种方法对这些实测数据开展分析,进行观测气隙拟合。
方法一:非线性曲线局部线性化。将式(4)在平衡点附近展开,并忽略二阶及其以上项,有:
δ=f(i,B)=Δδ+δ1=
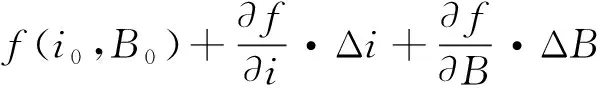
(7)
式中:i0为平衡点的电流值;B0为平衡点的磁感应强度值;δ1为设定的气隙参考值;Δδ为实际气隙与参考气隙的差值。
将f(i0,B0)=δ1代入式(7)有:
Δδ=KI·Δi+KB·ΔB
(8)
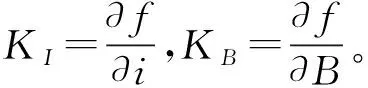
此方法可以很好地解决平衡点线性化的问题,但拟合函数中有两个变量,增加了函数拟合的复杂性。此外,这种方法只在平衡点附近很小的范围内适用,当有大扰动发生时,最终的控制效果会偏离预期。
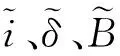
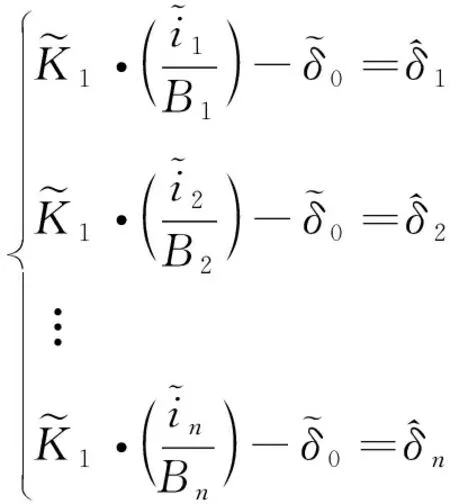
(9)


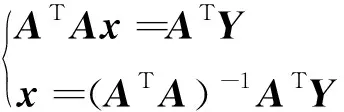
(10)
通过试验测得的部分数据如表4所示。

表4 实测数据
4.2 观测气隙试验
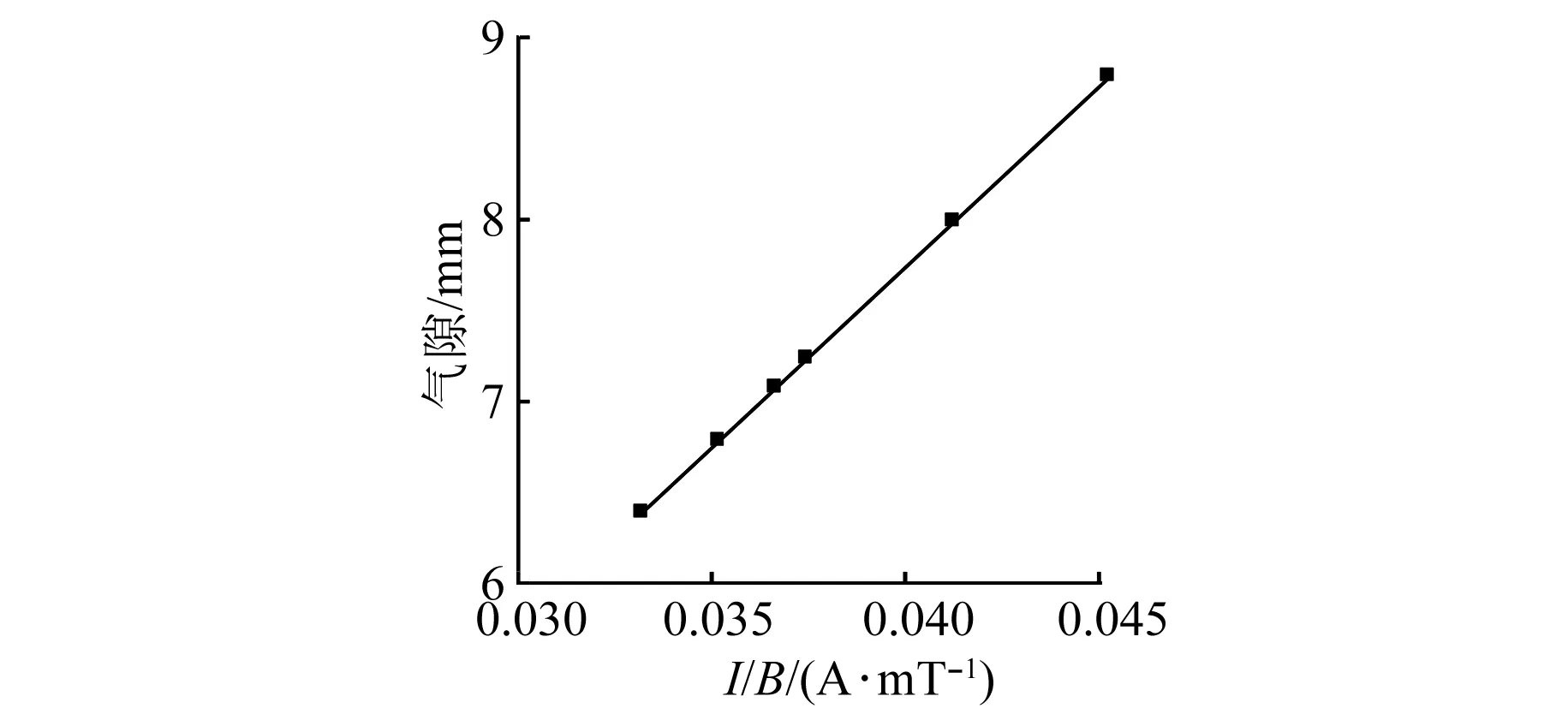
图9 气隙函数拟合曲线
为了确定气隙观测函数的可靠性,在平衡位置附近上下拽动悬浮物,绘制了实际气隙曲线与观测气隙的动态波形,如图10所示。
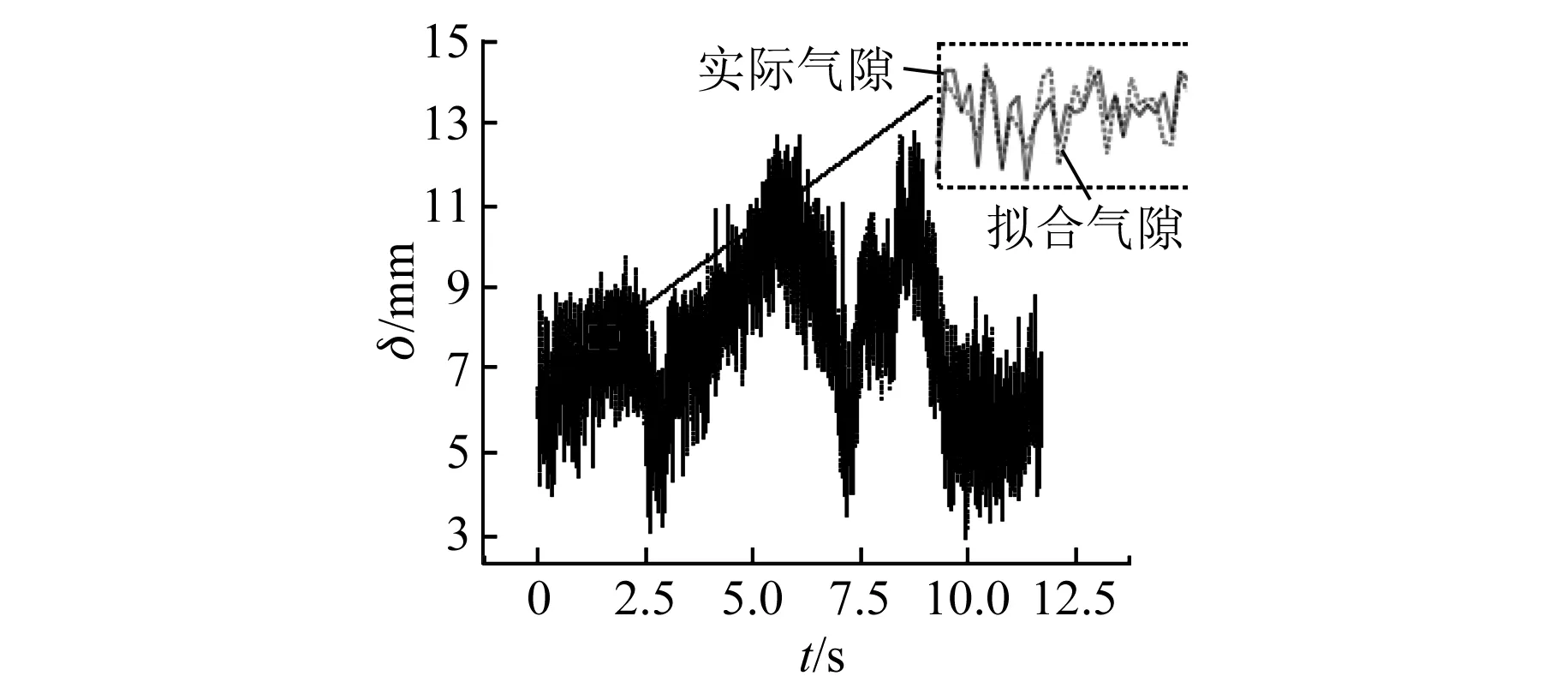
图10 实际气隙与观测气隙动态波形
由图10知,观测气隙可以跟随实际气隙。
5 观测气隙的仿真与分析
5.1 观测参数对闭环系统的影响
采用PD控制下悬浮系统的动力学方程组为

(11)
式中:m为悬浮物质量;g为重力加速度;F为所受磁场力;fd为外界干扰;kp、kd分别为控制系数。
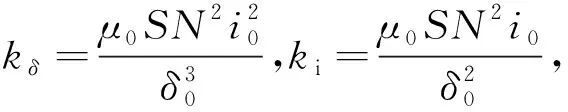

(12)
式中:k′d=kdki,k′p=kpki-kδ。
采用观测气隙作为反馈有
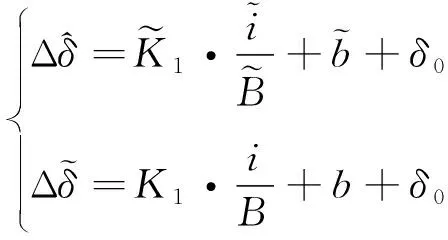
(13)
则:

(14)
将式(14)代入式(12)得:
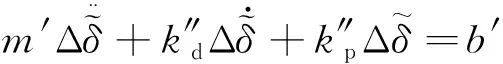
(15)
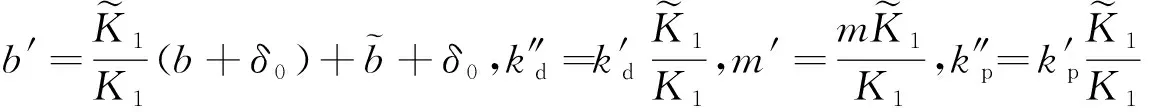

(16)
5.2 观测气隙在闭环系统中的控制仿真
为了验证试验的可行性,根据图6在Simulink仿真条件下搭建了传统控制方式实现悬浮物在气隙为7 mm处的悬浮模型,并将拟合的气隙观测函数加入气隙辨识模型中,如图11所示。
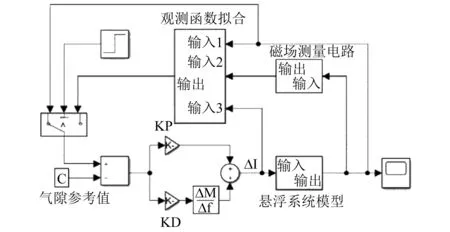
图11 Simulink仿真模型
为了检验气隙观测函数的可靠性,在模型中加入方波扰动。两种不同控制方式下的气隙响应曲线如图12所示。
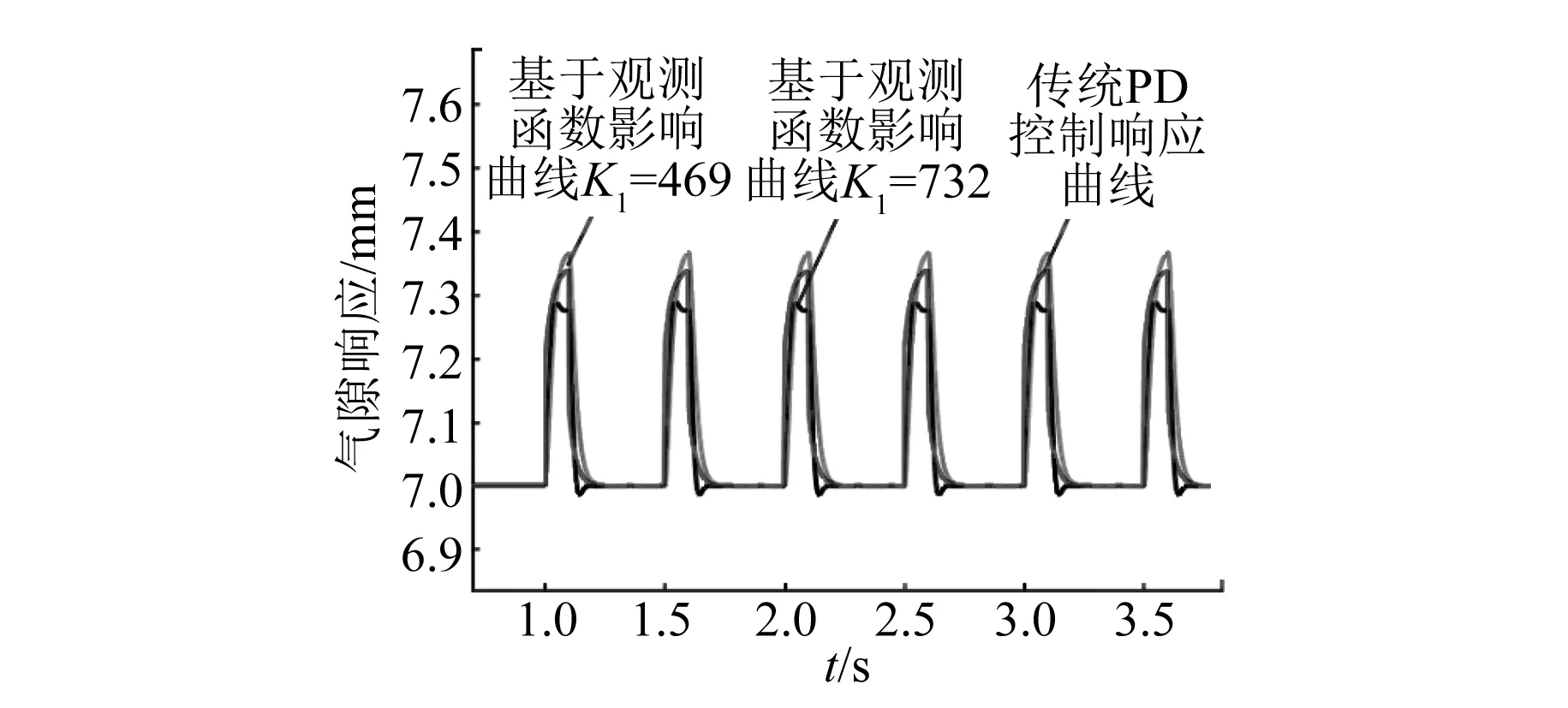
图12 两种控制下的响应曲线
由图12可知,基于霍尔传感器的悬浮控制在扰动下的响应与传统PD控制响应基本一致。
6 试 验
现将得到的气隙观测函数应用到悬浮控制电路中。由于没有使用气隙传感器,在放入悬浮物之前在电磁铁中通入I=2.5 A的电流产生磁场,然后将悬浮物放到平衡点附近,待磁场检测电路检测到有输出电压时取消恒定电流。实际悬浮效果如图13所示。

图13 悬浮试验平台
绘制悬浮物的浮动波形如图14所示。由图14可知,通过气隙观测函数作为气隙反馈的方法,可以实现悬浮物在气隙为7 mm处的悬浮。

图14 悬浮物浮动曲线
7 结 语
提出了一种基于气隙辨识的无气隙传感器悬浮系统,推导了气隙与电流和磁感应强度的数学模型,利用有限元仿真软件对数学模型进行仿真。分析了利用拟合气隙作为气隙反馈的方法,并将拟合函数应用到悬浮控制系统中。试验表明,悬浮物实现了在气隙为7 mm处的悬浮。
