轨道板温度场非线性特征分析

2022-08-09何越磊赵彦旭路宏遥

铁道标准设计 2022年8期

程琴,何越磊,赵彦旭,路宏遥

(1.上海工程技术大学城市轨道交通学院,上海 201620； 2.中铁二十一局集团有限公司,兰州 730070)

引言

CRTSⅡ型板式无砟轨道具备多种优异特性，使其被广泛应用于我国高速铁路建设中。但因长期暴露在大气环境下，CRTSⅡ型板式无砟轨道结构会在环境温度影响下产生变化，轨道板表面升温时整体会出现“外热内冷”的状态，降温时则会“外冷内热”，从而使结构内部产生较大的垂向温度梯度，受温度梯度影响会引起一定的翘曲变形[1]。翘曲变形在受约束情况下使轨道结构内部产生温度应力[2]，应力超过混凝土抗拉强度时，会导致轨道结构产生层间离缝现象[3]。这些由温度荷载引起的病害将严重影响高速铁路运营速度与安全，并会对轨道板运维管理技术提出较高要求。因此，对环境温度影响下轨道板温度场分布特征及规律进行分析，对于提升轨道板运维管理技术水平具有重要意义。

近年来，对无砟轨道结构温度场的研究日渐增多[4]，主要分析方法可归纳为两类：一类是统计分析法[5-6]，根据实测数据统计并分析轨道板温度场各影响因素之间的关系；第二类是理论分析法[7-8]，通过搭建有限元系统，对自然环境模拟状态下的温度场进行数值分析。但现有分析中，从轨道板温度场的混沌特性角度进行研究相对较少。

基于此，在对环境温度影响下CRTSⅡ型板式无砟轨道温度场分析中，通过相空间重构手段对一维温度时间序列进行维数扩充，以充分挖掘温度序列内部所蕴含的信息及规律，并结合PCA方法消除轨道板温度时间序列各成分间的信号自相关性，提高序列复杂度，最后根据计算得到轨道板温度序列的排列熵值，对轨道板温度场非线性特征进行剖析，为提升轨道板运维管理技术水平提供理论支撑。

1 基本原理

复杂度是用来反映非线性时间序列无序程度的重要参数。受环境温度、太阳辐射等因素影响，轨道板温度场分布具有典型的混沌特性[9]，使输出时间序列具有非线性、非平稳性和不确定性的特点。目前，复杂度测量的多种方法中，熵值法被广泛应用于混沌特征识别及复杂度的度量研究中，选取其中的排列熵法[10]作为分析轨道板温度序列的方法。目前，常用的非线性信号检测方法[11]多是基于量化相空间中最近点的性质进行概率统计，算法繁琐且计算量较大。与其相比，排列熵算法通过计算，定量阐述序列的复杂度[12]并放大信号的微小变化[13]，体现序列中的异常，算法简单，计算速度快，对于系统信号的突变异常检测具有十分重要的意义[14-15]。

1.1 排列熵算法原理

排列熵算法基于Kolmogorov复杂度算法，融合了信息熵的概念，是一种用于计算序列复杂程度的突变检测方法[16]，可检测系统发生突变的时刻并放大信号的微小变化[17]，算法步骤如下。

步骤1：采用相空间重构方法，对长度为N的系统离散时间序列{xi，i=1，2，…，N}进行重构，得

X(i)=[x(i)，x(i+τ)，…，x(i+(m-1)τ)]

1≤i≤N-(m+1)τ

(1)

其中，m、τ为重构嵌入维数和延迟时间，当τ=1时，可以得到最大程度的重叠。

步骤2：对X(i)的m个重构分量x(i)，x(i+τ)，…，x(i+(m-1)τ)，按照由小至大的顺序进行重新排列，得到x(i+(jm-1)τ)，1≤j≤m。如果在分量序列中出现两个值的x(i)相同，则按照j值的大小确定排序。因此，任意一组向量X(i)都可以得到与之相对应的符号序列，即

A(g)=[j1，j2，…，jm]，g=(1，2，…，q)，1≤q≤m!

(2)

步骤4：则此时时间序列的排列熵可定义为

(3)

(4)

因此，用排列熵检测突变的过程即描述为：将一个时间序列按所选时间窗大小分为若干个长为w的子序列，各子序列之间的重叠概率可根据研究对象自由选定，计算其排列熵值h(p)，并观察其动态变化的情况。由于轨道板的温度场分布具有典型的混沌特征，所以轨道板温度时间序列的非线性特征可以从h(p)的变化中体现出来。对轨道板温度的排列熵计算中采用最大重叠；对于子序列长度w的选取，为保证其统计学意义和精确度，不能过大或过小；算法中的参数m，其取值范围一般为3≤m≤15。

1.2 算法参数选取原则

在排列熵计算过程中，对于参数的选取，选用自相关函数法[18]获取恰当的延迟时间，选用G-P法[19]获取恰当的嵌入维数。以具有标准混沌特性的Lorenz方程x分量的时间序列为例进行说明。

将Lorenz方程x分量的时间序列作为定义的一维时间序列输入自相关函数，所得结果如图1所示，选定自相关函数值下降到初始值的1-1/e倍时，所得到的时间τ即是所需最佳延迟时间，即Lorenz方程x分量的延迟时间为23。

图1 Lorenz方程x分量自相关函数曲线

在自相关法已获得适当延迟时间的基础上，将Lorenz方程x分量的时间序列作为定义的一维时间序列输入，进行G-P算法运算，所得双对数曲线如图2所示，其中C为关联积分计算值，r为搜索半径，对其中的线性部分，用最小二乘法进行拟合，得出一条最佳拟合线段。该线段斜率称为关联维数。其会随着嵌入维数增大而增大，最后达到饱和值，即为关联维数D，选定嵌入维数m≥2D+1的值为最优嵌入维数，即Lorenz方程x分量嵌入维数为8。

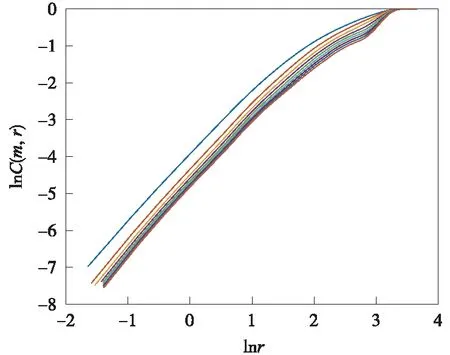
图2 Lorenz方程x分量双对数曲线

1.3 算法有效性验证

由于轨道板温度场具有混沌特性，为验证利用排列熵算法检测其状态变化是否具有可行性，对非线性动力学系统Logistic模型xn+1=μxn(1-xn)进行例证操作，结果如图3所示。其中，xn∈[0，1]，n=0，1，2，3，…，μ为控制参数。Logistic方程是用于研究某一范围内某种昆虫繁衍时的子代数量问题。图3(a)给出了2.5<μ<4时，该二次迭代系统终态图。由图3(a)可知，当μ∈(2.5，3)时，系统经过有限次迭代后收敛至排斥不动点0和吸引不动点1-1/μ；μ∈[3，μ∞)时，模型轨道出现了周期行为特征即倍周期分岔现象；当μ∈(μ∞，4)时由倍周期阶段转为混沌状态。即可知序列按稳定不动点、不稳定不动点、周期、混沌4个阶段进行演化突变。

结合图3(b)分析可知，当时间序列发生阶段演化时，排列熵的变化均与模型终态图演化趋势一致，当Logistic模型发生状态变化时，其时间序列的排列熵值也表现出明显的对应变化。由图3(b)可知，排列熵可检测并放大非线性系统时间序列中的微小变化，当序列向混沌演化时，其对应的排列熵值也逐渐增大并趋向于1，即混沌程度越高值越大。由于轨道板温度场具有混沌特性，所以轨道板温度时间序列的非线性特征可从熵值的变化中体现出来，熵值越大，复杂度越高，非线性程度越高，即轨道板内温度序列变化越明显趋向异常，可将排列熵法用到轨道板温度场的监测分析。

图3 Logistic终态及排列熵随控制参数μ的变化曲线

2 轨道板温度序列排列熵分析

2.1 温度序列的数据来源

选取华东某客运专线CRTSⅡ板式无砟轨道结构为研究对象，线路运营速度为300 km/h。分别在无砟轨道板板表、板中、板底安装温度传感器，以1次/30 min的频率获取一整年轨道板温度及气象温度变化数据，采样长度为14 848个点，得到动态温度时间序列如图4所示。由图4所示，随着气温的不断升高，轨道板温度也不断增大，夏季结束之后气温降低，轨道板温度也随之减小，可见轨道板温度变化与环境温度变化趋势相一致，且轨道板表面温差变化值大于气象温差变化值，但由于轨道结构内部温度场的复杂特性，结构内部温度的变化随轨道板深度加深表现出不均匀性，温差幅值随距离轨道板面深度增加有变小趋势。

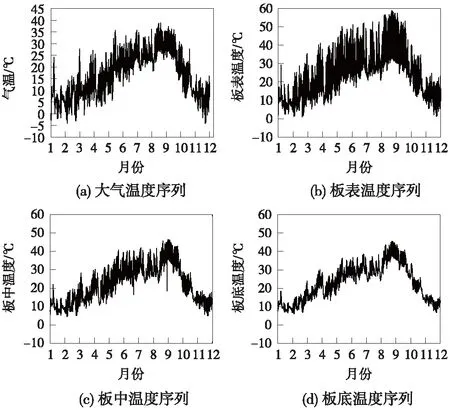
图4 轨道板温度时间序列

2.2 计算结果分析

轨道板温度场的变化与气候系统的非线性、复杂性、耗散性及轨道板内部结构各因素的相互作用紧密相关，因此，利用传感器采集数据手段，在较长时间内获得的温度序列只能从部分变量的角度对轨道板温度场进行观测，无法得到温度场所有状态变量的演变规律。为从少数甚至单一的数据序列中获得整个系统相空间的信息，对轨道板温度序列进行相空间重构[20]。此操作关键在于选取最优时间延迟τ和嵌入维数m，进而在重构所得的高维空间中深入分析时间序列，以提高分析的准确性。按前述参数选取方法，选取m=7，τ=5，w=500为最优参数，计算温度序列的排列熵。

混沌序列的自相关性越强，序列随机性越差，复杂度越低，故去除混沌序列的相关性，得到更高复杂度的混沌随机序列，也是要解决的问题。为简化分析，采用主成分分析对相空间重构后得到的高维空间进行处理，使原始序列的自相关性在经过主成分分析线性变换后得到降低，以便在处理后的序列中充分揭示轨道板温度梯度的混沌特征。

目前，关于主成分的选择，常用方法有两种，一种是主成分回归法，另一种是主成分贡献率累积百分比法，本文选用后者。对重构后得到的相空间，按每一列定义为一组向量，计算其协方差矩阵，并求其特征值及特征向量，最后将特征向量转置得变换矩阵。选定累计贡献率达到85%的部分为所需主成分，并按变换矩阵对序列进行主成分变换，进而进行温度序列的排列熵值计算。计算结果如图5所示。

图5 轨道板温度序列排列熵值

轨道板温度序列的排列熵值表现出与环境温度变化相一致的规律性，且由于轨道板表面与大气环境接触最充分，由图5可以看出，轨道板表面温度序列排列熵值随环境气温的变化最明显。

由图5可知， 4月份气温最低值为7.3 ℃，而3月份最低气温为-2.8 ℃，5月份最低气温为4.3 ℃，且4月份整体温度均高于5月份。可知4月份气温增长速度及幅值高于平均气温变化水平，排列熵值在4～5月份处也相应发生了明显的变化，其中，以轨道板表面的变化最为明显，由原先的0.424增加至0.562。

运营维护中，高温季节尤其是持续高温天气(连续3d及以上日最高气温在35 ℃以上，同时日温差小于10 ℃)情况下，轨道整体温度也会随之升高且远高于气温，板内也会出现较大的温度梯度，会加剧轨道板的翘曲变形。图5中7～9月份最低气温已增加至25 ℃，最高气温也达到33 ℃～38 ℃，随着温度不断升高，轨道板内温度序列的排列熵也不断增加至最大值0.602。10月份温度突然降低且降速较快，排列熵值也表现出较大的波动性变化，其中，以轨道板表面变化最为明显，由原先的0.596降低至0.413。

正常温度变化情况下，轨道板温度序列的排列熵值变化幅值小于异常温度变化情况下的排列熵值。即证明排列熵可有效检测到序列中的非线性变化，并通过排列熵值的变化放大体现出来。这也直观说明需加强对轨道板温度场的动态监测。根据本文所得结果，为实际养护维修设置排列熵阈值上限为0.6，阈值下限为0.4，以判别轨道板温度场状态是否正常。此外，当排列熵值变化幅值超过0.15时，也需及时安排结构检查[21]。

对比板表、板中、板底排列熵值随时间的变化可知，由于轨道结构导热性能差引起结构内部温度变化随深度的增加存在滞后性，也充分体现在排列熵值的大小上，即随着轨道板表深度增加，板中、板底温度序列的排列熵值在不断减小。以上分析表明，研究结果与轨道板温度场的特性、变化趋势及排列熵特征相符，排列熵能够较好地衡量轨道板温度序列的复杂度，检测轨道板温度场的状态变化。