铁路工务管理单元的动态不平顺综合评价
2022-08-09李远富
钟 萍,尹 航,李远富
(1.西南交通大学土木工程学院,成都 610031; 2.四川大学商学院,成都 610065;3.四川旅游学院信息与工程学院,成都 610100)
引言
截止2020年底,我国“四纵四横”铁路网已经形成,“八纵八横”正在推进,铁路运营里程超过14万km。为保持铁路系统的安全性、可靠性,修理资源合理性,最大限度地利用该系统的能力,对铁路质量进行检查、检测、评价和维护管理是至关重要的。目前,对线路养护维修存在一定盲目性,经常出现工务部门日常维修工作没有很好地计划顾此失彼的现象。如何实现工务作业“干得准、干得好、干得多”的目标,一直是困扰工务系统的难题。
目前,我国线路检查有人工静态检查、动态检测两种方式[1]。对于各铁路局工务部门通常都是对各种检测数据进行简单的扣分打分,进行评价各线路段的质量好坏。徐金辉等[2]指出了轨道不平顺性评价中均值管理评价与峰值管理评价各自的特点,并且指出了截止波长对这两种评价方法均有影响,建议利用截止波长改进现有的评价方法;董英荣等[3]比较了均值管理法、峰值管理法在对轨道质量评价时的各自优缺点,指出这两种方法需要改善,国内对于结合这两种指标进行综合评价的研究鲜少;王俊文[1]提出利用轨检车检查、机车车载式轨道动态监测系统和静态检查这三类数据分别量化为3个指标,对不同等级和特点的线路通过试验研究赋予3个指标不同的权值,从而得到线路设备综合质量状态评价。
发达国家的轨道管理不仅使用工务管理信息系统,还利用最新的GIS技术、信息技术、检修维护技术,以此来提高轨道质量的检测和维护水平[4-6]。KHOUZANI[7]建立了轨道退化模型,以最小化轨道维护成本和保持高轨道几何状态质量;MACCHI[8]建立铁路系统的可靠性模型,并建立系统可靠性和运输服务水平之间关系的模型,采用RBD建模方法,以评估项目故障对系统级别的影响;BURROW[9]等开发基于概率模型的工具研究,该工具能够确定在任何预算情景下维护对铁路网络养护状况的影响。
为保证线路的安全和高平顺性,工务部门往往需要花费大量的人力、精力、财力来检修。因此,对线路动态不平顺性进行评价有助于病害计划编制准确性、科学性。目前,对轨道动态不平顺评价主要依据的是峰值和均值管理,采用扣分法来确定每km线路单元的质量。峰值管理和均值管理存在不足:①当轨道属于局部不平顺状态时,适合使用峰值管理方法,因为当存在的局部超限点个数有限时,使用均值管理计算方法常得到轨道状态与实际不符;②轨道属于周期不平顺时,适合使用均值管理法[3]。
基于上述实际情况,建立一个有效的综合评价体系是必要的,将峰值、均值管理整合,运用数学模型计算出综合评价值,提高效率。在已有线路单元划分基础上,运用数学模型对线路单元动态不平顺性进行综合评价,对线路单元进行排序,目的是为工务维修管理的决策提供有力、直观、科学依据。
1 线路管理单元综合评价概述
1.1 线路管理单元
铁路工务管理单元:铁路线路具有带状分布特点,为方便工务部门对线路管理以及检测、监控轨道的质量状态及其变化,对线路按照一定规则划分成一定长度的多个小单元区段,这些小单元区段称之为基本管理单位,我国的基本管理单位长度为200 m,法国为300 m,日本为500 m[10]。
划分线路管理单元,方便对线路的基础数据收集。线路管理单元的综合评价是利用线路管理单元峰值和均值的数据,建立适当的模型,对线路管理单元质量做出评价。线路管理单元的综合评价对于建立线路单元质量均衡体系非常关键。线路单元质量均衡体系是新型综合工务维修管理模式和体系。采用以TQI检测的基本单元200 m作为一个小单元,综合考虑生产力布局、线路线形条件、轨道条件、检测数据特点等因素,在小单元基础上以3~4 km为一个大单元,把线路划分成若干个直线单元、曲线单元、道岔单元的线路单元划分方式[8]。
1.2 综合评价指标选择
在线路单元划分基础上,选择合适线路单元指标,运用合理方法评价轨道状态是对线路单元管理的关键,为评价轨道的动态不平顺性,目前采用超限峰值扣分法,通过计算轨道质量指数(TQI)来管理区段内轨道不平顺[11]。超限峰值扣分法是依据国家铁路线路修理规则规定的铁路不同速度、4种等级下,每千米轨道各个检测点的动态不平顺各参数的检测值与容许偏差管理值比较后进行百分制扣分打分,得到每千米扣分总和,以此来判断每千米线路质量状态(偏差越大,扣分越多,线路不平顺性越大)[12]。
根据文献[10]划分管理单元,再综合考虑铁路局数据采集方式,将评价对象定为1 km 单元,这与我国采用峰值均值扣分对象一致,便于比较综合评价法评价结果与峰值均值扣分法得到结果是否一致。本文将探讨根据峰值管理和均值管理数据,将均值、峰值整合,利用基于熵权法的灰色关联评价模型,对线路的动态不平顺性进行综合评价。
采用综合评价指标体系包括均值和峰值。均值包含TQI及其单项值,峰值包含各轨道动态几何值,指标体系如表1所示。

表1 线路单元评价指标体系
2 基于熵权法的灰色关联分析法
2.1 熵权法确定权重
文中线路单元评价指标有两类共14个指标,每个指标在线路单元评价中的重要程度不同,每个指标权重体现了指标在整个评价体系中的重要程度,故指标权重确定是线路单元评价的关键一步。权重一般采用简单算数平均方法、AHP法和均方差法等确定,这些算法存在很强的主观性。
熵权法是一种客观的赋权法,在确定指标权重中较为广泛应用。线路单元综合评价采用熵权法确定权重,从而避免权重的主观性。熵权法确定的权重大小是根据评价指标本身信息的效用值大小来映射权重[13]。
信息熵大小决定了权重的大小,某个指标信息熵越小,表示这个指标所含的信息量越多,指标权重越大以及指标在评价中作用也越大[14-15],计算过程如下。
(1)数据标准化
若有m个评价对象,n个评价指标,则构成的决策矩阵为
R=(xij)m×n(i=1,2,…,m;j=1,2,…,n)
(1)
由于信息熵是一个无量纲值,因此,需对式(1)中数值进行标准化处理[16]。由于本文数据值越大,表示不平顺性越大,所以采用正向指标进行标准化处理,得到归一化后的矩阵
B=(bij)m×n(i=1,2,…,m;j=1,2,…,n)
(2)
(3)
式(3)中,bij是xij标准化处理后的结果;min(xj)是变量x的第j项指标在研究期间最小值;max(xj)是x的第j项指标在研究期间最大值。
(2)极端值平移变换
极端值(比如零)会经常出现在对数据进行处理的过程中[17],熵权法中数据都必须大于零,对于原始数据中出现的极端值,不能直接删除,需对数据进行处理,即进行数据的平移变换[18]。过程如下
yij=cj+bij×dj
(4)
(5)
(6)
经过极端值平移变换后的矩阵记作
Y=(yij)m×n
(3)确定评价指标的熵
根据熵的定义,m个待评价对象,n个评价指标,可以确定评价指标的熵为
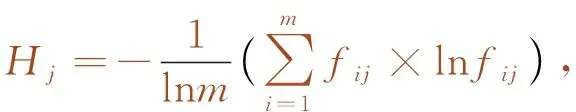
(7)
为使ωlnfij=1有意义,一般需假定当fij=0时,fijlnfij=0。但当fij=1,lnfij=0,这显然不切合实际,与熵的含义相悖,故需对fij加以修正,将其定义为
(8)
(4)计算评价指标的熵权
ej=1-Hj
(9)
(10)

由此得到线路单元评价14个指标的权重值。
2.2 灰色关联分析
在熵权法确定权重大小后,利用灰色关联分析法对线路动态不平顺性进行综合评价。灰色关联分析法是通过研究参考序列与比较序列之间曲线的几何相似程度来判断两者的差别程度,关联度越大,说明参考序列与比较序列的关系越紧密,曲线越接近,这两者的变化趋势越一致[19-21]。
灰色关联分析优点在于对样本的大小、是否有规律均无要求,且计算量小,计算简单,评价结果与定性分析结果相符。利用灰色关联分析法对线路动态不平顺评价,得到关联度大小不是最主要的,重要的是根据关联度大小排序得到线路的不平顺性排序[22]。计算步骤如下。
(1)确定参考序列与比较序列
将权重向量W与标准化后矩阵B相乘,构造加权矩阵
V=(vij)m×n=(wj×bij)m×n
(11)
在加权矩阵V中,设由n个评价指标最优值组成的数据序列为参考序列,记为v0(j)
v0(j)=(v0(1),v0(2),…,v0(n))
(12)
设第i个评价对象的指标值组成的数据序列为比较序列,记为vi(j)
vi(j)=(vi(1),vi(2),…,vi(n))
(13)
(2)计算两级最小差和两级最大差
计算比较序列vi(j)与参考序列v0(j)之间的差值
Δvij=vi(j)-v0(j)
(14)
两级最小差为
(15)
两级最大差为
(16)
(3)计算灰色关联系数
(17)
式中,ρ为分辨系数,{ρ│0≤ρ≤1},通常取ρ=0.5。
(4)计算灰色关联度
评价结果是线路单元灰色关联度越大,越接近取样本最大值的参考序列,说明线路的不平顺性越大;相反,线路单元的灰色关联度越小,越远离参考序列,线路的不平顺性越小。对各个评价单元的关联度进行排序,得到各线路单元综合评价排名[17]。
(18)
3 应用研究
3.1 案例背景
京九铁路呈北南走向,北起北京西站,南至香港红磡站(九龙车站),1992年10月全线开工,1996年9月1日建成通车。线路长度2 407 km(干线路段),设计速度为160 km/h(改造)。
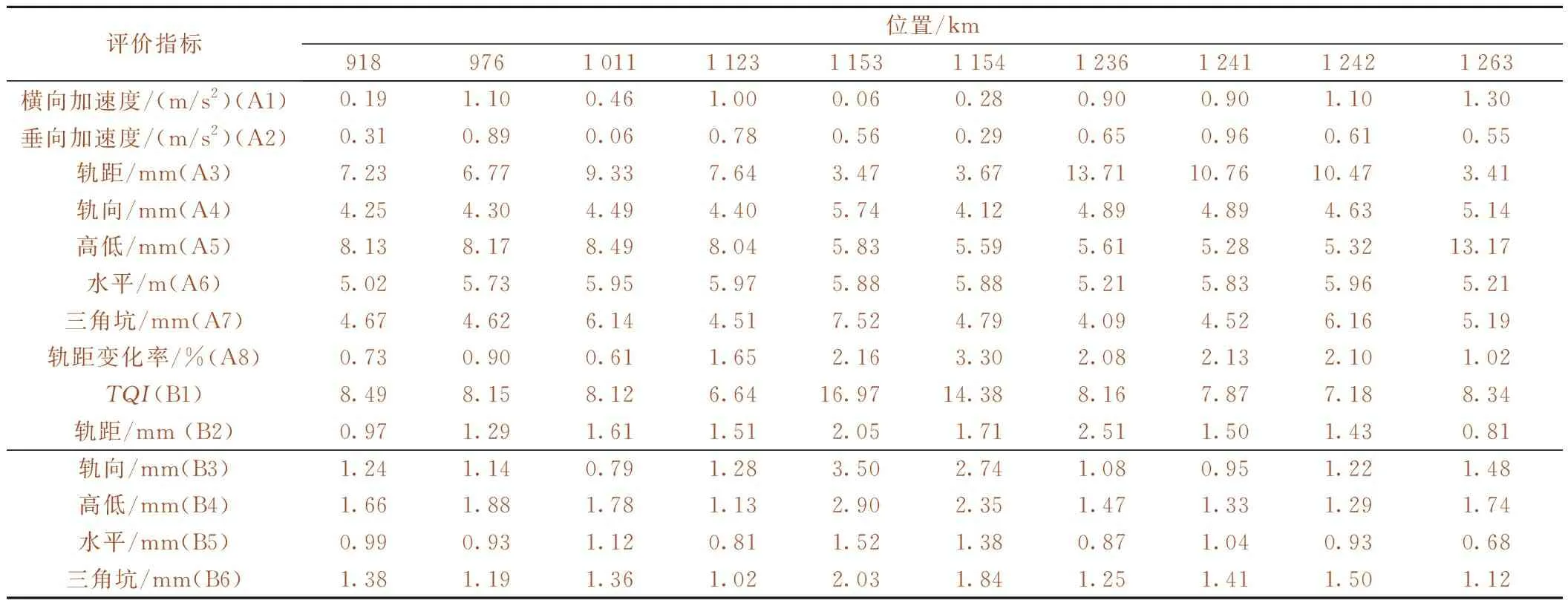
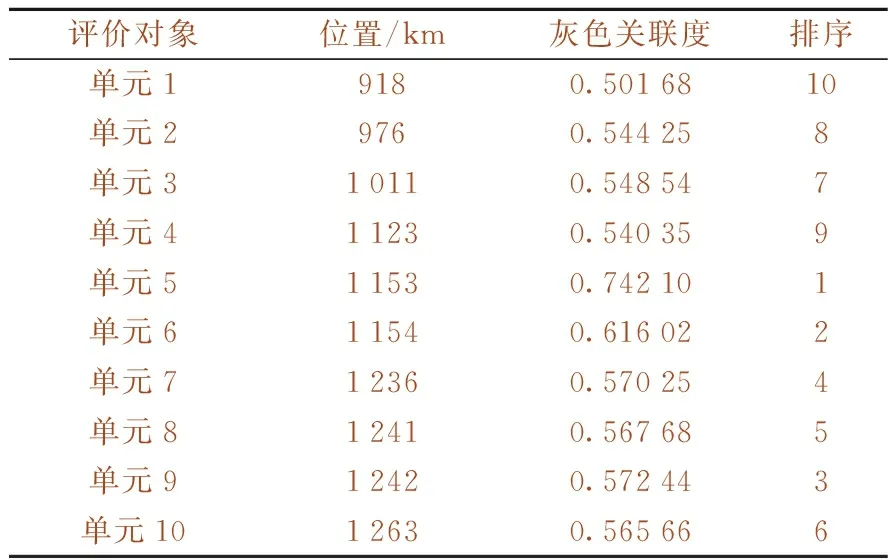
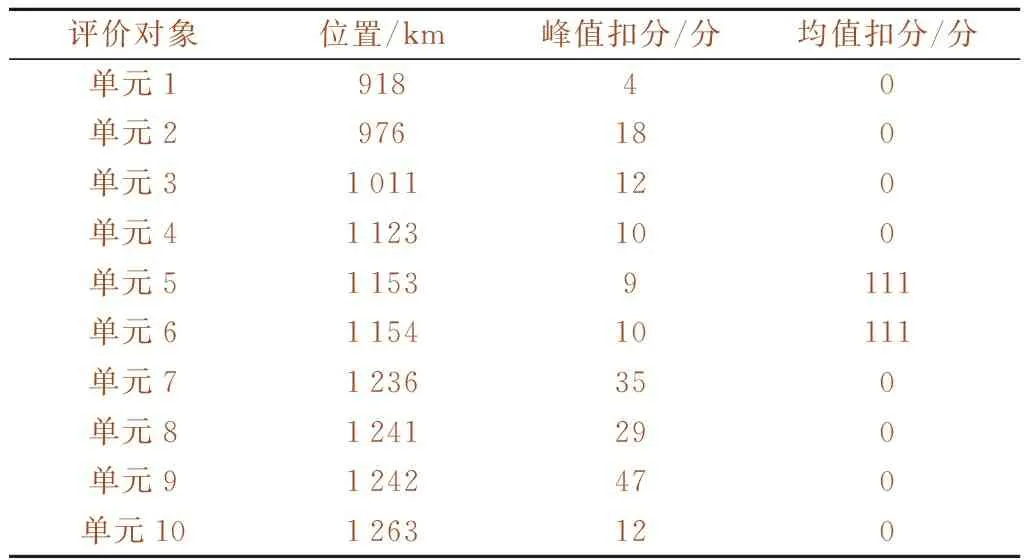
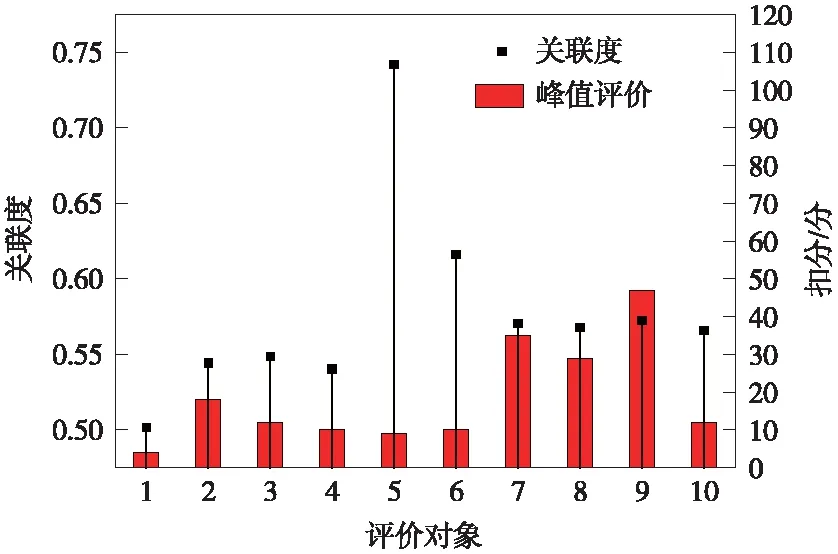
采用某铁路局某工务段京九线下行的数十个数据,以每1 km单元作为评价对象,对线路单元进行综合评价。考虑到京九线设计时速,依据《普速铁路线路修理规则》(2019年1月)摘录了120 km/h 表2 轨道动态几何不平顺容许偏差峰值的管理值(120 km/h 表3 轨道质量指数管理值(120 km/h 按照下述步骤对原始检测数据进行处理。 (1)如在同一个1 km单元线路内,同一个指标有多个不同值,对于这样线路单元指标值规定取原始数据最大值。 (2)由于某铁路局工务段给出原始数据只有超限指标有数据,且分Ⅰ级超限、Ⅱ级超限、Ⅲ超限、Ⅳ级超限,某些没有达到超限值指标的数据未给出,对于没有超限的指标值,本文采用0~相应指标最小偏差管理值的随机数进行赋值,如实际中对于没有达到超限值的数据有原始数据,直接使用实际原始数据。 (3)均值的检测值是针对200 m线路单元,对于文中1 km的评价对象,取相应每km内均值的最大值作为评价对象的原始数据。 最终经过处理后的原始数据见表4。 表4 单元指标值 3.2.1 权重确定 根据表4的原始数据,由10个评价对象,14个评价指标构成了10×14的决策矩阵R。利用式(1)~式(10)对数据进行标准化处理,由于数值中出现零的这种极端值,因此,需对数据进行平移转换,然后计算各项指标的信息熵和信息熵冗余度,最后得到各项指标的权重。各项指标权重结果见表5。其中,权重最高值为0.136 92,权重最低值为0.029 62,相差为0.107 3。 3.2.2 灰色关联度确定 根据式(11)将权重向量W与标准化矩阵B相乘,构造加权矩阵V。利用式(12)、式(13)确定出其中的参考序列、比较序列。再根据式(14)~式(18),计算出各参考序列与比较序列差值、参考序列与比较序列两级最小差以及两者的两级最大差,从而得出各评价对象的灰色关联系数,最终计算出各评价轨道单元的灰色关联度。 本文参考序列取值为同一指标中各个比较单元的数据最大值,数据越大说明轨道越不平顺。各单元灰色关联度见表6。表6中各个工务维修管理单元关联度值大小属于[0,1]区间范围,其中,工务维修管理单元5的灰色关联度最大,其值为0.742 10;工务维修管理单元1的灰色关联度最小,其值为0.501 68。 表6中得到的各个管理单元的灰色关联度即为最终综合评价值。在灰色关联度排序中,一般一个管理单元的灰色关联度越大,越接近参考序列,排名越靠前,表明轨道越不平顺。表中关联度的大小并不重要,重要的是关联度排序。工务部门能依据综合评价排序结果有计划进行日常维修,对轨道不平顺度越大的优先进行维修。 表6 各单元灰色关联度 3.2.3 综合评价法与现有扣分法比较 根据中国铁路总公司《普速铁路线路修理规则》(2019)局部峰值评价和区段均值采用扣分法评价,某铁路公司得到各评价对象局部峰值和区段均值的扣分,见表7。各评价对象的关联度与峰值扣分比较见图1,关联度与均值扣分比较见图2。 表7 评价对象扣分 图1 关联度与峰值评价 图2 关联度与均值评价 表7中,某铁路公司工务段按照峰值总扣分≤50标准认定10个评价对象为优良单元,但根据区段均值评定标准,单元5和单元6却应列入维修计划尽快安排修理,其他单元均为质量均衡,无需维修。故采用扣分法进行动态几何不平顺评价时,必须综合考虑峰值和均值,二者均对线路单元质量至关重要。 基于熵权法的灰色关联分析法,得到各个评价对象的关联度排序中单元5的关联度最大,单元6关联度次之,单元5和单元6质量最差,这与某铁路局工务段利用扣分法得到结果一致。 在图1中,根据峰值扣分,单元9与单元7扣分最高且均≤50,且10个评价单元均属于优良单元。而根据关联分析法得到单元9关联度为0.572 44,关联度排序为第3,单元7关联度为0.570 25,关联度排序为第4,这两个单元并不是关联度最大的单元。 图2中根据均值扣分单元5和单元6扣分相同且最高,属于优先列入维修计划的单元,其余单元扣分均为零。根据关联度大小排序,单元5关联度最大,单元6次之。说明单元5轨道不平顺度最大,单元6次之。 在图1、图2中,虽然单元3与单元10的均值扣分均为零,峰值扣分均为12,但这两个单元的关联度是不同的,单元10的关联度大于单元3。某铁路局工务段提供原始数据中单元10存在2处峰值属于Ⅱ级超限,2处指标峰值属于Ⅰ级超限,而单元3中12处峰值均属于Ⅰ级超限,虽然单元3与单元10峰值与均值扣分均相同,从原始数据中可以断定单元3质量优于单元10。这与根据本文关联度评价结果一致。 因此,对于使用峰值均值扣分法时需将两者结合考虑,才能正确判断轨道线路单元的动态不平顺性,本文使用基于熵权法的灰色关联分析法进行线路动态不平顺性综合评价正是结合峰值与均值,得到结果与实际一致。 铁路工务管理需统筹考虑多方因素,目前我国采用的评价方法和准则并不成熟,现有评价方法中的峰值管理和均值管理经常会出现相互矛盾的情况。故提出基于熵权法的灰色关联分析法将峰值和均值两者结合,充分利用峰值和均值扣分法呈现互补特性,结合两种方法各自优势,构建了管理单元轨道动态不平顺综合评价新方法,经验证,此方法评价所得排序结果与实际相吻合。 通过重新选定动态不平顺性评价指标,将基于熵权的灰色关联度评价模型应用于对铁路单元评价中,引入熵权计算权重系数,避免主观赋权,通过计算关联度结果可判定其优劣次序。利用基于熵权法的灰色关联分析,不仅将峰值和均值两者指标结合进行轨道动态不平顺性综合评价,还具有以下优点。 (1)即使利用峰值、均值扣分评价时,扣分相同的单元根据综合评价得到关联度值能判断轨道单元实际质量不同,且结果与实际相符。 (2)提出综合评价法得到的关联度排序即单元动态不平顺性的排序,也是维修排序。排序目的是避免线路养护维修盲目性,工务部门能依据综合评价排序结果有计划进行日常维修,对轨道不平顺度越大优先进行维修,实现工务作业“干得准、干得好、干得多”的目标。 (3)综合评价法采用的数据是相应单元中各个指标中最大值,在面对繁多的检测数据时,此法能够快速对轨道动态不平顺性进行排序。而采用峰值均值扣分法需对所有检测数据对比标准进行扣分计算,根据扣分大小来判断单元动态不平顺性。有时扣分值相同的单元实际中动态不平顺不同,而根据本文提出的新评价方法,可得到单元关联度不同的结论,关联度越大,动态不平顺性越大,与实际结果一致。 提出基于熵权法的灰色关联分析铁路线路单元动态不平顺性综合评价,避免主观赋权,将各指标统一起来进行综合评价,为线路质量评价提供了一种可行的方法。旨在为工务维修寻求一种新的线路设备管理模式,重新构建科学的养护维修体系,通过检测监控、分析决策、计划组织、质量控制提高维修的有效性,将有限的人力、物力、财力和精力投入到重点、薄弱单元,有的放矢,避免浪费和无用功,从而使管内设备有序可控。

3.2 综合评价

4 结论
