铁路路基桩板结构荷载扩散模式及有限元计算方法研究

徐玉龙,曾长贤,郭建湖,陈尚勇

(中铁第四勘察设计院集团有限公司,武汉 430063)

高速铁路路基工程工后沉降要求高，一般地段工后沉降要求不小于15 mm[1]，地质条件复杂地段需采用特殊地基加固措施方可满足要求。桩板结构采用钢筋混凝土结构，具有优越的刚性特征，在软土[2]、岩溶、采空区[3]、交叉工程[4]等地质条件复杂地区使用可有效控制工后沉降，取得了良好的效果，尤其在桥隧相接的短路基处，桩板结构拥有和桥、隧结构相媲美的刚度，可使高速列车在桥、隧连接处平顺通过。

路基工程设计中，需对桩板结构开展结构设计，反复计算结构内力与变形，以求结构最优。现行《铁路工程地基处理技术规程》[5]对桩板结构荷载多沿用桥涵结构中荷载类型及规定，但桥涵与路基结构差异大，轨道、列车产生竖向、水平向荷载经由路基基床结构扩散到桩板结构上的模式多未明确，且路基桩板结构属“上软下硬”双层结构体系，当前成熟的“上硬下软”地层结构扩散角已不再适用，诸此种种均有待研究确定。

桩板结构属多次超静定结构，设计计算多借助于ANSYS、SAP2000等国外商业有限元计算软件。这些软件功能虽强大，但技术门槛高、使用复杂，一线设计人员使用起来较为困难，难以适应设计院高效的设计节奏。此外，成熟有限元分析软件多为国外技术垄断，存在技术壁垒，在国际科技竞争日趋白热化的今天，过度依赖国外商业软件容易埋下技术隐患。为改变这一现状，有必要基于有限元基本原理，自主编制轻便、实用的桩板结构设计软件，提高设计效率，打破技术垄断。

通过对路基桩板结构计算模型、荷载类型与扩散模式及有限元计算方法进行研究，采用Java语言和Matlab语言混合编制了桩板结构V1.0计算软件，计算方法可为结构计算提供借鉴，软件可服务于工程设计。

1 结构计算模型

桩板结构为三维结构，可简化为三维框架结构或二维框架结构，已有研究证明，两种简化模式计算结果接近，均能满足轨道控制标准要求[6]。桩板结构V1.0采用轻便的二维梁-杆模型，计算模型如图1所示，横向、纵向均取单幅板条设计计算。

图1 桩板结构二维梁-杆框架模型

桩和板均为钢筋混凝土结构，属典型梁构件，土体与桩的相互作用则可借助温克尔弹性地基理论[7]将土体简化为杆构件。一般而言，板是直接覆盖在土体上，土体对板也存在竖向支撑作用，但考虑到桩板混凝土结构与土体的刚度相差甚大，土体发生微量沉降时，就会出现桩体变形和土体变形不协调情况，板底与下部土体之间出现离层脱空，板底土体的支撑作用也就消失，故土体的竖向支撑作用不再考虑。

桩底约束方式一般为简支或固支，简支约束水平位移和竖向位移2个自由度，固支约束3个自由度，除位移外，转动也予以约束。桩底约束条件可根据桩底所在地层形式和施工工艺确定，一般桩底嵌入基岩且桩底清孔条件较好时可采用固支约束，其他情况下桩底容易发生转动，采用简支约束更符合实际。

2 设计荷载

作用在桩板结构上的荷载可分为主力和附加力，主力又进一步分为恒载和活载。桩板结构的埋置形式不同，需考虑的荷载种类也有所不同。由于轨道、列车荷载均经由基床扩散到桩板结构，首先对路基桩板结构的荷载扩散模式进行讨论，再对各类具体荷载进行研究。

2.1 “上软下硬”地层结构荷载扩散模式

路基桩板结构由路基结构和桩板结构两部分组成，两者组合后可视为双层结构体系。双层结构理论研究历史较长，从20世纪40年代已有相关研究[8]，到20世纪60年代发展出“双层体系理论”，由于应用层面较少，发展较慢，且双层结构一般只有在轴对称下才有可能获取理论解，研究多侧重于圆形荷载下的双层结构体系[9]。对于条形荷载下的平面应变问题，国内文献多引用捷克的K.E.叶戈罗夫的双层体系研究成果[10-12]，包括软弱下卧层承载力计算涉及到的双层地基条形荷载下，应力扩散所涉及的扩散角，也采用该理论解加以实验验证、简化处理后确定[13]，此后换填垫层地基处理也沿用该扩散角模式[14]。

目前，国内外应用较成熟的附加应力扩散模式主要针对“上硬下软”地层结构体系，如软弱下卧层或换填垫层设计，只规定了上下两层压缩模量比≥3的情况(Es1/Es2≥3)，虽然有研究将其扩展至上下两层压缩模量一致(Es1/Es2=1)的情况[15]，但仍局限于“上硬下软”地层结构体系。

而由于桩板结构刚性大，远大于路基基床结构，路基桩板结构属于典型“上软下硬”结构。“上软下硬”结构在条形荷载下呈现出完全不同的变化规律，压缩土层厚度h小于荷载面宽度一半(b/2)时会出现“应力集中”(图2)，即条形荷载下“上软下硬”结构界面应力峰值σz大于均质地层中界面深度的应力峰值。而“上硬下软”结构体系主要表现为“应力扩散”，即条形荷载下“上硬下软”结构界面应力峰值小于均质地层中界面深度的应力峰值。这就要求路基桩板结构的条形荷载扩散模式需重新定义。

图2 “上软下硬”地层结构在地层界面上的应力集中现象[12]

在K.E.叶戈罗夫“上软下硬”双层结构体系中，层面中点的附加应力系数主要取决于下卧层埋藏深度h与荷载跨度b之间的关系

σz=αDp

(1)

式中，σz为层面荷载中点的应力；αD为层面中点的附加应力系数；p为分布荷载。

进一步根据GB 50007—2011《建筑地基基础设计规范》所采用的附加应力系数换算扩散角方法，可换算得到不同深宽比下的扩散角。考虑桩板结构并非完全刚性，仍会发生一定变形，应力集中程度会削弱，对扩散角进一步修正，如表1所示。

表1 “上软下硬”地层界面中点附加应力系数及扩散角

通过表1可以发现，“上软下硬”地层扩散角与“上硬下软”地层的扩散角远不相同。对于浅埋式桩板结构，板结构上方仅有路基表层，厚度一般不大于0.6 m，小于荷载宽度的0.5倍，荷载扩散角度可直接取0，即荷载不发生扩散。对于深埋式板，可根据具体情况采用表1中计算扩散角，h/b介于两值之间的情况，可插值确定扩散角。h/b>2.5情况，根据K.E.叶戈罗夫研究，基本接近于均质地层的值，可根据条形荷载下均质体应力解进行计算，但建议最大不超过30°。

2.2 恒载

恒载包括结构自重、混凝土收缩和徐变影响、基础变位影响、基床表层自重、路基本体及基床底层自重和轨道结构自重。

结构自重包括桩与板的自重，为均布荷载，按均布力施加即可；混凝土收缩和徐变影响可转化为温度变化进行考虑[5]，后文再探讨温度应力问题；基础变位影响在设计中少有考虑，暂不纳入计算；基床表层自重、路基本体及基床底层自重均直接作用于板上，按板上均布力进行考虑。

轨道结构自重荷载并非直接作用在板上，而是经由基床结构传递到板上。这就涉及到条形荷载引起的附加应力问题，可采用“上软下硬”双层结构确定扩散角进行计算，如图3所示，其中，q0为线间荷载，q1为轨道荷载，线间荷载主要针对无砟轨道而言。双线情况下，由于线间荷载和轨道荷载大小不同，可在路基面先进行荷载等效后再扩散到板上。

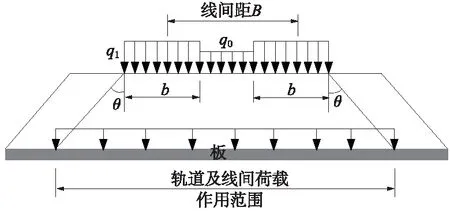
图3 轨道自重荷载扩散模式

2.3 活载

活载包括列车竖向静活载、列车竖向动力作用、离心力和横向摇摆力。

列车静活载与轨道荷载扩散形式基本相同，在双线情况下，也可先在路基面进行等效，而后按照扩散角进行扩散，如图4所示。板较宽时，扩散后荷载作用在板一定范围内，并非均布在板上。

图4 列车荷载扩散模式

高速铁路、城际铁路，顶面填土厚度≤3 m时，需考虑列车动力作用。结构计算中，动力作用可通过动力系数实现，将列车静活载乘以动力系数即可。动力系数如下式[16]

(2)

式中，Lφ为加载长度，m，桩板结构加载长度取平均跨度乘以调整系数，调整系数可将单块桩板结构视为连续梁，参照连续梁的调整系数取值(表2)；μ折减为动力系数折减系数；hc为结构顶面至路基面的填土厚度，m。

表2 跨数调整系数[16]

曲线桩板结构地段需考虑列车竖向静活载产生的离心力作用[16]。离心力为水平方向力，由于基床结构为散体材料，散体材料具有耗散性，会通过自身调整、变形吸收一部分能量，传递到板上的力可能出现大幅减小。水平力经由散体材料传递到桩板结构的机理及精确解目前尚难明确，但考虑到基床结构可提供摩擦力，水平力可借助基床结构的摩擦作用传递到桩板结构的板顶面，而摩擦力的存在是通过竖向荷载实现，当前暂推荐离心力qc采用与列车荷载相同的扩散模式及扩散角，如图5所示。

图5 离心力扩散模式

路基地基处理规程中对离心力并无明确规定，仅要求借鉴桥涵规范计算方法。在桥涵结构中，离心力计算方法为[16]

(3)

式中，C为离心率，≯0.15；f为列车竖向活载折减系数；R为曲线半径，m；W为列车荷载图式中集中荷载或分布荷载，kN或kN/m。

离心力本质上是活载在曲线上运动形成的惯性力，应用到路基工程中时，W取列车活载q2(kN/m2)即可，获得的离心力F可表示为离心荷载qc(kN/m2)。

列车运动时还会产生横向摇摆力。按横向摇摆力为集中力，大小为100 kN，只考虑1个股道摇摆力[5]。计算时，将横向摇摆力在轨道板范围内进行均布，再扩散传递到板结构上，如图6所示。进行荷载组合时，需将摇摆力Qns分别放在左线和右线进行计算，选择最不利组合。

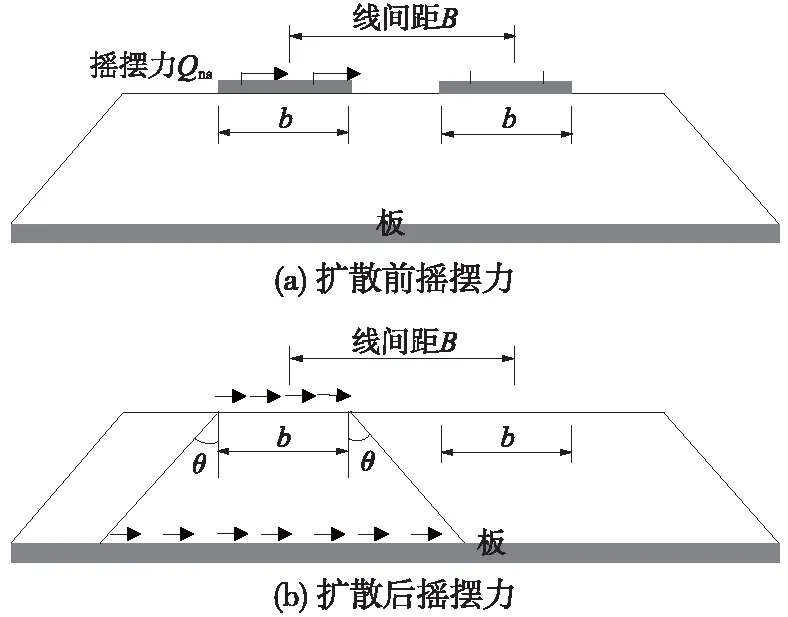
图6 摇摆力扩散模式

2.4 附加力

附加力主要有制动力或牵引力和温度变化影响。

制动力或牵引力作用方向为线路方向，在计算桩板结构纵向板条时需考虑，作用方向水平，制动力或牵引力大小取列车竖向静活载的10%计算。由于制动力或牵引力经由轨道传递到路基结构，轨道长度一般远大于桩板结构单块板长，制动力或牵引力作用范围分布在整个纵向板条。当与列车竖向动力作用同时计算时，制动力或牵引力应按列车竖向静活载的7%计算[5]。

温度变化影响为结构在均匀温差和日照温差引起的变形和应力。桩板结构可参照涵洞规定，对于涵洞，最冷月平均气温不低于-20 ℃时，气温变化影响可不考虑[16]。当温差过大时，结构需考虑这种温度变化效应。

3 有限元计算方法

3.1 单元形式

桩板结构简化为二维框架结构后，有限元计算中涉及到的单元形式主要有杆单元和梁单元。土弹簧采用杆单元，桩与梁分别采用2种力学参数不同的梁单元。杆单元的划分较为简单，可直接取每根杆件作为一个单元，梁单元则要设定单元大小后划分成若干单元。

3.1.1 杆单元

杆单元采用二力杆，位移函数采用2个待定常数，局部坐标系下表达式为[17]

(4)

式中，u(x)为杆单元水平位移；ui、uj为杆单元两端节点位移；l为杆单元长度；x为i为原点，沿ij方向坐标；[N]为形函数。杆单元本构关系为

(5)

局部坐标系下杆单元刚度矩阵为

(6)

式中，E为杆弹性模量；A为杆截面积。

桩板结构中，土体与桩体之间的接触作用通常采用弹性地基理论的“m法”或“k法”，转化为弹性力学中的杆单元需一定转换关系。杆单元弹性模量E=mhL或E=kL，h为埋深，“m法”或“k法”可结合支挡工程相关规范确定[18]。其中，L为杆件长度，可按L=1 m设置。单个弹簧作用面积为相邻单元的平均长度与桩有效宽度之积。

A=b0(li+li+1)/2

(7)

式中，A为单个弹簧作用面积，对应杆单元截面积；li与li+1为弹簧节点连接的两个相邻桩单元长度，b0为桩单元有效宽度，可根据桩基规范[19]确定。

设计中经常出现板伸入路基本体中情况，采用“m法”计算弹性模量时，需确定深度h的计算零点。考虑到路基本体并非大面积填土[13]，并不能提高路基侧向约束，故计算零点从地面起较合适。但路基本体填料具有较高的压实性，也能够提供一定侧向约束，与桩体形成接触关系。如此，可假设路基本体层厚度为h0，在路基本体层，深度计算零点从板开始算起，k=-m0y，m0为路基本体的水平抗力系数的比例系数；而地面以下土层，深度计算零点从地面开始，k=-m(y-h0)，如图7所示。

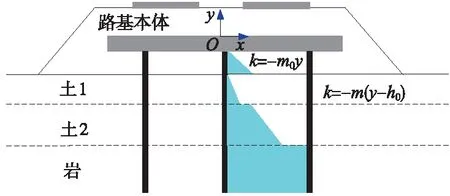
图7 埋置于路基本体的桩板结构水平抗力示意

3.1.2 梁单元

梁单元也采用两节点模型构造，形函数矩阵[Nv]和单刚矩阵[k]e如下

[Nv]=

(8)

单元刚度矩阵

(9)

式中，l为单元长度；A为截面积；EI为抗弯刚度；I为惯性矩。

桩和板结构均可简化为梁单元，截面积A和惯性矩I按材料力学确定[20]。板结构弹性模量根据混凝土强度等级确定即可，但桩简化为梁单元时，抗弯刚度EI建议参照《铁路桥涵混凝土结构设计规范》[21]确定，对于钢筋混凝土桩，EI=0.8EcI，其中，Ec为混凝土弹性模量，I为桩身截面惯性矩。

3.2 荷载等效

荷载通过等效节点力的形式施加到单元节点。等效节点力是根据功互等原理，将分布载荷转移到节点上所得到的载荷。对于均布荷载作用下桩板结构的梁单元(图8)，每个单元在局部坐标系下的等效节点力为

(10)

式中，p为水平方向均布荷载；q为竖直方向均布荷载；l为单元长度。

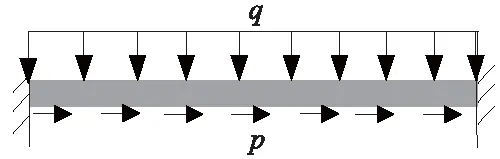
图8 均布荷载下梁单元等效节点荷载

桩板结构中需计算温度变化引起的变形和内力，混凝土徐变也借助温度变形来实现。桩板结构温度变化引起的应力变形属于稳态热传导问题，也可采用等效节点荷载进行计算[22]。温度荷载内力表达式如下

(11)

式中，E为单元弹性模量；A为单元截面积；αtemp为混凝土线膨胀系数；ΔT为温度变化量。

温度引起的变形和内力只考虑梁与板，杆单元可不予考虑。

3.3 计算流程

整个计算流程分为前处理、有限元计算和后处理，如图9所示。前处理主要通过Java Swing模块编制输入界面，有限元计算采用Matlab软件编制，后处理可输出内力图和计算书等。

图9 桩板结构软件计算流程

有限元计算部分流程为[17]：(1)建立计算模型(结构离散化、划分单元、节点编号等)；(2)计算单元刚度矩阵和单元的节点力列阵；(3)形成整体刚度矩阵；(4)计算整体节点力；(5)引入位移边界条件；(6)求解整体平衡方程；(7)回代求解单元内力。

4 案例分析

下面采用桩板结构V1.0与商业有限元软件对典型案例的计算运算结果进行对比。

假设浅埋式桩板结构，板宽度15 m，板条纵向单幅长5 m，板厚0.8 m。桩间距5 m，两端悬挑2.5 m，共3根桩，桩长15，8，3 m，桩径0.8 m，桩底均为固支条件。

轨道结构采用Ⅲ型板，轨道分布宽度b=3.1 m，轨道自重q1=13.7 kPa，列车荷载q2=40.4 kPa，线间距b0=5 m，线间荷载q0=2.3 kPa。基床表层厚度0.4 m，计算得到扩散角为0°。水平荷载考虑摇摆力100 kN作用在整个板上，单幅作用力按25 kN计，分布区间[-4.05 m，-0.95 m]，分布力为8.1 kN/m。计算考虑徐变影响，通过设定板与桩温度均下降15 ℃实现。桩与板均采用C35混凝土，弹性模量均为31.5 Pa。地层参数如表3所示。

表3 地层参数

计算时，桩与板单元网格长度0.5 m，杆单元网格长度1 m。

采用桩板结构V1.0计算得到弯矩如图10(a)所示。板上最大弯矩为535 kN·m，最小弯矩为-669.5 kN·m。桩上最大弯矩106.3 kN·m，最小弯矩-22.7 kN·m，其中，下缘纤维受拉、上缘纤维受压时弯矩为正。采用商业有限元软件计算的弯矩如图10(b)所示。对比发现，采用桩板结构V1.0计算得到弯矩最大值、最小值及弯矩形态与商业软件获取值是一致的。

除内力外，采用桩板结构V1.0计算得到的节点位移也与商业软件获取的位移存在较好的吻合，见表4，说明桩板结构V1.0有限元算法是正确的。

图10 弯矩对比

5 结语

对路基工程中常用的桩板结构计算模型、荷载扩散模式、有限元计算方法进行了研究，主要结论如下。

(1)借助温克尔弹性地基梁理论，桩板结构可简化为二维梁-杆框架结构，便于有限元计算。

(2)针对路基基床结构与桩板结构组成的“上软下硬”双层地基结构体系，面荷载作用下，分界面会出现应力集中现象，路基荷载扩散至桩板结构上的扩散角与深宽比存在一定关系，整体上位于0～30°范围内。研究弥补了现行路基规范中对桩板结构荷载规定过于模糊的问题。

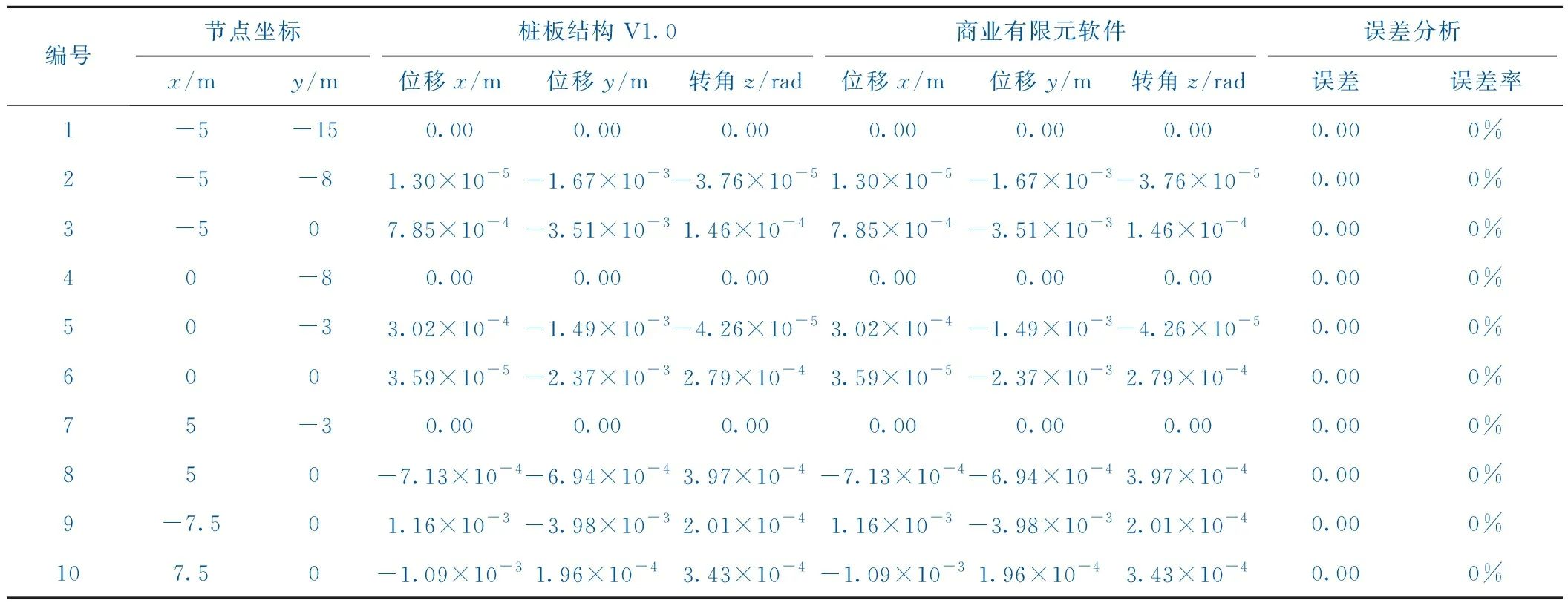
表4 代表性节点位移比较

(3)构建了有限元理论框架下的梁、杆单元刚度矩阵与温度等效荷载，自主编制了桩板结构V1.0结构计算软件。对比商业有限元软件与自编软件的计算结果，显示两者具有良好的吻合性，桩板结构V1.0可服务于工程设计优化。

实践证明，自编桩板结构V1.0软件可高效应用于铁路设计中，但也存在一定不足。当前梁单元仍采用常用的Euler梁，由于桩板结构跨度较小，采用考虑剪切变形的Timoshenko梁更为合适。同时，随着异形结构的发展，桩板结构中桩排列方式并不完全规则对称，简化为二维框架结构存在误差较大问题，三维桩板结构计算软件的实现也迫在眉睫。