基于改进长短期记忆网络的时间序列预测研究

陈孝文,苏 攀,吴彬溶,成 承,王 林

(1.湖北中烟工业有限责任公司，湖北 武汉 430040;2.华中科技大学 管理学院，湖北 武汉 430074)

准确的时间序列预测有助于管理者提前做好布局和决策，所以时间序列预测得到了广泛的关注和应用，例如共享单车租赁需求预测[1]、汇率预测[2]、客运量预测[3]、期货价格预测[4]等领域。时间序列数据可以描述为一组按时间顺序的观察结果，类型可以分为单变量时间序列和多变量时间序列，具有数据规模大、维度高等特点。时间序列预测问题采用的模型大致分为经典统计模型(ARIMA、VAR模型)和机器学习模型(如支持向量机、人工神经网络模型)[5]。经典统计模型通过研究时间数据的演化，预测未来的走势。机器学习模型具有强大的非线性拟合能力，近年来也被广泛应用到时间序列预测中。随着大数据时代的到来，多变量、多通道的海量时间序列数据呈爆炸式增长，多元时间序列数据具有高维和时空相关性特征，或包含噪声数据，使经典统计方法难以有效建模。此外，传统的方法在处理大数据，特别是海量、复杂的多变量时态数据时也存在局限性。而深度学习模型具有较强的自适应能力、灵活的非线性建模能力以及海量的学习和并行计算能力，是求解复杂非线性系统的有效方法[6]。因此，数据驱动的深度学习预测方法越来越受到研究者的青睐。

作为常用的深度学习模型之一，长短期记忆网络(long short-term memory，LSTM)能够分析长跨度的时间序列并预测，有效解决传统循环神经网络梯度消失的问题。目前，LSTM已被广泛应用于文本识别、语音识别、疾病诊断、时间序列预测等多个领域[7-8]。为研究更加高效、精确的时间序列预测模型，笔者将基于注意机制的双向LSTM应用于时间序列预测。双向机制可以从顺序和逆序充分挖掘输入变量的有效信息，防止长输入时的部分前段输入信息的缺失[9]。同时，通过注意力机制，对不同的输入变量赋予不同的权重，从而LSTM可以突出更关键的影响因素[10]。目前国内外已有研究使用注意力机制或双向机制优化LSMT，比如高华睿等[8]使用考虑注意力机制的双向长短时记忆神经网络，应用于预测高速公路短时交通流，并取得了不错的效果；PENG等[10]使用了基于注意力机制的LSTM预测国内外能源消耗量，进一步证实注意力机制给LSTM模型带来的性能提升。然而，LSTM的许多参数都会影响预测性能，但确定合适的参数组合通常是困难的。因此，笔者采用带有外部归档的自适应差分进化算法(adaptive differential evolution with optional external archive，JADE)确定LSTM的超参数。

目前很多时间序列预测研究都是基于数据分解方法的，比如奇异谱分析、变分模态分解、经验模态分解和集合经验模态分解等。数据分解方法有助于去除原始时间序列的随机干扰，提高时间序列预测的性能。变分模态分解(variational mode decomposition，VMD)作为一种新的信号分解方法，在大部分情况下其分解性能都优于基于经验模态分解和奇异谱分析等分解技术，能更充分地分解原始信号[11]。因此，笔者在时间预测框架中引入了VMD。

通过两个数值算例验证了所提出VMD-JADE-基于注意力的双向LSTM模型的可行性。实证结果表明，与其他常用方法相比，VMD-JADE-基于注意力的双向LSTM模型可以提高时间序列预测的准确性。主要贡献如下：①通过人工智能技术，提出了一种有效且新颖的时间序列预测模型，即VMD-JADE-基于注意力的双向LSTM模型，该模型结合了VMD的降噪能力、注意力机制的关键信息捕获能力、双向机制的输入变量的信息提取能力、JADE的智能高效搜索参数能力和LSTM对时间序列的精确预测能力。②利用注意力机制的权重对分解后的子序列和其他多元输入变量的重要性进行了评估。从而识别时间序列预测中的重要变量，为决策者提供有说服力的时间序列预测分析和决策支持。

1 研究设计的预测框架

VMD-JADE-基于注意力机制的双向LSTM模型的预测框架如图1所示。在VMD-JADE-基于注意力机制的双向LSTM的预测框架中，VMD将原始时间序列数据分解为若干个子序列，JADE对基于注意力机制的双向LSTM的几个关键参数进行优化，再将子序列和其他相关影响因素输入到改进的LSTM中进行预测。VMD-JADE-基于注意力机制的双向LSTM模型结合了VMD、JADE和基于注意力机制的双向LSTM的优点。最后使用VMD-JADE-基于注意力机制的双向LSTM模型对单因素每日纸浆期货价格及多因素每周玉米期货价格进行预测，并使用注意力权重分析每个预测算子的重要性。下面将详细介绍使用VMD、JADE和基于注意力机制的双向LSTM。

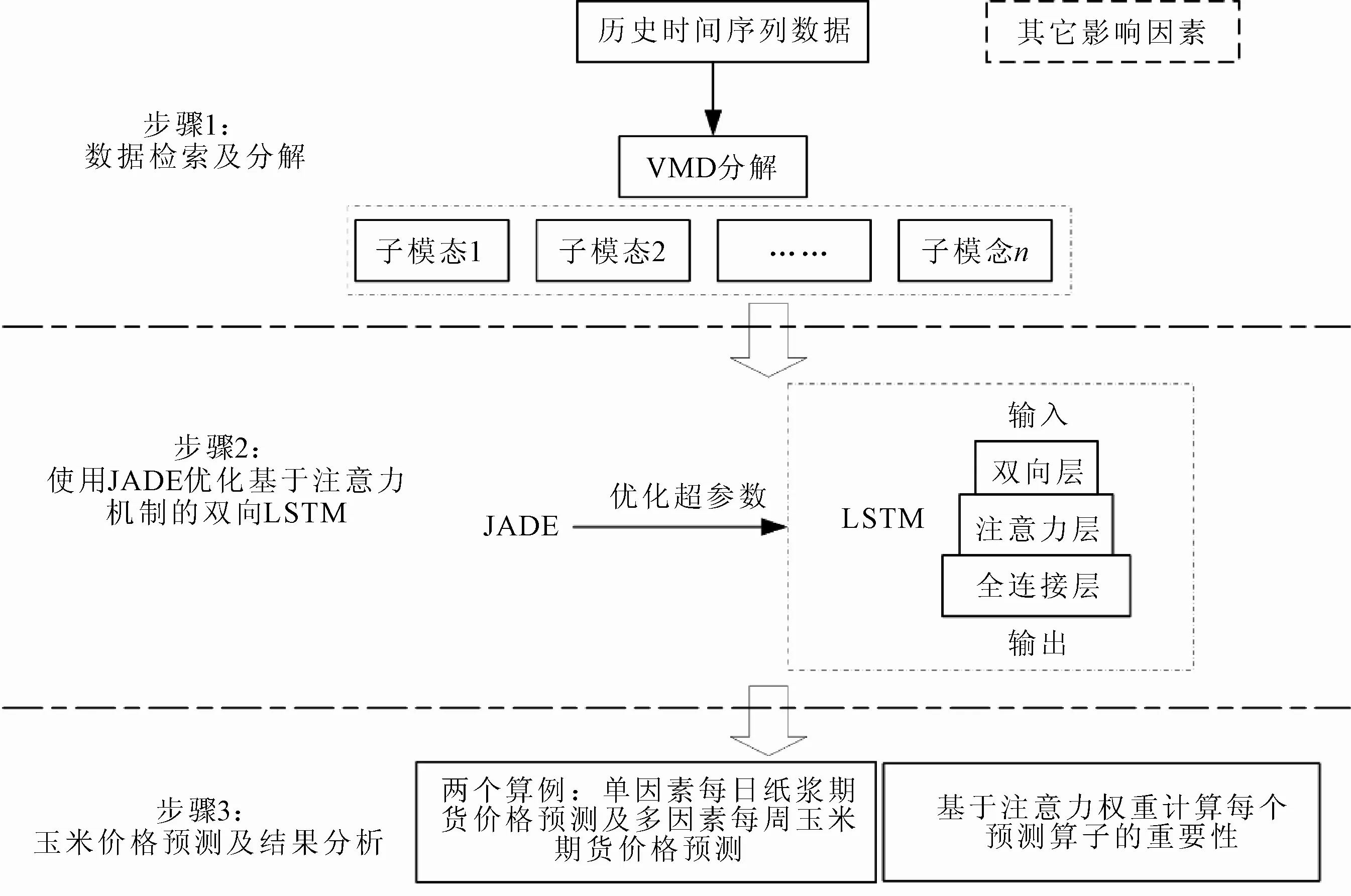
图1 VMD-JADE-基于注意力机制的双向LSTM模型的预测框架图

(1)变分模态分解VMD。VMD是一种非递归的、自适应的信号处理方法，对非线性和非平稳信号有很好的处理效果，也可用于确定时间序列的周期性。VMD将实信号分解为有限数量的子信号，称为分量，这些分量被认为是紧凑围绕相应中心频率的。VMD的优点是在处理数据噪声和分解时序数据时稳健、高效。对历史时间序列进行分解，分解后的子序列再输入到预测模型中，有利于筛选子序列中的无用信息，以此提升时间序列预测的精确度。

在分解技术中，基于EMD和基于WT的方法应用最为广泛。基于EMD的技术是自适应的，需要调整的参数更少，对噪声和采样更敏感，更容易分解，但分解的不够充分。基于WT的方法在时域和频域具有突出的局部化特性，但是其性能在很大程度上取决于分解层数和分解二叉树的结构。相比之下，VMD由于具有较强的数学理论基础[12]，可以实现信号的精确分离，具有较高的计算性能。相关实验表明，VMD技术的分解性能优于基于EMD和基于WT的分解技术[13]。VMD能够将原始时间序列数据充分分解成若干个子序列，最大限度地降低由于原始序列波动性大、随机性强而导致的预测难度。同时，LSTM可以很好地选择对预测贡献较大的子序列。因此，笔者利用VMD对原始时间序列数据进行分解。

VMD分解中最重要的一步就是确定分解子序列的具体数目，如果子模态数量少，则原始序列可能不能被完全分解，导致预测不准确。如果信号被过度分解，那么子模态之间的差异就会变得非常小，增加了不必要的计算开销。利用剩余能量的比例rres来确定VMD输出的适当数量。rres的公式如下:

(1)

式中：f(t)为原始时间序列数据；Ns为样本数;K为分解的子模态数量；uk(t)为已分解的模式。rres小于百分之三且没有明显的下降趋势，则可以确定最佳的子模态数量[14]。

(2)带有外部归档的自适应差分进化算法JADE。DE算法是一种常用的智能优化算法，具有实现简单、效率高的优点[15]。大量研究表明，DE在很多问题上都优于其他常用算法，例如全局优化问题[16]。ZHANG等[17]提出的JADE是一种具有可选外部存档的自适应差分进化算法。仿真结果表明，在大多数情况下，JADE算法的收敛性能优于其他自适应DE算法。JADE作为DE的变体之一，具有更好的全局搜索能力和搜索效率。因此，笔者使用JADE优化的LSTM。

利用JADE确定基于注意力机制的双向LSTM的参数。所选参数为时间步长、隐藏层神经元个数、批量大小和迭代次数。JADE是DE算法的一个极好的变体，在高维问题上显示了极好的结果。与基本的DE相比，JADE有3个主要的改进：①实现了新的“DE/current-to-pbest”突变策略；②增加了一个可选的外部存档；③参数自适应更新。“DE/current-to-pbest”和可选的归档操作可以分散存储空间，提高收敛性能。参数自适应将控制参数自动更新到合适的值，提高了算法的鲁棒性。

(3)基于注意力机制的双向LSTM。HOCHREITER等[18]提出了长短期神经网络LSTM。LSTM是一种RNN变体，用于解决简单RNN的长期记忆不足，特有的门控机制使其拥有持久化的信息类型、持久化的持续时间以及从存储单元读取信息日期的能力。因此，LSTM可以保留输入信号中的重要信息，忽略不太重要的分量。这个存储单元有一个递归的自连接线性单元，称为“常量误差传递”，可以长时间维护依赖关系。因此，与简单的RNN相比，LSTM在网络中保留了信息并传播了更长链的误差，从而克服了梯度消失的问题。

笔者使用基于注意力机制的双向LSTM作为可靠高效的预测模型，其结构如图2所示。双向LSTM即指同时考虑输入的顺序序列和逆序序列，因输入序列过长时预测模型更偏向输入末端的信息而忽视了前段的有效信息，导致部分输入信息的缺失，而双向LSTM可以很好地解决这个问题，从而提升LSTM模型的特征提取能力和预测能力。双向LSTM包含前向LSTMF(Forward LSTM)和后向LSTMB(Backward LSTM)。在每一层时间维度上，将双向LSMT的输入分别用两个相反方向的LSTM处理，随后将两个LSMT的最终输入连接在一起作为下一层的输入。双向LSTM的传递机制如下：

Ft=f(w1xt+w2Ft-1)

(2)

(3)

(4)

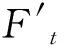
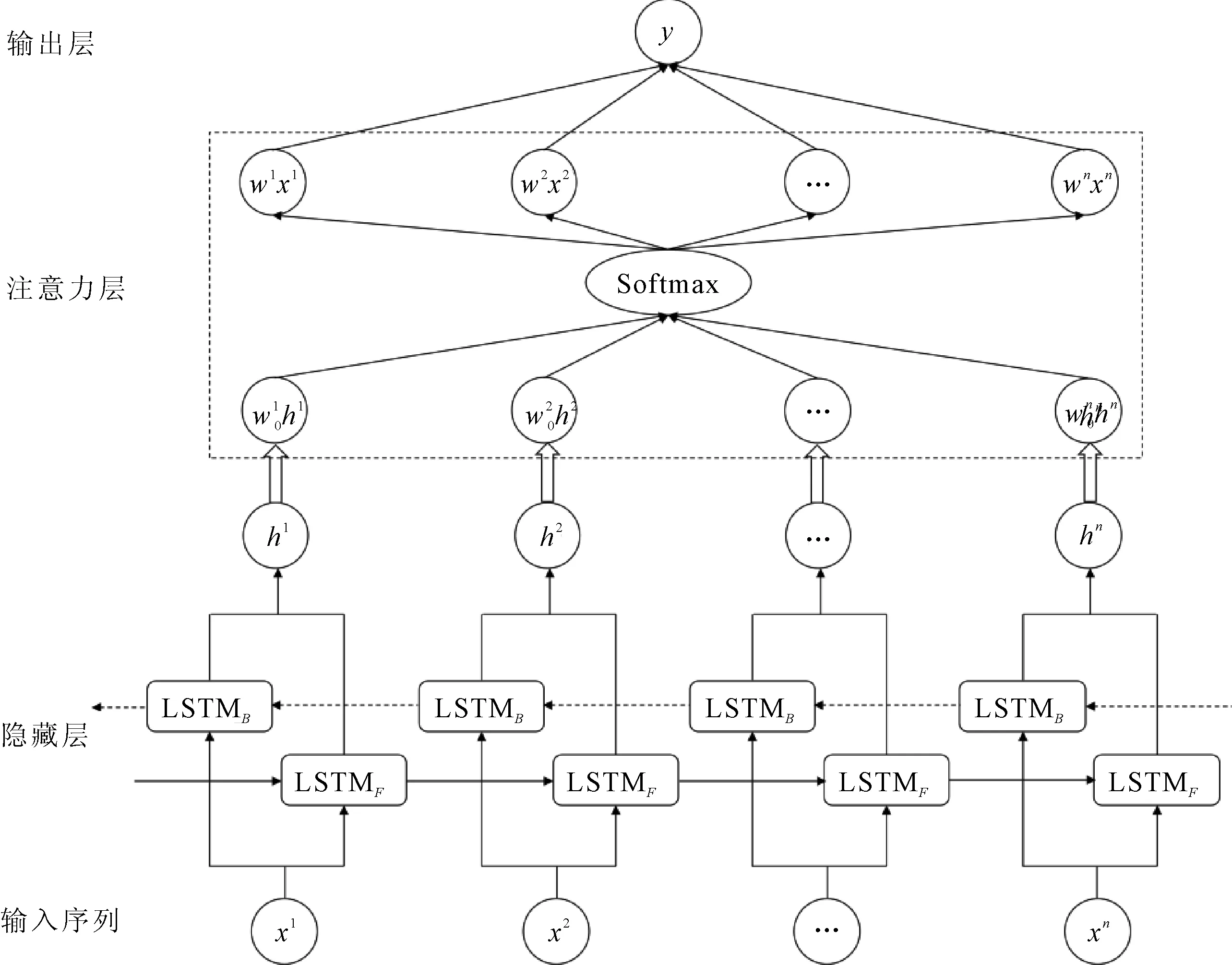
图2 基于注意力机制的双向LSTM的结构图

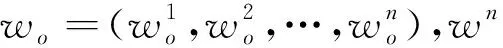
双向机制可以从顺序和逆序两个方向挖掘输入变量的重要信息，注意机制通过对输入的特征赋予不同的权重来捕获重要的因素，因此，结合了注意机制和双向机制的优点，设计基于注意力机制的双向LSTM。

2 应用案例与结果分析

2.1 实例一：单因素纸浆期货价格预测

2.1.1 数据集及数据预处理

受新冠疫情、国际局势、供求关系等多重因素影响，2020年11月—2022年3月纸浆价格波动剧烈，对下游造纸企业及供应链下游企业(如烟草企业白卡纸的采购)等产生了较大冲击。基于此，准确地预测纸浆价格对于下游企业的采购、库存等决策至关重要。

每日纸浆期货价格来自于“英为财情”(www.investing.com)，全称为漂白针叶木硫酸盐纸浆(bleached softwood kraft pulp futures，SSPK2)，时间跨度为2020年9月1日—2022年3月25日。训练集为2020年9月1日—2021年12月31日，共325个交易日数据；验证集为2022年1月1日—2022年2月28日，共35个交易日数据；测试集为2022年3月1日—2022年3月25日，共19个交易日数据。训练集用来训练模型，验证集用来调整参数，测试集用来测试预测模型的性能。纸浆价格走势如图3所示。

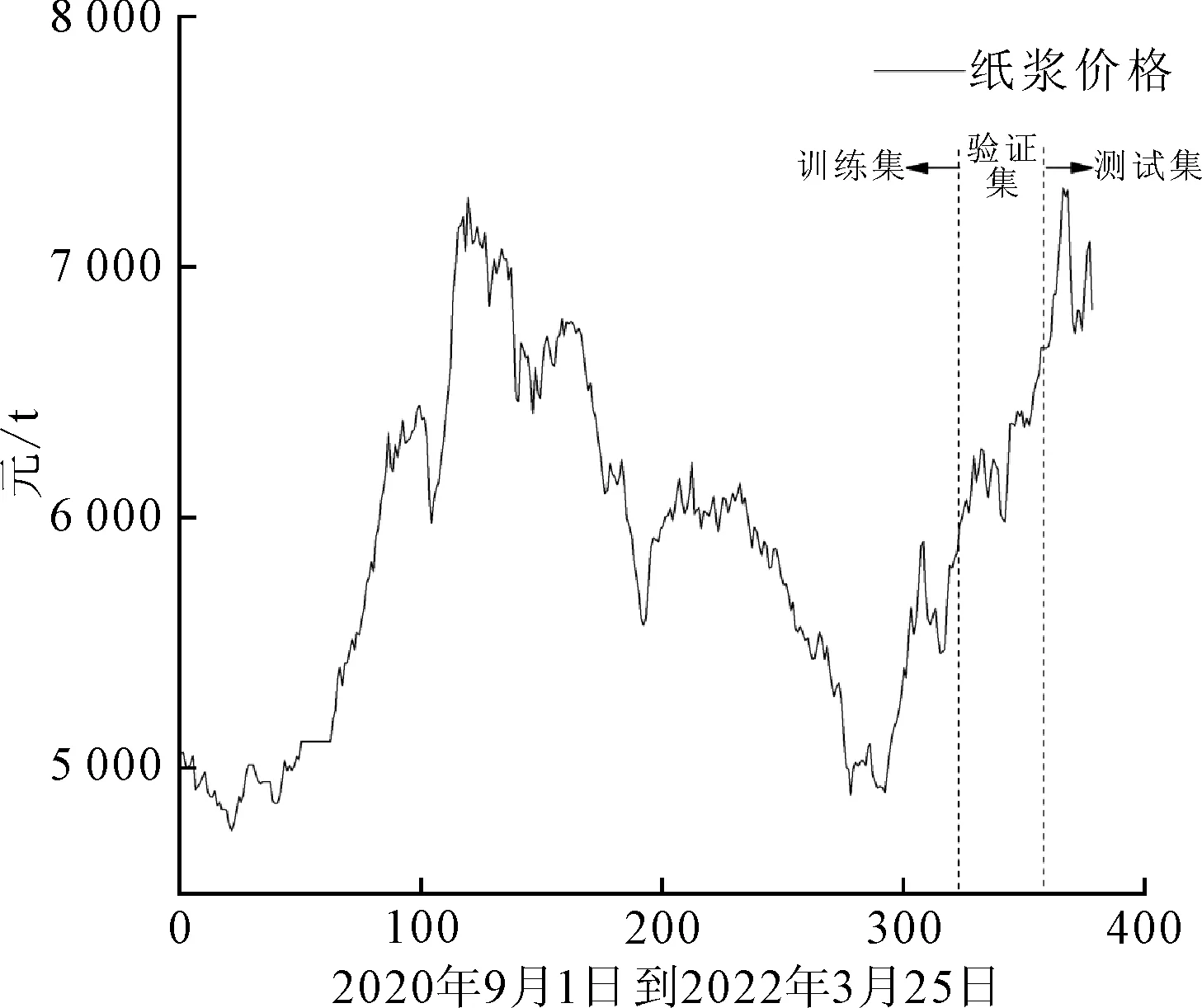
图3 纸浆价格走势图

2.1.2 预测性能评估指标

利用两个尺度相关误差(MAE和RMSE)和一个百分比误差(MAPE)评估模型的预测性能，3个指标的计算方法如下：

(5)

(6)

(7)

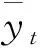
2.1.3 对比模型及参数设置

为验证所提出的预测模型的稳定性和准确性，将其与长短期神经网络、循环神经网络、门控循环单元、反向传播神经网络、DE-基于注意力机制的双向LSTM、JADE-基于注意力机制的LSTM、JADE-双向LSTM、EMD-JADE-基于注意力机制的双向LSTM进行比较。其中，长短期神经网络、循环神经网络、门控循环单元、反向传播神经网络是常用的时间序列预测模型[20]。为了对比JADE算法在搜索参数时的优越性，采用DE和JADE作为不同的智能优化算法，对基于注意力机制的双向LSTM模型的参数进行搜索。此外，笔者比较了VMD与其他分解方法的分解效果，即使用经验模态分解(EMD)处理原时间序列数据，并输入到预测模型中与VMD分解后输入到预测模型中的结果进行对比。

利用VMD将原始时间序列数据分解为数个子模态，以减少原始数据的非平稳特性。合适的子模态数目可以由剩余能量的比值rres来确定，不同子模态数量时rres的值如表1所示。当子模态数目为5时rres值小于3%且无明显下降趋势，说明其为最合适的分解数量。分解后的纸浆价格子序列如图4所示，相对低频的子模态代表了原始纸浆价格的总体趋势；中频的子模态表示纸浆价格的局部波动趋势；高频的子模态表示纸浆价格序列的残差。提取的中低频子序列比原始数据更加平滑，有利于提高纸浆价格预测性能。

表1 不同子模态数量对应的rres值

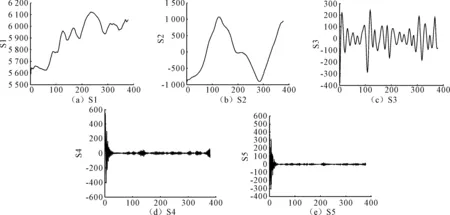
图4 VMD分解后的纸浆价格子序列

采用高效、简单的网格搜索方法对DE、JADE的参数进行优化。这些进化算法随后被用来寻找所提出模型的最优参数。基于注意力机制的双向LSMT的参数搜索范围为：时间步长数的范围为[2,10];批量数量范围为[16,64];迭代次数为[100,500];隐藏层神经元数量范围为[2,32]。经过JADE搜索得到的所提出模型的最佳参数组合为：时间步长为4，批量大小为51，迭代次数为432，隐藏层神经元数量为15。

2.1.4 预测结果和讨论

使用MAPE、MAE和RMSE对VMD-JADE-基于注意力机制的双向LSTM模型的预测结果与其他预测方法进行比较，各模型的预测结果如表2所示。测试集上各模型的预测值与真实值的拟合情况如图5所示。可知JADE-基于注意力机制的双向LSTM模型的结果更贴近真实值。与其他模型相比，VMD-JADE-基于注意力机制的双向LSTM模型在3个指标上都取得了最佳的表现。JADE优化后的LSTM模型的预测性能比DE优化后的LSTM的预测模型就MAPE而言降低了14.10%，说明JADE在寻找LSTM模型的最佳参数组合时优于基本的DE算法，进一步证明了JADE算法的高效性。VMD分解后的子序列输入到所提出的预测模型中比EMD分解输入到预测模型的结果就MAPE而言降低了20.24%，说明VMD比EMD分解原始序列更加充分，更适用于时间序列预测的分解和降噪。

表2 不同模型的预测结果

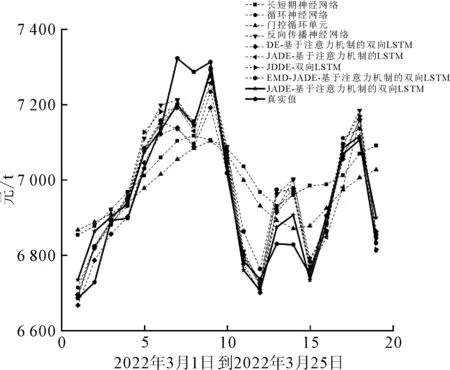
图5 各模型预测值与真实值的拟合情况

滞后阶数为1时的S1～S5的注意力权重如图6所示。注意力权重表示注意力层计算时各个神经元的参数值，反映了输入变量在纸浆价格预测中的作用，权重越大，在预测中发挥的作用越大。可知，S1～S3对于纸浆价格预测的贡献较大，而S4和S5在预测中发挥的作用较小。分解的频率越低，越能反映纸浆价格的大致趋势，分解频率适中可以很好反映纸浆价格的拐点，也在预测中发挥了重要作用，而高频序列如S4和S5则包含了较大噪音，所以在纸浆价格预测中发挥的作用偏低。

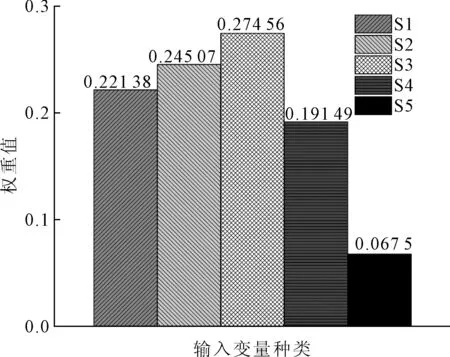
图6 输入变量的注意力权重值

2.2 实例二：多因素玉米期货价格预测

受新冠疫情、国际政治局势、国内供求关系、大宗商品上涨等因素的影响，近年来我国玉米期货价格波动幅度较大，而准确的玉米期货价格预测不仅有助于国内农产品基准价格定价，发挥期货市场的调节作用，也有助于种植业、农产品加工业及生猪养殖业的良性发展。参考近年来玉米期货价格研究文献[19]，笔者综合考虑了玉米价格的历史波动趋势、供求关系、国际影响方面的因素，构建影响因子指标，如表3所示，时间跨度为2019年1月4日—2022年3月25日，共164个交易周数据。其中，训练集为2019年1月7日—2021年10月31日，共144个交易周数据；验证集为2021年11月1日—2021年12月31日，共9个交易周数据；测试集为2022年1月1日—2022年3月25日，共11个交易周数据。

为清晰地展示中国玉米期货价格与其他输入变量之间的关系，将各指标线性缩放至0.1～0.9之间，如图7所示,中国玉米期货价格与其他输入变量的波动具有一定的相似性或滞后性，说明选中的其他输入指标对玉米期货价格有一定的影响，可用于玉米期货价格的预测研究。

算例二的对比模型和进化算法的搜索范围都与算例一相同。不同子模态数下对应的rres值如表4所示。由表可知，当子模态数目为7时rres小于3%且无明显下降趋势，说明其为最合适的分解数量。受篇幅限制，VMD分解后的子序列图不做展示。经过JADE搜索所提出模型的最佳参数组合为：时间步长为3，批量大小为43，迭代次数为312，隐藏层神经元数量为19。

表4 算例二中不同子模态数量对应的rres值

利用多因素玉米期货价格数据验证VMD-JADE-基于注意力机制的双向LSTM模型的可行性和有效性，不同模型的预测结果如表5所示，各模型预测值与真实值的拟合情况如图8所示，所提出模型在所有使用的模型中取得了最佳的预测性能，其预测值与实际值最为贴合，证明了所提出模型的精准性。对比所提出模型与DE-基于注意力机制的双向LSTM，所提出模型较DE-基于注意力机制的双向LSTM模型的MAPE、MAE、RMSE分别改善了58.62%、58.78%和66.42%，证明了JADE算法在搜索神经网络最佳参数组合时的优越性。实验结果还表明只考虑单一的改善LSTM的方法，即JADE-基于注意力机制的LSTM或JADE-双向LSTM，虽然较基础的LSTM取得一定的改进，但综合两者优势的JADE-基于注意力机制的双向LSTM表现更加突出。

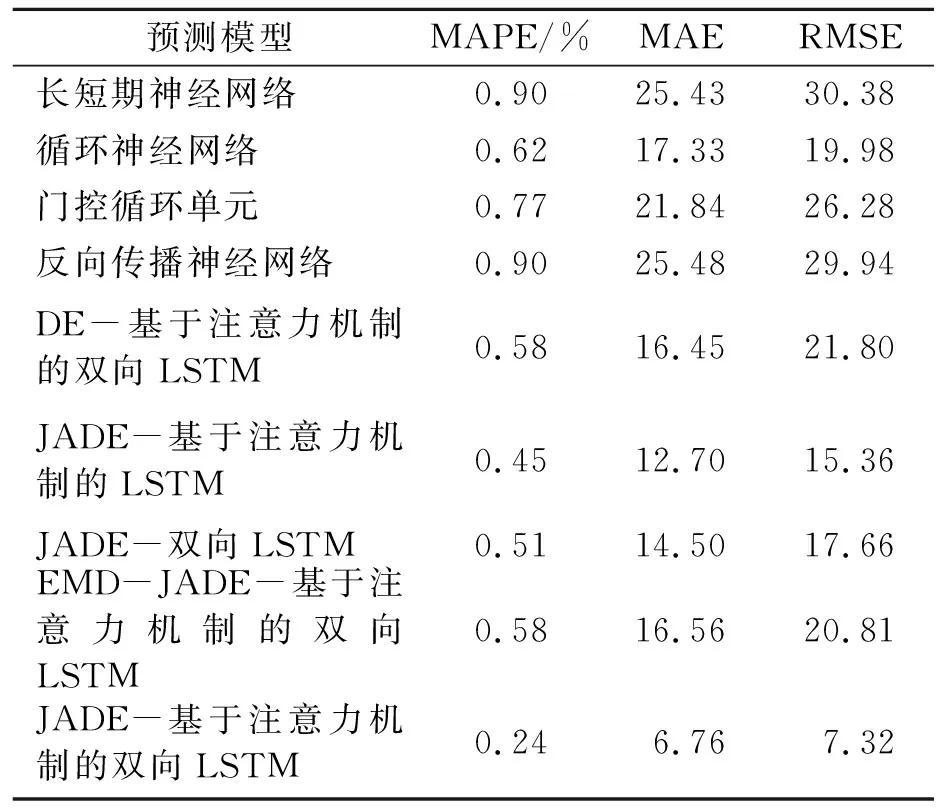
表5 不同模型的预测结果

输入变量的注意力权重值及各个输入变量在玉米期货价格中发挥的作用图9所示。可知，S1、国际玉米期货价格、S4、国际原油期货价格和生猪价格指数分别为对价格预测影响最大的5个输入变量，说明VMD分解的低频序列能很好地反映原始数据波动的大致趋势，中频序列能很好地反映原始数据的拐点，都对时间序列的预测产生较大作用；国际玉米期货价格、国际原油期货价格和生猪价格指数的变化对我国玉米期货价格都有较大的冲击，因为其反映国际环境、供求关系等我国玉米期货的影响。

图9 算例二中的输入变量的注意力权重值

3 结论

笔者提出了一种基于数据分解、注意力机制、双向机制、JADE算法优化超参数的改进LSMT模型。注意力机制可以捕获关键信息，提高多因素预测的准确性，双向机制可以从顺序序列和逆序序列两个方向充分挖掘数据特征，防止部分前段有效信息的丢失。以单因素纸浆价格预测和多因素玉米期货价格预测为例，验证了所提出的VMD-JADE-基于注意力机制的双向LSTM模型的有效性和优越性。结果表明，VMD-JADE-基于注意力机制的双向LSTM模型效果优于其它对比模型，且通过分析注意力权重能够给输入变量进行重要性排序，能够为管理者提供决策支持，所提出的方法适用于时间序列预测。

模型也存在一定的局限性。首先，仅考虑了单个分解模型的效果，二次分解模型也可用于时间序列分解，能否取得更好的分解效果尚需进一步研究。其次，多目标优化算法或者其他智能算法，如果蝇优化算法和鲸鱼优化算法，也可以用于识别合适的LSTM参数组合。