考虑多时段设备耦合的数据中心能效优化方法

高晋坤，余 娟，刘珏麟，杨知方，谢永胜，徐 森

（1. 输配电装备及系统安全与新技术国家重点实验室（重庆大学）,重庆市 400044；2. 国网新疆电力有限公司,新疆维吾尔自治区乌鲁木齐市 830011）

0 引言

在“双碳”目标的指引下,绿色、低碳、节能降耗已逐渐成为全社会共识［1-2］。当前,随着云计算和人工智能（AI）等技术的广泛应用,数据中心作为信息技术（IT）的核心基础设施［3］,其规模也在不断扩大。中国数据中心的规模自2013 年以来快速增长,截至2020 年底,在用数据中心机架总规模已达到395 万架,年均增速超过30%［4］。然而,其高能耗问题也日益受到关注［5-6］。2020 年,全国数据中心的总耗电量为204.5 TW·h,约占社会总耗电量的2.7%,是当年三峡大坝发电量的1.83 倍；预计到2025 年,全国数据中心总耗电量将达到395.2 TW·h,约占社会总耗电量的4.1%［7］。

电能使用效率（power usage effectiveness,PUE）是数据中心总设备能耗与IT 设备总能耗的比值,作为衡量数据中心能耗效率的核心指标,其值越小越好。目前,中国数据中心的PUE 值普遍为1.5～2.0,距离国际先进水平（1.0～1.5）仍有较大差距［7］。节能降耗是中国可持续发展的基本国策之一。数据中心巨大的能源消耗,不利于节能型社会的创建和“双碳”目标的实现。2021 年5 月,国家发展和改革委员会、中共中央网络安全和信息化委员会办公室、工业和信息化部以及国家能源局联合发布的全国一体化大数据中心协同创新体系算力枢纽实施方案中,明确要求加快技术研发应用,实现数据中心节能降耗。因此,亟须提高数据中心的能源使用效率,实现绿色可持续发展。

数据中心能耗主要由IT 设备、空调系统、供配电系统和照明系统组成［8］,其中前两者占比最高,通常占到数据中心总能耗的85%,而后两者的功耗则相对稳定,占比很小,进行能耗优化时可以忽略不计［9］。当前,数据中心能效利用率较低、节能潜力大,有必要从IT 设备和空调设备的能耗特性着手,分析两者在能耗上的相关性,建立数据中心能效优化方法［10］。

现有文献通常采用基于系统利用率的线性模型来表示IT 设备能耗［11］。文献［12］细化了IT 设备内部各元件的能耗特性。文献［13］通过引入能效比指标对空调设备能耗进行优化建模。文献［14］通过热流仿真对空调能耗进行优化,提供了最佳空调布置方式。文献［15］建立数据中心热循环模型,以IT 设备和空调设备总功耗最小为目标,对IT 设备的算力分配和空调设备的送风温度进行多目标优化。文献［16］考虑了IT 设备休眠对能效优化的影响,以IT设备和空调设备总功耗最小为目标,通过迭代运算得到IT 设备的休眠状态和负载分配,实现总功耗的最小化。

上述研究通过设备内部自身的节能设计或建立单时段能效优化模型,实现了IT 设备算力和空调设备送风温度的分配优化,降低了数据中心总能耗。然而,现有模型仅考虑单时段能效优化模型,忽略了IT 设备和空调设备的时段间耦合关系,实质上是将模型视为多个单时段优化模型独立进行求解。在实施过程中,其优化策略可能出现设备损耗过大或算力供需不平衡等问题。因此,有必要考虑其能效的时段耦合性,通过数据中心的多时段高效运营管理动态调整IT 设备的运行状态,关闭或休眠效率低的IT 设备,以提升整体能效、实现数据中心的绿色可持续发展。

本文综合考虑了数据中心IT 设备和空调设备的能耗特性与换热耦合关系,以及IT 设备的时段间启停待机和爬坡约束关系,建立了基于设备耦合的数据中心多时段能效优化模型。针对时段耦合约束以及IT 设备数量大导致的大量整数变量带来的计算效率难题,分别提出前瞻解耦算法和IT 设备聚合算法进行求解。最后,通过算例分析验证了本文方法的可行性和有效性。

1 数据中心主要设备的运行特性

如前文所述,数据中心的主要能耗设备为IT 设备与空调设备。空调设备能耗建模通常采用“功率及面积法”［17］。目前,IT 设备应用最广的能耗建模方式主要有加性模型和线性模型两种模型。

加性模型是指将整个服务器的能耗形式转化成服务器子结构的能耗之和［18-21］。缺点是现有的平台只可以测量出服务器总能耗,对子系统的能耗值尚不能独立地测量出来。另一类最常用的服务器能耗模型是基于系统利用率的线性模型［22］,其核心思想是将IT 设备能耗分为处理计算负载时产生的功耗（计算功耗）和电子元器件漏电产生的功耗损失（漏电功耗）两部分。该模型自提出后,一直被用来对数据中心能耗进行建模,可以更加精确地追踪IT 设备的功率使用情况［23］。因此,本文采取线性模型对IT设备进行能耗建模。

1.1 IT 设备的运行特性与建模

1）IT 设备的计算功耗

现有研究表明［24］,动态功耗与IT 设备的资源利用率近似呈一阶线性关系。计算功耗Pcal可以表示为:

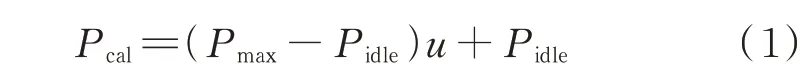
式中:Pidle为静态功率；Pmax为满载功率；u∈［0,1］,为IT 设备的资源利用率；(Pmax-Pidle)u为动态功耗。

2）IT 设备的漏电功耗

现有研究通过一阶线性函数f（∙）对其进行简化［25］:

特别地,IT 设备除开启、关闭两个状态外,还有待机状态。当IT 设备处于待机休眠状态时,会自动降低电压与频率从而达到节能效果,此时的功耗为一个较小的恒定值Psleep,通常为20 W 左右［10］。令Ii(t)为IT 设备i在t时段的状态变量,Ii(t)取2、1、0,分别代表开启、待机和关闭3 种状态,则t时段IT设备i的能耗可以表示为:

1.2 空调设备的运行特性与建模

1）空调设备的冷负荷

在数据中心工作过程的主要冷负荷来自IT 设备产生的热量和环境热量,其中前者约占整个数据中心空调冷负荷的90%,近似计算可只考虑前者［10］。表示如下:

式中:Qaircon为空调设备冷负荷总量；Q1为IT 设备产生的热量（大多数IT 设备的生产厂商均能提供IT设备的耗电量和散热量,其散热量约为耗电量的97%［17］）；Q2为环境热量。分别表示如下［17］:

1.3 IT 与空调设备的换热模型

IT 设备在工作时会产生大量的热量,且其稳定运行又需要将环境温度控制在安全阈值以内。因此,需要空调设备吸收IT 设备和环境产生的热量,使得IT 设备运行在正常的温度范围区间内,保证其正常运行。在IT 设备工作过程中,可以认为其耗电量的97%转化为热量,并被流经的冷空气带走,这种现象在热力学中称为对流换热现象,它是IT 设备能耗和空调设备能耗模型的核心关系。对流换热现象可以用等效热阻模型来描述,其表达式如下:

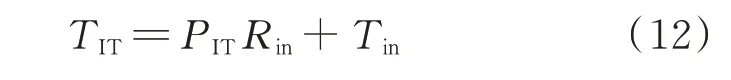
式中:Tin为入口气流温度；Rin为入口对流换热等效热阻,与换热面积、换热面气流相对速度以及气体和固体的物理性质有关,而在冷却气流与IT 设备的对流换热过程中,Rin仅是换热面气体相对速度的函数。本文研究中将流经服务器的气流设定为恒定值,此时Rin可以认为是一个常量,取Rin=0.014 7 K/W［25］。

IT 设备的入口气流温度与空调设备的送风温度的关系可以表示为［25］:

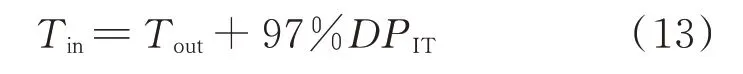
式中:D为传热系数,仅与设备的布置情况有关,本文研究中将设备视为均匀布置,故D可近似为常数。

该模型的本质是能量守恒定律,其物理含义是在IT 设备达到热平衡状态时,其发出的热量与入口冷空气热量之和等于出口热空气的热量。

综上所述,数据中心总能耗Ptotal可近似视为IT设备的运行能耗、IT 设备的待机能耗和空调设备的运行能耗之和,即

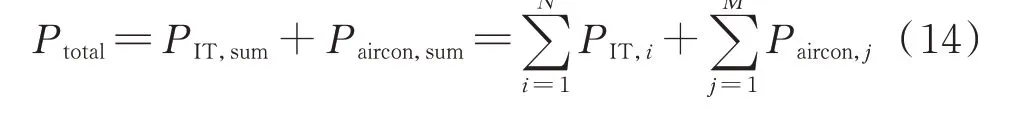
式中:M为空调设备总数；PIT,sum为IT 设备总能耗；Paircon,sum为空调设备总能耗；PIT,i和Paircon,j分别为第i台IT 设备和第j台空调设备的能耗。

2 基于多时段设备耦合的数据中心能效优化模型

数据中心能耗优化问题的本质是在数据中心总算力满足当前算力需求,以及空调制冷量保证IT 设备正常运行的前提下,数据中心的能效达到最优。

本文优化模型以数据中心运行成本和IT 设备启停成本之和为目标函数；决策变量包括空调设备送风温度Tout和每台IT 设备的资源利用率u及其运行状态（开启、关闭和待机）；约束条件包括算力需求约束、空调送风温度范围约束、芯片温度上限约束、入口气流温度范围约束、IT 设备爬坡约束以及IT设备停机时间约束。

2.1 目标函数

本文模型的IT 设备共考虑了开启、关闭和待机3 个状态。相较于直接关闭,待机状态避免了启停对设备造成的损耗,能显著减少启停成本。因此,若待机功耗成本小于启停成本则优先选择待机,从而降低总成本,反之则优先选择启停。

考虑IT 设备启停或待机对实现数据中心动态能效最优非常重要。根据美国劳伦斯伯克利国家实验室给出的IT 设备性能与耗电量的关系［27］,资源利用率极低（10%～20%）的IT 设备能耗也能达到满载能耗的60%左右。

目前,数据中心IT 设备主要存在的问题有以下两个方面［10］:一是多数IT 设备的资源利用率都特别低,只有10%～20%,而这些IT 设备运行时需要消耗较多的能耗,同时给IT 设备的管理也带来了诸多不便；二是不少数据中心有很多老旧、闲置的IT 设备,这些设备由于各种原因基本上不再被使用,但由于缺乏合理的管理仍在开机运转,也消耗了许多能耗。因此,有必要根据算力需求压力,动态调整IT设备的运行状态,关闭或者休眠效率低的IT 设备,这样既能提升整体的资源利用率,将IT 设备的用电损耗降到最低,同时又不影响用户的算力需求。考虑到数据中心的空调设备通常为一个集中控制的中央空调系统,需要全年不间断且稳定、可靠地制冷,其送风温度调节范围窄且波动较小,因此,现有研究一般不考虑空调设备的启停与爬坡约束［10］。

2.2 约束条件

1）算力需求约束:

式中:PIT,i(t)|Ii(t)=1表示第i台IT 设备处于启动状态时在t时段的功率；RIT为爬坡系数；T为总时段数。式（20）限制了IT 设备的爬坡速率。

2.3 模型求解

本文模型不仅要确定IT 设备的算力分配,而且要确定多个时段的IT 设备的运行状态。其数学本质为混合整数规划（mixed integer programming,MIP）问题。分支定界法［28］在解决这类问题时具有可以求得最优解、平均速度快的优点,因此,本文采用分支定界法对优化模型进行求解。

分支定界法的基本思想是对有约束条件的最优化问题的所有可行解（数量有限）空间进行搜索。分支定界法在具体执行时,是把全部可行解的空间不断分割为越来越小的子集（也称为分支）,并为每个子集内解的值计算一个下界或上界。在每次分支后,对界限超出已知可行解值的那些子集就不再进一步分支。这样,解的许多子集就可以不予考虑,从而缩小了搜索范围。这一过程一直进行到找出可行解为止［28］。具体的求解过程本文不再赘述。

3 基于多时段设备耦合的数据中心能效优化求解算法

3.1 计算难点分析

对于上文模型,若直接对该模型进行求解,则计算效率难以满足在线计算要求,原因是存在以下问题:

1）时段耦合问题。多时段数据中心能效优化问题具有时段耦合性,在模型计算中将引入整数变量和大量时段耦合约束,相对于单时段约束求解更加困难。

2）IT 设备组合问题。多时段数据中心能效优化问题的数学本质是混合整数规划问题。随着需要确定状态的IT 设备数量和调度时段数增多,整数变量的增多会造成“组合爆炸”问题,求解计算规模越来越大,计算时间也越来越长。

因此,本文针对不同的求解难点,对应提出适用于在线计算的多时段数据中心能效优化算法,以提高求解效率。

3.2 前瞻解耦算法

针对问题1）,本文提出前瞻解耦算法。基本思想是通过判断时段耦合约束是否起作用,从而减少数据中心能效优化问题的求解时间。

设Ni为IT 设备i的功率从下限到上限全程上升所需的最少时段数,表示如下:

式中:PIT,i,max和PIT,i,min分别为第i台IT 设备的能耗最大值与最小值。

设m为任意整数。在时段t的前m个时段内,将IT 设备分为如下两个集合:快速上升集合Nf和慢速上升集合Ns。其分类依据是IT 设备能否从最小功率上升至最大功率,能则分入快速上升集合,否则分入慢速上升集合。即快速上升集合的IT 设备从其最小功率上升至最大功率的最短时间小于m个时段,而慢速上升集合的IT 设备则大于m个时段。分别表示如下:

对于任意m,式（25）成立至少一次,则说明总算力需求在该m个时段的上升值超过了um,max。此时不能解耦。

对于任意m,式（25）均取小于或等于号,则um,max大于或等于总算力需求的变化值。此时对于时段t,时段耦合约束不起作用,这就是解耦条件。

由于时段耦合约束起作用的次数减少,该解耦算法可以显著减少数据中心能效优化问题的求解时间。

3.3 IT 设备聚合算法

整数变量主要由IT 设备数N和调度时段数的乘积组成（NT）。IT 设备共有开启、关闭和待机3 种状态。理论上,可基于枚举法穷举所有可能的IT 设备状态组合,得到最优的组合结果。但当有N台IT设备和T个调度时段时,一共有(3N-1)T种组合方式。

针对问题2）,本文提出IT 设备聚合算法。基本思想是利用一台等效IT 设备来表征聚合簇中所有IT 设备的特性,并替代聚合簇中的所有IT 设备参与优化模型的计算。

数据中心的IT 设备通常为大量采购,型号和规格参数种类单一。假设数据中心共有x种类型的IT 设备,第i类的设备台数为ni。对于一类具有相同规格参数的IT 设备,其等效设备的参数表示如下:

3.4 计算流程

本文提出的多时段数据中心能效优化求解方法大致包括4 个步骤,具体流程如图1 所示。

图1 多时段数据中心能效优化方法流程图Fig.1 Flow chart of multi-period optimization method for energy efficiency of data center

步骤1:首先采用式（26）—式（28）的IT 设备聚合算法对所有的IT 设备进行等效简化,减少模型计算的整数变量,计算得到简化后的等效参数ueq,i、PIT,eq,i和RIT,eq,i。

步骤2:将等效参数代入式（1）—式（5）,建立等效IT 设备的能耗模型。将空调设备参数代入式（6）—式（11）,建立空调设备能耗模型。将气流参数代入式（12）、式（13）,建立换热模型。

步骤3:基于步骤2 的模型建立数据中心的多时段能效优化模型。利用式（21）—式（25）的前瞻解耦算法分解时段间耦合约束,减少其起作用的次数,加快求解速率。

步骤4:利用分支定界法［28］求解简化后的模型,得到IT 设备的算力分配和空调设备送风温度的最终优化结果。

4 算例仿真

为验证本文方法的实用性和高效性,使用MATLAB 软件,选取国内某互联网企业的大型数据中心的实际运行数据进行能效优化仿真。该数据中心配备有10 万台均匀排布的IT 设备及一个中央空调系统。算例的优化步长为5 s［29］,优化总时间为24 h。算例中的IT 设备和空调设备的运行特性和参数见附录A 表A1。

分别选取波动较小的算力需求曲线数据和波动较大的算力需求曲线数据两个算例（算例a 和算例b）,对数据中心在不同使用情形下的运行方式进行优化,分析优化结果。算力需求曲线数据见附录A图A1。

本文所提多时段数据中心能效优化方法大致包含4 个步骤:设备等效简化、建立优化模型、前瞻解耦加速和输出优化结果。首先,采用IT 设备聚合算法对所有IT 设备进行等效简化；其次,计算等效IT设备的等效参数并建立其能耗模型；然后,利用前瞻解耦算法分解时段间耦合约束；最后,利用分支定界法求解得到最终优化结果。

采用M1、M2、M3 方法与不进行能效优化（M4）方法进行对比:

M1:本文所提多时段数据中心能效优化方法；

M2:直接求解的M1 方法,不采用本文第3 章的设备聚合及前瞻解耦加速算法；

M3:传统的单时段数据中心能效优化方法［16］；

M4:不进行能效优化,即所有IT 设备均保持开机,不对其运行状态与算力分配进行运营管理,空调设备设为恒定25 ℃的运行方式,用于对照M1、M2、M3 方法的优化效果。

分析优化结果,比较前3 种优化方法相较于M4方法的优化效果和计算效率。本文采用总成本作为衡量优化效果的指标。如2.1 节所述,数据中心的总成本大致包含运行成本和启停成本两部分。运行成本是指数据中心各设备正常运行的成本,包含电费、正常使用造成的损耗等；启停成本是指IT 设备启停时的通电和断电过程对IT 设备的硬件造成的损耗。数据中心的总成本C计算公式如下:

4.1 算例a 分析

当算力需求曲线波动较小时,如附录A 图A1所示,代入算例a 数据,得到M1、M2、M3 方法的优化结果如表1 所示。优化后的IT 设备运行状态、算力u分配和空调的送风温度见附录B 图B1—图B3。

表1 算例a 结果比较Table 1 Result comparison of case a

1）总成本比较:M4 方法最高,为179.54 万元；M1 和M2 方 法 最 低,均 为115.64 万 元；M3 方 法 较M4 方法虽有所减少,但减少不多。这是因为M1 与M2 方法考虑了时段间耦合约束,一定程度上限制了IT 设备的频繁启停。而M3 方法的IT 设备启停更为频繁,能耗和运行损耗更多,故其总成本较高。

2）PUE 值比较:相较于M4 方法,M1、M2、M3方法的PUE 值均大幅减少,分别为1.274 9、1.274 9和1.455 2,且M3 方法略大于M1 和M2 方法。这是因为M1、M2、M3 方法通过优化IT 设备的运行状态与算力分配,关闭了闲置的IT 设备,提高了IT 设备的利用效率,降低了PUE 值。同时,由于M1 和M2方法考虑了时段间耦合约束,通过数据中心的多时段高效运营管理提高了IT 设备的能源利用率,降低了PUE 值。

3）计算时间比较:M2 方法的计算时间最长,为10 845.01 s；M1 和M3 方法的计算时间较短,分别为61.91 s 和184.56 s,其中M1 方法的速度最快。这是因为M2 方法未采用加速算法,大量整数变量和时段间耦合约束导致计算速度慢；而M3 方法未考虑时段间耦合约束,计算速度较快；M1 方法采用前瞻解耦算法和IT 设备聚合算法,减少了时段间耦合约束起作用次数和整数变量,极大地提高了计算速度,所需时间最短。

4.2 算例b 分析

当算力需求曲线波动较大时,如附录A 图A1所示,代入算例b 数据,得到M1、M2、M3 方法的优化结果如表2 所示。优化后的IT 设备启停状况、算力u分配和空调设备的送风温度见附录B 图B4—图B6。

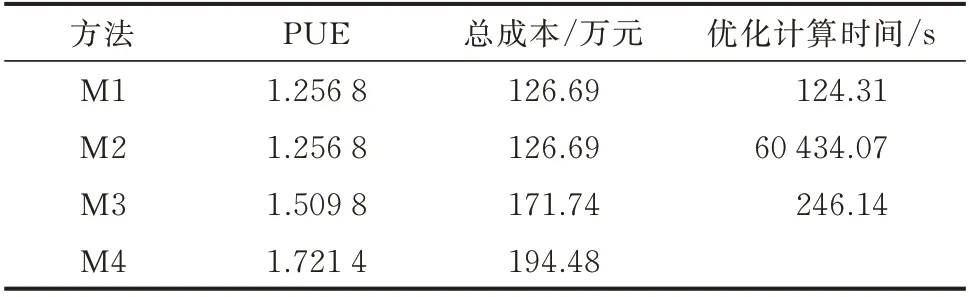
表2 算例b 结果比较Table 2 Result comparison of case b

1）总成本比较:M4 方法的总成本最高,为194.48 万 元；M1 和M2 方 法 的 总 成 本 最 低,均 为126.69 万元；M3 方法的总成本为171.74 万元,这是因为其启停频率和总能耗相对M1 和M2 方法较高,故其总成本较高。M1 和M2 方法考虑了时段间的能效耦合性,通过多时段优化分析,对IT 设备的运行状态进行高效管理,降低了总成本。

2）PUE 值 比 较:相 比 于 优 化 前 的PUE 值1.721 4,M1、M2 方法通过优化IT 设备的运行状态与算力分配,关闭或休眠了闲置的IT 设备,提高了IT 设备的利用效率,极大地降低了PUE 值,仅为1.256 8；而M3 方法的PUE 值为1.509 8,优化效果较M1 和M2 方法不是很明显。

3）计算时间比较:M2 方法的计算时间最长,为60 434.07 s；M3 方 法 的 计 算 时 间 为246.14 s；M1 方法的计算速度最快,为124.31 s。这是因为M2 方法未采用第3 章的时段解耦和设备聚合加速算法,含有大量整数变量,较大的算力需求曲线波动也使得时段间耦合约束更加复杂,导致计算速度最慢；M1方法采用前瞻解耦算法和IT 设备聚合算法,减少了时段间耦合约束起作用次数和求解过程中整数变量的个数,极大地提高了计算速度,所需时间最短。

4.3 IT 设备爬坡约束的必要性

为了验证IT 设备爬坡约束（式（20））的必要性,最直接的方法就是去掉M1 方法中的式（20）,并比较其优化结果与原M1 方法的结果是否一致。若基本一致则式（20）几乎不起作用,无须考虑；反之则需要考虑式（20）。不妨令去掉IT 设备爬坡约束的M1 方法为M5 方法,得到M5 方法的优化结果并与M1 方法进行比较,如表3 所示。

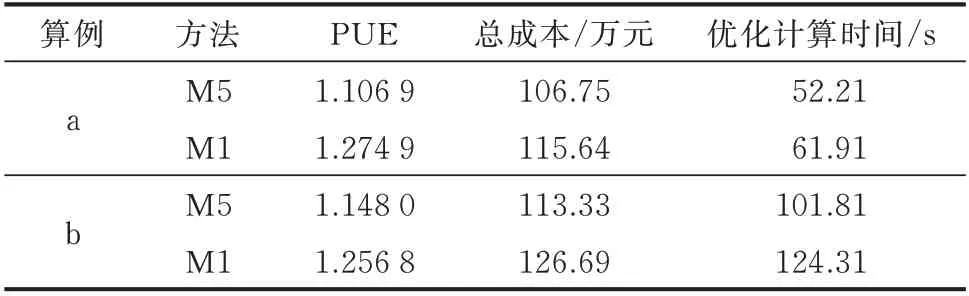
表3 M5 方法与M1 方法的结果比较Table 3 Result comparison of M5 method and M1 method

由上述结果可知,由于失去了爬坡约束（式（20））的约束条件,无论是算例a 还是b,M5 方法的各项指标均取得了远小于M1 方法的结果。此时,由于失去了式（20）的约束条件,M5 方法的优化结果会出现IT 设备功率变化速率过大,超出IT 设备爬坡约束上限26 W/s 的情况。例如:算例a 在12:15:05 时刻前一时段的IT 设备爬坡速率达到41.21 W/s；算例b 在21:03:35 时刻前一时段的IT设备爬坡速率达到109.36 W/s。而本文M1 方法则不会出现IT 设备功率变化速率过大,超出IT 设备爬坡约束上限的问题。因此,有必要考虑设备爬坡约束。

综上所述,M3 方法在算力需求曲线波动较大和较小两种情况下求得的PUE 值、总成本和优化计算时间均高于M1 和M2 方法,优化效果较后两者不明显。而本文提出的M1 方法在两种情况下均取得了较好的结果,在大幅降低PUE 值的同时,一定程度上限制了IT 设备的启停频率,使得总成本最低,并且采用加速算法大幅提高了计算速度。因此,本文提出的多时段数据中心能效优化方法较传统方法更合理,更符合工程实际。

5 结语

目前,数据中心能耗问题日益突出,但现有研究忽略了数据中心能效的时段耦合性,其优化策略往往不符合实际。针对数据中心高能耗所带来的新挑战,本文在IT 设备和空调设备各自能耗模型的基础上,综合考虑数据中心IT 设备和空调设备的设备间耦合关系以及时段间耦合关系,建立了基于多时段设备耦合的数据中心能效优化模型。针对时段耦合和IT 设备组合带来的求解难题,分别提出前瞻解耦算法和IT 设备聚合算法。算例分析结果表明,所提方法可快速、有效地提高数据中心的能效。本文方法为数据中心的节能降耗运行、IT 设备的启停待机与算力、空调设备的送风温度等参数设置提供了合理参考,为数据中心能效管理系统级建模及运行优化提供了理论支撑。

随着电力系统中数据中心负荷比例的提高,数据中心能耗特性对电力系统的稳定性影响将逐步变大。数据中心的节能降耗有助于调节电力系统供需平衡,缓解系统线路阻塞,保障电力系统安全可靠运行。这将是下一步的研究方向。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。