考虑交互轨迹预测的自动驾驶运动规划算法

刘启冉， 连 静，2， 陈 实， 范 蓉

(1.大连理工大学 汽车工程学院， 辽宁 大连 116024； 2.大连理工大学 工业装备结构分析国家重点实验室， 辽宁 大连 116024)

随着人工智能的发展，自动驾驶技术在提升交通安全和效率等方面发挥重要作用.在结构化道路场景中，考虑周围车辆之间的交互轨迹预测是自动驾驶汽车运动规划的一大挑战[1-2].Song等[3]提出使用人工势场法预测周围车辆运动的轨迹监管器，并进行碰撞风险检查，根据速度分布进行轨迹规划，该方法考虑道路的几何形状提高舒适性，但实时性差.Yang等[4]利用无迹卡尔曼滤波实时预测周围车辆轨迹的不确定性，并传入到模型预测控制器中实现避障规划，但该方法没有考虑周围车辆之间的交互.Lin等[5]提出一种具有驾驶员行驶风格、信息交互、动态交通参与者轨迹预测功能的局部轨迹规划器，仿真结果表明，当存在碰撞风险时该规划器可以重新规划运动轨迹.Lee等[6]提出计算周围车辆潜在风险的预测占用图(predictive occupancy map， POM)，然后通过POM规划出风险最低的安全轨迹.但上述方法只能应用在车辆间交互较少的简单场景中.

为提升自动驾驶汽车运动规划在复杂场景中的应用性能，基于学习的轨迹预测方法快速发展.Jeong等[7]利用长短时记忆-递归神经网络对周围车辆的运动进行预测，但该方法适用范围有限.Li等[8]设计一种分层逆强化学习的轨迹预测框架，同时考虑周围交通参与者之间的交互动作，但计算复杂.Messaoud等[9]提出一个基于注意机制的车辆多模态轨迹预测模型.但当前基于数据驱动的轨迹预测模型存在可解释性差、复杂度高等问题.

针对上述方法存在的问题，许多研究者对Helbing等[10]提出的社会力模型(social force model，SFM)进行改进，将其应用到轨迹预测上.杨文彦等[11]利用社会力模型对人车混合路口中的行人轨迹进行预测，但没有预测周围车辆之间的交互轨迹.Yoon等[12]基于驾驶员行为的社会特性，构建改进社会力模型进行车辆轨迹预测，但该方法对模型参数过于敏感.

基于以上分析，本文提出一种基于交互轨迹预测的自动驾驶运动规划算法.首先构建改进社会力模型，实现多车交互场景下的车辆轨迹预测，并基于Frenet坐标系采样得到横向轨迹序列和纵向轨迹序列，通过时间离散化和坐标系转换合成运动规划的轨迹集合.然后进行轨迹检查，利用时空占用图生成轨迹集合与预测轨迹投影点之间的最短距离进行碰撞检查，为提高算法的实时性，检查轨迹的加速度和曲率.最后设计代价函数，评估候选轨迹集合中的最优运动轨迹.仿真结果表明，基于本文方法进行的运动规划，在提高规划轨迹安全性的同时提高规划的舒适性和行驶效率.

1 交互轨迹预测

1.1 改进社会力模型

图1 社会力分析示意图

(1)

1.2 目标驱动力

目标驱动力Fd为驱动车辆以最优的速度尽快向目的地运动的主要动力，当受到周围交通参与者和环境的干扰时，目标驱动力作用于车辆向期望速度运动.目标驱动力的表达式为

(2)

式中：ve为期望速度，方向为观测时间步长内车辆起点指向终点的方向；vc为实际速度，由式(1)计算得到；τd为反应时间，表示车辆速度变化的快慢.

1.3 车辆间相互作用力

为避免发生碰撞，车辆行驶时会与当前所在车道和相邻车道上一定范围内车辆保持一定的距离.距离越近，作用在主车上的排斥力越大.车辆ci受到周围车辆的作用力为

(3)

式中：Av为车辆间相互作用力的强度；rv为考虑车辆几何形状特性的车辆间距离；Bv为车辆间相互作用力的范围；nij为车辆cj指向车辆ci中心的单位向量.

1.4 边界约束力

在交通法规和道路环境的约束下，行驶在道路上的车辆会受到车道线及道路边界的作用，使主车保持在当前所在车道的中心线位置.边界约束力的表达式为

(4)

式中：Ab为边界约束力的作用强度；db为车辆与边界的距离；Bb为边界约束力的作用范围；nb为垂直边界指向车辆中心的单位向量.

2 运动规划算法

2.1 Frenet坐标系

由于车辆动力学和输入到控制模块的轨迹是基于笛卡尔坐标系定义的，因此规划后得到的轨迹需进行坐标系转换，如图2所示.在全局笛卡尔坐标系下，车辆的运动状态可以描述为[x，θt，kt，vt，at]，其中：x为车辆位置，x=(xt，yt)；θt为方位角；kt为曲率；vt为速度；at为加速度.τr，nr分别为参考线上某一点的单位切向量和单位法向量；τt，nt分别为实际行驶轨迹上某一点的单位切向量和单位法向量；r(s)为笛卡尔坐标系下车辆当前位置在参考线上的投影点的位置，r(s)=(xr，yr).

图2 Frenet坐标系与全局笛卡尔坐标系的转换示意图

(5)

基于文献[16]的公式推导，Frenet坐标系与全局笛卡尔坐标系的转换可由式(6)确定.

(6)

2.2 轨迹集合求解

关于时间t的三维运动规划问题在Frenet坐标系下可以分解为横向运动规划d(t)和纵向运动规划s(t).本文选用式(7)所示的五次多项式来规划运动轨迹p(t).

p(t)=α0+α1t+α2t2+α3t3+α4t4+α5t5

.

(7)

(8)

(9)

令t0=0简化计算，可得

(10)

设t1=T，则系数α3，α4，α5可由式(11)求解：

(11)

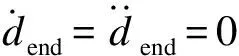
2.3 轨迹检查

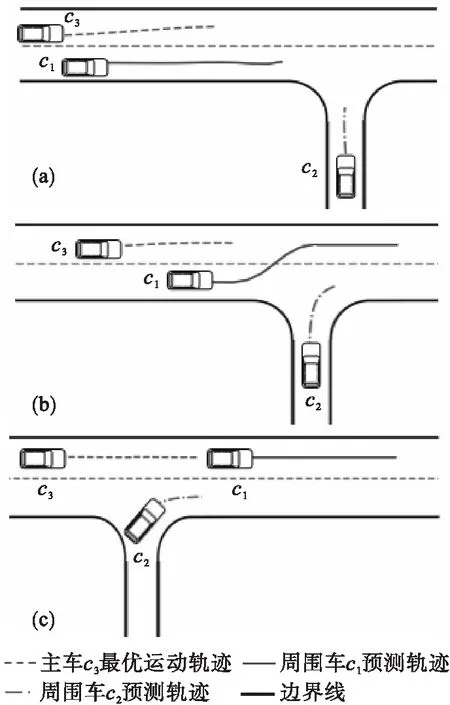
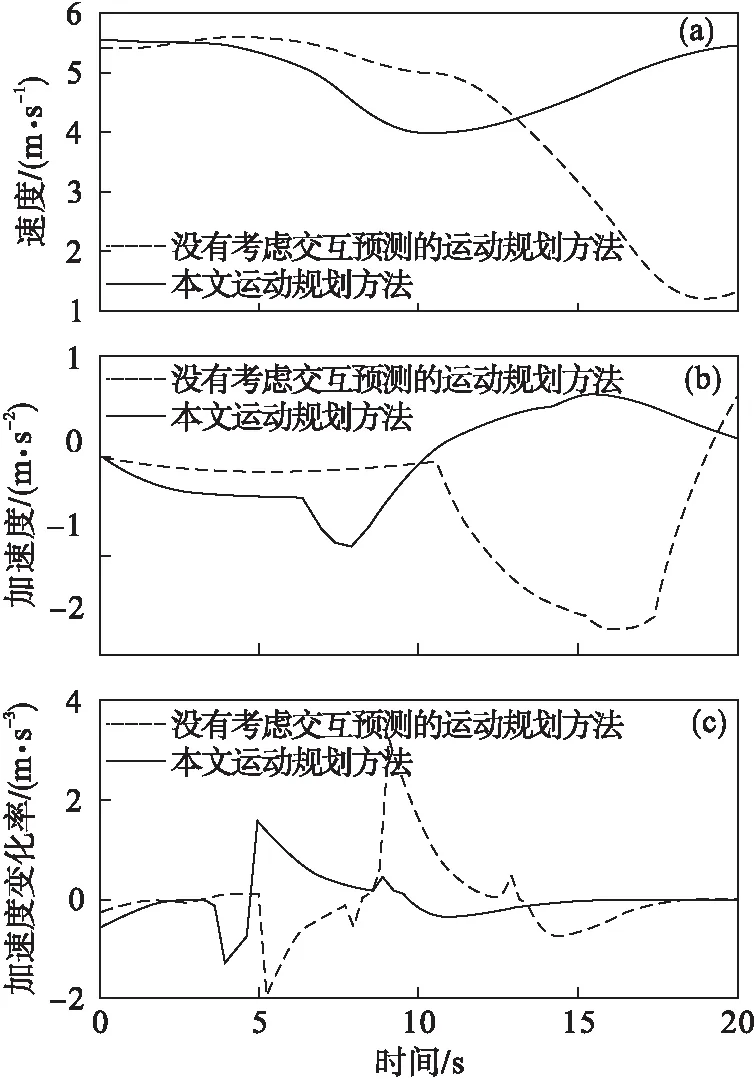
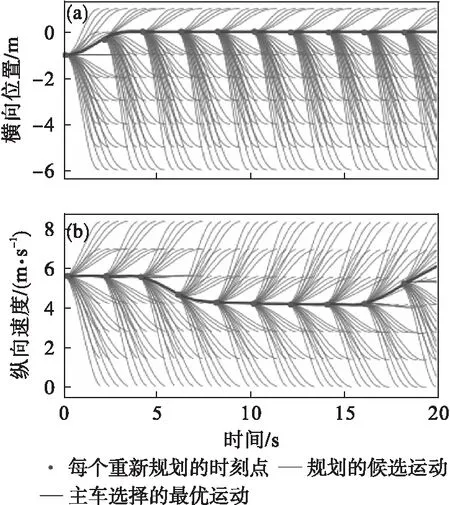
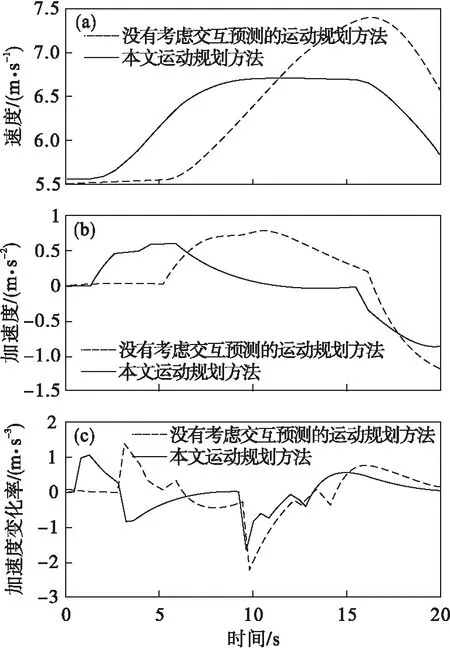
为进行碰撞检查，基于文献[17]提出的时空占用图如图3所示，记碰撞点为P(x，y，t).本文将上述得到的周围车辆预测轨迹和主车的轨迹集合投影到时空占用图中，并分别计算轨迹集合中每条轨迹的投影点与预测轨迹投影点之间的距离，当计算得到轨迹的最短距离dmin小于安全阈值时，即0

图3 时空占用图

由于车辆本身运动学、动力学及行驶工况的限制，同时为提高算法的实时性，去除没有通过最大加速度和最大曲率约束条件的轨迹，得到候选轨迹集合.通过加速度检查和曲率检查[18]的条件为

(12)

式中：api为轨迹i离散化后相应轨迹点的加速度；kpi为轨迹i离散化后相应轨迹点的曲率；N为轨迹离散化后轨迹点的最大数量；amax和kmax分别为最大加速度和最大曲率.

2.4 代价函数设计

设计评估候选轨迹集合的代价函数[19]，求解候选轨迹中代价函数值最小的即为最优运动轨迹.

Ctotal=wtCt+wpCp+wsCs+wjCj.

(13)

(14)

式中：Cs表示从安全性考虑对碰撞的代价；l=(xi-xob)2+(yi-yob)2为障碍物到轨迹的距离，(xob，yob)为障碍物的位置；由于车辆几何尺寸的影响，设ln为安全距离阈值，lc为碰撞距离阈值，当lc≤l≤ln时，距离障碍物越近则发生碰撞的可能性越大；ρ为障碍物危险程度距离影响因子，其与车辆的车速v成正比.

(15)

3 仿真与结果分析

车辆行驶行为主要分为纵向行为和横向行为，所以本文分别设计减速行驶场景和换道行驶场景来验证所提算法的有效性.利用Matlab中的遗传算法(genetic algorithm,GA)函数[20]对改进社会力模型的参数Av，Bv，Ab，Bb进行标定，具体标定结果如表1所示.针对关键采样参数，经过大量的仿真实验总结，本文具体取值如表2所示.

表1 模型参数标定结果

表2 仿真参数

3.1 减速行驶场景

图4所示的减速行驶场景中，主车c3初始车速为5.5 m/s，周围车c1速度为8 m/s，周围车c2速度为2 m/s，从c1与c2的交互预测轨迹可以看出，c2从岔口驶出右转时距离较高车速的c1较近，所以c1在行驶过程中为避免与c2发生碰撞突然向左驶入主车c3当前所在车道.

图4 减速场景

若主车在运动规划中不考虑周围车辆之间的交互预测轨迹，根据图5所示的减速行驶场景下时空占用图，主车c3在7.5 s时与c1存在碰撞风险.

图5 减速场景下时空占用图

如图6a所示，没有考虑多车交互的运动规划对c1换道动作反应不及时，主车在0～10 s的时间内仍处于较高行驶速度，在10 s时才对已经驶入主车c3当前所在车道的c1做出相应减速，导致速度曲线不平稳，降低行驶效率同时增加碰撞风险.在图6b，6c中，加速度和加速度变化率波动较大，降低乘车舒适性.相对于没有考虑轨迹预测的运动规划，本文方法规划出的速度跟随曲线更加平稳，加速度、加速度变化率波动更小，说明驾驶舒适性更高.因此，本文方法可以规划出一条最优运动轨迹.

图6 减速场景下结果对比

在图7中，基于本文运动规划方法主车c3提前预测到周围车辆的运动轨迹，在纵向运动轨迹候选集合中，为避免与c1产生碰撞，c3的最优纵向运动在4 s时提前减速.同时c3从初始位置向车道中心线规划并沿车道中心线向前行驶，为保证行驶效率，在减速确保安全后进行加速.

图7 减速场景下运动轨迹候选集合

3.2 换道行驶场景

图8所示换道行驶场景中，主车c3初始车速为5.5 m/s，周围车c1速度为4 m/s，周围车c2速度为8 m/s.根据预测c1与c2的运动轨迹，c2突然驶入c1当前所在车道，c1减速行驶，因而c3提前向左换道.

图8 换道场景

从图9所示的时空占用图中可以看出，若主车c3不对周围车辆之间交互的预测轨迹进行考虑，则不会提前采取换道决策，在11 s时存在与c1发生碰撞的风险.

图9 换道场景下时空占用图

如图10所示，没有考虑预测轨迹间交互的运动规划方法所规划的速度曲线滞后2 s进行换道，降低行车效率，同时速度变化较大，降低行驶舒适性.本文方法提前决策驾驶行为，规划出更加平稳的速度变化曲线，加速度和加速度变化率波动程度也较小，提升了行驶舒适性和行驶效率.

图10 换道场景下结果对比

基于本文所提方法提前对周围车辆的交互运动轨迹进行预测，在图11中，主车c3考虑c2突然换道和c1减速的预测轨迹，为避免与c1发生碰撞，c3在4 s时向左加速换道，保证行驶安全性.综上，本文提出的运动规划算法适用多种交互场景，可以规划出安全性、舒适性和行驶效率更高的运动轨迹，为自动驾驶汽车降低碰撞风险提供依据.

图11 换道场景下运动轨迹候选集合

4 结 语

本文针对自动驾驶汽车运动规划存在的交互问题，构建改进社会力模型，提出考虑周围车辆间交互轨迹预测的运动规划算法.首先利用改进社会力模型对周围车辆的行驶轨迹进行预测.然后基于Frenet坐标系采样得到自动驾驶汽车的轨迹集合，将轨迹集合与预测轨迹投影到时空占用图上，计算投影点之间的最短距离，并结合加速度和曲率检查对轨迹进行筛选，得到候选轨迹集合.最后求解候选轨迹集合中代价函数最小的轨迹即为最优运动轨迹.仿真结果表明，本文提出的算法有效地提高了运动轨迹的安全性、舒适性和行驶效率.在未来的研究工作中，考虑感知盲区的不确定性对轨迹预测的概率影响和提高运动规划算法对复杂工况的自适应性是今后的重要研究方向.