Modal Logic of Multivalued Frames over Inversely Well-Ordered Sets*

Fan He

Abstract.Multivalued frames generalize Kripke frames via introducing a set of values for pairs of states.A set of values Q is supposed to be an inversely well-ordered set.The intended multimodal language is interpreted in models based on multivalued frames over Q.Goldblatt-Thomason theorems for certain classes of Q-frames are established.Normal Q-modal logics are introduced,and some completeness results are naturally given by adjusting the canonical model method.Makinson’s classification theorem as well as some logical properties are established for normal Q-modal logics.

1 Introduction

Multimodal logic is a name for a bunch of modal logics which formalize reasoning about multiple modalities.The following passage from Dana Scott is often quoted when the significance of multimodal logic is concerned:

Here is what I consider one of the biggest mistakes of all in modal logic:concentration on a system with just one modal operator.The only way to have any philosophically significant results in deontic logic or epistemic logic is to combine those operators with:tense operators(otherwise how can you formulate principles of change?);the logical operators (otherwise how can you compare the relative with the absolute?);the operators like historical or physical necessity (otherwise how can you relate the agent to his environment?);and so on and so on.([11],p.161)Scott emphasizes many faces of a philosophical modality.For instance,the notion of belief should be combined with tense if the change or update of an agent’s belief is concerned.Although the combination is needed for some philosophical purposes,the exact way of combination which represents the intrinsic corelation between modalities has not been well-explored yet.

A direct response to Scott’s remark is the development of multimodal logic in the study of reasoning in multiagent systems.Multimodal logics have been widely studied in the literature (e.g.,[2,3]).For example,the multiagent epistemic logic requires a knowledge operatorKafor each agenta(e.g.,[13]).A typical example is the multimodal logic S5 as the standard multiagent epistemic logic.In an idealistic multiagent model,agents are usually assumed to be independent,i.e.,every agent makes reasoning in situations without disturbance from other agents.However,if agents are organized or structured in a certain way,the corresponding modalities in logic must be connected in the same way.A sort of combination is shown in propositional dynamic logic where each programπis assigned with a modality[π],and the composition,choice and repetition of programs are presented by interaction axioms between modalities(e.g.,[9]).

From the semantic perspective,relational semantics for modal logic has been well-explored.A Kripke frame (‘K-frame’ for short) for a monomodal language is a pair (W,R) whereWis a non-empty set of states,andRis a binary relation onW.Each modal formula □φis true at a statewif and only ifφis true at allRaccessible states ofw(e.g.,[1,2]).An accessibility relationRis indeed abivalentfunctionR：W ×W→{0,1}.In the present work,we generalize Kripke frames by changing the set{0,1}into a set of valuesQand obtainmultivaluedframes.This leads to a general framework for the investigation of multimodal logics.One can impose additional structure onQ,and study the modal logics of these special class of frames.

One should mention that two sorts of semantics for many-valued modal logic are given by Fitting[6,7].LetTbe a finite distributive lattice the elements of which are accounted as values.Every formulaφwill take a valueV(w,φ)at the statewin a model.In Fitting’s second version,a model is a triple (W,R,V) whereW∅andRis a multivalued relation onW,i.e.,a functionR：W ×W→T.The valueV(w,□φ) is defined as∧{R(w,u)⇒v(u,φ) ：u ∈W}where⇒is a relative pseudo-complement implication.Fitting’s many-valued modal logic is a monomodal many-valued logic,and the value set of formulas coincides with that of relations in a frame.

In the present work,we assumes that the set of valuesQis an inversely wellordered(or dually well-ordered)set,i.e.,every nonempty subset ofQhas a maximal element.Formally,a partialQ-valued frame is a pair(W,σ)whereW∅is a set of states andσ：W ×W→Qis a partial function.Ifσis a total function,one obtains totalQ-valued frames.In general,σ(w,u)=a(if exists)means thatuis accessible fromwbya.Each valuea ∈Qcan be interpreted in practical scenarios as an agent,and hence the relation={〈w,u〉：σ(w,u)exists and it is aboveainQ}is used to interpret the modality[a].A modal formula[a]φstates thata makes surethatφ.In general,since the values inQare ordered by≤,one could require that[b]φholds ifa ≤band[a]φholds.The agent with higher level has the ability to achieve what agents with lower level can do.Concrete scenarios where such frames can be used for modeling are not discussed in the present work.What we shall present contains a general framework for the study of multimodal logic and some related normal modal logics.This framework certainly differs from Fitting’s many-valued modal logic.

This article is structured as follows.Section 2 gives the modal language and semantics where partialQ-valued frames are introduced.Section 3 introduces normalQ-modal logics and proves the completeness of the minimal normalQ-modal logic.Section 4 defines some model constructions and proves some preservation results.Section 5 presents a Goldblatt-Thomason theorem for characterizing the modal definability of certain classes of partialQ-frames by the duality between partialQvalued frames and modalQ-algebras.Section 6 makes more observations on normalQ-modal logics and proves some general results.Section 7 gives concluding remarks.

2 Language and Semantics

The cardinal of a setXis denoted by|X|.In the present work,we assume the axiom of choice,and hence admit the well-ordering theorem,i.e.,for every setXthere exists a binary relation which well-ordersX.Aninversely well-ordered set(‘i.w.oset’for short)is a pair(Q,≤)such that≥well-orders the nonempty setQ,i.e.,≤is a linear order onQsuch that every subset ∅／X ⊆Qhas a maximal element∨X.The minimal element ofXis denoted by∧Xif it exists.Everyi.w.osetQhas the top element 1.IfQis finite,everya ∈Q{1}has a unique proper successora*.Adownsetin ani.w.osetQis a subsetX ⊆Qsuch thata ≤b ∈Ximpliesa ∈X.AnupsetinQis a subsetX ⊆Qsuch thata ∈Xanda ≤bimplyb ∈X.Let↓Xand↑Xbe the downset and upset inQgenerated byXrespectively.

Definition 1.LetQbe ani.w.oset.The multimodal languageLM(Q)consists of a denumerable set of propositional variables P={pi：i ＜ω},connectives⊥and→,and unary modal operators{[a]：a ∈Q}.The set of formulasFm(Q)is defined inductively as follows:

wherep ∈P anda ∈Q.Connectives⊤,¬,∧,∨and↔are defined as usual.For everya ∈Q,one defines〈a〉φ：=¬[a]¬φ.Thecomplexityof a formulaφ ∈Fm(Q),denoted byδ(φ),is defined inductively as follows:

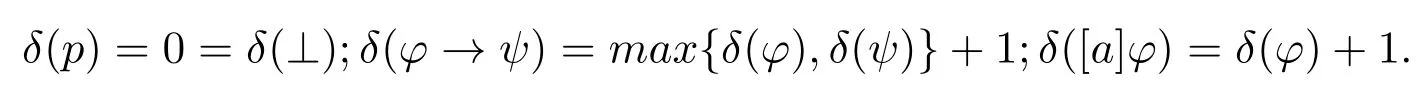
Asubstitutionis a functions：P→Fm(Q).For every formulaφ ∈Fm(Q),letφsbe obtained fromφby the substitutions.

Definition 2.LetQbe ani.w.oset.Amultivalued frame over Q(‘Q-frame’ for short)is a pair F=(W,σ)where∅is a set of states,andσ：W ×W→Qis a partial function fromW ×WtoQ.AnQ-frame F=(W,σ)is calledtotal,ifσis total,i.e.,every pair inW ×Wis defined.

Let F=(W,σ)be aQ-frame.The notationσ(w,u)!means thatσ(w,u)exists inQ.One writesσ(w,u)!≥aifσ(w,u)!andσ(w,u)≥a.For everya ∈Q,the binary relationonWis defined as follows:

Let(w)={u ∈W：σ(w,u)!≥a}.LetFQbe the class of allQ-frames.

Avaluationin aQ-frame F=(W,σ)is a functionV：P→P(W)from P to the powerset ofW.AQ-modelis a triple M=(W,σ,V)where(W,σ)is aQ-frame andVis a valuation in(W,σ).

Example 1.Consider the followingQ-frames F1and F2:

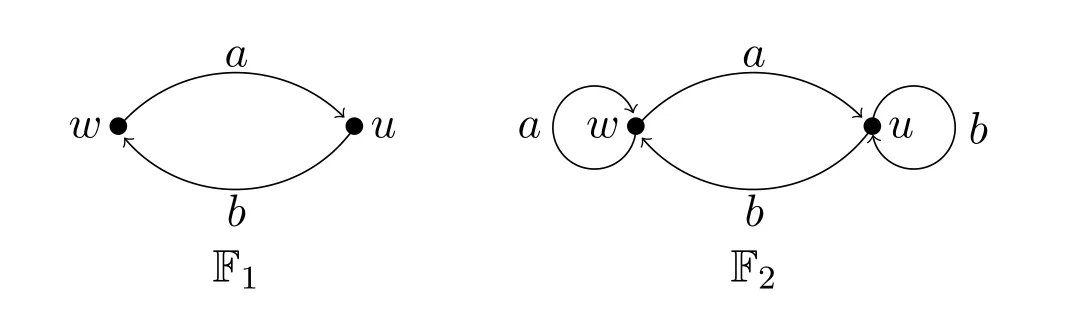
Here F1is not total sinceσ(w,w)andσ(u,u)are undefined.But F2is total.

Definition 3.Let F=(W,σ)be aQ-frame,M=(W,σ,V)aQ-model andw ∈W.For everyφ ∈Fm(Q),thesatisfaction relationM,w |=φis defined inductively as follows:

3 Normal Q-modal Logics and Completeness

In this section,we introduce normalQ-modal logics.As expected,the canonical method is applied in showing the completeness of the minimal normalQ-modal logic.

Definition 4.Anormal Q-modal logicis a set of formulasL ⊆Fm(Q)such thatLcontains the following formulas:

(Tau)All instances of classical propositional tautologies.

(Ka)[a](p→q)→([a]p→[a]q).

(CQ)[a]p→[b]p,wherea ≤binQ.

andLis closed under the following rules:

(MP)ifφ,φ→ψ ∈L,thenψ ∈L.

(Gen)ifφ ∈L,then[a]φ ∈L.

(Sub)ifφ ∈L,thenφs ∈Lfor every substitutions.

A formulaφis atheoremofL,notation⊢L φ,ifφ ∈L.

For every family of normalQ-modal logics{Li：i ∈I},∩i∈I Liis a normalQ-modal logic.TheminimalnormalQ-modal logic is denoted by KQ.Let ⊕

i∈I Libe the smallest normalQ-modal logic containing ∪i∈I Li.For every set of formulas Σ,let KQ ⊕Σ=∩{L：Σ⊆L},the minimal normalQ-modal logic containing Σ.If Σ={φ},we write KQ ⊕φinstead of KQ ⊕{φ}.For every normalQ-modal logicL,let NExt(L)be the set of all normalQ-modal logics containingL.

Remark 1.If|Q|=1,KQis exactly the standard monomodal logic with a single modality □(e.g.,[2]).Notions for basic normal modal logic can be applied.If|Q|＞1,one obtains multimodal logics with respect toQ.Moreover,the following hold for every normalQ-modal logicL:

(1)[a]⊤↔⊤∈Land〈a〉⊥↔⊥∈L.

(2)[a](φ1∧...∧φn)↔([a]φ1∧...[a]φn)∈L.

(3)〈a〉(φ1∨...∨φn)↔(〈a〉φ1∨...〈a〉φn)∈L.

(4)[a]φ∧〈a〉ψ→〈a〉(φ∧ψ)∈L.

(5)ifφ→ψ ∈L,then[a]φ→[a]ψ ∈Land〈a〉φ→〈a〉ψ ∈L.

LetLbe a normalQ-modal logic.A formulaφis aL-consequenceof a set of formulas Γ,notation Γ⊢L φ,ifφ ∈Lor there existψ1,...,ψn ∈Γ withψ1∧...∧ψn→φ ∈L.A set of formulas Γ isL-consistent,if Γ;and Γ ismaximal L-consistent,if Γ isL-consistent and⊆-maximal.One obtains the deduction theorem and Lindenbaum-Tarski lemma forL:(i)Γ,φ ⊢L ψif and only if Γ⊢L φ→ψ;(ii)if Γ isL-consistent,there is a maximalL-consistent set Σ with Γ⊆Σ.

A normalQ-modal logicLiscomplete,ifL=Th(FrQ(L)).One can obtain some completeness results using the canonical method.

Definition 5.LetWLbe the set of all maximalL-consistent sets of formulas.For everya ∈Q,one definesas follows:

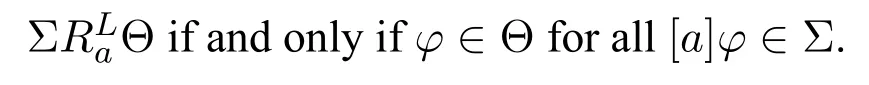
For every pair〈Σ,Θ〉 ∈WL ×WL,one defines(Σ,Θ)={a ∈Q：

Thecanonical Q-modelforLis defined as ML=(WL,σL,V L)where

andV L(p)={Σ∈WL：p ∈Σ}for everyp ∈P.Thecanonical Q-frameforLis defined as FL=(WL,σL).

Lemma 1.For everyΣ,Θ∈WL and a ∈Q,the following hold:

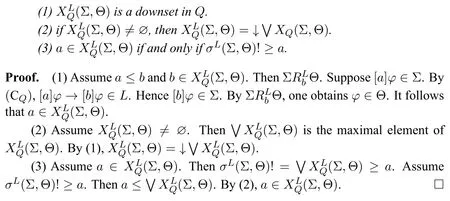
Lemma 2.For everyΣ∈WL,if[a]Σ,there existsΘ∈WL with a ∈Θ.

Proof.Assume[a]Σ.Let Γ={ψ：[a]ψ ∈Σ}∪{¬φ}.Assume that Γ is notLconsistent.Then Γ⊢L ⊥.There existψ1,...,ψn ∈Γ with(ψ1∧...∧ψn)→φ ∈L.By(Gen),(Ka)and(MP),[a](ψ1∧...∧ψn)→[a]φ ∈L.By[a](ψ1∧...∧ψn)↔([a]ψ1∧...[a]ψn)∈L,one obtains[a]φ ∈L.Then[a]φ ∈Σ,which contradicts the assumption.Hence Γ isL-consistent.Let Γ⊆Θ∈WL.Thena ∈andΘ. □

Lemma 3.For everyΣ∈WL,ML,Σ|=φ if and only if φ ∈Σ.

Theorem 1.KQ is complete.

Proof.Clearly Fr(KQ)=FQ.Obviously KQ ⊆Th(FQ).AssumeKQ.Then{¬φ}is KQ-consistent.Let Σ∈WKQwith¬φ ∈Σ.By Lemma 3,ML,Σ／|=φ.HenceTh(FQ). □

4 Model Constructions and Preservation Results

As far as modalQ-definability ofQ-frames concerned,one can define some interesting properties ofQ-frames.For example,letQbe finite.For everya ＜1,consider the property Φ(a):for every statewthere existuwithσ(w,u)=aand novwithσ(w,v)＞a.Clearly Φ(a)is defined by the formula〈a〉⊤∧[a*]⊥wherea*is the successor ofainQ.For more general results on the modalQ-definability of frames inLM(Q),one needs some preservation results onQ-frames.

Definition 6.Thedisjoint unionof a family ofQ-frames{Fi=(Wi,σi) ：i ∈I}is defined as ⊎i∈IFi=(W,σ)whereW=∪i∈I(Wi×{i})andσ：W ×W→Qis defined as follows:

Proof.One obtains(1)immediately by induction on the complexityδ(φ).The proof is omitted.Obviously(2)follows from(1). □

By Proposition 1,every modallyQ-definable class of partialQ-frames is closed under taking disjoint unions.It follows that the class of all totalQ-frames isnotmodallyQ-definable since it is certainly not closed under taking disjoint unions.The disjoint union of more than two totalQ-frames(Q-models)must be partial and not total.

Definition 7.Let F=(W,σ)be aQ-frame.For every ∅,thesubframeof F generated byXis theQ-frame FX=(WX,σX)where(i)WXis the smallest subset ofWcontainingXsuch thatσ(w,u)!impliesu ∈WXwheneverw ∈WXandu ∈W;and(ii)σX=σ∩(WX×WX).IfX={v},one writes Fv=(Wv,σv).AQframe F′=(W′,σ′)is agenerated subframeof F,if F′=FXfor some ∅.AQ-model M′=(F′,V ′)is agenerated submodelof aQ-model M=(F,V),if F is a generated subframe of F′andV(p)=V ′(p)∩Wfor everyp ∈P.One uses S ↣S′to denote that S is isomorphic to a generated substructure of S′.

Proposition 2.LetM=(F,V)andM′=(F′,V ′)be Q-models.AssumeM ↣M′.For every w ∈W and formula φ ∈Fm(Q),(1)MM′,w φ;and(2)ifF′ φ,thenF

Proof.One obtains(1)immediately by induction on the complexityδ(φ).The proof is omitted.Obviously(2)follows from(1). □

Definition 8.Let F=(W,σ) and F′=(W′,σ′) beQ-frames.A functionη：W→W′is abounded morphismfrom F to F′,if the following conditions hold for allw,u ∈W,u′ ∈W′anda ∈Q:

(1)ifσ(w,u)!≥a,thenσ(η(w),η(u))!≥a.

(2)ifσ′(η(w),u′)!≥a,there existsu ∈Wwithσ(w,u)!≥aandη(u)=u′.ForQ-models M=(F,V)and M′=(F′,V ′),a functionη：W→W′is abounded morphismfrom M to M′,ifηis a bounded morphism from F to F′and the following condition holds for allw ∈Wandp ∈P:

(3)w ∈V(p)if and only ifη(w)∈V ′(p).

AQ-frame F′is called abounded morphic imageof F,notation F ↠F′,if there exists a surjective bounded morphism from F to F′.

Example 3.Let{a1,...,an} ⊆Qwithai ≤ajfor 1≤i ≤j ≤n.Let F=(W,σ)and F′=(W′,σ′)beQ-frames where(i)W={wi：i ≤n}andσ(w0,wi)=ai;(ii)W′={u,v}andσ′(u,v)=an.

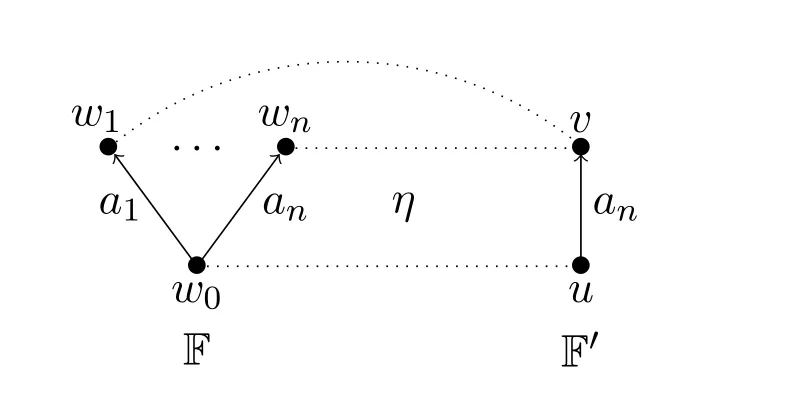
Letη：W→W′be the function withη(w0)=uandη(wi)=vfor all 1≤i ≤n.Note thatσ′(u,v)=an ≥aifor all 1≤i ≤n.It is quite easy to observe thatηis a surjective bounded morphism from F to F′.

Proposition 3.LetF=(W,σ)andF′=(W′,σ′)be Q-frames,andM=(F,V)andM′=(F′,V ′)be Q-models.Assume that η：W→W′ is a bounded morphism fromMtoM′.For every w ∈W and formula φ ∈Fm(Q),(1)M,w |=φ if and only ifM′,η(w)FF′ φ.

Theultrafilter extensionof a partialQ-model M=(F,V) is defined as Mue=(Fue,V ue)whereV ue(p)={u ∈Wue：V(p)∈u}for everyp ∈P.

Proposition 4.LetF=(W,σ)be a Q-frame andM=(F,V)be a Q-model.For every u ∈Wue and formula φ ∈Fm(Q),(1)V(φ)∈u if and only ifMue,uand(2)ifFue

5 Goldblatt-Thomason Theorems

The Goldblatt-Thomason theorem for modal logic(e.g.,[2,8])applies the Birkhoff’s variety theorem in universal algebra to modal logic.In this section,we first show such theorem holds for finite transitiveQ-frames.Then we introduce modalQ-algebras for normalQ-modal logics,and establish a Goldblatt-Thomason theorem for inversely well-ordered modal logic via the duality between modalQ-algebras andQ-frames.

Definition 10.AQ-frame F=(W,σ)istransitive,ifσ(w,u)!andσ(u,v)!implyσ(w,v)!for allw,u,v ∈W.LetT ＜ω Qbe the class of all finite transitiveQ-frames.A transitiveQ-frame F=(W,σ)isrooted,if there existsw ∈Wwithσ(w,u)!for allinW.Such a state is called therootof F.

LetQbe finite.A Goldblatt-Thomason theorem within the classcan be established by the Jankov-Fine formula for a rooted finite transitive frame as in basic modal logic(e.g.,[2,pp.143-144]).Let F=(W,σ)be a finite transitiveQ-frame with rootw=w0andW={w0,...,wn}.Each indexi ≤nis associated with a variablepi.Let∧Q=aand[a]+φ=φ∧[a]φfor every formulaφ.TheJankov-FineformulaφF,wis defined as the conjunction of the following formulas:

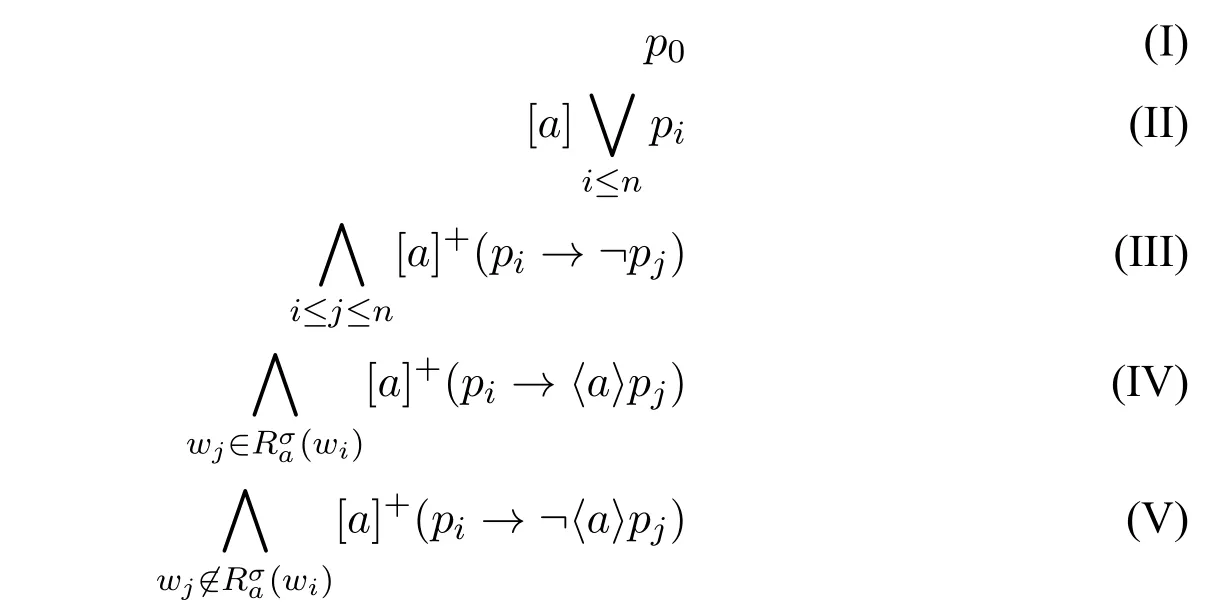
For every transitiveQ-frame G=(G,τ) andv ∈G,let Gv=(G′,τ′) be theQframe generated byv.

Lemma 5.Let Q be finite.For every transitive Q-frameG=(G,τ)and v ∈G,there exists a valuation U inGwithGF,w if and only if there exists a surjective bounded morphism η fromGv toFwith η(v)=w.

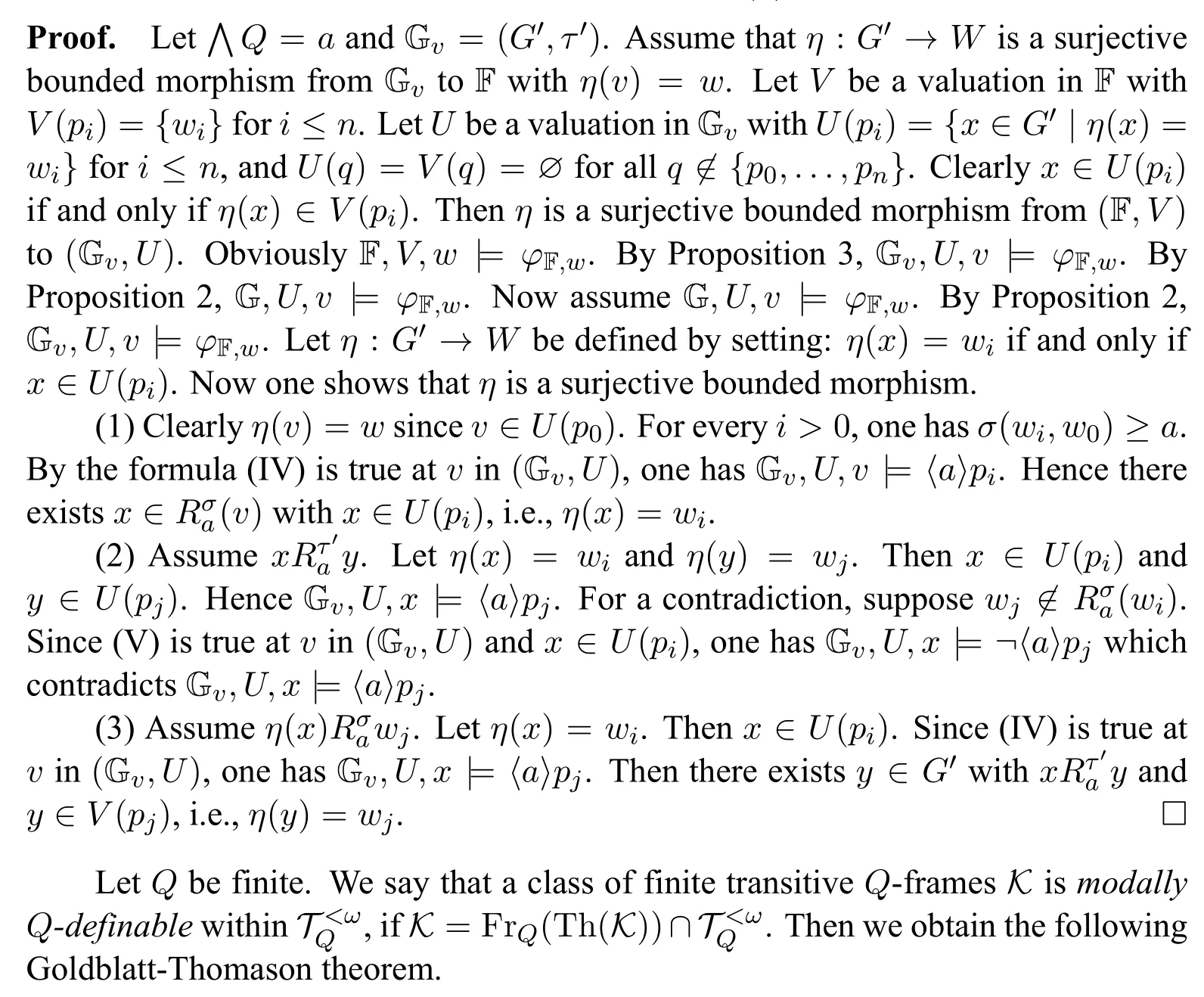
Theorem 2.Let Q be finite.A class of finite transitive Q-frames K ismodallyQdefinablewithinif and only if K is closed under taking disjoint unions,generated subframes and bounded morphic images.

Proof.The left-to-right direction follows from Proposition 1,Proposition 2 and Proposition 3.Conversely,assume thatKis closed under taking disjoint unions,generated subframes and bounded morphic images.We showK=FrQ(Th(K))∩ObviouslyK ⊆FrQ(Th(K))∩Assume that F∈and FTh(K).Let F=(W,σ).One has two cases:

Case 1.Suppose F has rootw.Obviously¬φF,w Th(K).There exists G∈Kwith GF,w.By Lemma 5,there existsvin G such that F is a bounded morphic image of Gv.Since G∈K,one has Gv ∈Kand so F∈K.

Case 2.Suppose F is not rooted.Clearly F is a bounded morphic image of the disjoint unionBy the proof of Case 1,one has Fx ∈Kfor everyx ∈W.It follows that F∈K. □

Now,for a more general Glodblatt-Thomason theorem,let us introduce modalQ-algebras for an arbitraryi.w.osetQand give some duality results.

Definition 11.LetQbe ai.o.wset.An algebra B=(B,+,-,0,♢a)a∈Qis amodal Q-algebra(‘Q-MA’for short),if(B,+,-,0)is a Boolean algebra and ♢ais a unary operator onBsatisfying the following conditions:

(1)♢a0=0.

(2)♢a(x+y)=♢ax+♢ay.

(3)♢bx ≤♢axifa ≤b.

One definesx·y=-(-x+-y),□ax：=-♢a -xand 1 ：=-0.One writes(B,♢a)a∈Qas aQ-MA whereBis supposed to be Boolean.

Fact 3.Let(B,♢a)a∈Qbe aQ-MA andx,y ∈B.The following hold:

(1)ifx ≤y,then ♢ax ≤♢ayand □ax ≤□ay.

(2)□a1=1 and □a(x·y)=□ax·□ay.

(3)ifa ≤b,then □ax ≤□bx.

Let F=(W,σ)be aQ-frame.Thecomplex algebraof F is defined as F+=It is quite easy to observe that F+is aQ-MA.For every class ofQ-framesK,let CmK={F+：F∈K}.

Definition 12.Let B=(B,♢a)a∈Qbe a finiteQ-MA.An elementx ∈Bis called anatom,ifx ／0,and 0≤y ＜ximpliesy=0.LetWBbe the set of all atoms in B.For everyx,y ∈WB,one defines

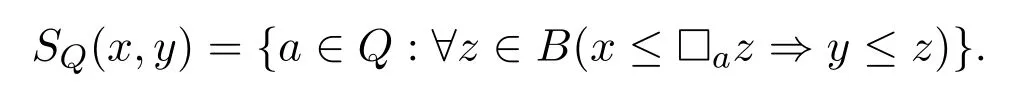
LetσB：WB ×WB→Qbe the partial function defined as follows:

TheQ-frame B·=(WB,σB)is called thedualof B.

Proposition 5.B～=(B·)+for every finite Q-MAB.

Proof.Let B=(B,♢a)a∈Q.One definesη：B→P(WB)by setting

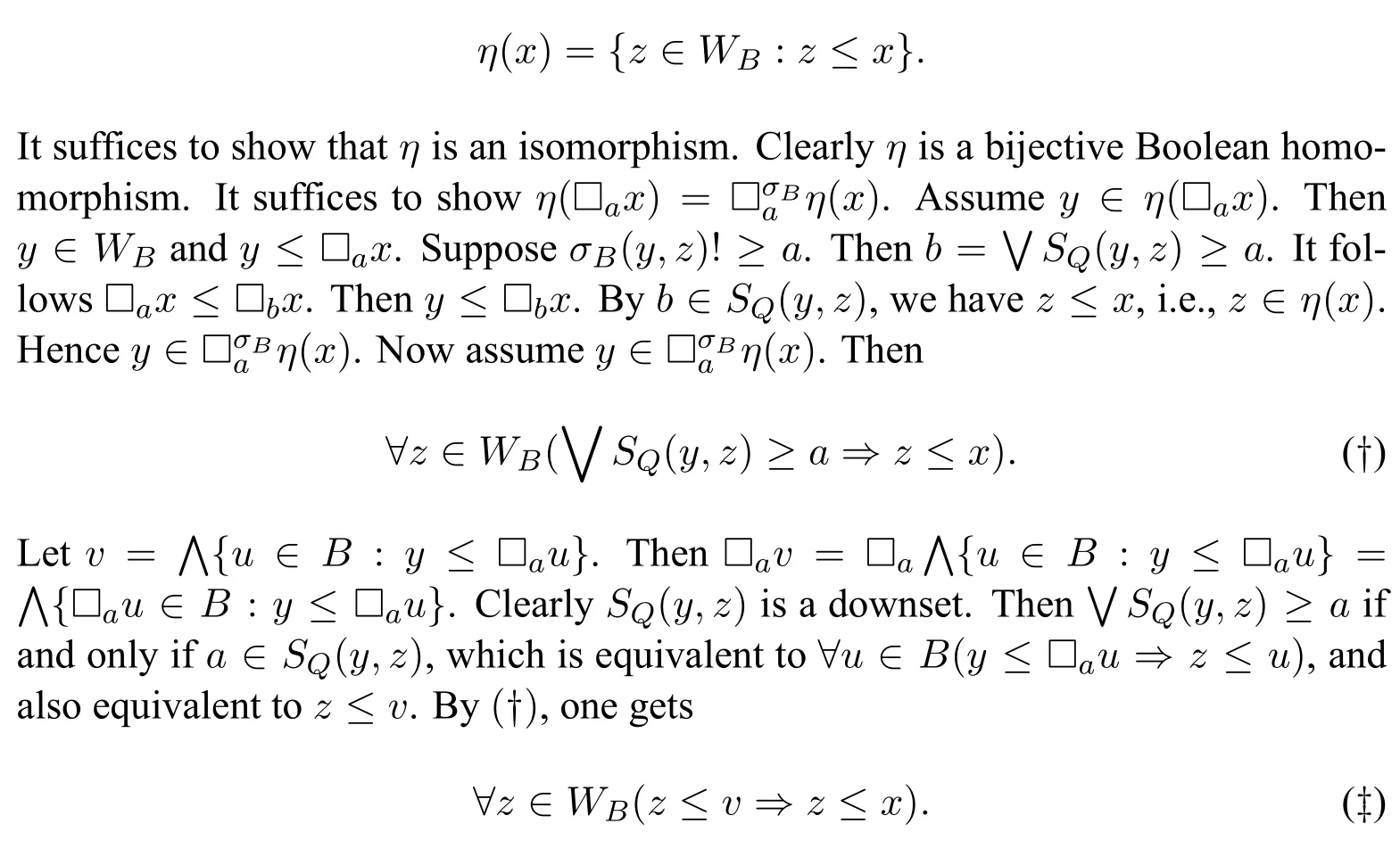
By(‡),v ≤x.Then □av ≤□ax.Clearlyy ≤□av.Hencey ≤□ax. □

Definition 13.Let B=(B,♢a)a∈Qbe aQ-MA.LetBufbe the set of all ultrafilters inB.For everyu,v ∈Buf,one defines

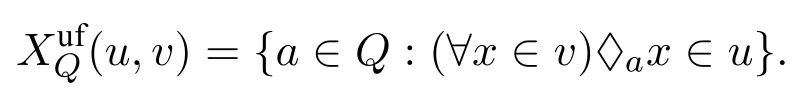
The partial functionσuf：Buf×Buf→Qis defined by:

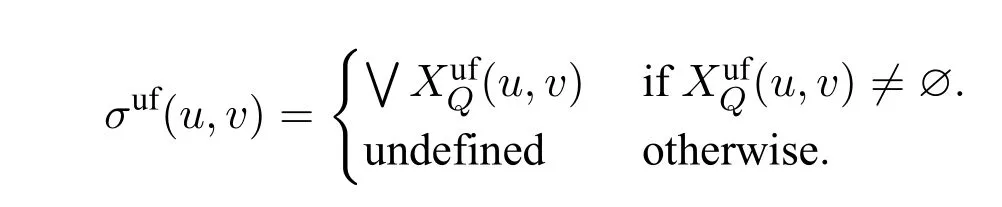
TheQ-frame B+=(Buf,σuf)is called theultrafilter frameof B.

Obviously,for everyQ-frame F,(F+)+=Fue.Moreover,the following Jónsson-Tarski representation theorem holds forQ-MAs.

Theorem 4.B ↣(B+)+for every Q-MAB.

Lemma 7.LetF=(W,σ)andG=(W′,σ′)be Q-frames,and η：W→W′ be a bounded morphism fromFtoG.Then(1)η+is a homomorphism fromG+toF+;(2)if η is injective,then η+is surjective;and(3)if η is surjective,then η+is injective.

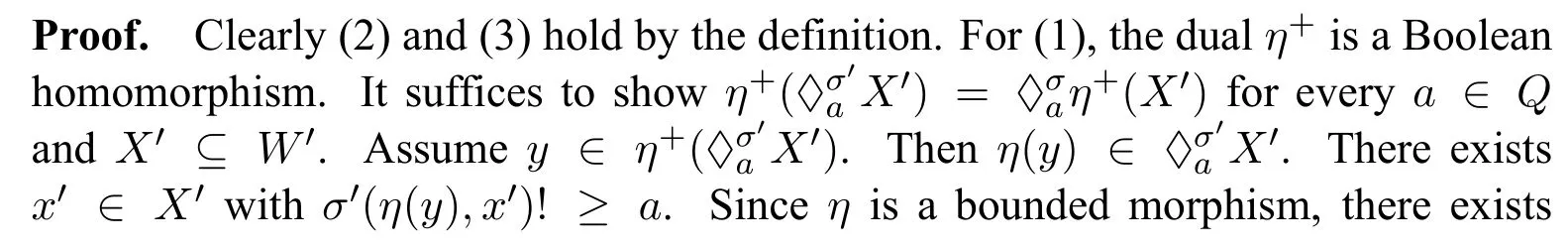
Lemma 9.LetFandGbe Q-frames,BandCbe Q-MAs.Then(1)ifF ↣G,thenG+↠F+;(2)ifF ↠G,thenG+↣F+;(3)ifB ↣C,thenC+↠B+;and(4)ifB ↠C,thenC+↣B+.

Proof.Straightforward by Lemma 7 and Lemma 8. □

Theorem 5.Let Q be ai.w.oset and K be a class of Q-frames which is closed under taking ultrafilter extensions.Then K is modally Q-definable if and only if it is closed under taking disjoint unions,generated subframes,bounded morphic images,and reflects ultrafilter extensions.

6 More Observations on Normal Q-modal Logics

In section 3,we introduce normalQ-modal logics and apply the canonical method to prove the completeness of the minimal normalQ-modal logic.In this section,we will make some particular observations on these logics.

A normalQ-modal logic iscanonical,if FL ∈FrQ(L).Obviously every canonical normalQ-modal logic is complete.As the Sahlqvist theorem for modal logic(e.g.,[2]),one obtains Sahlqvist normalQ-modal logics which are elementary and complete.The statement of elementarity needs an appropriate first-order language for talking about properties ofQ-frames.A choice is the first-orderQ-frame language with identityconsists of binary relational symbols{Ra：a ∈Q}where eachRais interpreted asσ(w,u)!≥ain aQ-frame F=(W,σ).

Table 1 :Some correspondence results

A formulaφ ∈Fm(Q)corresponds a sentenceαinif FrQ(φ)is defined byα.The correspondence between modal and first-order sentences in Table 1 can be shown immediately.One can defineSahlqvist formulasexactly as in e.g.,[2].Every Sahqvist formulaφinFm(Q)has a correspondentαφinthat is computed automatedly.ASahlqvist Q-modal logicis KQ ⊕Γ where Γ is a set of Sahlqvist formulas.One can show as usual that every SahlqvistQ-modal logic is canonical and hence complete(e.g.,[2]).

Next we make observations on the modal logics of singletonQ-frames.In the standard normal monomodal logic,there are only two singleton frames the logics of which are Post complete(e.g.,[4,12]).This is a direct consequence of Makinson’s classification theorem([10]).In the setting of normalQ-modal logics with|Q| ＞1 the situation is different.Let·be theQ-frame({·},σ)withσ(·,·)undefined.Let°abe theQ-frame({°},σ)withσ(°,°)=a.A normalQ-modal logicLisconsistent,if FrQ(L)∅.

Proposition 6.Let a,b ∈Q and／X,Y ⊆Q.The following hold:

Definition 14.Let M=(W,σ,V)be aQ-model.A subsetU ⊆Wisdefinablein M,if there existsφ ∈Fm(Q)withU=V(φ).AQ-model M′=(W,σ,V ′)with a valuationV ′inWis called avariantof M.We say that M′is adefinable variantof M,ifV ′(p)is definable in M for eachp ∈P.

Lemma 10.SupposeΓ⊆Fm(Q)is closed under substitution.IfMΓ,thenM′Γfor every definable variantM′ofM.

Proof.Let M=(W,σ,V)be a model and MΓ.Letφ ∈Fm(Q)andφ′be the formula obtained fromφby substitutingψiforpiinφ,and M′=(W,σ,V ′)be theQ-model whereV ′(pi)=V(ψi)with 1≤i ≤n.By induction on the complexityδ(φ)one obtains thatw ∈V(φ′)if and only ifw ∈V ′(φ).One obtains M′Γ by the same proof as[5,Theorem 5]. □

Theorem 6.Let L ∈NExt(KQ)be consistent.The following hold:

(·).

(2)if〈a〉⊤∈L for some a ∈Q,then L ⊆Th(°b)for some b ∈Q.

Proof.(1) Assumefor everya ∈Q.Let ML=(WL,σL,V L) be the canonical model forL.Let Γ={[a]⊥：a ∈Q}.Now we show that Γ isLconsistent.Suppose not.Then ∨a∈X〈a〉⊤∈Lfor some finite ∅X ⊆Q.Let∧X=b.Clearly ∨a∈X〈a〉⊤→〈b〉⊤∈L.Then〈b〉⊤∈Lwhich contradicts the assumption.Hence Γ isL-consistent.Let Σ∈WLand Γ⊆Σ.Clearly there is no Δ∈WLwithσL(Σ,Δ)!.Let M=(W,σ,V)be the model generated from MLby Σ.Due to[a]⊥∈Σ for alla ∈Q,one obtains that=(W,σ)consists of a single state Σ withσ(Σ,Σ)undefined.Obviously M,Σ.Note thatLis closed under substitution.By Lemma 10,one obtains·∈FrQ(L),i.e.,L ⊆Th(·).

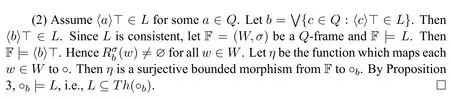
The notion of totalQ-frame is given in Definition 2.Here we consider a particular class of totalQ-frames.LetQ0be ani.w.oset with bottom element 0.Obviously every finite chain is certainly such ani.w.oset.The class of all totalQ0-frames is denoted byFQ0.Note that,althoughFQ0is not closed under taking disjoint unions,it is closed under taking generated subframes,bounded morphic images,and ultrafilter extensions.Moreover,Propositions 2,3 and 4 hold for totalQ0-frames.Now we introduce normal totalQ0-modal logics.

Definition 15.Anormal total Q0-modal logicis a set of formulasL ⊆Fm(Q0)

which contains(Tau),(Ka),(CQ0),and the following formulas:

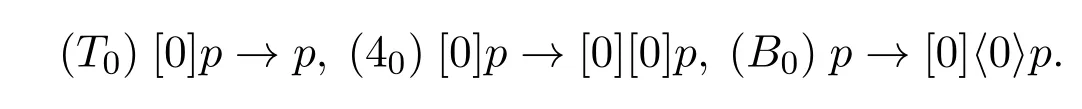
and is closed under(MP),(Gen)and(Sub).The minimal normal totalQ0-modal logic is denoted byLet NExt♭(L)be the set of all normal totalQ0-modal logics which containL.

Theorem 7.=Th(FQ0).

Proposition 7.For every consistent normal total Q0-modal logic L,there exists a ∈Q0with L ⊆Th(°a).

Proof.By〈0〉⊤∈Land Theorem 6,L ⊆Th(°a)for somea ∈Q0. □

Finally,we shall consider the embedding from a normalQ-modal logic to a normalQ′-modal logic whereQis embedded intoQ′in some way.In what follows,QandQ′are supposed to bei.w.osets.

Definition 16.Let(Q,≤Q,1)andbei.w.osets.A functionf：Q→Q′is anembedding,notationf：,iff(1)=1′and for alla,b ∈Q,a ≤Q bif and only iffafb.An embeddingf：isupward,iff(Q)is an upset inQ′.For everyf：,the functionεf：Fm(Q)→Fm(Q′) is defined inductively as follows:

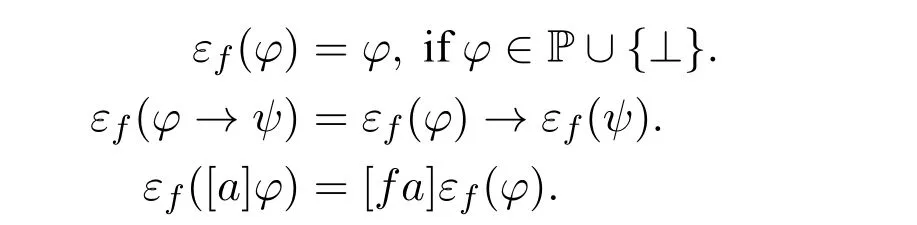
For every set of formulas Σ⊆Fm(Q),letεf(Σ)={εf(φ)：φ ∈Σ}.

Lemma 11.Let f：Σ∪{φ} ⊆Fm(Q),if φ ∈KQ ⊕Σ,then εf(φ)∈KQ′ ⊕εf(Σ).

Proof.Assumeφ ∈KQ ⊕Σ.The caseφ ∈Σ is obvious.Ifφis an instance of (Tau),by the definition ofεf,so isεf(φ).Ifφbe (Ka),thenεf(φ) is (Kfa).Suppose thatφis(CQ),i.e.,φ=[a]p→[b]pwitha ≤Q b.Then.Henceεf(φ)=[fa]p→[fb]p.Ifφis obtained by a rule(R)in KQ ⊕Σ,thenεf(φ)is also obtained by(R)in K(Σ). □

Letf：.For everyQ-frame F=(W,σ),one defines theQ′-frame Ff=(W,σf)by setting for allw,u ∈W:

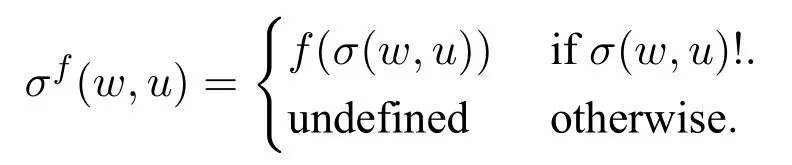
For everyQ-model M=(F,V),let Mf=(Ff,V).

Corollary 1.Let f：(Q),φ ∈KQ if and only if εf(φ)∈K

7 Concluding Remarks

In the present work we contribute new multimodal logics over multivalued frames.Multivalued frames over a set of valuesQare taken as the semantic ontology to interpret the corresponding multimodal language.We obtain Goldblatt-Thomason theorems for certain classes ofQ-frames.In the study of normalQ-modal logics,we adjust the canonical model method and obtain some completeness results.The logics of singleton frames and related Makinson’s classification theorem are established.There are many problems that are interesting for further exploration.Here we mention two of them:(i)throughout this paper,we considered onlyi.w.osets as organizations of agents.One could change the set of valuesQinto a (possibly distributive or Boolean) lattice in general,and study related problems;and (ii) try to give a Goldblatt-Thomason theorem which characterizes the modalQ-definability of certain classes of totalQ-frames.