The Complexity of Nilradicals and Jacobson Radicals in Computable Rings*

Xun Wang

Abstract.This paper expands upon the work by Downey et al.(2007),who proved that there are computable commutative rings with identity where the nilradical is -complete,and the Jacobson radical is -complete,respectively.We simplify the proof,showing that there is a computable commutative ring with identity where the nilradical is -complete and meanwhile the Jacobson radical is -complete.Moreover,we show that for any c.e.set A there exists a computable commutative ring with identity where the nilradical is Turing equivalent to A,and for any set B there exists a computable commutative ring with identity where the Jacobson radical is Turing equivalent to B.

1 Introduction

One of the most important questions to be studied in computable ring theory is the complexity of certain ideals.In this article we analyze two special ideals in computable rings.We mainly use computability theory to formulate and answer these complexity questions.Computability theory provides us hierarchies by which we can classify the complexity of certain mathematical objects,and techniques as well as methods by which to gauge them.

In particular,recently there has been a growing interest in the complexity of radicals in computable rings in terms of the arithmetical hierarchy.For example,Downey et al.([4])classified the complexity of the nilradical and Jacobson radical in commutative computable rings with identity,proving that the former is-complete,while the latter is-complete.Conidis([2])classified the complexity of the prime radical and Levitzki radical in computable noncommutative rings with identity,proving that the former is-complete,while the latter is-complete.In this paper,we expand upon the work by Downey et al.([4])and study the nilradical and Jacobson radical.

This paper focuses oncommutative rings with identity.Throughout the rest of this paper,by aringwe mean a commutative ring with identity.We collect here the important facts of commutative algebra that we will need.For general references on commutative algebra and ring theory,see[1,5,8].

Definition 1.Acomputable ringis a computable subsetR ⊆N equipped with two computable binary operations+and·onR,together with two elements 0,1∈Rsuch that(R,0,1,+,·)is a ring.

Throughout this paper,we useRto denote both the domain of the ring,as well as the tuple(R,0,1,+,·).

Definition 2.Anideal Iof a ringRis a subset ofR,which is an additive subgroup and is such thatRI ⊆I(i.e.,x ∈Randy ∈Iimplyxy ∈I).

We say an idealIinRismaximal,ifand there is no idealI′such thatI ⊂I′ ⊂R.We say an idealIinRisprime,ifand for anya,b ∈R,ab ∈Iimpliesa ∈Iorb ∈I.

Definition 3.An elementx ∈Risnilpotentifxn=0 for somen ＞0.

A nilpotent element is a zero-divisor(unlessR=0),but not conversely in general.

Definition 4.ThenilradicalofRis the set of all nilpotent elements inR.

For convenience,let Nil(R)denote the nilradical ofR.

Definition 5.TheJacobson radicalofRis the intersection of all the maximal ideals ofR.

For convenience,let Jac(R)denote the Jacobson radical ofR.

It is easy to verify the following propositions:

Proposition 1.Nil(R)is an ideal of R.

Proposition 2.Jac(R)is an ideal of R.

Now we introduce two special rings,the quotient ring and fraction field.Given a ringRand an idealIofR,for anyr ∈R,we call the set,r+I={r+i：i ∈I},acosetofIinR.And letR/I={r+I：r ∈R}.

Definition 6.LetRbe a ring andIbe an ideal ofR.We define the addition and multiplication onR/Ias follows:

(1) (a+I)+(b+I)=(a+b)+I

(2) (a+I)·(b+I)=(a·b)+I

Note thatR/Iwith the addition and multiplication is a ring.We callR/Ithequotient ring.

Definition 7.LetRbe any nonzero ring in which the product of any two nonzero elements is nonzero.Fora,b ∈Rwithb0,the fractiondenotes the equivalence class of pairs(a,b),where(a,b)is equivalent to(c,d)iffad=bc.Thefraction fieldofRis defined as the set of all such fractionsAnd we define the addition and multiplication on the fraction field as follows:

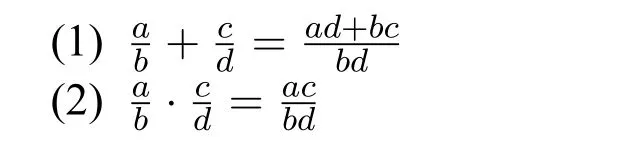
Note that the fraction field ofRwith the addition and multiplication is a ring.1The fraction field is not only a ring,but also a field.But here we do not need any results of field theory.

Definition 8.AunitinRis an elementx ∈Rwhich“divides 1”,i.e.,an elementxsuch thatxy=1 for somey ∈R.

The concept of unit will be used in the following characterization of the Jacobson radical.

Definition 9.Aring homomorphismis a mappingfof a ringAinto a ringBsuch that for allx,y ∈A,

(1)f(x+y)=f(x)+f(y)

(2)f(xy)=f(x)f(y)

Moreover,iffis a bijective homomorphism,thenfis called anisomorphismbetweenAandB,and ringsAandBare calledisomorphic.

We say a setarithmeticalif to define the set we are only allowed to quantify over number variables,but not set variables.The analytic hierarchy lies above the arithmetical hierarchy.We say a setanalyticif to define the set we are allowed to quantify over both number variables as well as set variables.Analytic sets are more complicated than arithmetical sets.From the computability-theoretic perspective,quantifying over sets can potentially lead to terribly complex objects.

By Definition 4,we have that:

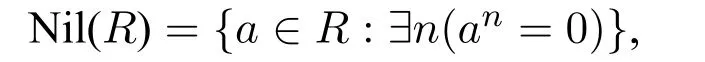
Obviously the nilradical is arithmetical.But the Jacobson radical is analytic since Definition 5 involves quantifying over maximal ideals of the ring,i.e.,over subsets of the ring.However,it is a standard result in commutative algebra that:

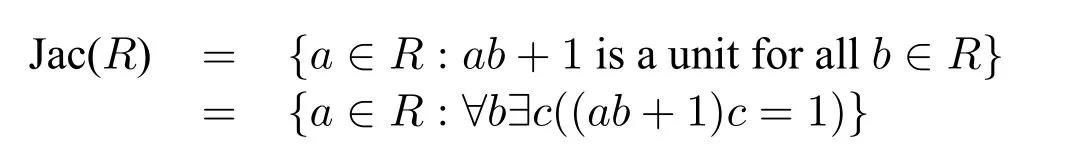
It follows that the Jacobson radical is also arithmetical,which means that we describe the Jacobson radical in a easier way than Definition 5.However,there is only one existential quantification on top of the operations in the definition of the nilradical.Further we could ask whether this characterization of the Jacobson radical is optimal in its quantifier complexity.For example,is it possible that there is a one quantifier description of the Jacobson radical using only existential quantification like the definition of the nilradical,or using only universal quantification? Or,is it possible that there is an∃∀-description of the Jacobson radical?

Downey et al.([4])have showed that the simplest characterization of the nilradical is just the standard definition,while the simplest characterization of the Jacobson radical is the∀∃-description above,by showing that the former is-complete while the latter is-complete.Arithmetical hierarchies and completeness are formally introduced in the next section.But intuitively,Γ-completeness means that:

(1) The complexity isΓ.

(2) Moreover,the complexity is maximal amongΓ-sets,i.e.,everyΓ-set can be reduced to aΓ-complete-set.

This paper is a continuation of[4]in which the authors construct two different rings to show the complexity of the nilradical and Jacobson radical,respectively.Our goal here is to simplify the proof by constructing a ring where the nilradical iscomplete and meanwhile the Jacobson radical is-complete.Moreover,we show that for any c.e.setAthere exists a computable ring where the nilradical is Turing equivalent toA,and for anysetBthere exists a computable ring where the Jacobson radical is Turing equivalent toB.

2 Preliminaries

In this section we give the reader basic background information about computability theory.For a general reference on computability theory,see[9].

We call a functionf：Nn→Ncomputableif there is a Turing machine that outputs the valuef()∈N on input∈Nn.Given a setA ⊆Nn,letCAdenote its characteristic function.We call a setA ⊆Nn computableif there is a Turing machine that outputsCA()∈{0,1}on input∈Nn.We call a setA ⊆Ncomputably enumerable,orc.e.,ifA=ØorA=ran(f)for some computable functionf.

We may also relativize notions of computability.For any setsA,B ⊆N,we say thatAiscomputable relative to B(writtenA ≤TB),if there is a Turing machine such that when given access to the functionCB,it outputsCA(x) on inputx ∈N.For any setsA,B ⊆N,we say thatAisTuring equivalenttoB(writtenA ≡TB),ifA ≤TBandB ≤TA.TheTuring degreeofA,or simplydegreeofA,is the equivalence classdeg(A)={B：B ≡TA}.Moreover,we writedeg(A)≤deg(B)to mean thatA* ≤TB*for some(any)A* ∈deg(A)and some(any)B* ∈deg(B).

Before introducing arithmetical hierarchies which will play a role below,we first give an example of how degrees can be used to describe the complexity of ideals.Consider this question:given a computable ringRand an elementainRbut not in Nil(R),how hard is it to find(or construct)a prime idealPofRsuch that?It is not sure that we could find a computable one.Naturally,we ask the following questions.Should any such prime idealPbe computable? Must there exist a such prime idealPwhich is computable? If the answer is negative,how high in the hierarchies of noncomputability must we need in order to observe such prime ideals? To answer these questions,we first introduce some related concepts.

Definition 10.We use 2＜Nto denote the set of all finite sequences of 0 and 1,partially ordered by the substring relation⊆.

Definition 11.(1)Atreeis a subsetTof 2＜Nsuch that for allσ ∈T,ifτ ∈2＜Nandτ ⊆σ,thenτ ∈T.

(2)Aninfinite pathorbranchof a treeTis a functionf：N→{0,1}such that for eachn ∈N we have that:

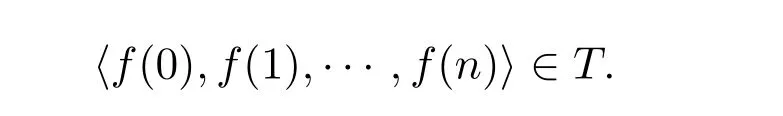
Proposition 3(Weak K¨onig’s Lemma).Every infinite tree has an infinite path.

Weak K¨onig’s Lemma is not“computably”true,in the sense that:

Proposition 4.There exists a computable tree T with no computable infinite path.

To characterize the degrees which compute solutions to Weak K¨onig’s Lemma,we introduce the following concept.

Definition 12.GivenA,B ∈N,we sayAisPA over Bif everyB-computable infinite tree has anA-computable infinite path.We say that a setAis ofPA degreeifAis PA over computable sets.

The following theorem relates PA degree to the complexity of prime ideals in computable rings.

Theorem 5(Friedman et al.,[6,7]).There exists a computable ring R such that every prime ideal P of R is of PA degree.

Theorem 5 shows that you need to look at least PA degree in order to ensure that you can find a prime ideal,partly answering our question about the complexity hierarchy that we need in order to find a prime ideal such that the prime ideal does not contain a particular element.

Next we complete the answer by proving that to find such a prime ideal,we need at most PA degree,showing that PA degree exactly captures the degree that you need in order to find such a prime ideal.

Theorem 6.Suppose that R is a computable ring and x is an element of R not in the nilradical.Then for every A of PA degree,there exists a prime ideal P of R such that deg(P)≤deg(A)2The proof borrows idea from[3].

Proof.Let{ai：i ∈N}be an enumeration ofR.We define a sequence of finite setsXσ ⊂R,σ ∈2＜N.LetXØ={0R}.Suppose thatXσhas been defined.Let

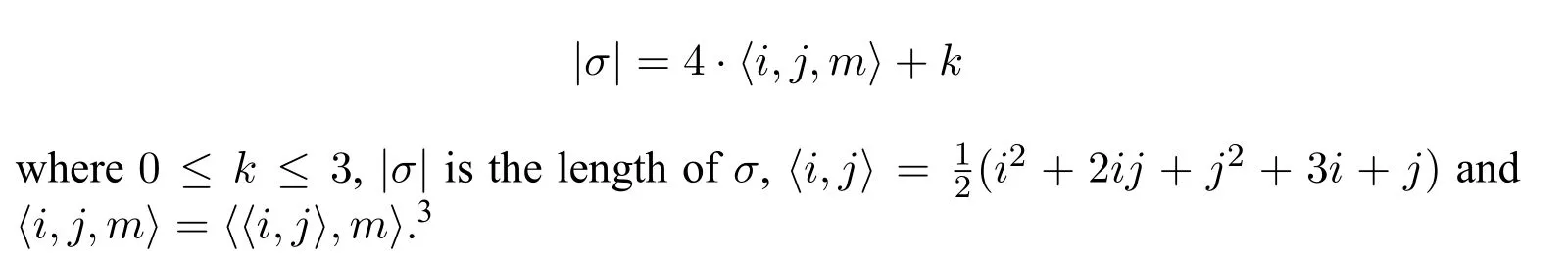
3Just note that〈i,j,m〉is a bijection between N3and N.It does not matter what is〈i,j,m〉.

·k=0.Ifai·aj ∈Xσ,setXσ0=Xσ ∪{ai}andXσ1=Xσ ∪{aj}.Otherwise,setXσ0=XσandXσ1=Ø.

·k=1.SetXσ0=Ø.Ifai,aj ∈Xσ,setXσ1=Xσ ∪{ai+aj}.Otherwise,setXσ1=Xσ.

·k=2.SetXσ0=Ø.Ifai ∈Xσ,setXσ1=Xσ ∪{ai·aj}.Otherwise,setXσ1=Xσ.

·k=3.SetXσ0=Ø.Ifxm ∈Xσ,setXσ1=Ø.Otherwise,setXσ1=Xσ.

LetS={σ：Xσ Ø}⊆2＜N.We have thatSis a computable tree.

Now we show that for eachm,n ∈N,there existsσ ∈Sof lengthnsuch thatxm〈Xσ〉where〈Xσ〉is the ideal ofRgenerated byXσ.Forn=0,the claim holds sincexm0 for allm ∈N.Forn ≡1,2,3 mod 4 and,obviously,if the claim holds fornthen it also holds forn+1.Suppose thatn ≡0 mod 4 and the claim holds forn.Next we show that it also holds forn+1.Letσ ∈Sbe of lengthn=4·〈i,j,m〉such thatxm〈Xσ〉for allm ∈N.Ifai·ajXσ,then the claim holds sinceXσ0=Xσ.Ifai ·aj ∈Xσ,we show that〈Xσ0〉=〈Xσ ∪{ai}〉and〈Xσ1〉=〈Xσ ∪{aj}〉do not both generate elements∈R.Assume for the sake of a contradiction that:

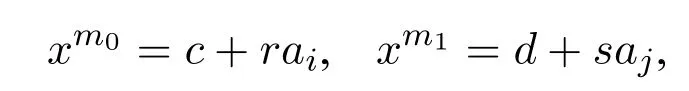
wherer,s ∈Randc,dare finite linear combinations of elements ofXσwith coefficients fromR.Then,

and so∈〈Xσ〉.4This relies on that R is a commutative ring.Note again that this paper only talks about commutative rings with identity.So we have a contradiction.Thus,xm〈Xσ0〉for allm ∈N,orxm〈Xσ1〉for allm ∈N.Therefore the claim holds forn+1.

We have thatSis infinite.LetA ⊆Nbe of PA degree.Then there exists anAcomputable infinite pathσ′inS.LetP=ThenP ≤TA.By the construction ofS,we have thatPis a prime ideal ofRandxP. □

Now we turn toarithmetical hierarchy,which will be used to classify the complexity hierarchy of the nilradical and Jacobson radical.We form the hierarchy of sets by alternating quantifiers.

Definition 13.Let natural numbersm,n ≥1.

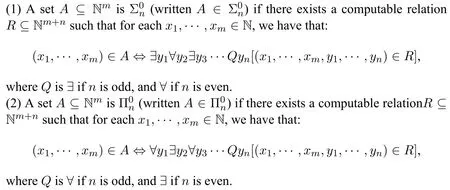
Proposition 7.A ⊆Nis computably enumerable(c.e.)iff A is

Definition 14.Aismany-one reducible(m-reducible)toB(writtenA ≤m B)if there is a computable functionfsuch thatf(A)⊆Bandfi.e.,x ∈Aifff(x)∈B.

Althoughm-reducibilityis the first and most natural reducibility,it is too restrictive.The reducibility≤Twe referred early is a more general concept,and we have that ifA ≤m B,thenA ≤TB.

3 The Nilradical and Jacobson Radical

Proposition 9(Downey et al.,[4]).If R is a computable ring,thenNil(R)is

Proof.We have that:

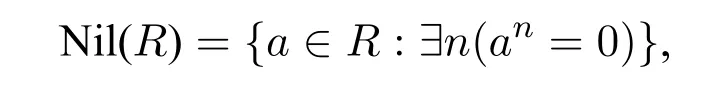
{(a,n)：an=0}is computable,so Nil(R)is□

Proposition 10(Downey et al.,[4]).If R is a computable ring,thenJac(R)is

Proof.We have that:

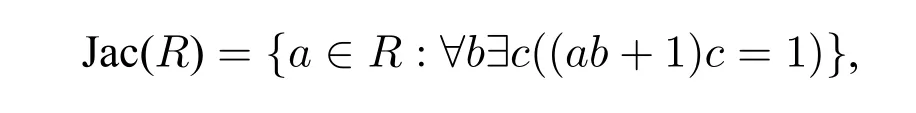
{(a,b,c)：(ab+1)c=1}is computable,so Jac(R)is□

In [4],the complexity of the two radicals in computable rings was studied.In particular,the following computability-theoretic results were established:

Theorem 11(Downey et al.,[4]).There exists a computable ring R such thatNil(R)is-complete.

Theorem 12(Downey et al.,[4]).There exists a computable ring R′such thatJac(R′)is-complete.

Theorem 11 shows that∃-description is optimal for the nilradical in its quantifier complexity,and Theorem 12 shows that∀∃-description is optimal for the Jacobson radical.However,in[4],the ringRconstructed for Theorem 11 and the ringR′for Theorem 12 are totally different.We next simplify the proofs of these two theorems by constructing one computable ring where the nilradical is-complete and meanwhile the Jacobson radical is-complete.Before proving the result,we first introduce two methods of building computable rings by taking subrings and quotient rings,which are very helpful for our proofs.5The methods are given by[4].

We first consider subrings.Suppose thatAis an infinite computable ring andSis an infinite c.e.subring ofA.We may viewSas a computable ringRin the following way.Note thatSis a c.e.subset ofA,then there exists a computable bijectionf：N→S.LetRbe the tuple(N,0,1,+,·)where 0R=f-1(0A)and 1R=f-1(1A),a+R b=f-1(f(a)+A f(b)) anda·R b=f-1(f(a)·A f(b)).Note thatRis a computable ring andfis a computable isomorphism betweenRandS,in a sense we could viewSas a computable ring.

We now consider quotient rings.Suppose thatAis a computable ring andIis a computable ideal ofA.We may realize the quotient ringA/Ias a computable ringRin the following way.LetRbe the set of minimal elements(with respect to the ordering on N) of cosets ofIinA.ThenRis computable.Define a functionh：A→Rby lettingh(a)be the unique element ofRsuch thata-h(a)∈I.We have thathis computable.Let the tuple(R,0,1,+,·)be such that 0R=h(0A)and 1R=h(1A),a+R b=h(a+A b)anda·R b=h(a·A b).Note thatRis a computable ring andhis a computable surjective homomorphism with kernelI,in a sense we could viewA/Ias a computable ring.

Combining the two methods,here we give a new method of building computable ring:

Lemma 1.Suppose that S is an infinite c.e.ring and J is a computable set such that S ∩J is an ideal of S.Then there exist a computable ring R and a computable surjective homomorphism h：S→R with kernel S ∩J,in a sense we could view S/(S ∩J)as a computable ring.

Proof.Sis an infinite c.e.ring,so we may realizeSas a computable ring as described before.There exists a computable bijectionf：N→S.LetS′=(N,0,1,+,·)where 0=f-1(0S)and 1S′=f-1(1S),a+S′ b=f-1(f(a)+S f(b))and=f-1(f(a)·S f(b)).We have thatS′is a computable ring andf：S′→Sis a computable isomorphism.LetI=f-1(S ∩J).We have thatS ∩Jis an ideal ofS.It is easy to see thatIis an ideal of.Iis computable,since

LetRbe the set of minimal elements(with respect to the ordering on N)of cosets ofIinS′.Note thatRis computable.Define a computable functionh：S→Rby lettingh(s)be the unique element ofRsuch thatf-1(s)-h(s)∈I.Let the ring(R,0,1,+,·)be such that 0R=h(0S)and 1R=h(1S),a+R b=h(f(a)+S f(b))anda ·R b=h(f(a)·S f(b)).We have thatRis a computable ring andhis a computable surjective homomorphism with kernelS ∩J. □

Proposition 13.Suppose that S/I is a quotient ring and R is a ring.Suppose that h：S→R is a surjective homomorphism with kernel I.6Indeed,even if h is not surjective,the proposition still holds.Then:a+I ∈Nil(S/I)iff h(a)∈Nil(R).

Proof.By definition of the nilradical,we have that:

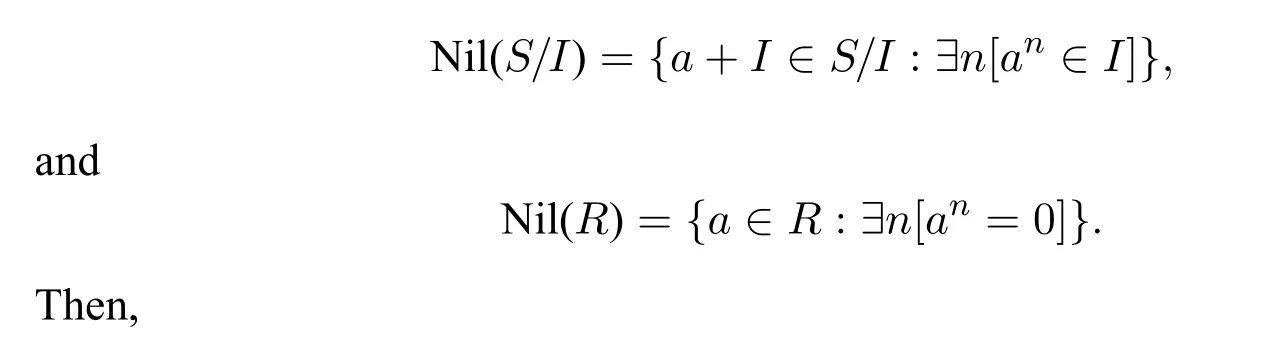
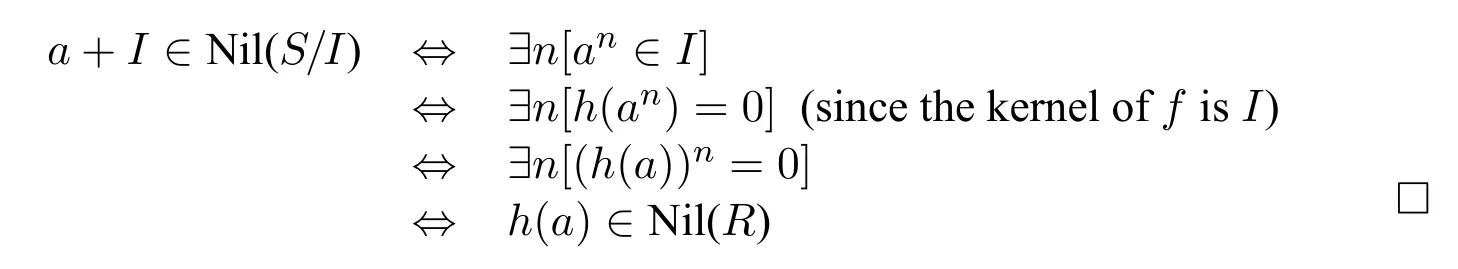
Proposition 14.Suppose that S/I is a quotient ring and R is a ring.Suppose that h：S→R is a surjective homomorphism with kernel I.Then:a+I ∈Jac(S/I)iff h(a)∈Jac(R).

Proof.By a standard result in commutative algebra,we have that:

We have thatσ(g)0,since the right-hand side is not 0.Thus the left-hand side has positiveyl-degree.However,the right-hand side hasyl-degree 0 becauseylpk.So we have a contradiction.Thus(xk+I)(yl+I)+(1+I)is not a unit inS/I.

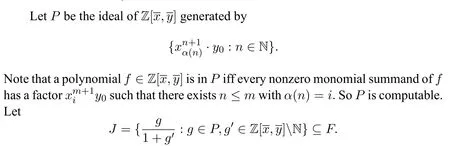
Note thatJis computable.We have thatI=S ∩J.Then as described in Lemma 1,we could realizeS/Ias a computable ringRand leth：S→Rbe the computable surjective homomorphism with kernelI.

Definef1：N→Rby lettingf1(k)=h(xky0) for allk ∈N.Sincehis computable,f1is computable.And we have that:

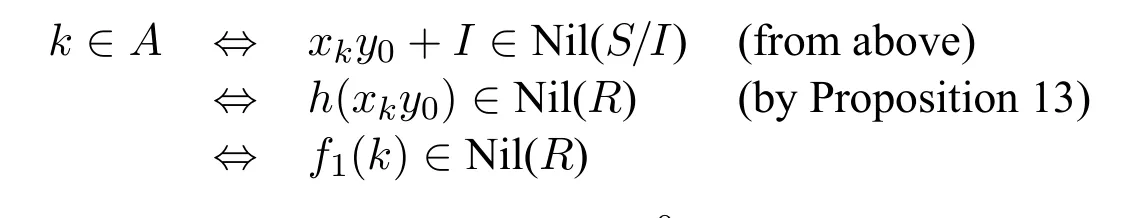
It follows thatA ≤mNil(R).Thus Nil(R)is-complete.

Definef2：N→Rby lettingf2(k)=h(xk)for allk ∈N.Sincehis computable,f2is computable.And we have that:

It follows that Inf≤mJac(R).Thus Jac(R)is-complete. □

Moreover,from Theorem 11 and Theorem 12 we immediately have the following corollaries:

Corollary 1.For any-complete(c.e.-complete)set A,there exists a computable ring R such thatNil(R)≡TA.

Corollary 2.For any-complete set A,there exists a computable ring R such thatJac(R)≡TA.

Next we prove more general results about the nilradical and Jacobson radical in computable rings.Let us start with the nilradical.

Theorem 16.For any c.e.set A,there is a computable ring R such thatNil(R)≡TA.7The proof borrows idea from[3].

Proof.Letαbe a computatble function with rangeA.LetIbe the ideal of Z[x]generated by

And,Nil(R)={f ∈R：∃n(fn=0R)}={f ∈R：∃n(fn ∈I)}={f ∈R:every nonzero monomial summand offhas a factorxisuch thati ∈A}.So Nil(R)≤TA. □

Now we turn to the Jacobson radical.

Theorem 17.For anyset A,there is a computable ring R such thatJac(R)≡TA.

Proof.Ais,so there is a computable relationPsuch thatx ∈A ⇔∀y∃zP(x,y,z).Bys-m-nTheorem8Please refer to[9].,define an injective computable functionfby