A Logic of von Wright’s Deontic Necessity*

Jie Fan

Abstract.In this paper,we build a bridge between G.von Wright’s deontic logic and E.Bezerra and G.Venturi’s ⊞-logic,in the sense that on one hand,we give an interpretation of⊞-operator as von Wright’s deontic necessity,and on the other hand,we give the exact semantics of von Wright’s deontic modalities.Inspired by an almost definability schema,we explain why the canonical model of the minimal ⊞-logic is defined in that way.We also present various axiomatizations of ⊞-logic,among which the transitive system is also inspired by the schema in question.We explain why the two non-equivalent semantics for ⊞involved in the literature,one of which is standard and the other is non-standard,come to give the same logic.We conclude with some discussions about notions of deontic non-contingency and deontic contingency.

1 Introduction

In his seminal work [20],von Wright investigates some logical properties of deontic concepts such as obligation,permission,and forbiddance.As von Wright observes,these concepts resemble the alethic ones—necessity,possibility,and impossibility—in many respects.

However,there is a crucial difference between the deontic concepts and alethic ones.Although every tautology is necessary,and every contradiction is impossible,this cannot be extended to obligation and forbidden.Von Wright suggests the following Principle of Deontic Contingency:a tautologous act is not necessarily obligatory,and a contradictory act is not necessarily forbidden.1This principle is formulated in terms of acts rather than propositions.However,a similar criterion can be defined for propositions,by simply replacing“act”with“proposition”in the formulation above.This criterion seems to be adopted by e.g.A.Prior([16])and E.Lemmon([12]).This means that,for instance,the semantics of obligation should be different from that of necessity.It is then natural to ask what the exact semantics is for these modalities.Unfortunately,to our knowledge,von Wright and his followers have not dealt with this issue yet.As we will argue below,among other similarities,the obligation operator□have the D schema,but no the necessitation rule,thus von Wright’s□should be understood as our ⊞operator,rather than the classical obligation operator(which will have the necessitation rule).

On the other hand,in a recent paper([1]),Bezerra and Venturi introduce a modality ⊞and present a minimal system of ⊞-logic.Semantically,⊞φis interpreted as“φis both necessary and possible”.According to the semantics,the ⊞-operator has many common properties with the serial necessity(that is,necessity over serial frames);2Maybe because of this fact,in an earlier version of[1],⊞is called the operator of serial necessity.for instance,K-andD-axioms are valid on the class of all frames,except for the failure of the necessitation rule.

However,the interpretation of ⊞is left open.This can be seen in the following paragraphs in[1,pp.8-9]:

As for the interpretation of the ⊞-operator,however,the matter is a bit more complicated.…As regards the failure of the necessitation rule,even though Lemmon argues that it is a desirable aspect of this logical system,this seems to go against the current state of deontic logics,where it is usually accepted that every tautology should be obligatory.

We leave the problem of the right interpretation of the ⊞-operator open.We just remark that if any can be found,this should be in a context where axiom(D⊞)plays a fundamental conceptual role and where the lack of necessitation does not cause harm to a faithful interpretation.

As we will demonstrate below,⊞-operator (and its dual) possesses all logical properties of the obligation modality (and its dual,permission) listed in [20].This may give an interpretation of ⊞-operator as the obligation in the previous sense,or as we will say,von Wright’s deontic necessity,on one hand,and also give the exact semantics of the deontic modalities in question,on the other hand.In doing so,we build a bridge between von Wright’s deontic logic and Bezerra and Venturi’s ⊞-logic.

Bezerra and Venturi’s work is connected to the pioneering work of Lemmon([12])on regular logics.Inspired by neighborhood semantics of regular logics,Lemmon proposes a Kripke semantics for ⊞(Lemmon uses a different symbol though),which involves a set of“normal”worlds and the usual truth-condition for the necessity operator□,see[13]and[17]for a systematic discussion of these logics and Sec.5 below.Rather than doing this,Bezerra and Venturi([1])introduce a non-standard semantics for ⊞,which involves a class of standard frames with a non-standard truth-condition—conjoined universal and existential—for□.It turns out the two semantics give the same logic.Although Bezerra and Venturi mention this,they do not attempt to explain why it should be so.In this paper,we will also give an explanation of it:the latter semantics is equivalent to the special case of the former in which the normal worlds are precisely those with successors.

Coming back to the minimal system given in [1],in order to show the completeness,the authors there adopt a canonical model construction.The construction contains a complicated definition of canonical relation,which though is not given any intuitive explanation,except for the statement that“The proof of completeness is inspired by[18]”([1],p.6).In the present paper,as in[7,8,4],we introduce a special almost definability schema,which says that ⊞φand□φare equivalent given some proposition.As we will see,with help of the schema,we will give an explanation of why the canonical relation is defined in that way.The schema also helps us find a complete axiomatization of transitive ⊞-logic.

The rest of the paper is organized as follows.Sec.2 introduces the syntax and semantics of von Wright’s deontic necessity,including the so-called deontic tautologies concerning obligation and permission operators in[20],and an almost definability schema of great importance.Sec.3 proposes the minimal system of deontic logic in the sense of von Wright’s deontic necessity and shows its completeness,where the canonical relation is inspired by the previous almost definability schema.It also includes an explication of why the canonical model in[1]is defined in that way.Sec.4 explores various extensions,where the transitive axiom is also inspired by the almost definability schema.Sec.5 briefly reviews the pioneering work of Lemmon and gives an explanation of why the two semantics give the same logic and an alternative proof of completeness of a system given in[17].We finally conclude in Sec.6 with some discussions on deontic non-contingency and deontic contingency.

2 Syntax and Semantics

Throughout the current paper,we fixPto be a nonempty set of propositional variables andp ∈P.

Definition 1.The languageL(□,⊞)is inductively defined as follows:

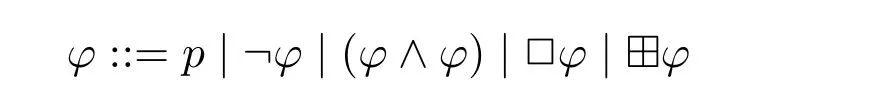
Without the construct ⊞φ,we obtain the languageL(□)of standard modal logic;without the construct□φ,we obtain the languageL(⊞)ofthe logic of von Wright’s deontic necessity.

Intuitively,□φis read“it is(alethic)necessary thatφ”,⊞φis read“it isobligatory(in the sense of von Wright)thatφ”,or“it isdeontically necessarythatφ”.Other connectives are defined as usual;in particular,◇and◇+are,respectively,the dual of□and ⊞.Formula◇+φis read“it ispermitted(in the sense of von Wright)thatφ”,or“it isdeontically possiblethatφ”.In the sequel,we will focus onL(⊞).

The above languages are interpreted over standard models.A standard model,or simplymodel,is a tripleM=〈S,R,V〉,whereSis a nonempty set of worlds,Ra binary relation onS,andVa valuation function for propositional variables.A(standard)frameis a model without valuations.Apointed modelis a pair of a model and a world in it.

Given a modelM=〈S,R,V〉and a worlds ∈S,the semantics ofL(□,⊞)is defined as follows.

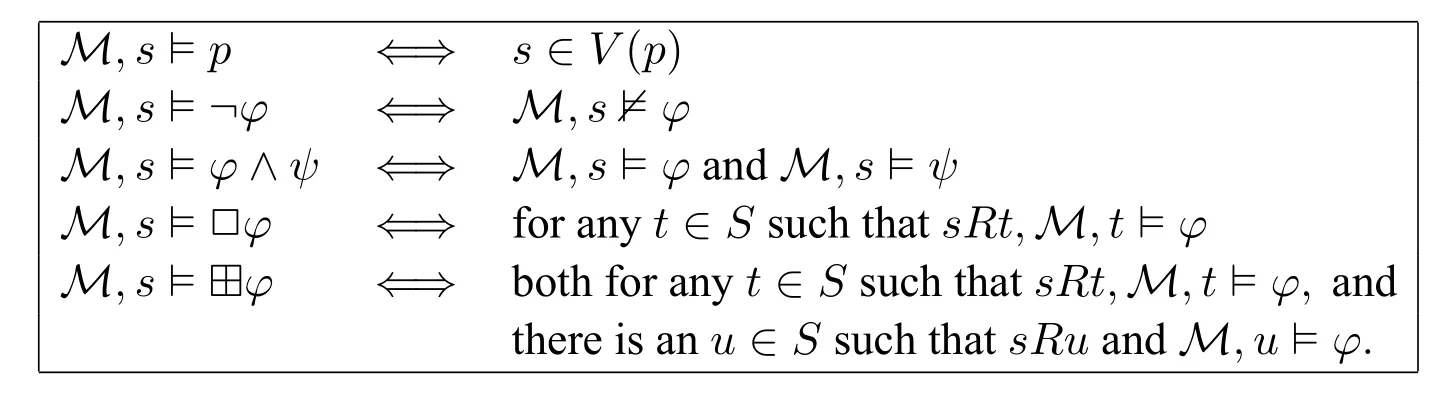
We say thatφistrueat the worldsin the modelM,ifM,s⊨φ;we say thatφisvalid on a model M,denotedM⊨φ,ifφis true at every world inM;we say thatφisvalid in a frame F,denotedF⊨φ,ifφis valid on every model based onF;we say thatφisvalid on a classCof frames,denoted C ⊨φ,ifφis valid on every frame in C.We say that (M,s) and (M′,s′) areL(⊞)-equivalent,denoted(M,s)≡(M′,s′),if for allφ ∈L(⊞),we have thatM,s⊨φiffM′,s′⊨φ.

As shown in[1,Prop.1.1],over serial models,□φand ⊞φare equivalent to each other.Also,one may easily verify that ⊞and□are interdefinable,since ⊨⊞φ↔(□φ∧◇φ)(also,⊨⊞φ↔(□φ∧◇⊤)),and ⊨□φ↔(⊞⊤→⊞φ).3This is suggested by Lloyd Humberstone in a private communication to Bezerra and Venturi,see[1,Footnote 1].Despite this interdefinability,we will propose an almost definability schema below (see Prop.2 and the remarks preceding it),which can help us find an explanation of why the canonical model in[1]is defined in that way,and also a desired axiom in axiomatizing L(⊞)over transitive frames.In contrast,the interdefinability in question cannot provide either of them,as one may check.

We have the following validities(that is,in von Wright’s terminology,deontic tautologies).About the deontic intuition of these formulas,we refer to[20,pp.13-14].4Here we replace O and P in[20]with ⊞and ◇+,respectively,and A,B,C there with φ,ψ,χ,respectively.Note that to avoid some parentheses,von Wright rules that“a deontic operator before a molecular complex of names of acts refers to the whole complex and not to its first constituent only”([20],p.5),e.g.,P A ∨B means P(A ∨B).This regulation is then cancelled in[19,Chap.5].

The following two laws concerns about the relation between obligation and permission.

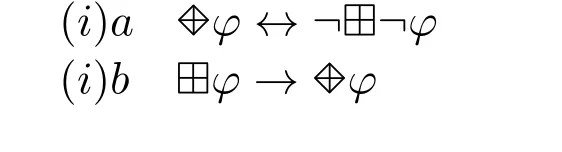
The following four laws concerns about the“dissolution”of deontic operators.

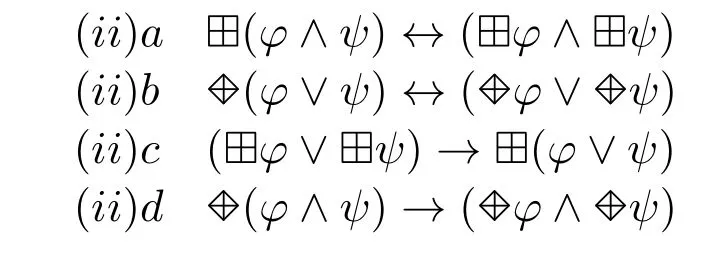
Here are seven laws on“commitment”.5Von Wright mistakenly counts the number of laws as six,but it is actually seven.Many people would find von Wright’s discussion of commitment to be quite implausible,and have developed dyadic deontic logics with an operator O(·/·)(“conditional obligation”)where the intended reading of O(φ/ψ)is“it ought to be that φ,given that ψ”.(See Example 4.4.4,p.241,in[10].)

As explained by von Wright,(iii)asays that if doing what we ought to do commits us to doing something else,then this new act is also something which we ought to do,(iii)bsays that if doing what we are free to do commits us to doing something else,then this new act is also something which we are free to do (in other words,doing the permitted can never commit us to doing the forbidden),(iii)csays that if doing something commits us to doing the forbidden,then we are forbidden to do the first thing,(iii)dsays that an act which commits us to a choice between forbidden alternatives is forbidden,(iii)esays that it is logically impossible to be obliged to choose between forbidden alternatives,(iii)fsays that if doing two things,the first of which we ought to do,commits us to doing a third thing,then doing the second thing alone commits us to doing the third thing,“Our commitments are not affected by our(other)obligations”,and(iii)gsays that if failure to perform an act commits us to performing it,then this act is obligatory.

We take the validity of (iii)aas an example,which is shown to be a deontic tautology in[20,p.12]by using the truth-value table method.

Proposition 1.⊞φ∧⊞(φ→ψ)→⊞ψ is valid.

Proof.Suppose,for reductio,that for some modelM=〈S,R,V〉and somes ∈S,we haveM,s⊨⊞φ∧⊞(φ→ψ)andM,s⊭⊞ψ.Theneitherthere is atsuch thatsRtandM,t⊭ψ,orfor anyusuch thatsRu,M,u⊭ψ.If the first case is true,fromM,s⊨⊞φ∧⊞(φ→ψ),we haveM,t⊨φ∧(φ→ψ),which implies thatM,t⊨ψ:a contradiction.If the second case is true,froms⊨⊞φ,it follows that there is anxsuch thatsRxandM,x⊨φ,and thusM,x⊭ψ,which entails thatM,x⊭φ→ψ,contrary to the fact thatM,s⊨⊞(φ→ψ)andsRx. □

One of our main interests is to understand the definition of the canonical model introduced in[1].The crucial observation is the following schema,which says that given some deontically necessary proposition,□is definable in terms of ⊞:

In this sense,we say that□isalmostdefinable with ⊞.Unlike the almost definability schemas in[7,8,4],in the current almost definability schema,ψonly occurs in the antecedent ⊞ψbut not in the consequent□φ↔⊞φ.This may be explained by the fact that□φand ⊞φare logically equivalent atany given pointwith a successor,which can be provided by any formula of the form ⊞ψ.In fact,the new schematic letterψdoes not need to appear at all since we can replace it(thanks to the monotony of ⊞)with⊤—but we still stick to useψrather than⊤because the former is more convenient in Remark 1.We leave the reader to check the following result.

Proposition 2.⊞ψ→(□φ↔⊞φ)is a validity of L(□,⊞).

3 Minimal Logic

3.1 Proof system

Definition 2.The minimal system K⊞consists of the following axiom schemas and inference rules:

Intuitively,the axiom ⊞D says that obligatory things are permitted,the axiom⊞∧says that the conjunction of two obligatory things is also obligatory,and the rule RM⊞concerns about the monotony of the obligation operator.

Notice that our proof system K⊞and the one in[1]only differs in that ⊞(φ→ψ)→(⊞φ→⊞ψ) (denoted K⊞there) is used there,whereas we use the axiom⊞∧.6The proof system in[1]is called D2 in[12]and CD in[17].The intention behind K⊞is presumably to have the form resembling the□-based axiom K.In comparison,the axiom ⊞∧is found to satisfy the need of the truth lemma(and thus the completeness proof)below.At the end of this section,we will give a syntactic proof of K⊞in our proof system.

The rule RM⊞is called RK⊞in [1].This,for us,is a bit confusing,in that it concerns about the monotony,rather than the normality,of the ⊞operator,compared with their□-counterparts in normal modal logics,usually denoted RM and RK,respectively,refer to e.g.[2,10].

Notions of derivability and theorems are defined as usual,and we use⊢φto denoteφis derivable in K⊞.

It is easy to show the following result.

Fact 1.The following rule,denoted RE⊞,is derivable in K⊞:

Recall that von Wright writes:

It should,however,be observed that if there really existed an act,sayA,which is such thatP(A&～A)expresses a true proposition,then every act would be permitted.([19,p.38])

This can be expressed in the languageL(⊞)as◇+(φ∧¬φ)→◇+ψ,7We thank an anonymous referee for this observation.which is derivable in K⊞from TAUT and RM⊞immediately.

3.2 Completeness

The proof of the completeness is based on a canonical model construction.

Definition 3.Thecanonical modelof K⊞is a tripleMc=〈Sc,Rc,V c〉,where

·Sc={s|sis a maximal consistent set for K⊞}.

·sRctiff there existsψsuch that(a)⊞ψ ∈sand(b)for allφ,if ⊞φ ∈s,thenφ ∈t.

·V c(p)={s ∈S |p ∈s}.

The above definition ofRcis inspired by the schema(⋆),namely ⊞ψ→(□φ↔⊞φ).Recall that in the construction of canonical model for the minimal normal modal logic,the canonical relationRcis defined such thatsRctiff for allφ,if□φ ∈s,thenφ ∈t.Now given the schema(⋆),□φ ∈scan be replaced with ⊞φ ∈sprovided that ⊞ψ ∈sfor someψ.Intuitively,if¬⊞χholds on a world for allχ,then so does¬⊞⊤,which implies thatsis a dead point.

Note that due to the absence ofψin the condition (b),the definition ofRcis equivalent to the following:

sRctiff(a)there existsψsuch that ⊞ψ ∈sand(b)for allφ,if ⊞φ ∈s,thenφ ∈t.

Remark 1.One may easily verify that our definition ofRcis equivalent to (but simpler than) the definition ofR⊞given in [1],where the canoical modelM⊞=〈W⊞,R⊞,V⊞〉is defined as follows:

1.W⊞={w | wis a maximal consistent set for K⊞}such thatW⊞=Ws ∪W¬swhere:

·w ∈Wsiff for someφwe have ⊞φ ∈w;

·w ∈W¬siff there is noφsuch that ⊞φ ∈w.

2.R⊞⊆W⊞×W⊞is defined as folows:for allw,y ∈W⊞,

· ifw ∈Ws,thenwR⊞yiffλ(w)⊆y,whereλ(w)={φ|⊞φ ∈w}.

· ifw ∈W¬s,then there is noy ∈W⊞such thatwR⊞y.

3.V⊞(p)={w ∈W⊞|p ∈w}.

In this way,with the help of the schema(⋆),we have given an explanation of why the canonical model in[1]is defined as above.

Defineη(s)={χ |⊞χ ∈s}fors ∈Sc.The following result lists some properties of the functionη,which say thatη(s) is closed under conjunction and logical deduction.This will be used in the proof of the truth lemma.

Proposition 3.

1.If φ,ψ ∈η(s),then φ∧ψ ∈η(s).

2.If φ ∈η(s)and ⊢φ→ψ,then ψ ∈η(s).

Proof.For 1,suppose thatφ,ψ ∈η(s),then ⊞φ,⊞ψ ∈s.By axiom ⊞∧,we infer that ⊞(φ∧ψ)∈s,and thereforeφ∧ψ ∈η(s).

For 2,assume thatφ ∈η(s) and⊢φ→ψ,then ⊞φ ∈s.Applying the rule RM⊞,we derive that⊢⊞φ→⊞ψ,and therefore ⊞ψ ∈s,that is,ψ ∈η(s). □

Now we are close to the demonstration of the truth lemma.

Lemma 1(Truth Lemma).For all s ∈Sc,for all φ ∈L(⊞),we have

Proof.By induction onφ.The only non-trivial case is ⊞φ.

Suppose that ⊞φ ∈s,to show thatMc,s⊨⊞φ.By induction hypothesis,it suffices to prove that(1)for allt ∈Sc,ifsRct,thenφ ∈t,and(2)there existsu ∈Scsuch thatsRcuandφ ∈u.(1)is immediate by the supposition and the definition ofRc.For(2),by Lindenbaum’s Lemma,it remains to demonstrate thatη(s)∪{φ}is consistent.

Ifη(s)∪{φ}is not consistent,we consider two cases.

·η(s)=Ø.Then⊢¬φ,and thus⊢φ→¬φ.Moreover,by supposition,we infer thatφ ∈η(s).Then by the item 2 of Prop.3,we derive that ⊞¬φ ∈s.

·η(s).Then there areχ1,···,χn ∈η(s)such that⊢χ1∧···∧χn→¬φ.By the item 1 of Prop.3,we haveχ1∧···∧χn ∈η(s).Then by the item 2 of Prop.3,we infer that¬φ ∈η(s),namely ⊞¬φ ∈s.

In either case,we have ⊞¬φ ∈s.However,by supposition and axiom ⊞D,we also have◇+φ ∈s,that is,¬⊞¬φ ∈s:a contradiction.

We have now shown thatη(s)∪{φ}is consistent,as desired.

Conversely,assume that ⊞,to prove thatMc,s⊭⊞φ.For this,suppose,to exploit the induction hypothesis,that there existsu ∈Scsuch thatsRcuandφ ∈u,to find at ∈Scsuch thatsRctand.For this,by Lindenbaum’s Lemma,we only need to show thatη(s)∪{¬φ}is consistent.

By supposition,it follows that there existsψsuch that ⊞ψ ∈s.This provides the non-emptiness ofη(s).Ifη(s)∪{¬φ}is not consistent,then as in the previous proof of the consistency ofη(s)∪{φ},we can obtain that ⊞φ ∈s,which is contrary to the assumption.

We have thus shown thatη(s)∪{¬φ}is consistent,as desired. □

As a corollary,we can obtain the relationship betweenshaving successors andscontaining some ⊞ψ.

Corollary 1.The following conditions are equivalent:

(1)s has an Rc-successor;

(2)s contains some⊞ψ.

Proof.The direction from (1) to (2) is immediate from the definition ofRc.The other direction follows from the proof of Lem.1. □

We claim that every K⊞-consistent set of formulas can be extended to a maximal K⊞-consistent set in the standard way(Lindenbaum’s Lemma).

With Lem.1 and Lindenbaum’s Lemma in hand,it is now a routine exercise to show the completeness of K⊞.

Theorem 1.K⊞is sound and strongly complete with respect to the class of all frames.

We conclude this section with a syntactic proof of K⊞in our system.

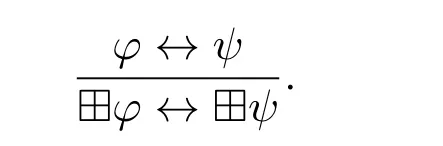
Proposition 4.⊢⊞(φ→ψ)→(⊞φ→⊞ψ).

Proof.We have the following proof sequences in K⊞:

4 Extensions

This part explores some extensions of K⊞over special frames and shows their completeness.First,define D⊞=K⊞+⊞⊤.

Theorem 2.D⊞is sound and strongly complete with respect to the class of serial frames.

Proof.The soundness follows from that of K⊞and the validity of ⊞⊤,where the latter is straightforward.

For completeness,by Thm.1,it suffices to show thatRcis serial.By axiom ⊞⊤,it remains to prove thatη(s)is consistent.

If not,then there areχ1,···,χm ∈η(s)such that⊢χ1∧···∧χm→⊥.Then by Prop.3,we can obtain that⊥∈η(s),that is,⊞⊥∈s.However,by axiom ⊞⊤and axiom ⊞D,◇+⊤∈s,that is,¬⊞⊥∈s:a contradiction. □

Define T⊞=D⊞+⊞T,where ⊞T denotes ⊞φ→φ.8It may be worth mentioning the difference between the axiom(schema)⊞T and the axiom ⊞⊤.Note that ⊞⊤is indispensable in T⊞,which is different from the case in normal modal logics T and D(recall that the seriality axiom D=□φ→◇φis derivable in T=K+T,where K is the minimal normal modal logic,and T=□φ→φ).To see the“indispensability”part,define an auxiliary semantics which interprets all formulas of the form ⊞φas⊥.One may easily verify that T⊞-⊞⊤is sound with respect to the auxiliary semantics,but ⊞⊤is not.

Theorem 3.T⊞is sound and strongly complete with respect to the class of reflexive frames.

Proof.The soundness is straightforward.For completeness,it suffices to prove thatRcis reflexive.That is,for alls ∈Sc,sRcs.

By axiom ⊞⊤,it suffices to prove that for allφ,if ⊞φ ∈s,thenφ ∈s.This follows immediately from axiom ⊞T. □

Now define K4⊞=K⊞+⊞4,where ⊞4 denotes

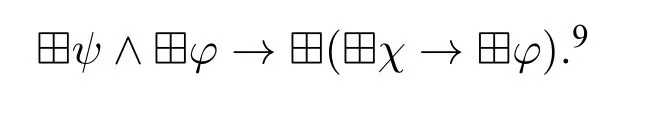
9On[17,p.220],a simpler axiom,called 40,is given as follows:⊞φ→⊞(⊞⊤→⊞φ).However,as will be explained below,our axiom ⊞4 is obtained from axiom 4 in normal modal logic via the schema(⋆).It is easy to see that 40is derivable from ⊞4 by lettingψandχbe,respectively,φand⊤.

Note that ⊞4 is also inspired by the schema(⋆).Recall that(⋆)says that given some proposition ⊞ψ,all□φcan be replaced with ⊞φ.In this way,we obtain the axiom ⊞4 from axiom 4(□φ→□□φ).In detail,

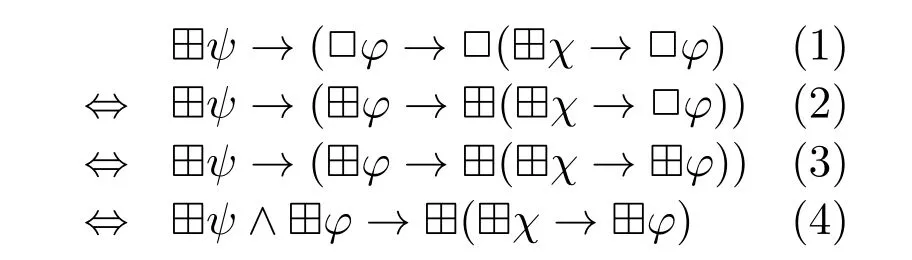
Instead of writing□φ→□□φ,we write ⊞ψ→(□φ→□(⊞χ→□φ),because under the condition that ⊞ψfor someψ,□is definable(in the current setting,“definable”means“replacable”)with ⊞.The above transitions between(1)and(2)and between(2)and(3)follow from Prop.2,and the transition from(3)to(4)is obtained via propositional reasoning.

Theorem 4.K4⊞is sound and strongly complete with respect to the class of transitive frames.

Proof.For soundness,it suffices to show the validity of ⊞4.For this,suppose,for a contradiction,that there is a modelM=〈S,R,V〉ands ∈Ssuch thatM,s⊨⊞ψandM,s⊨⊞φ,butM,s⊭⊞(⊞χ→⊞φ).ByM,s⊭⊞(⊞χ→⊞φ),we haveeither(i) there existsusuch thatsRuandM,u⊭⊞χ→⊞φ,or(ii) for allx,ifsRx,thenM,x⊭⊞χ→⊞φ.We consider the two cases:

· Case(i).ByM,u⊭⊞χ→⊞φ,we haveM,u⊨⊞χandM,u⊭⊞φ.From the latter we have two subcases:either(i1) there existsvsuch thatuRvandM,v⊭φ,or(i2)for ally,ifuRy,thenM,y⊭φ.If(i1)is the case,then bysRu,uRvand the transitivity ofR,we derive thatsRv,and thusM,v⊨φdue to the supposition thatM,s⊨⊞φ:a contradiction.If(i2)is the case,then fromM,u⊨⊞χ,it follows thatuhas a successoru′,and thusM,u′⊭φ.Similar to the first subcase,we can also arrive at a contradiction.

· Case(ii).SinceM,s⊨⊞ψ,it follows that there existstsuch thatsRt,and thusM,t⊭⊞χ→⊞φ.Then similar to case(i),we can reach a contradiction,as desired.

For completeness,suppose thats,t,u ∈Scsuch thatsRctandtRcu.BysRct,it follows that there existsψsuch that(a)⊞ψ ∈sand(b)for allφ,if ⊞φ ∈s,thenφ ∈t.BytRcu,it follows that there existsχsuch that(a′)⊞χ ∈t,and(b′)for allφ′,if ⊞φ′ ∈t,thenφ′ ∈u.To prove thatsRcu,assume that ⊞φ ∈s,it suffices to show thatφ ∈u.

From(a)and the assumption and axiom ⊞4,we obtain that ⊞(⊞χ→⊞φ)∈s.Then using(b),we derive that ⊞χ→⊞φ ∈t.This together with(a′)implies that⊞φ ∈t.Now using(b′),we conclude thatφ ∈u,as desired. □

5 Some Thoughts on Related Work

Inspired by neighborhood semantics of regular logics,in [17],a relational semantics ofL(⊞)is proposed as follows.10For the sake of comparsion,we here use ⊞to replace the symbol □adopted in[17].The change of symbol is inessential to the results below.A tupleM=〈S,N,R,V〉is said to be anon-standard model,if〈S,R,V〉is a(standard)model defined as before,andN ⊆Sis a set ofnormal worlds.11In his definition of relational frames,rather than using N,Segerberg uses Q to denote the set of singular elements,and the elements not in Q(that is,the elements in SQ,where S is the domain of the relational frame)are called normal,see[17,p.23].It should be easily seen from this and(iv′)therein that SQ is just our N.It is also worth noting that the notion of“relational frames”is called“model structures”by Lemmon on page 56 in[13].L(⊞) is interpreted on non-standard models where the cases for Boolean formulas are as usual and

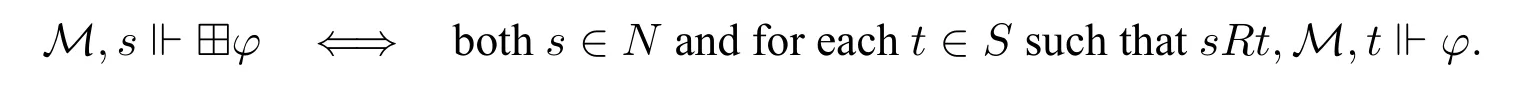
It is shown in [17,p.221] (and also [13,p.62,Corollary]) that K⊞(called D2 or CD there)is determined by the class of all non-standard frames satisfying the condition that every normal world is serial;in symbol,ifs ∈N,thensRtfor somet.Lemmon[13,p.58]calls such frames “deontic model structures”.To be consistent with our context,we will use the term“deontic non-standard frames”instead,and call those models underlying such frames“deontic non-standard models”.

Now that we have two different semantics for ⊞,one equipped with a setNof normal worlds(namely ⊩),and the other not using such worlds but changing the truth condition so that ⊞has the conjunctive requirement“all accessible worlds verifyφand some accessible world verifiesφ”for the truth of ⊞φat a world(namely ⊨),which comes to give the same logic.Although Bezerra and Venturi mention this in[1],they do not attempt to explain why it should be so.In what follows,we give an explanation of it:the latter semantics is equivalent to the special case of the former in which the normal elements are precisely those with successors.12That only normal points have successors is a condition that can be imposed on the current models without affecting the logic.(Those meeting this condition are the refined models of Lemmon([14]).)The work done in validating ⊞D is done by the converse:that all normal points have successors.

Proposition 5.For each(standard)model M and each world s in M,there exists a denotic non-standard model M′and a world s′in M′such that for all φ ∈L(⊞),we have

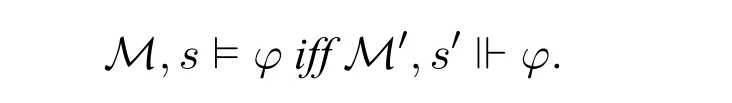
Proof.LetM=〈S,R,V〉be a (standard) model.DefineM′=〈S,N,R,V〉such thatN={s ∈S | sRtfor somet ∈S},and lets′=s.It is straightforward to see thatM′is a deontic non-standard model.We proceed by induction onφ.The nontrivial case is ⊞φ.We have the following equivalences:

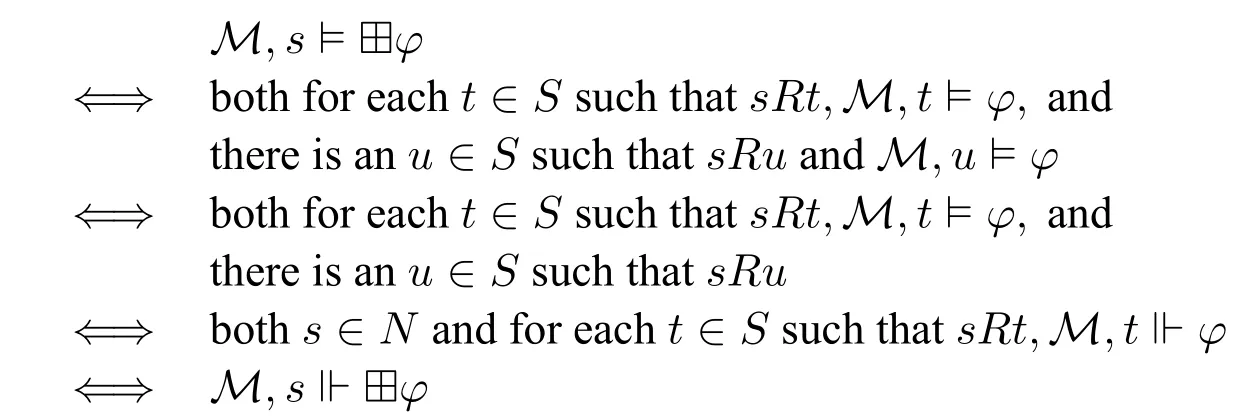
where the penultimate equivalence is due to the definition ofNand induction hypothesis. □

With Prop.5 in hand,we can give an alternative proof of K⊞with respect to the class of deontic non-standard frames.

Theorem 5.K⊞is sound and strongly complete with respect to the class of deontic non-standard frames.

Proof.The soundness is straightforward.For the completeness,by Thm.1,every K⊞-consistent set is satisfiable in a (standard) model.Then by Prop.5,every K⊞-consistent set is satisfiable in a deontic non-standard model. □

6 Discussion and Conclusion

In this paper,we built a bridge between von Wright’s deontic logic ([20]) and Bezerra and Venturi’s ⊞-logic([1]).On one hand,we provided the exact semantics for von Wright’s deontic modalities;on the other hand,we provided a suitable interpretation of ⊞-operator.Moreover,with the help of a schema,we gave an explanation of why the canonical relation in[1]is defined in that way.We also presented various axiomatizations of ⊞-logic,among which the transitive system is also inspired by the schema in question.Last but not least,we explained why the two different semantics for ⊞involved in the literature give the same logic and gave an alternative proof of completeness of a system given in[17].

For the future work,one may study a notion ofdeontic non-contingency(or its dual,deontic contingency) and its logical properties.As known,(modal) noncontingency and contingency,usually denoted by Δ and∇respectively,are defined in terms of (modal) necessity and possibility,as Δφ=：□φ ∨□¬φand∇φ=：◇φ∧◇¬φ.(See e.g.,[15,3,9,11,21,7,8,6,5])Also,we have now a notion of deontic necessity.Then it is natural to introduce notions of deontic non-contingency and deontic contingency,as the following definitions show:

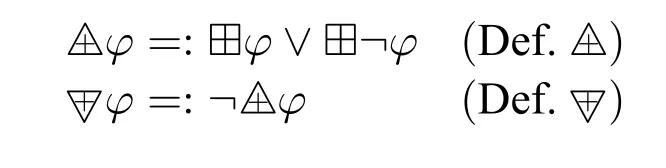
whereare read“it is deontically non-contingent thatφ”and“it is deontically contingent thatφ”,respectively.13Von Wright himself,in the original paper([20,p.4])writes“The difference between the permitted and the indifferent among the deontic modes is analogous to the difference between the possible and the contingent among the alethic modes.” So he thinks of the deontic analogue of contingency (∇φ)as simply the following:it is permissible that φ and it is permissible that not-φ,making the analogue of noncontingency be simply:it is obligatory that φ or it is obligatory that not-φ,without any further conjunct.However,as we argue before,von Wright’s obligation operator should be understood as our⊞,thus correspondingly,his deontic analogue of contingency should be understood as our notion of deontic contingency.

According to this definition and the semantics of ⊞,we can define the semantics of△+in the following:given a modelM=〈W,R,V〉,

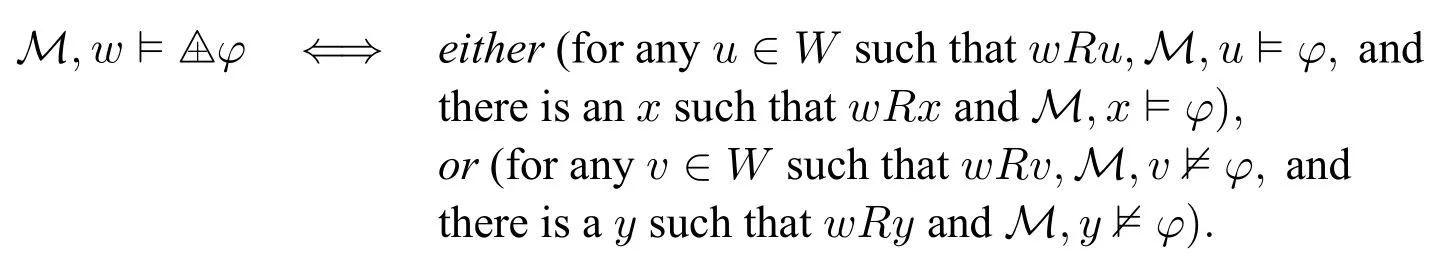
One may easily verify that ⊨△+φ↔(Δφ∧◇⊤).That is,

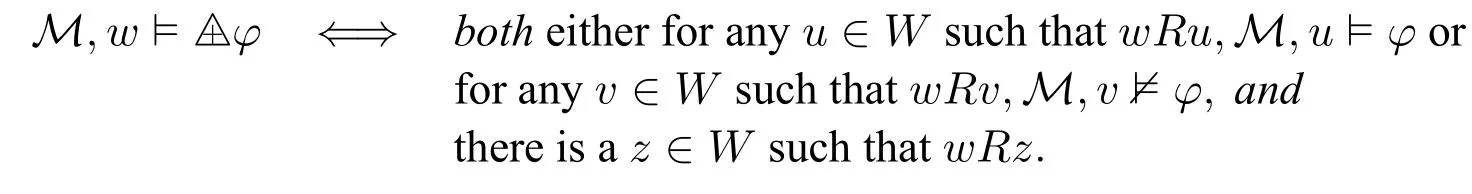
Thus on the class of serial models,△+φand Δφare equivalent,thus△+and Δ are interdefinable.This is similar to the case for ⊞and□:firstly,⊨⊞φ↔(□φ∧◇⊤);secondly,on the class of serial models,⊞φand□φare equivalent.

Different from the case for ⊞and□,△+and Δ arenotinterdefinable over the class of all models.For instance,consider the following two simple models:

It should be straightforward to show that(M,s)and(M′,s′)cannot be distinguished by anyL(Δ)-formula.However,M,s⊭△+φandM′,s′⊨△+φfor allφ ∈L(△+).

One may easily verify that the following formulas are valid.This is similar to the case in non-contingency except for the inference rule wGEN△+,refer to e.g.[11].

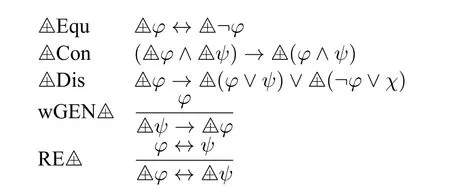
Note that we have noas a validity,or equivalently,the ruleis not validity-preserving.This is an important distinction betweenand Δ.Also,note that the rule wGENis equivalent to a formula14It may be interesting to see that unlike in the case of the almost definability schema(⋆),the formula ψ in wGEN△+cannot be replaced with ⊤.

We have the following almost-definability schemas.

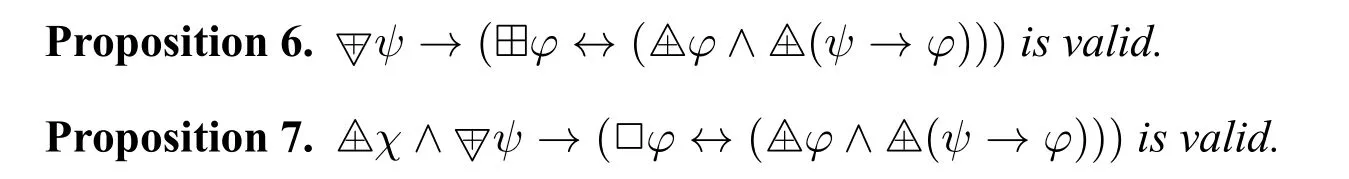
In the current stage,we do not know whether the above validities(plus TAUT and MP)completely axiomatize the△+-logic over the class of all frames.The difficulty lies in the requirement that the evaluated point should be serial in the semantics.We will leave it for future work.