基于Gaussian-Hermite矩的旋转运动模糊不变量

郭锐，贾丽，郝宏翔，墨瀚林，李华

1. 中国科学院计算技术研究所智能信息处理重点实验室，北京 100190；2. 中国科学院大学，北京 100049； 3. 91977部队，北京 100036

0 引 言

如何正确识别图像中的目标是计算机视觉和模式识别领域的经典问题。基于各种图像特征的方法已被多数研究者接受。在相机成像曝光过程中，由于大气干扰、相机失焦以及相机与场景相对运动等环境和现实很多因素会造成图像的退化，因此，理想的图像特征应当对这些变化具有不变性。图像运动模糊是在相机成像的过程中由于相对较长的曝光时间及相机与场景相对运动导致的，可视做一定时间区间内对图像密度函数的积分。按照曝光时间内相机相对于场景在3维空间的运动形式，图像的运动模糊可分为直线运动模糊、旋转运动模糊、径向运动模糊以及其他由上述3种模糊多个叠加形成的复杂运动模糊。例如，安装在高速旋转的导弹或机械的相机拍摄的图像会产生旋转运动模糊。

本文以旋转运动模糊的退化模型为出发点，提出了旋转运动模糊Gaussian-Hermite(GH)矩，并对已有的几何矩旋转变换不变量向GH矩不变量进行拓展和筛选，构造了一组由5个对旋转变换和旋转运动模糊保持不变的GH矩旋转运动模糊不变量组成的特征向量(rotational motion blur Gaussian-Hermite moment invariants RMB_GHMI-5)，该组特征向量可从受到严重噪声干扰的旋转变换叠加旋转运动模糊的图像中直接进行图像检索，而无需前置复杂的“去模糊”预处理过程，从而实现了很好的识别效能。

1 相关工作

在运动模糊图像模式识别方面，大多数工作选择去模糊策略，达到尽可能好的效果后再进行下一级处理。在去模糊领域，按照使用的方法类型可分为基于自然场景统计的方法和基于机器学习的方法。基于自然场景统计的方法主要有：Whyte等人(2012)针对相机绕光轴旋转产生的模糊，提出基于简单投影变换模型的非统一模糊图像复原，对模糊图像建立了描述曝光时间内相机的旋转速度的参数。Zheng等人(2013)研究相机的径向运动模糊，但在模糊核估计时需要手动选择。Wang等人(2017)通过使用Radon 变换求模糊方向和双频谱建模来找出直线运动模糊的长度，该算法是基于空间和频域分析的结合。Sun等人(2018)对于受到高斯噪声影响的图像盲恢复提出重加权ADMM(alternating direction method of multipliers)算法，但由于在非凸的ADMM 中，拉格朗日乘子取值很大，使得算法迭代较慢。Sun等人(2019)提出了一种基于参数预热技术的交替极小化算法。基于机器学习的方法主要有：Zhou等人(1988)率先将HNN(Hopfield neural network)应用到图像复原领域。Tao等人(2018)基于卷积神经网络提出一种深度学习方法用于图像去运动模糊。Kupyn等人(2019)进一步改进网络，将特征金字塔网络作为DeblurGAN-v2的核心构建块，与各种骨干网络配合使用，在性能和效率之间更加均衡。Liang等人(2019)利用头脑风暴优化算法自动搜寻BP(back propagation)神经网络更佳的初始权值和阈值，提升了网络性能。Qiu和Zhang(2020)基于cGANs(conditional generative adversarial nets)生成了端到端的去旋转运动模糊的网络。许多去模糊的研究工作在指定任务中取得了很好效果，但在图像处理和识别领域一直面临着“不适定”(Flusser和Suk，1998)或“非必要”的挑战。首先，无论采用何种方法对图像进行复原都是不稳定且耗时的，恢复工作难以完美实现。其次，在目标识别和语义理解等无需人类视觉系统参与处理的场景，对模糊图像进行恢复经常是非必要的。

如果免去图像恢复的预处理过程，直接提取具有运动模糊不变性的图像特征，就会使图像识别效率加速。因此，构造运动模糊图像的不变特征成为图像识别领域的一个重要研究方向。Suk和Flusser(1996)基于中心对称卷积核构造了直线运动模糊矩不变量。Flusser和Suk(1998)提出模糊几何矩不变量。Flusser和Zitov(1999)提出了同时对模糊变换和相似变换有不变性的复数矩不变量。Zhang和Tan(2002)提出了仿射—卷积混合不变量。Zitov和Flusser(2003)提出使用模糊不变量替换已有仿射矩不变量中的中心矩的方法构造仿射—卷积混合不变量的显式表达式。Ojansivu和Heikkilä(2008)基于中心对称卷积核在频域内对相位谱没有影响，提出局部相位量化特征描述子。这种假设使研究工作取得一定进展，但不适用于实际中复杂运动形式的模糊图像的识别。Zhang等人(2010)基于正交 Legendre 矩进行了改进。Flusser等人(2015)基于几何矩提出了7阶以内的直线运动模糊不变量，并给出了构造方法，在与去模糊方法的图像识别对比实验中，显示出更好性能。

关于旋转运动模糊的研究，一般思路是根据运动轨迹为一系列同心圆的性质，将模糊图像从笛卡儿坐标系转换到极坐标系，看成直线运动模糊来处理(Morimoto等，2011)。但这种研究思路的本质仍然是去模糊，不但没有解决本质问题，坐标系的转换还会引入新的噪声，对后续的识别和分析产生影响。Hao等人(2021)基于旋转运动模糊退化模型以及几何矩，得到7个旋转运动模糊几何矩不变量RMBMI-7(rotational motion blur moment invariants)，并在实验中证实了其对于旋转运动模糊具有良好的不变性和区分性。但是由于几何矩本身抗噪性能较差，因此在实际应用中，适用性受到制约。除上述工作之外，对于旋转运动模糊图像不变特征的有价值研究较为鲜见。

2 理论基础

2.1 旋转运动模糊的退化模型

当被摄物体与感光元件之间存在相对运动时，在一次快门时间内，光在成像平面上的会产生非正常累积，造成存在运动模糊的图像。在感光元件与被摄物体存在轴向旋转运动的情况下，模糊路径可视为以相机与被摄物体为轴心、一系列以轴心为圆心的同心圆。由于快门时间通常较短，且变速旋转运动可分解成多个匀速旋转运动，因此本文着重研究旋转中心已知并以其为原点构建坐标系且角速度为常数的匀速旋转运动模糊，其连续退化模型(Gonzales和Wintz，1987)为

(1)

式中，g(x(g),y(g)) 为模糊图像，T为曝光时间，f(x(t),y(t))为原图像的某像素点在经过t时间旋转变换后的终点坐标，而旋转角度是关于时间t的函数，设为φ(t)=ωt。因为旋转运动模糊的形成过程中，原图像只绕旋转中心发生旋转变换，因此原图像的坐标系与模糊图像的坐标系之间也构成了旋转变换关系，旋转角度是常数，记做α(正负两个方向)。根据上述关系可得

(2)

(3)

结合式(2)和式(3)，可得(x(t),y(t))与旋转路径落点坐标(x(g),y(g))的关系，具体为

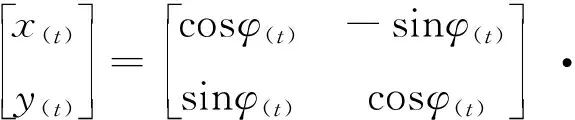
(4)

设θ(t)=φ(t)-α=ωt-α，可得

(5)

旋转运动模糊的离散退化模型为

(6)

2.2 GH矩

根据正交多项式理论，Teague (1980)提出Zernike 矩和Legendre 矩，将正交矩引入图像不变特征分析领域，解决了几何矩不变量天然存在的信息冗余问题。Yang等人(2011)证明了GH矩旋转不变量与几何矩旋转不变量具有相同的形式，所有已经发现的几何矩旋转不变量都可以用于构建GH矩旋转不变量，并给出了构建方法，但未考虑旋转运动模糊的场景。本节在介绍GH矩之前，先介绍GH多项式。

在连续区间(∞,-∞)上，第n阶的Hermite多项式的定义为

Hn(x)=(-1)nex2(dn/dxn)e-x2

(7)

Hermite多项式的递推公式为

Hn+1(x)=2xHn(x)-2nHn-1(x),n≥1

(8)

式中，初始条件为H0(x)=1，H1(x)=2x。加入权函数w(x)=e-x2, Hermite多项式满足正交性，即

(9)

式中，Hm(x)和Hn(x)分别为m阶和n阶Hermite多项式函数，δmn为克罗内克符号，当m=n时，δmn= 1，反之为0。此时Hermite多项式是正交的，但不具有归一性。正交且归一的Hermite多项式的形式为

(10)

此时加入控制衰减的自定义尺度因子σ，更通用的正交且归一的GH多项式定义为

(11)

以GH多项式为基函数，在(m,n)阶下的GH矩的定义为

(12)

式中，f(x,y)为图像的强度函数。

3 基于GH矩的旋转运动模糊不变量

基于旋转运动模糊退化模型，该类图像的形成是对原图像进行一系列旋转变换后的结果的叠加均值。本节围绕旋转GH矩不变量能否在旋转运动模糊中保持不变性展开讨论：首先给出旋转运动模糊图像GH矩的定义，再将该GH矩带入旋转矩不变量中，筛选出具有稳定的不变性的旋转变换和旋转运动模糊的GH矩不变量，即旋转运动模糊GH矩不变量(RMB_GHMI)，构成一组特征向量应用于图像检索和目标识别等领域。

3.1 模糊图像的GH矩

结合旋转运动模糊的退化模型和GH矩的定义，模糊图像g(x(g),y(g))的GH矩为

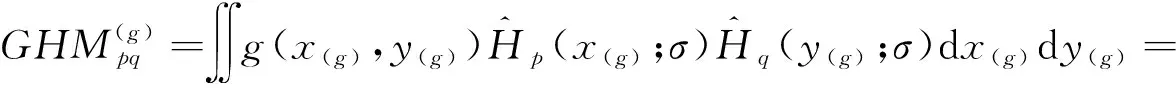
(13)

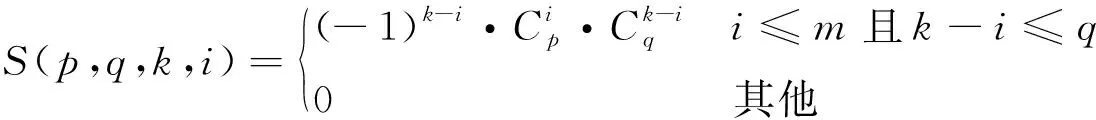
下面，对式(13)中的推导过程做几点说明：

1)根据式(5)可得

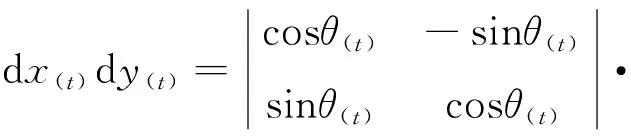
(14)

然后将式(5)和式(14)代入。

2)将双重积分中被积函数的两部分分别展开为多项式，式中i≤p,j≤q。

3)将被积函数去括号，然后按照x(t)和y(t)的阶数进行合并。

4)由式(12)中的定义，引入GH矩。

5)由于推导过程中说明3)的合并使两个组合数发生了变换，说明2)中i≤p,j≤q的约束不再有效，因此为保证推导的正确性和严谨性，将结果中的组合数用新的函数改写，并指明当套用结果代入各参数时一旦违反新组合数i≤p,k-i≤q的约束时，此项不符合实际意义，系数为0。

6)由说明5)可看出旋转运动模糊图像的GH矩是由原图像GH矩的线性组合构成，定义H(p,q,k)为各项系数。旋转运动模糊GH矩不变量的构建过程就是消除各项系数的过程。

离散情况下旋转运动模糊图像的GH矩为

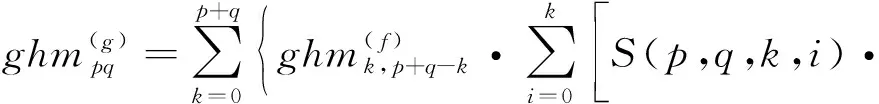
(15)

3.2 旋转运动模糊图像的GH矩不变量

式(13)给出了模糊图像GH矩与原图像GH矩的关系式，构建旋转运动模糊矩不变量的关键就是寻找各项系数之间的关系，以消去各项矩中的时间参数和正弦余弦函数。

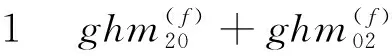
证明：由式(13)可得

(16)

根据式(16)可得系数之间的关系，即

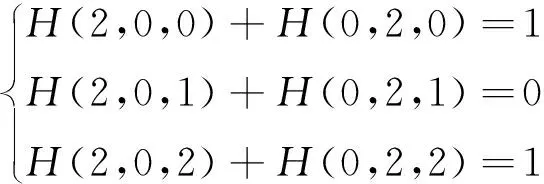
(17)

因此

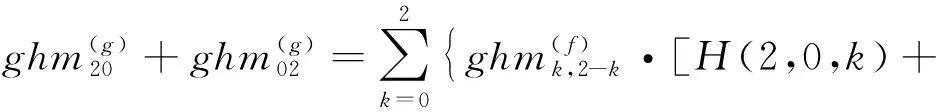
(18)

由于旋转运动模糊GH矩不变量的项数较多且系数复杂，人工推导效率极低，因此本文不直接构建不变量，而是通过编写Maple程序将判断旋转运动模糊不变性的过程封装起来，以不变量为参数。具体步骤为：1)将不变量中的模糊矩按式(13)展开为原矩的线性组合；2)合并同项系数；3)简化系数,以消去各项矩中的时间参数和正弦余弦函数为主；4)判断简化后的各项原矩是否仍能构成不变量。待测不变量为Mo和Li(2021)方法中的旋转矩不变量经Yang等人(2011)的方法扩展到GH 矩的旋转GH矩不变量。

3.3 RMB_GHMI-5

基于上述算法，本文得到一系列具有旋转变换和旋转运动模糊不变性的GH矩不变量。为了获得一组稳定的旋转运动模糊GH矩不变量，对同一幅图像做不同程度的旋转运动模糊，合成了10幅测试图像，分别计算待测不变量的值，并求得其平均相对误差。具体为

(19)

经过对多组图像进行上述相同实验后，筛选出平均相对误差最小的5个不变量，组成具有相当稳定性的旋转运动模糊特征向量，记做RMB_GHMI-5。这5个不变量的具体计算为

RMB_GHMI(1)=ghm20+ghm02
RMB_GHMI(2)=ghm40+2ghm22+ghm04

RMB_GHMI(3)=

RMB_GHMI(4)=

RMB_GHMI(5)=

(20)

4 实验与分析

为了测试RMB_GHMI-5的不变性和图像检索性能，以MATLAB为实验平台进行实验与分析，运行平台为CPU频率2.80 GHz、内存16 GB的计算机。

4.1 不变性测试

(21)

式中，X表示清晰图像，Y表示模糊后的图像，xi为原图像的RMB_GHMI-5各分量的数值，yi为模糊图像的RMB_GHMI-5各分量的数值，n为RMB_GHMI-5的特征维数。

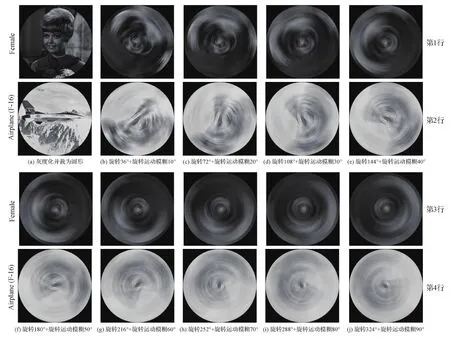
图1 原始图像和变换/退化处理后的合成图像Fig.1 Demonstration of original images and transformed/degraded composite images((a)grayscale and crop to circle;(b)rotate 36°+rotational motion blur 10°；(c)rotate 72°+rotational motion blur 20°；(d)rotate 108°+rotational motion blur 30°；(e)rotate 144°+rotational motion blur 40°；(f)rotate 180°+rotational motion blur 50°；(g)rotate 216°+rotational motion blur 60°；(h)rotate 252°+rotational motion blur 70°；(i)rotate 288°+rotational motion blur 80°；(j)rotate 324°+rotational motion blur 90°)

表1和表2分别是Female和Airplane(F-16)经图1处理后RMB_GHMI-5各分量的值以及特征距离。可以看出，即使在旋转运动模糊程度极大，人眼完全不可辨认时，本文给出的RMB_GHMI-5依然能保持很小的修正卡方距离，表明RMB_GHMI-5在旋转变换和旋转运动模糊叠加的情况下具有良好的稳定性和不变性。

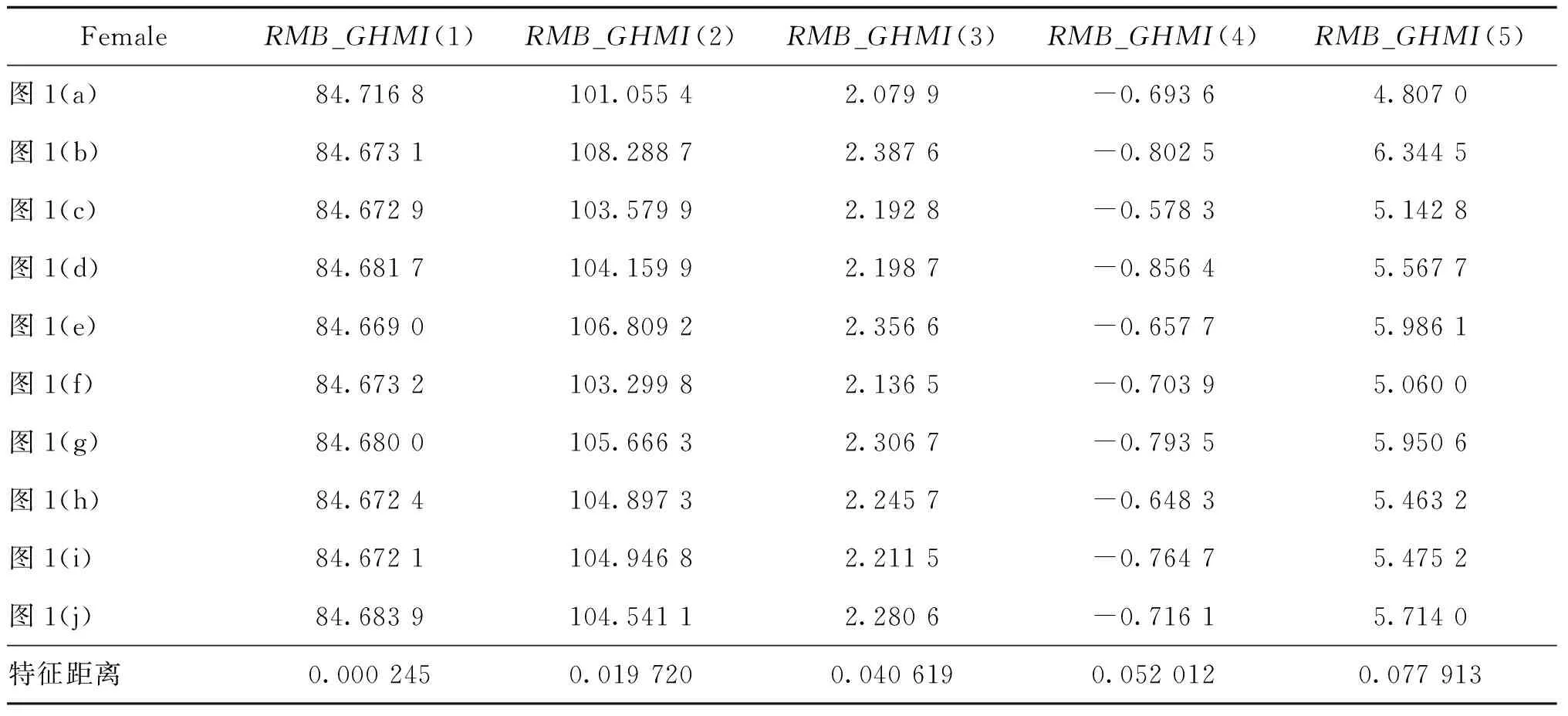
表1 Female经处理后RMB_GHMI-5的值Table 1 The values of RMB_GHMI-5 for Female after transforming

表2 Airplane (F-16)经处理后RMB_GHMI-5的值Table 2 The values of RMB_GHMI-5 for Airplane (F-16) after transforming

4.2 图像检索实验

另外，本文尝试挑战在对称图像中的检索性能。对称图像相比于一般图像，对算法的区分性要求更高。在Butterfly Image数据集(Li等，2019)中随机挑选30幅相似的蝴蝶图像作为数据集B，然后按数据集A的方式，构成测试数据集B_G、B_SP、B_P和B_S，每个数据集有300幅图像。

选取4个同类方法与本文方法进行对比，分别是：Hu(1962)提出的7个几何矩不变量、Yang等人(2011)提出的7个GH矩旋转变换不变量、Hao等人(2021)提出的7个几何矩旋转模糊不变量、Yang等人(2011)与Hu(1962)组成的12维几何矩—GH矩混合特征向量。同时，将RMB_ GMHI-5与Hao等人(2021)提出的7个几何矩旋转模糊不变量组合起来形成的12维GH矩与几何矩融合的特征向量参与对比实验。实验使用特征向量间修正的卡方距离作为衡量图像相似度的依据，用P-R(precision-recall)曲线作为观察图像检索实验结果的工具，对比测试RMB_GHMI-5的性能。

图2和图3分别展示了数据集A和数据集B中的一部分。图4—图11分别展示了在旋转变换和旋转运动模糊后，添加高斯噪声、椒盐噪声、泊松噪声和乘性噪声的测试数据集A_G、A_SP、A_P、A_S和B_G、B_SP、B_P、B_S的一部分。

图2 数据集A部分示例Fig.2 Examples of dataset A

图3 数据集B部分示例Fig.3 Examples of dataset B

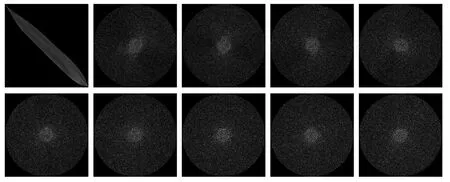
图4 添加高斯噪声的测试数据集A_G示例Fig.4 Examples of test dataset A_G with Gaussian noise added

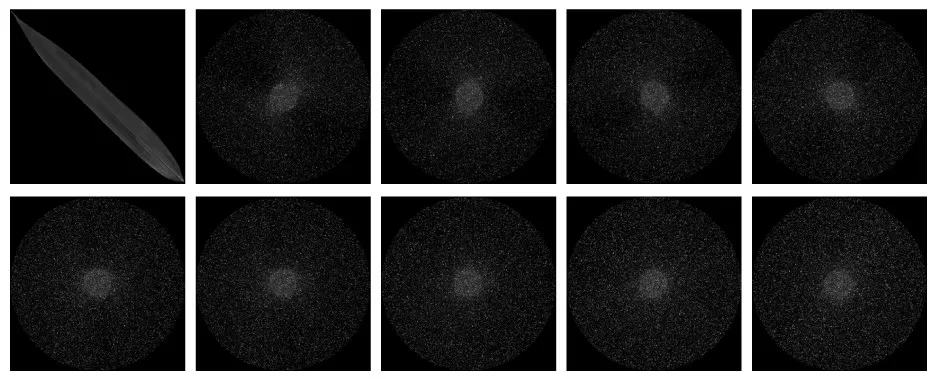
图5 添加椒盐噪声的测试数据集A_SP示例Fig.5 Examples of test dataset A_SP with salt and pepper noise added

图6 添加泊松噪声的测试数据集A_P示例Fig.6 Examples of test dataset A_P with Poisson noise added

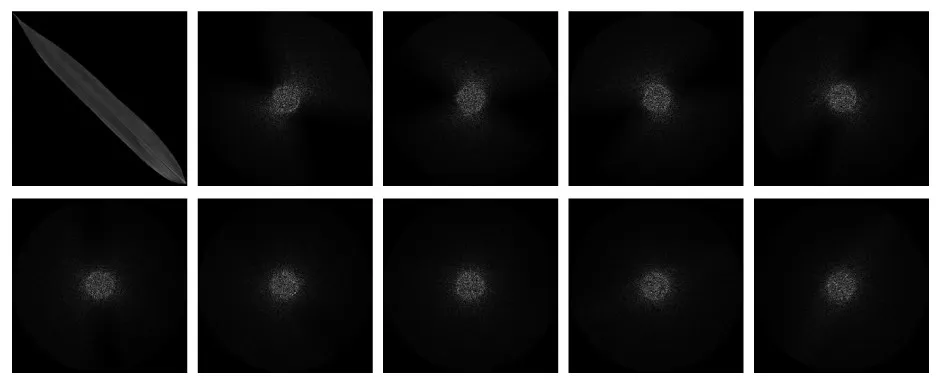
图7 添加乘性噪声的测试数据集A_S示例Fig.7 Examples of test dataset A_S with speckle noise added

图8 添加高斯噪声的测试数据集B_G示例Fig.8 Examples of test dataset B_G with Gaussian noise added

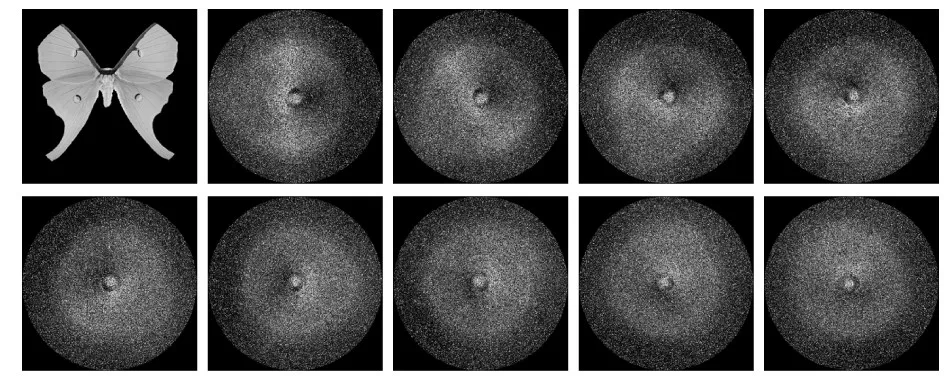
图9 添加椒盐噪声的测试数据集B_SP示例Fig.9 Examples of test dataset B_SP with salt and pepper noise added

图10 添加泊松噪声的测试数据集B_P示例Fig.10 Examples of test dataset B_P with Poisson noise added

图11 添加乘性噪声的测试数据集B_S示例Fig.11 Examples of test dataset B_S with speckle noise added

4.3 实验结果分析

图12展示了不同测试数据集图像检索实验的P-R曲线。从图12(a)—(d)可以看出，RMB_GHMI-5在树叶图像极严重的模糊和噪声干扰下，图像检索方面的性能远超Hu (1962)提出的7个几何矩不变量、Yang等人(2011)提出的7个GH矩旋转变换不变量和Hao等人(2021)提出的7个几何矩旋转运动模糊不变量。另外，12维GH矩与几何矩融合的特征向量检索准确度最高，这主要得益于特征向量维数的增加。从图12(e)—(h)可以看出，RMB_GHMI-5在更复杂的对称图像中的表现也优于其他对比方法。在蝴蝶图像受到极严重的模糊和噪声干扰下，图像检索方面的性能明显优于同类其他更高维特征向量。

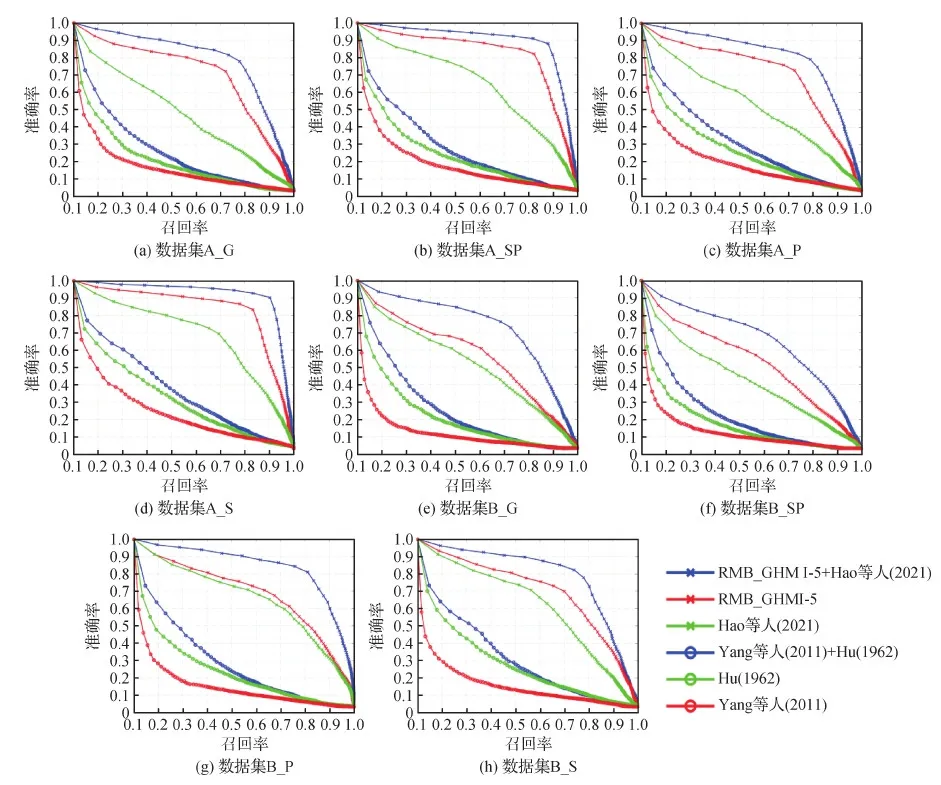
图12 不同数据集图像检索实验P-R曲线Fig.12 P-R curves of image retrieval experiments on different datasets((a)dataset A_G；(b)dataset A_SP；(c)dataset A_P；(d)dataset A_S；(e)dataset B_G；(f)dataset B_SP；(g)dataset B_P；(h)dataset B_S)

实验选取了两种数据集，分别仿真其受到旋转、旋转运动模糊以及4种常见的图像噪声干扰，实验结果如表3所示。可以看出，在80%召回率下，本文方法相较在不同数据集、不同噪声干扰下对应同类性能最好的Hao等人(2021)方法，在Flavia数据集，在高斯噪声、椒盐噪声、泊松噪声和乘性噪声干扰下，准确率分别提高了25.89%、39.95%、22.79%和35.80%；在Butterfly Image数据集，在高斯噪声、椒盐噪声、泊松噪声和乘性噪声干扰下，准确率分别提高了4.79%、7.63%、5.65%和18.31%。RMB_GHMI-5的检索准确率有显著提升。

表3 RMB_GHMI-5与Hao等人(2021)在80%召回率下准确率提升结果Table 3 The result of precision rates improve by RMB_GHMI-5 comparing with Hao et al.(2021)at 80% recall rate /%

由此可见，RMB_GHMI-5在严重的旋转运动模糊和噪声干扰情况下，该特征向量的区分性较早前方法有了明显改善，证明了本文方法在存在强干扰情况的真实场景中，对旋转运动模糊的图像检索、识别任务更具优异性能和应用潜力。

5 结 论

基于旋转运动模糊退化模型与GH矩理论，本文提出了对旋转变换和旋转运动模糊保持不变的旋转运动模糊GH矩不变量，并构建了一个5维旋转运动模糊不变特征向量RMB_GHMI-5。

经过实验测试和对比，该特征向量对旋转变换和旋转运动模糊都具有很好的不变性和区分性，在噪声相当严重的情况下，仍能保持良好的检索和识别性能，且相比已有同类方法，图像检测准确率有了显著提升。当模糊增大至人眼无法辨别程度，图像内容发生巨大改变。甚至模糊程度在通用的神经网络都无法对网络进行训练的情况下，RMB_GHMI-5依然保持了很好性能。因此在图像检索和模式识别领域，基于手工特征的不变量研究具有非常重要价值。

本文工作还值得继续推进。如何将已经得到的不变特征与神经网络相结合，改进网络结构，实现更具实用性的算法突破，将是未来一段时间的研究方向。