高性能整数倍稀疏网络行为识别研究

臧影，刘天娇，赵曙光*，杨东升

1. 中国科学院大学计算机科学与技术学院, 北京 100049； 2. 中国科学院沈阳计算技术研究所，沈阳 110168；3. 湖州师范学院信息工程学院，湖州 313000； 4. 烟台创迹软件有限公司，烟台 264000

0 引 言

人体行为识别已经在视频监控、人机交互、无人驾驶及虚拟现实中得到了广泛应用(Carreira和Zisserman，2017；Martinez-Hernandez等，2018；Wang和Wang，2017)。最初行为识别算法使用RGB图像序列(Zhu等，2018；Sun等，2018)、深度图像序列(Xu等，2017；Baek等，2017)或这些数据的融合(Feichtenhofer等，2016；Wang等，2016)。由于视频序列数据量非常庞大，对于行为识别任务来说，存在大量信息冗余。如图1所示，人体骨架数据具有轻量级及抗干扰性强等优点，仅包含人体关节点位置坐标信息，提供了高度抽象的信息，不受外界环境变化影响。骨架数据还可通过Openpose人体姿态估计算法(Cao等，2021)及Microsoft Kinect传感器(Zhang等，2012)轻松获得，所以基于骨骼的行为识别吸引了越来越多研究者的关注。

图1 NTU RGB+D数据集中RGB图像序列与骨架序列Fig.1 RGB image sequence and skeleton sequence in NTU RGB+D dataset

基于卷积神经网络(convolutional neural networks，CNN)的行为识别算法通常专注于图像任务，而时间信息是行为识别性能提高的关键因素。如何在CNN中充分地利用空间和时间信息是行为识别的关键问题。Li等人(2018)提出了一种端到端的共现特征学习框架，使用CNN自动从骨架序列中学习分层的共现特征。在该框架中逐步汇总不同层级的上下文信息，在时域和空域将它们组合成语义表示，并总结出一个简单而又非常实用的方法来调节按需聚集的程度。Li等人(2019)为了更高效地表示骨架，对骨架信息进行编码，采用多流CNN模型对骨架数据进行识别。Caetano等人(2019a)引入一种新的骨架图像表示，作为CNN的输入，称为Skele-Motion。提出的方法通过显式计算骨架关节大小和方向值编码时间动态信息，采用不同时间尺度计算运动值，以将更多的时间动态信息聚集到表示中，从而使其能够捕获动作中涉及的远程关节交互以及过滤嘈杂的运动值。Caetano等人(2019b)对Skele-Motion进一步进行改进，引入树结构参考关节图像(tree structure reference joint image，TSRJI)作为一种新颖的骨架图像表示。

循环神经网络(rerrent neural network，RNN)(Zhang等，2018)是一种处理序列数据的有效方法，但是RNN结构缺乏空间建模能力，为了解决该问题，Wang和Wang(2017)提出一种新颖的双流RNN架构，对基于骨架的动作识别的时间动态和空间配置进行建模。针对时间流提出两种不同结构：堆叠RNN和分层RNN，其中分层RNN是根据人体运动学设计的。文章提出两种有效方法，通过将空间图转换成关节序列对空间结构进行建模，为了提高模型的通用性，进一步利用基于3D变换的数据增强技术，在训练过程中变换骨架的3D坐标。该方法为各种动作(即通用动作，互动活动和手势)带来了显著的改进。Xie等人(2018)提出一种端到端的内存注意网络(memory attention networks， mANs)，该网络由一个时间注意力校准模块(time attention calibration module，TACM)和一个时空卷积模块(spatio-temporal convolution module，STCM)组成。并利用CNN进一步建模骨骼数据的时空信息。这两个模块(TACM和STCM)无缝地形成了可以以端到端的方式进行训练的单个网络体系结构。Zheng等人(2019)提出了注意力递归关系长短时记忆网络(attention recurrent relational network long-short term memory，ARRN-LSTM)，同时对骨架中的空间和时间信息建模以进行动作识别。嵌入在单个骨架中的空间模式是通过递归关系网络学习的，然后使用多层LSTM-提取骨架序列中的时间特征。为了利用骨架中不同几何形状之间的互补性进行关系建模，设计了一种双流体系结构，学习关节之间的关系并同时探索流之间的潜在模式。同时，引入一种自适应注意模块用于关注针对特定动作的骨架潜在区分部分。

目前，基于骨架行为识别的大多数算法都是利用空间和时间两个维度的信息才能获得好的效果， 而GCN(graph convolutional network)能够将空间和时间信息完美地结合起来。Yan等人(2018)提出一种动态骨架的新模型，称为时空图卷积网络(spatial temporal graph convolutional networks，ST-GCN)，可以通过自动从数据中学习时空模式来超越之前方法的局限，具有更强的表达能力和泛化能力。Shi等人(2019a)提出一种新颖的两流自适应图卷积网络(two-stream adaptive graph convolutional networks，2 s-AGCN)用于基于骨骼的动作识别。BP(back propagation)算法以端到端的方式统一或单独学习模型中图的拓扑。这种数据驱动的方法增加了图构建模型的灵活性，并为适应各种数据样本带来了更多的通用性。Li等人(2019)引入称为A-link推理模块的编码器—解码器结构，直接从动作中捕获特定动作的潜在依赖关系，扩展现有骨架图以表示更高阶的依存关系，并将这两种类型的链接组合成广义骨架图，进一步提出了行动结构图卷积网络(action-structure graph convolutional network，AS-GCN)，将行动结构图卷积网络和时间卷积网络(temporal convolutional network, TCN)作为基本构建块进行堆叠，学习时空动作识别功能。

然而，之前的方法都具有较高的计算复杂度，训练过程效率低下。目前的行为识别算法大多专注于算法的性能。如何在保证精度的同时减少算法计算量是行为识别需要解决的关键性问题。Cheng等人(2020)受Shift CNNs(generalized low-precision architecture for inference of convolutional neural networks)(Jeon和Kim，2018；Wu等，2018；Zhong等，2018)的启发，成功地将shift操作与轻量级的点卷积相结合，并引入到GCN中替代常规的卷积操作，不但降低了计算量，而且将感受野扩大到全局，提高了算法性能。在3个基于骨骼动作识别的数据集上，Shift-GCN明显超出现有方法，计算复杂度降低为原来的额1/10以上。

本文对Shift-GCN进行更加深入研究，发现网络的特征矩阵及注意力参数存在冗余，通过对网络结构的合理化设计及注意力参数详细分析，提出了精度更高的网络结构IntSparse-GCN(integer sparse graph convolutional network)。

本文主要贡献如下：1)在Shift-GCN基础上，对稀疏的shift操作进行改进，为尽量均衡每个关节点的特征向量中的0，改造了原始标准的网络结构，设计输入输出通道为关键点整数倍的网络结构，有效提高了识别准确率。2)对Shift-GCN注意力函数进行分析，发现大部分参数作用在关节点上的特征后，不但没有提高识别精度反而影响精度，为此设计了基于区间的自动搜索算法，满足区间范围内的参数不需要再进行乘法操作，不但提高了精度，速度也进一步提升。得到的关节点特征具有很强的稀疏性，为下一步的剪枝及量化提供了可能性。

1 相关工作

1.1 基于骨架的GCN行为识别算法

图2 ST-GCN网络结构Fig.2 ST-GCN network structure

在ST-GCN基础上，Shi等人(2019a)提出一种自适应图卷积神经网络2 s-AGCN模型，能够在端到端网络中自适应地学习不同层和骨架样本的图拓扑结构。然而ST-GCN的注意力机制不够灵活，距离较远的关节点之间由于不存在直接连接而学习不到二者间的相关性。骨骼的长度和方向能够表达更丰富的运动信息。ST-GCN只使用骨架关节点的一阶特征，而2 s-AGCN使用骨骼的二阶特征，并与一阶信息相结合，显著提高了模型分类正确率。Shi等人(2019a)又进一步提出性能更高的MS-AAGCN(multi-stream attention enhanced adaptive graph convolutional neural network)，将注意力模块嵌入图卷积层中，帮助模型选择性地提取更具区分性的节点和通道，并通过关节和骨骼信息，在时间维度构造运动信息，使用4流合并的性能大幅提高了模型性能。

1.2 shift卷积算法

传统卷积具有较强的计算复杂度，随着卷积核的增加计算量成倍增加，导致深度神经网络扩展困难。从本质而言，2维卷积主要是在空间域对特征进行层次化提取，在通道域对层叠的特征进行整合。Wu等人(2018)提出了shift方法，将空间域的特征进行不同方向平移，使用点卷积在通道域对特征进行融合，搭建端到端训练模型，附带一个超参控制准确率与效率的权衡。可以证明shift卷积层的输出和输入是关于通道排序无关的，并且shift卷积的感受野更加灵活，只需要通过简单地改变shift距离实现。Zhong等人(2018)将shift算子引入CNN，构造了3个基于shift的高效紧致的CNN网络，在保证预测精度的同时，减少了GPU(graphics processing unit)上的推理时间，shift操作避免了内存的复制，因此具有较快速度。Cheng等人(2020)将0参数的shift操作应用到空间模块和时间模块中，提出一种更轻量级的Shift-GCN模型，大幅减少了模型的计算复杂度。与传统shift操作一样，Shift-GCN可以分为shift操作和点卷积两个阶段，然而传统shift操作主要用在标准的图像数据中，骨架数据是非规则的图拓扑结构，因此构造了一种新的空间shift方法，根据感受野不同可以分为局部shift和非局部shift的方法，非局部的shift方法具有更大的感受野，能够更好地克服人体的空间结构的限制，使每个节点都能够接收到其他节点的信息。实验证明非局部的shift方法具有更优的性能。将shift算子引入GCN，不但构造了轻量级的动作识别算法，还有效提升了模型性能。

2 提出的方法

首先引入基于通道整数倍的空间shift算法，并借鉴SparseShift-GCN的shift算法，将部分通道位置置0，使特征通道接近一半的位置为0，使其成为具有强规律性的稀疏特征矩阵，为其他研究者的模型剪枝及量化提供了可能性。然后对Shift-GCN中的mask掩膜函数进行研究分析，发现其mask掩膜函数80%以上的参数未起作用，为此本文构建了新的自适应mask掩膜函数，使速度和精度均有提升。

2.1 关节点整数倍空间shift算法

虽然Shift-GCN在很大程度上减少了算法的计算量。但是网络特征存在冗余，网络内部结构设计还没有达到最优化程度。为了进一步解决特征冗余，本文提出首先将网络每层的输入输出设置成关节点的整数倍，然后采用将奇数列向上移动、偶数列向下移动的方式对特征矩阵进行移动操作。为了防止过拟合，提升模型泛化能力，将移出部分用0代替。这样设计使网络中每个关节点的特征中的0的个数几乎一样，有效提高了模型的鲁棒性和识别精度。

图3为网络通道整数倍与非整数倍的结构对比。图中N为人体关节点的个数，C为网络某一层的输出通道数量，k为正整数，k=1,2,…,n。图中的N= 7，当网络某一层的输出通道为10时，该层中的每个特征向量的0的个数是不相等的，0的个数从上到下分别为5、4、3、3、3、3、4，这样会导致每个特征向量的值不均衡。而当C=2kN-1时(k= 1时)，即C=2×7-1，则每个特征向量中0的个数都是6，这样使每个特征向量中的0都是均衡的，能有效增加模型的稳定性。

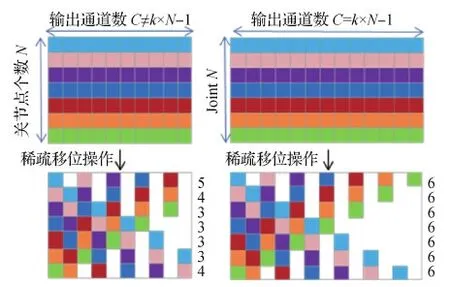
图3 网络通道整数倍与非整数倍的结构对比Fig.3 Structure comparison between integer multiples and non-integer multiples of network channels

从图3中可以看出，提取的特征矩阵是非常稀疏的，接近一半的特征值是0，这些值对识别率没有任何贡献，不需要对其进行任何计算，而这样的设计并没有降低分类精度，反而提高了精度。这样的稀疏特征矩阵为其他研究者压缩模型、加速网络提供了依据。所以专门针对整数倍的shift操作设计了高效的网络结构IntSparse-GCN。图4展示关节点为25时的IntSparse-GCN结构图，。其各层网络输入输出如表1所示。

图4 关节点为25时的IntSparse-GCN结构图Fig.4 IntSparse-GCN structure diagram when key point is 25

表1 关节点为25时的IntSparse-GCN各层网络输入输出Table 1 The input and output description of each layer of IntSparse-GCN when the node is 25

为了与Shift-GCN进行对比，基础网络依然为10层。为了保持总体参数量与Shift-GCN相当，将网络前4层输出设置为74，5—7层输出设置为124，8—10层输出设置为249。除了输出通道个数为74的特征中0的个数不太均衡，其他所有层都满足特征通道0的个数相等的条件。实验表明，这样设计不但提高了模型性能，而且由于整个网络0的数量庞大且具有规律性，为进一步的模型剪枝及优化提供了可能性。由于本文采用奇数列向上移动、偶数列向下移动的方式对特征矩阵进行移动，所以计算网络中某一层中0的个数要对奇数列和偶数列分别进行单独处理。

偶数列0的个数为

式中，N为人体关节点总数，i为第i个关节点，C为通道总数，j为第j个通道数。

当N=7，C=13时，Meven=7，式(1)前半部分为0，后半部分为1+2+3+4+5+6，所以偶数列中0的个数Zeven= 21。

同理，奇数列0的个数为

最终整个网络的0的总个数为Zeven+Zodd。按上式计算的本文网络不同输出通道各层中0的个数在该层特征总数中的占比如表2所示。

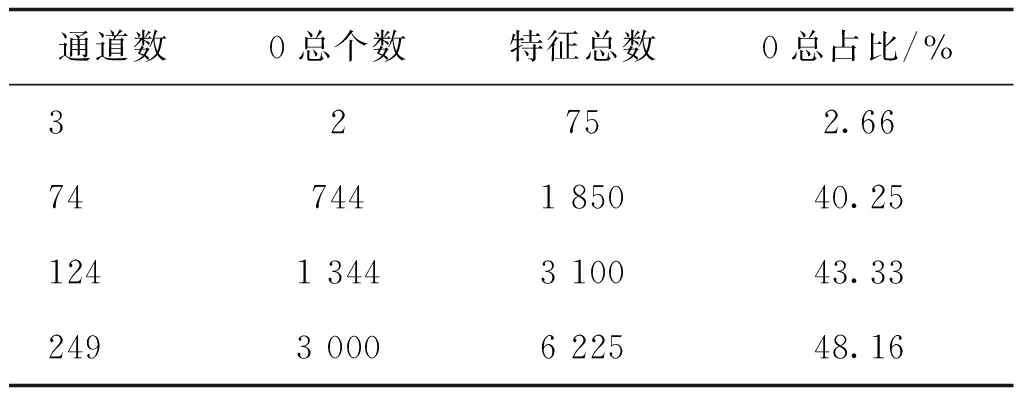
表2 网络不同输出通道各层中0的个数在该层特征总数中的占比Table 2 The proportion of number of 0 in each layer of different output channels of the network in the total number of features of this layer

从表2可以看出，0在整个网络中的占比非常大，本文工作不但能提高网络精度，而且为进一步的网络优化提供了可能性。本文网络结构都是10层，针对不同关节点个数只需要修改IntSparse-GCN参数即可，不需要修改任何其他参数。本文设计的网络结构与关节点个数是无关的，只是网络中每层的输入输出通道数与关节点个数有关。不同关节点个数不需要修改网络结构，只需要修改网络输入输出通道数即可。由于Northwestern-UCLA数据集中人体关节点个数为20，所以需要将网络输入输出通道改为20的整数倍。表3展示了适合于关节点个数为20的网络结构，描述了关节点为20时IntSparse-GCN各层网络输入输出情况。

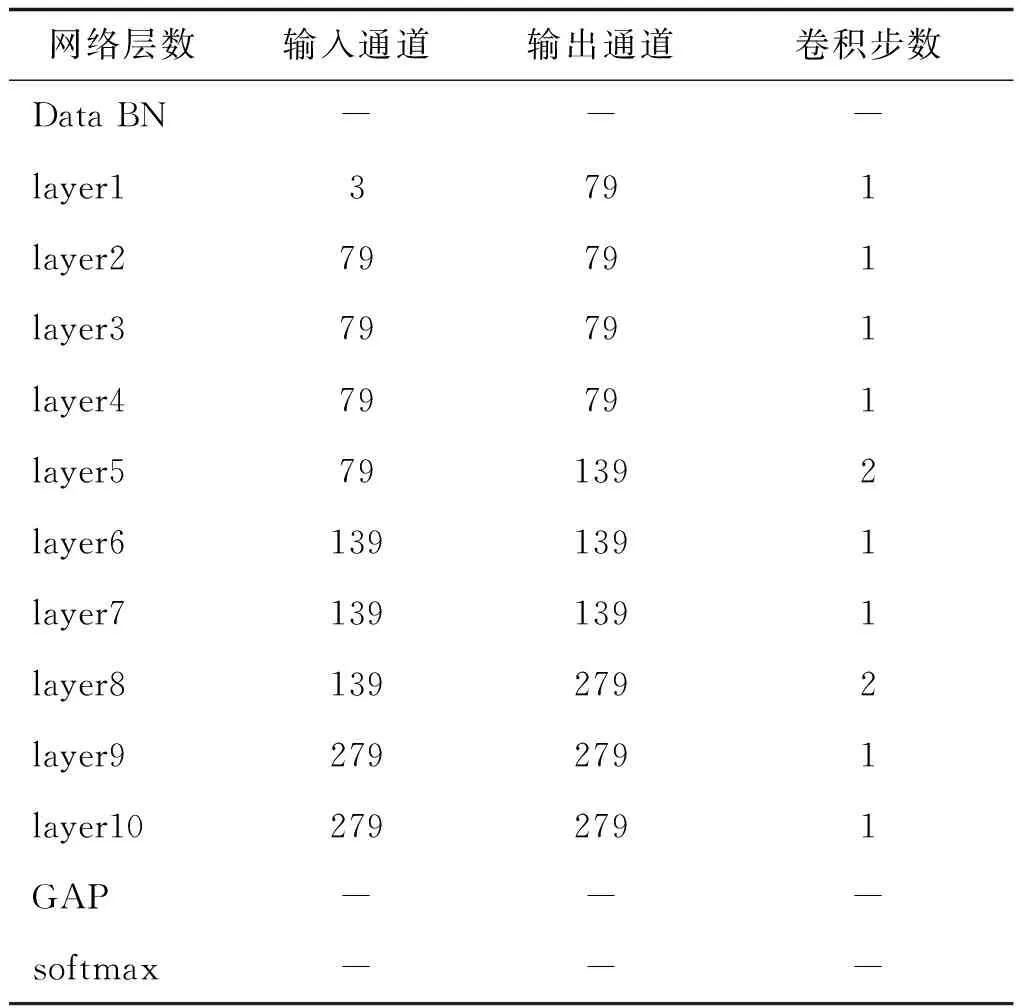
表3 关节点为20时IntSparse-GCN各层网络输入输出Table 3 The input and output description of each layer of IntSparse-GCN when the node is 20

2.2 Shift-GCN特征注意力机制优化

Shift-GCN提取关节点的特征shift之后，不同节点之间的连接强度是相同的。但由于人类骨骼的重要性不同，引入了一种自适应的非局部shift机制。计算shift特征和可学习掩码之间的元素乘积，通过一个可学习的自适应参数M增强重要关节部位的权重，具体计算为

(5)

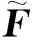
图5 不同层的tanh(M) + 1数据情况Fig.5 The tanh(M)+1 distribution of different layers((a)layer 1；(b)layer 3；(c)layer 5；(d)layer 7)

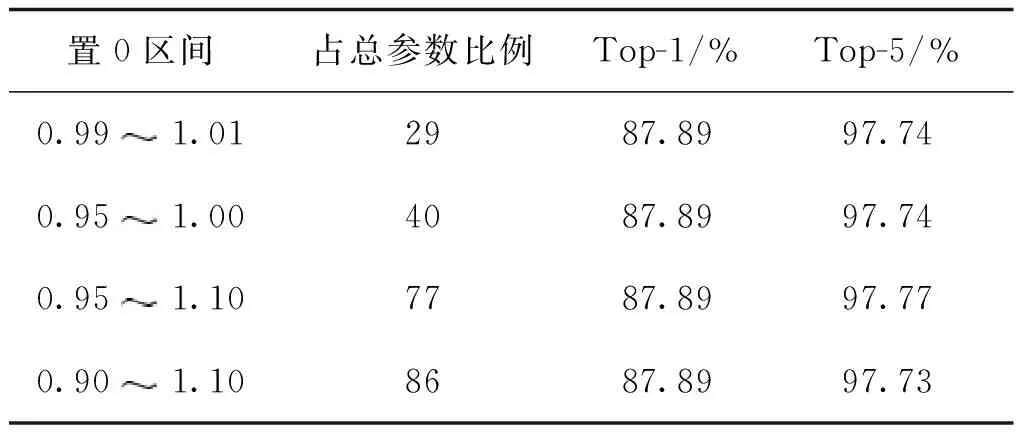
表4 不同区间置0后的精度变化情况Table 4 Accuracy changes after different intervals are set to 0

原模型的Top-1精度为87.88%。图6是Top-1精度为87.89%时网络第5层删除一定参数量后的数据分布情况。可以看出，删除不同程度的参数量后，精度都有所提升，删除的参数量越多，算法优化空间越大。

为此，设计了一个带超参数的循环自动化删除一定范围内M值的程序——最优模型自动搜索算法，通过该程序可以自动选取删掉一定范围内的M值，不但提高了模型分类精度，而且删掉的这部分参数不必再做乘法操作，节省了计算量。最优模型自动搜索算法具体实现过程如下：

1) 输入Original Model；

2) forliinL= {l1,l2,…,ln} do；

3) forrjinR= {r1,r2,…,rm} do；

图6 第5层删掉某些范围内的数值后不同置0空间的M的分布Fig.6 The distribution of M in different spaces of setting 0 after deleting some values in the range in the 5th layer((a)0.991.01;(b)0.951.00;(c)0.951.10;(d)0.901.10)

图7 不同区间为0的参数值在各层中的占比情况Fig.7 The proportion of parameter values with different intervals of 0 in each layer

4) for each layerLk∈Original Model do；

5) ifLkis Feature Mask then；

6)M= {x1,x2,…,xNV} is the value ofLk；

7)T= tanh(M) + 1；

8) fortg∈T= {t1,t2,…,tNV} do；

9) iftg>liandtg

10) updatexg= 0；

11) 测试每个新模型精度；

12) 选择精度最高的模型作为最终模型。

在实现过程中，通过设置tanh(M)+1的左右边界确定搜索范围，左边界搜索范围为0.90，0.91，…，1.00；右边界搜索范围为1.00，1.01，…，1.10。在不同区间内对所有M值置0，得到n个区间置0后的所有Top-1及Top-5的精度值，最终得到最高精度值更改后的模型。

3 实 验

3.1 数据集和评估指标

3.1.1 数据集

实验在NTU RGB+D(Shahroudy等，2016)和Northwestern-UCLA(Wang等，2014a)数据集上进行。NTU RGB+D数据集由56 880个动作样本组成，包含RGB视频、深度图序列、3D骨架数据和红外视频，由3部Microsoft Kinect v2相机同时捕获。RGB视频分辨率为1 920 × 1 080像素，深度图和红外视频均为512 × 424像素，3D骨架数据包含每帧25个主要身体关节的3维位置。3D骨骼节点信息通过Kinect相机的骨骼跟踪技术获得，由人体25个主要身体关节的3维位置坐标构成。骨骼追踪技术通过处理深度数据建立人体各关节坐标，能够确定人体的各部分(如手、头部或身体)及所在的空间位置。Northwestern-UCLA数据集也是由3部Kinect相机捕获，包含1 494个视频剪辑，涵盖10个类别。每类动作分别由10人完成。本文将前两台摄像机的样本作为训练样本，另一台摄像机的样本作为测试样本。

3.1.2 评估指标

使用Top-1及Top-5作为评价指标来计算分类的准确率。

3.1.3 实现细节

为了与之前方法进行比较，使用带有Nesterov动量(0.9)的SGD(stochastic gradient descent)训练140个epoch后终止学习。学习率设置为0.1，在第60、80和100个epoch时，学习率除以10。对于NTU RGB + D数据集，batchsize设置为64。对于Northwestern-UCLA，batchsize设置为16。消融研究中的所有实验均使用上述设置。深度学习的框架是PyTorch(Paszke等，2017)，本文网络使用NVIDIA 4 GeForce RTX 2080 Ti GPU进行训练。

3.2 消融实验

在NTU RGB + D数据集的X-sub上验证本文提出的IntSparse-GCN网络及最优模型自动搜索算法。分别对4流的精度提升情况进行对比分析，4流分别为joint、bone、joint motion和bone motion。不同改进模块对每个流的精度提升情况如表5所示。可以看出，添加不同模块后对各个流产生的影响是不同的，joint、bone和joint motion的Top-1精度分别提高了0.15、0.51和0.09，bone motion的Top-1精度降低了0.09。虽然bone motion有轻微精度下降，但是其他3个流的精度都有提升，4流融合后的精度是提升的。

为了更加详细地对本文算法进行验证，对4流融合后的精度情况进行验证分析，结果如表6所示，可以看出，与Shift-GCN模型相比，IntSparse-GCN+ M-Sparse模型在4个流上的精度均有不同程度的提升，在1 s、2 s和4 s的Top-1精度上比Shift-GCN分别提升了0.15、0.03和0.06。

3.3 与其他算法的对比分析

为了验证算法的有效性，在NTU RGB+D数据集的X-sub和X-view子集上及Northwestern-UCLA数据集上将本文算法与当前的先进方法进行对比分析，对比结果如表7及表8所示。

表7 本文算法与当前先进方法在NTU RGB+D数据集上对比结果Table 7 The proposed algorithm is compared with the state-of-the-art methods on the NTU RGB+D dataset

表8 本文算法与state-of-the-art方法在Northwestern-UCLA数据集上对比结果Table 8 The proposed algorithm is compared with the state-of-the-art methods on the Northwestern-UCLA dataset

从表7可以看出，本文算法与原始的Shift-GCN算法相比，计算量(floating-point operations per second，FLOPs)虽然略有增加，但仍为同一个数量级。然而，本文网络的精度在各个流上均有不同程度提升，且本文的特征是稀疏的，有近一半的特征值是0，为下一步优化模型提供了基础。

从表8可以看出，在Northwestern-UCLA数据集上，与Shift-GCN相比，在Top-1精度上，本文方法的1 s、2 s和4 s分别提升了0.39、1.06和2.17，超过了所有之前算法的性能。

3.4 算法效果可视化

为了进行更进一步的比较，使用混淆矩阵与之前算法的精度对比曲线来可视化算法的结果。图8显示了某些类别的混淆矩阵，可以看出，本文提出的IntSparse-GCN可以提高大多数类别的识别精度，尤其是对于一些容易混淆的类别，识别率得到了显著提高。例如，在Shift-GCN中pick up with one hand有9个样本识别成pick up with two hands，但是本文的IntSparse-GCN将错误识别的次数减少到1，识别正确个数明显增多。

图8 Northwestern-UCLA分类的混淆矩阵Fig.8 Confusion matrix for Northwestern-UCLA classification ((a) confusion matrix of Shift-GCN; (b) confusion matrix of IntSparse-GCN)

本文算法与先进算法的对比分析结果如图9所示。可以看出，本文算法在Northwestern-UCLA数据集上的精度提高最为明显，在NTU RGB+D数据集的joint和bone两个流上也有较明显的提高。

图9 本文算法与先进算法在不同数据集上的对比分析结果Fig.9 The results of comparison and analysis among the state-of-the-art algorithms and ours on different datasets((a) Northwestern-UCLA dataset; (b) NTU RGB+D dataset)

4 结 论

针对GCN网络较高的计算复杂度及Shift-GCN的特征冗余问题，本文从两个方面对网络进行优化，主要贡献及结论如下：

1)提出整数倍稀疏shift网络IntSparse-GCN。引入基于通道整数倍的空间shift算法，将移出通道部分的位置置0，使得特征通道中接近一半的特征值为0。这样的特征矩阵是具有强规律性的稀疏特征矩阵，不但提高了网络精度，还为进一步的模型剪枝优化提供了可能性。

2)对Shift-GCN中的mask掩膜进行研究分析，发现80%以上的参数都未起到注意力的作用。提出了自适应mask掩膜获取方法，不但提高了速度，精度也有所提升。

3)与现有一些经典的行为识别网络及Shift-GCN网络的对比实验表明，本文网络不但在各个流的性能上都有所提升，而且本文改进后得到的强稀疏性特征矩阵为模型速度的进一步提升提供了可能性。

虽然本文方法从两方面对Shift-GCN网络进行了优化，提高了识别精度，但通过混淆矩阵等实验发现，还是存在一定程度的错分及误分，主要是有一些类别的骨架信息不太准确，并且数据集中有一些非常相似的行为。因此，未来将尝试通过注意力机制等多种手段使相似行为能更好地区分，并利用特征矩阵的稀疏性对网络进行剪枝及量化，使网络能够移植到边缘计算设备上，优化后的网络在能源节约、信息安全和计算效率等方面将有较大的改善。