二维码位流长度最小化算法

袁泰凌，徐昆

1. 清华大学计算机科学与技术系，北京 100084； 2. 普适计算教育部重点实验室，北京 100084

0 引 言

快速响应矩阵码(quick response code，QR code)简称二维码，是一种正方形符号，广泛应用于商品识别、广告、在线支付和疫情防控等场景。二维码符号的最小单元是模块，即深色或浅色的小正方形。二维码的版本决定了每条边上的模块数量，如图1所示，二维码版本越大，每条边上的模块数量越多。

图1 不同版本的二维码示意图Fig.1 QR code examples with different versions((a) version 1; (b) version 6; (c) version 11)

二维码使用了纠错码，因此其对模块错误有一定纠错能力。减小二维码的版本能够在不减小模块大小的前提下节省面积，或者在不改变面积的前提下增大模块大小以提高模块正确识别的概率。

为了提高二维码的数据容量，现有研究工作主要采用了不兼容标准二维码的编码格式。例如使用彩色模块、修改模块排布、修改位流编码步骤等。这些方案都需要使用专门的扫码器才能读取。考虑到扫码用户一般有通用的标准二维码扫码器，而不一定有专门的扫码器，因此这些二维码的普适性较差。如何在兼容二维码标准的前提下最大化数据容量是一个待解决的问题。

与上述研究工作不同的是，本文在符合二维码标准的前提下最小化位流长度，从而最大化数据容量。本文算法输出的位流与标准算法(国家质量技术监督局，2000)、开源编码器ZXing(https://code. google.com/p/zxing)、商业编码器“草料二维码生成器”(http://cli.im/)相比，长度相同或更短。一方面，信源编码问题转换为动态规划问题，提出了计算最短位流的算法；另一方面，针对常见的统一资源定位符(uniform resource locators，URL)类型数据，进一步减小位流长度，提出了统一资源定位符的最短位流计算算法。

1 相关工作

关于二维码数据容量的研究主要分为以下几类：

1)通过增加模块的颜色种类提高数据容量。包括使用RGB 3个色彩通道表示3倍数据(Blasinski等，2013；Meruga等，2015)、使用3种荧光材料表示3倍数据(Abdolahi等，2019)、使用4种特定颜色表示log24=2倍数据(Melgar等，2012)、使用至多214种颜色表示至多14倍信息(Galiyawala和Pandya，2014)。Yang等人(2018)指出颜色混叠效应会导致彩色二维码较难解码，并基于支持向量机(support vector machine，SVM)提出一种针对彩色二维码的解码算法。贾丹等人(2017)基于k-means算法识别彩色二维码。由于彩色二维码是自定义的编码格式，因此标准二维码解码器无法解码彩色二维码，而需要使用定制的解码器。

2)在二维码中隐藏私有信息。Tkachenko等人(2015，2016)提出的双级别二维码(two-level QR codes)在标准二维码的黑色模块上添加纹理，其中标准二维码编码主要信息，纹理编码私有信息；标准二维码解码器可以读取主要信息，定制的解码器可以读取私有信息。Barron等人(2020)提出的双重调制二维码(dual modulated QR codes)将标准二维码的黑色模块由正方形替换成椭圆形，用椭圆的方向编码隐私信息。标准二维码解码器可以读取公开信息；当相机与二维码距离较近时，定制的解码器可以从模块方向中读取隐私信息。这两种修改模块纹理或模块形状的方法损害了每个模块的识别率，使得二维码的主要信息更难识别。

3)压缩输入数据。邹敏等人(2015)使用Huffman算法压缩输入数据；Abas等人(2017)使用 Gzip、Zip等多种压缩算法压缩输入数据，并将压缩后的二进制数据用base64格式编码成字符串作为二维码编码器的输入。对于这类编码算法，标准二维码解码器会读取到压缩后的数据，而不知道如何翻译这些数据。Victor(2012)提出的二维码和陈元枝等人(2015)提出的二维码均同时使用了彩色模块和压缩数据两项技术共同提高数据容量。杨康等人(2017)基于汉字字频提出了一种针对汉字的变长编码方案，这也属于在信源处对位流编码方案进行了压缩。郑志学(2020)提出同时使用压缩和加密两种技术生成防伪二维码。

4)通过自定义模块排布方式增大编码区域的面积占比。Villn等人(2006)提出了一种多级别二维条码。这种条码格式没有位置探测图形等功能图形，因此编码区域比标准二维码更大。具有较大编码面积并且同时具有较美观外表的二维条码格式有PiCode(picture-embedding 2D barcode)(Chen等，2016)和RA Code(robust and aesthetic code)(Chen等，2018)等。

除上述几类工作外，还有一些旨在提高二维码容量的研究工作。Yuan等人(2019)提出了双层二维码，利用视角差在左右两个方向显示不同的二维码，并且可以用标准二维码解码器解码。但是双层二维码要求相机处于特定的角度范围才能解码，而且解码成功率比标准二维码低。Chou和Wang(2020)提出了嵌套二维码，在外层二维码图案的内部嵌入了一个尺寸更小的内层二维码，标准扫码器可以分别从外层二维码和内层二维码中获取不同消息。但是内外两个二维码的尺寸差异较大，导致较小的二维码较难解码，而且用户不易选择扫描哪个二维码。

综上所述，目前没有一种方法能在兼容标准二维码解码器且不影响纠错能力的前提下提升数据容量。

2 位流编码格式

本节介绍二维码标准GB/T18284-2000(国家质量技术监督局，2000)所采用的位流编码格式。二维码有40个版本，从版本1到版本40。版本越大，模块数量越多，码字总数越多。同时，二维码有4个纠错等级，即L、M、Q和H，分别代表纠错能力大约7%、15%、25%和30%。纠错等级越高，数据码字占码字总数的比例越小。对于给定的版本和纠错等级，数据码字数量可查表得到。每个数据码字表示8个二进制位，因此，位流长度不能超过数据码字数量的8倍。

位流包含若干段(segment)，每一段分别编码了一部分数据或编码了附加特性(additional features)。每个编码数据的段分为3部分，从前往后分别是模式指示符(mode indicator)、字符计数指示符(character count indicator)和数据。模式指示符表示这一段采用的编码模式(mode)。编码模式共有4种，即数字模式、字母数字模式、8位字节模式和中国汉字模式，占用4位。其中，数字模式只能编码数字；字母数字模式可以编码大写字母、数字和9种符号；8位字节模式可以编码任意二进制数据；中国汉字模式只能编码中国汉字。特别地，中国汉字模式的模式指示符之后有中国汉字子集指示符，长度是4位，只有一种取值0001，表示GB2312 字符集。字符计数指示符表示这一段编码数据的长度。字符计数指示符占用的位数随模式和二维码版本变化，可查表得到。在数字模式下，每3个数字字符编码成10位；如果数据长度不是3的整数倍，则剩余的 1个字符编码成4位，或者剩余的2个字符编码成7位。字母数字模式、8位字节模式和中国汉字模式编码数据所需位数如表1所示。附加特性有专门的格式，可编码结构链接(structured append)信息、扩充解释(extended channel interpretation, ECI)信息，不用于编码字符。本文所称的位流不包含终止符、填充位和填充码字。

表1 各模式编码n个字符所需位数Table 1 The number of bits to encode n character in each mode /bit

算法和实验不考虑中国汉字模式，原因如下：1)中国汉字模式与国际二维码标准不兼容。2)解码器即使支持中国汉字模式(例如微信和支付宝的扫一扫、开源解码器ZXing等)，也对含中国汉字模式的二维码解码有误。3)在实验获取的2 000多个二维码中，只有一个二维码使用中国汉字模式，其他二维码的汉字是通过代码页(例如UTF-8、GB2312等)转换成多个字节后用8位字节模式编码的。

一种简单的位流编码算法是使用单一模式编码所有数据，并且尽量使用数据位数少的模式，即数字模式优先，字母数字模式次之，不能用以上两种模式编码时使用8位字节模式编码，开源编码器ZXing使用这种算法。对各种模式和纠错等级，二维码标准以表格形式给出了各版本二维码能容纳的字符数量，编码器可根据该表格决定二维码的版本。刘悦和刘明业(2005)指出了上述表格中的错误。

与使用单一模式相比，在不同模式之间切换可能得到更短的位流。例如，数字字符可以用3种模式编码，使用数字模式编码的数据位数最少，字母数字模式编码的数据位数次之，8位字节模式编码的数据位数最多。然而，如果前一个字符使用8位字节模式编码，那么切换到数字模式需要添加模式指示符和字符计数指示符，反而可能使总体位流变长。最优位流编码需要权衡总体数据位数和切换模式的开销。二维码标准的附录给出了“位流长度的最优化”方法。这是一种基于规则的方法，根据连续同类型字符长度(例如连续数字字符数量)切换模式，但该算法并不是最优算法。

3 提出的算法

3.1 位流长度最小化

给定长度为l(l≥1)的输入数据，输入数据的第i个字符记做si(1≤i≤l)，si是8位字节。目标是用最短的位流编码输入数据。

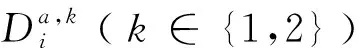
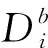
因此，Di是这6个符号的最小值，即

(1)

用Σm(m∈{n,a,b})表示对应模式的字符集，有包含关系Σn⊆Σa⊆Σb。用hm(m∈{n,a,b})表示对应模式的模式指示符与字符计数指示符的位数之和。

(2)

再考虑第i(2≤i≤l)个字符用数字模式编码且是所在段的第k′(k′ ≡ 2 mod 3)个字符的情况。只有当第i-1个字符用数字模式编码且是所在段的第k′′(k′′ ≡ 1 mod 3)个字符，且第i个字符沿用该数字模式段时才可以得到符合条件的编码，因此

(3)

同理可得

(4)

(5)

(6)

(7)

特别地，对于第1个字符，可得

(8)

至此，位流长度最小化问题已转换为动态规划问题。

引理1 给定版本和输入数据，可以在O(l)时间内计算最短位流。

定理1 给定输入数据和纠错等级，可以在O(l)时间内计算最短位流及对应的版本。

输入：数据s、纠错等级ECL，

输出：位流BS、版本V，

1) function minimum_BS(s,ECL)，

2) forV= 1 to 40 do，

3) ifV∈{1, 10, 27} then，

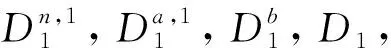
5) fori= 2 toldo，

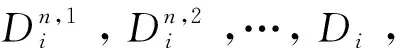
7)BS←长度等于Dl的位流，

8) ifDl≤最大位流长度(V,ECL) then，

9) returnBS,V，

10) return 编码失败。

3.2 统一资源定位符的最优编码

统一资源定位符通常由协议(scheme)、主机 (host)和路径等字段组成。常见的统一资源定位符协议包括超文本传输协议(hypertext transfer protocol，HTTP)和文件传输协议(file transfer protocol，FTP)等。

根据RFC(request for comments)1738统一资源定位符规范，协议字段对大小写不敏感。根据RFC 1035域名规范，主机字段对大小写不敏感。因为小写字母只能用8位字节模式编码，而大写字母既可以用8位字节模式编码，又可以用字母数字模式编码，所以将对大小写不敏感的字符转换成大写字母可以缩短位流长度。例如“http://example.com/”和“HTTP://EXAMPLE.COM/”是等效的统一资源定位符，前者最短位流长度是164，后者最短位流长度是118。

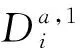
(9)

式中，uc(si)表示si的大写形式(upper case)，若si不是字母，则定义uc(si)=si。

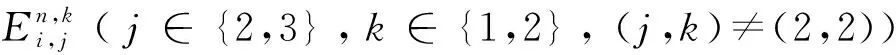
因为用8位字节模式编码转义序列的任一字符一定会使总体位流长度比直接编码转义字符更长，所以无需考虑转义序列的任一字符由8位字节模式编码的情况。因为最短位流的任意相邻两段的模式一定不同(否则，将它们合并为一段将更短)，所以无需考虑任意连续两段模式相同的情况。用c(si)表示字符si的转义序列末尾属于数字字符集的字符数量，值域是{0,1,2}。对于第i(2≤i≤l)个字符，如果该字符可以转义，则有

(10)

(11)

若c(si)=2，则

(12)

(13)

(14)

若c(si)≥1，则

(15)

(16)

(17)

(18)

若第i个字符属于字母数字模式字符集，或者是对大小写不敏感的字段的小写字母，则直接用字母数字模式编码必然比转义后编码更短，无需转义优化。此外，如果输入数据已经经过了转义，且第i个字符是转义序列中的字符，则按照规范不能对si再次转义，不能应用转义优化；此时si对大小写不敏感，可以应用大小写不敏感字段优化。综合上述条件，若第i个字符属于协议特定部分，且不属于字母数字模式字符集，不是转义序列中的字符，不是对大小写不敏感的字段的小写字母，则重新定义为

(19)

定理2 给定统一资源定位符和纠错等级，可以在O(l)时间内计算大小写和转义意义下等效的位流中最短的位流及对应的版本。

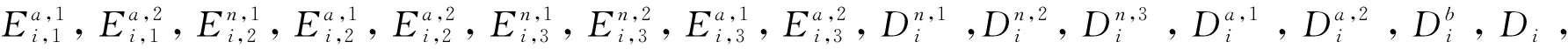
输入：数据s、纠错等级ECL，

输出：位流BS、版本V，

1 function minimum_BS_improved(s,ECL)，

2 if is_not_URL(s) then，

3 return minimum_BS(s,ECL)，

4 forV= 1 to 40 do，

5 ifV∈{1, 10, 27} then，

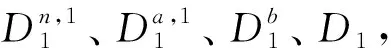
7 fori= 2 toldo，

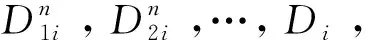
10BS←长度等于Dl的位流，

11 ifDl≤最大位流长度(V,ECL) then，

12 returnBS,V，

13 return 编码失败。

4 实 验

4.1 参与比较的算法

二维码标准中的位流长度最优化算法(以下简称标准算法)定义了字母数字模式专有子集ΣbΣa以及字符模式专有子集ΣaΣn。编码时，根据当前字符所属的字符集(或专有子集)及连续的来自相同字符集(或来自相同专有子集)的字符数量切换编码模式。例如输入数据“abc123456def”，编码第4个字符时，因为连续6个字符属于数字字符集，因此切换到数字模式，位流长度比全部用8位字节模式编码短2位。标准算法有可能陷入局部最优。例如输入数据“1234567Ab”，用数字模式编码“1234567”，用8位字节模式编码“Ab”是最优的；但是标准算法使用字母数字模式编码“A”，用8位字节模式编码“b”。标准算法与最优编码相比，增加了字母数字模式的模式指示符4位、字符计数指示符9位，只减少了数据位数2位，总体位流长度增加了4+9-2=11。除中国汉字模式外，二维码标准GB/T18284：2000中的位流长度最优化算法与国际二维码标准ISO/IEC18004:2000相同。因为国际二维码标准已更新为ISO/IEC18004:2015，位流长度最优化算法有所改进，所以实验对比的标准算法是国际标准ISO/IEC18004:2015。

开源编解码器ZXing的位流编码算法比较简单。该算法使用单一编码模式，如果所有字符都属于Σn，则使用数字模式编码；否则，如果所有字符都属于Σa，则使用字母数字模式编码；否则，使用8位字节模式编码。以下将这种使用单一编码模式编码所有数据的算法称为单模算法。

据黑盒测试，商业编码器“草料二维码生成器”的位流编码算法是对于所有输入数据都使用8位字节模式编码。因为这种算法输出的位流一定不比单模算法短，所以实验不比较这种算法。

单模算法、标准算法和最小化算法对几种特定的输入数据编码的位流长度如表2所示。

表2 3种算法输出位流长度举例Table 2 Examples of output bit stream length of three algorithms /bit

4.2 二维码测试集

为了获取实际场景的二维码图像，实验使用百度、搜狗、360、谷歌、必应(国内版和国际版)和雅虎等图像搜索引擎分别搜索“二维码”和“QR Code”，搜索日期是2021年2月3日。对下载的每幅图像使用开源解码器ZXing解码。部分图像无法解码，原因主要包括：图像主体内容不是二维码、图片含多个二维码导致解码器无法定位、二维码污损或遮挡和二维码模块规格不标准等。位流互异或纠错等级互异的二维码均视为互异的二维码。去除ZXing无法解码的图像后，得到2 289个互异的二维码。再去除1个含中国汉字模式的二维码、6个含Kanji模式(一种只在国际标准里定义的模式)的二维码后，测试集包含2 282个互异的二维码。根据二维码数据是否为统一资源定位符，将测试集划分为非URL测试集和URL测试集。非URL测试集包含603个二维码，URL测试集包含1 679个二维码。实验只考虑了协议为http、https、ftp、ftps、mailto的统一资源定位符。测试集中位流长度属于各区间的二维码样本数量如图2所示。

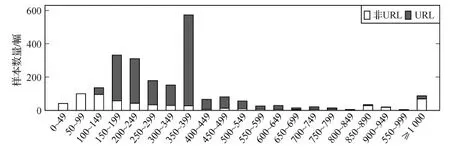
图2 测试集位流长度分布Fig.2 Distribution of bit stream length in the test set

4.3 位流长度与版本的优化效果

对测试集中的每个二维码分别重新编码。部分二维码包含附加特性。在重新编码过程中，所有附加特性段保留原样，且附加特性段在字符数据中的位置保持不变。表3和表4比较了标准算法、单模算法、位流长度最小化算法和统一资源定位符的最优编码算法输出的位流的平均长度，以及各算法输出的位流长度相较标准算法有所减小的二维码数量占测试集的比例。由于位流长度的减小需要通过二维码版本的减小才能反映到最终印刷品的面积或印刷质量上，因此表中还给出了各编码算法输出的二维码版本相较标准算法有所减小的二维码占比，其中标准算法输出的版本等于1的二维码不计入分母。实验数据表明，对于非URL测试集(包含603个二维码，其中419个二维码标准算法输出的版本大于1)，本文算法将平均位流长度减小了0.4%，减小了其中55个(9.1%)二维码的位流长度，减小了其中5个(1.2%)二维码的版本；对于URL测试集(包含1 679个二维码，其中1 657个二维码标准算法输出的版本大于1)，本文算法将平均位流长度减小了13.9%，减小了1 652个(98.4%)二维码的位流长度，减小了525个(31.7%)二维码的版本。图3给出了本文提出算法输出的二维码版本比标准算法小的示例。

表3 在非URL测试集上位流长度或版本减小的二维码占比Table 3 The ratio of QR codes of which bit stream length or version can be reduced on the test set with non-URL data

表4 在URL测试集上位流长度或版本减小的二维码占比Table 4 The ratio of QR codes of which bit stream length or version can be reduced on the test set with URL data

图3 本文提出算法减小二维码版本的示例Fig.3 QR code examples of which version is reduced by the proposed algorithm((a)initial QR code;(b)standard algorithm;(c)minimization algorithm;(d)URL minimization algorithm)

4.4 扫码成功率的优化效果

实验对比了参考二维码(指标准算法生成的二维码)与最小二维码在不同模糊程度下的扫码成功率。用标准差为σ的二维高斯核对二维码图像进行模糊；其中，图像的分辨率为300 × 300像素，二维码占据图像正中间的200 × 200像素。分别统计2 282幅参考二维码图像和2 282幅最小二维码图像的扫码成功数量，统计结果如图4所示。实验数据表明，当σ在[1.7, 5.5]范围时，本文算法将扫码成功图像数量提高了10幅以上；当σ在[3.6, 4.8]范围时，本文算法将扫码成功图像数量提高了100幅以上。

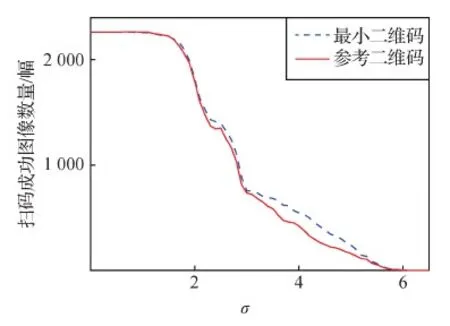
图4 扫码成功图像数量与高斯核的标准差的关系Fig.4 The number of successfully scanned images against kernel standard deviation of Gaussian blur

4.5 统一资源定位符的最优编码的消融实验

统一资源定位符的最优编码算法包含两个优化：1)大小写不敏感字段优化(式(6))；2)转义优化(式(8))。实验在URL测试集上测试了4种优化组合输出的位流长度和二维码版本相较标准算法减小的二维码占比，实验结果如表5所示。实验数据表明，单独进行大小写不敏感字段优化或转义优化都有优化效果。同时启用两项优化时，得到的平均位流长度最小，位流长度减小和版本减小的二维码占比最大。对于URL测试集，最小化算法只将平均位流长度减小了0.5%，而URL最优编码算法将平均位流长度减小了13.9%；最小化算法只减小了175个(10.4%)二维码的位流长度，而URL最优编码算法减小了1 652个(98.4%)二维码的位流长度；最小化算法只减小了21个(1.3%)二维码的版本，而URL最优编码算法减小了525个(31.7%)二维码的版本。

4.6 运行时间

实验平台的CPU是Intel Core i7-10700，内存大小为32 GB；算法用C++实现。对于非URL测试集中的每个输入数据，重复调用位流长度最小化算法10 000次，并记录这10 000次运行时间的平均值。运行时间与输入数据的长度的关系如图5所示。实验使用相同的方法测试了URL最优编码算法对URL测试集中的数据进行编码的时间，如图6所示。

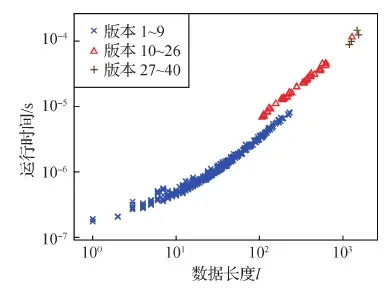
图5 非URL数据的编码时间与数据长度的关系Fig.5 Encoding time against data length for non-URL data

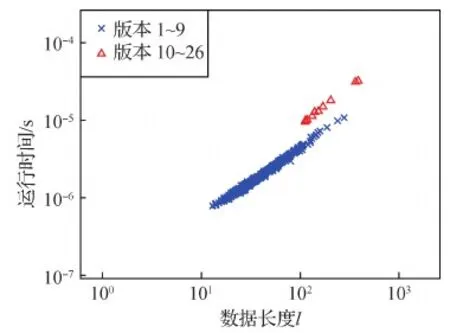
图6 URL数据的编码时间与数据长度的关系Fig.6 Encoding time against data length for URL data

5 结 论

本文解决了二维码位流长度最小化问题，提出的二维码位流长度最小化算法可以计算最短位流。对于URL类型数据，URL最优编码算法进一步减小了位流长度，可以计算出大小写和转义意义下等效的统一资源定位符的最短位流。实验结果表明，本文算法输出的位流长度最短，输出的二维码版本最小，在一些实际场景中可以减小二维码的版本，并且具有运算速度快的特点，其时间复杂度的上界与输入数据长度呈线性关系。此外，本文算法易于使用，用户只需输入数据和纠错等级即可，无需调节任何参数。

需要说明的是，本文只针对二维码提出了位流长度最小化算法。Data Matrix和PDF417等其他条码类型也使用与二维码类似的编码结构，但是编码细节存在差异，本文算法不能直接用于其他条码类型的位流编码。

在未来的工作中，可将本文算法的思路经适配后用于最小化Data Matrix和PDF417等其他条码类型的位流长度。同时，本文算法思路对于其他条码类型是否有效也有待验证。