矩阵方程的秩约束最小二乘对称半正定解及其最佳逼近
2022-08-08喻思婷彭靖静彭振赟
喻思婷,彭靖静,彭振赟
(桂林电子科技大学 数学与计算科学学院,广西 桂林 541004)

矩阵方程AX=B及其最佳逼近是研究成果最多、最为成熟的一类矩阵方程。Bjerhammar[1]利用广义逆给出矩阵方程有解的充分必要条件及一般解的表达式;廖安平[2]、Higham[3]、Allwright[4]分别讨论了线性流形约束解、最小二乘对称解和对称半正定最小二乘解;Dai[5]利用矩阵奇异值分解方法给出有对称解的充分必要条件及有解时一般解的表达式;张磊等[6]讨论了线性流形约束双对称解;Xie等[7]、彭振赟[8]分别讨论了反对称次对称解和子矩阵约束解;Li等[9]讨论了列元素约束最小二乘解;徐安豹等[10]讨论了范数约束最小二乘解;彭金风等[11]讨论了D-对称半正定最小二乘解;李媛等[12]、张四保等[13]分别讨论了可双对称化解和主理想环上的对称解。本文讨论矩阵方程AX=B的秩约束最小二乘对称半正定解及其最佳逼近的数值计算方法。问题描述如下:

(1)
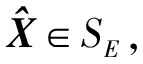
(2)
基于矩阵的奇异值分解和对称矩阵的谱分解,本文给出问题1和问题2有解的充分必要条件以及问题1和问题2有解时解的一般表达式,给出求解最佳逼近解的计算步骤,用数值例子说明结果的正确性。
1 问题1和2的解
引理1[14]设E、G分别是r×r阶和(n-r)×(n-r)阶矩阵,则
是对称半正定矩阵的充分必要条件为
引理2[15]设F∈Rn×n,D=diag(d1,d2,…,dn)>0,则最小二乘问题
存在唯一解,且其唯一解可以表示为
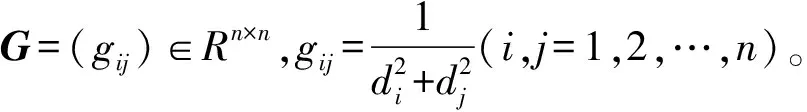
式中:P∈ORn×n,Σ1=diag(λ1,…,λr)>0,Σ2=diag(λr+1,…,λn)≤0,则最小二乘问题
存在唯一解,且其唯一解可以表示为
引理3设矩阵A的奇异值分解为
(3)
式中:U=(U1,U2)∈ORm×m;U1∈Rm×r;V=(V1,V2)∈ORn×n;V1∈Rn×r,Σ=diag(σ1,σ2,…,σr)>0;r=rank(A)。令
(4)

(5)
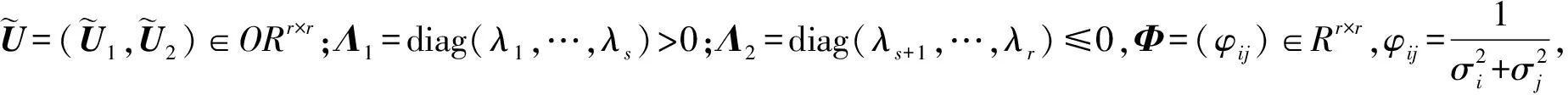
(6)
有解的充要条件是
(7)
并且有解时其解可以表示为
(8)

证明令
(9)
由范数的正交不变性可得
因此,
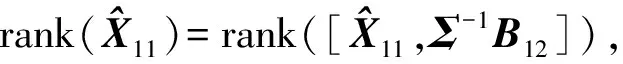
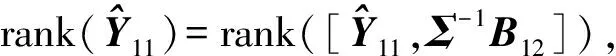

(11)
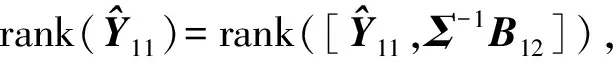

(12)
由式(10)、(12)有
(13)

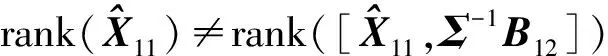
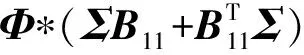
(14)
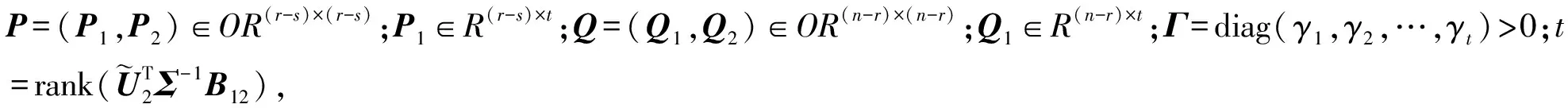
(15)
s+2t≤p≤n-r+s+t。
(16)
并且当式(15)、(16)成立时,问题1的解可以表示为
(17)
式中:
(18)
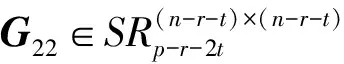
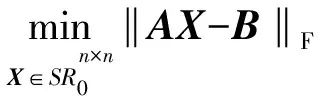
则由式(8)可知
(19)
令
则由式(14)、(19)可知
(20)
令
则有
(21)
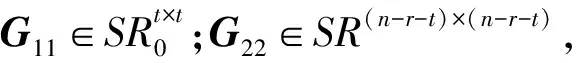
(22)
式中
由式(22)和引理1可得如下结果:
① min rank(X)=s+2t⟺G11=0,G12=0,G22=0。

由①、②、式(8)、(22)及引理1可知,问题1有解的充分必要条件是式(15)、(16)成立,并且当式(15)、(16)成立时,其解可以表示为式(17)。证毕。
为了方便给出问题2的解,先给出如下引理。
引理4[16]假设对称矩阵M的谱分解为
式中:U∈ORn×n;Σ1=diag(σ1,σ2,…,σr);σ1≥σ2≥…≥σr>0;Σ2=diag(σr+1,σr+2,…,σn);0≥σr+1≥…≥σn, 则最佳逼近问题
有解的充分必要条件是0 (23) (24) (25) (26) (27) s+2t≤p≤s+2t+r2。 (28) 并且有解时其解可以表示为 (29) 证明注意到 由式(17)和Frobenius范数的正交不变性有 (30) 由式(23)、(30)可得 (31) (32) 类似定理1的证明可知问题(31)有解的充分必要条件是 且有解时其解可以表示为 由引理4可知问题(32)有解的充分必要条件是式(28)成立,且有解时其解可以表示为 证毕。 基于第1章讨论结果,本章给出求解最佳逼近问题2的唯一解的计算步骤。 ① 输入矩阵A、B、X*和正整数p; ② 按式(3)将矩阵A进行奇异值分解; ③ 按式(4)将矩阵UTBV进行分块; ⑥ 若式(15)、(16)满足,则转第⑦步,否则,问题2无解; ⑨ 若式(27)、(28)满足,则转第⑩步,否则,问题2无解; 例1给定正整数p=4,矩阵A、B和X*如下(Matlab格式生成,A=randn(13,11),B=randn(13,11),X*=randn(11,11)): 矩阵方程的秩约束解在最优化控制、鲁棒优化和统计分析等领域有重要应用[17-18]。基于矩阵奇异值分解和对称矩阵的谱分解,本文给出矩阵方程AX=B有秩约束最小二乘对称半正定解及其最佳逼近解的充分必要条件及有解时解的一般表达式,给出求解最佳逼近解的计算步骤,用数值例子说明结果的正确性。还有诸多有待于进一步研究的问题,如AXB=C和AX+XB=C等矩阵方程的秩约束最小二乘对称解、对称半正定解、非负解问题等。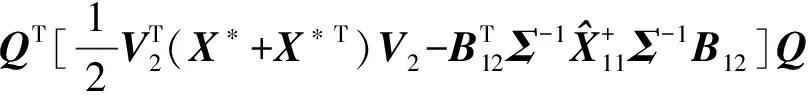
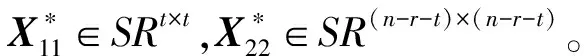

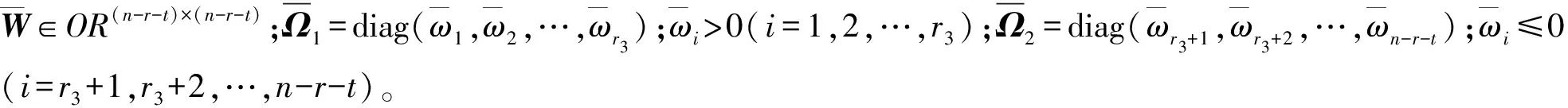
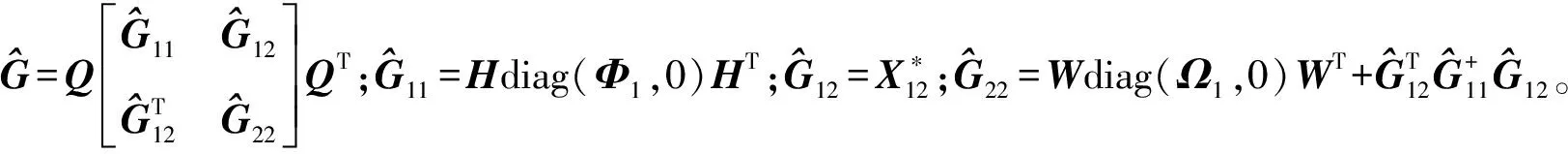


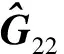
2 算法与数值例子
3 结语
