基于采样计算的差分N通道滤波器

钟 辉，宋树祥，岑明灿，蔡超波，蒋品群，刘振宇

(广西师范大学 电子工程学院，广西 桂林 541004)

随着不同无线电频率标准的使用，无线通信系统得到迅速发展[1-10]。为了衰减噪声和干扰信号，通常采用表面声波(SAW)或体声波(BAW)滤波器。但由于规模和成本的原因，表面声波(SAW)或体声波(BAW)滤波器在未来收发机中将不再是合适的选择[11]。因此引入了软件定义的无线电接收机，希望取代只对应于某些频带宽度的滤波器。N通道滤波器因其精确控制中心频率，同时具有高品质因数的特点，成为可调模拟前端接收机中基本模块的一个有吸引力选择[12]。

近年来，N通道滤波器逐渐引起了广泛的研究兴趣且取得不小进展：Mirzaei等[13]对M相带通滤波器进行分析，改进电路结构，推导出滤波器传递函数的精确表达式；Ghaffari等[14]利用差分结构减少时钟泄漏，抑制时钟谐波的选择性;Pavan等[15-18]利用伴随网络确定等效LTI系统的脉冲响应，推导了开关RC电路中完整电容电压模型，确定了并联电容和串联电感对N通道混频器和滤波器性能的影响,简化了电路的分析。然而，由于采用N个不重叠的开关时钟进行信号采样，N通道滤波器有2个主要缺点，分别为谐波选择性(HS)和谐波折返(HFB)[19]。目前，研究人员已经做了许多工作来减少N通道滤波器中的多次谐波和折返效应：Hemati等[20]提出一种多个N通道滤波器叠加的电路，减少了HFB问题；Tavassoli等[21]使用带通反馈，对偶次谐波进行抑制；Xu等[22]通过多相信号合成结构以谐波矢量叠加的方式消除了谐波；Hazrati等[23]通过2个受开关控制的LC带阻滤波器进行预滤波，改善了N通道滤波器中的HFB，采用单端输入到差分输出的结构，抑制了3k次谐波[24]。虽然这些方法在一定程度上能改善滤波器的主要缺陷，但都不能很好地解决上述问题。

本文采用一种利用差分采样电路消除多余谐波通带并减小谐波折返的方法。利用差分结构消除偶次谐波并将整个滤波器的规模缩小一半；通过多个时钟信号对通道进行采样输出，并按一定比例因子叠加，消除了某些奇数倍时钟频率处的谐波通带，如3fs、5fs。同时，本文采用开关时钟不同的2个N通道叠加的电路结构，减小了折返效应。

本文其余部分组织如下：第1章给出N通道滤波器的概述，采用傅里叶级数展开法，对理想N通道滤波器的频率响应及其HFB进行综合分析。第2章讨论和总结用于谐波抑制和消除折返效应的N通道滤波器的数学分析和基本概念。第3、4章介绍电路实现和仿真结果，以及与现有技术的比较。第5章给出结论。

1 N通道滤波器基本理论

传统N通道滤波器基本结构如图1(a)所示，电路中每个开关都作为混频器工作，输入射频信号Vin经过第一个开关混频下变频到基带，在基带进行滤波，然后将滤波后的信号上变频到相同的射频频率。因此，该电路可以看作是一个通过改变时钟频率来调节中心频率的带通滤波器。H(f)表示基带滤波器的传递函数。开关时钟信号S1～SN采用图1(b)所示的N个具有不同相位的非重叠时钟，时钟为高电平时，开关导通。

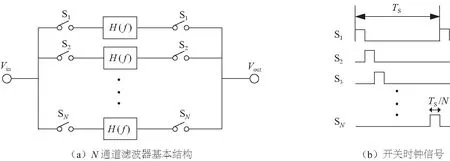
图1 传统N通道滤波器

图1(a)所示的传统N通道滤波器的输出Vout(t)可表示为

(1)

式中Si,1(t)、Si,2(t)分别表示电路第i个通道左侧与右侧的时钟信号，这些信号可以定义为:

(2)

(3)

为了在频域中表示输出信号，Si(t)的傅里叶级数(图1(b))可以写成如下形式:

(4)

(5)

利用傅里叶变换特性和时钟信号的傅里叶级数展开，图1(b)中N通道滤波器的输出信号在频域中可表示为:

(6)

由式(6)可知，虽然传统N通道滤波器可以提供较好的可调性，但它仍然有2个缺点:谐波选择性(HS)和谐波折返(HFB)。谐波选择性意味着滤波器在频率为nws(n=2,3,4…)的周围有多余的通带。谐波折返效应是指w=(kN±1)ws处的输入信号叠加在ws处的所需信号之上的现象。这2个缺点会在整个滤波过程中引入过多的谐波，严重降低滤波器的性能。

忽略频率折返的影响(n+m=0)，输出信号可表示为

(7)

为了模拟折返效应，式(6)可以改写为

(8)

式中：Hn(f)是输入频率为(n±1)fs时的传递函数(ws=2πfs)；fs是电路时钟频率。当n=0时，H0(f)为没有频率偏移的滤波器的频率响应。

HFB是一个过程，在这个过程中，滤波器将所需频率以外的频率周围噪声和干扰信号转换到其通带中。一般情况下，(N±1)fs是N通道滤波器折返效应最强的谐波。通过增加滤波器通道的数量，提高最强折返谐波的频率和增大与所需通带间的距离，可减少折返效应[25]。但是增加通道数量会使N通道滤波器实现难度增加，特别是在高频处。因此，本文希望在不增加时钟频率的情况下减少HBF。

2 电路设计

2.1 谐波抑制

为了抑制滤波器的谐波，本文采用一种采样计算的方法。以8通道滤波器为例，在任何时刻只有一个电容连接到输出节点上。假设时间常数τRC≫Ts/N，通道采样时电压可视为输入电压在电容器工作时间内的平均值，如图2(a)所示，每个输出阶跃电压都是各路电容非重叠周期采样的结果[14]。由于8通道滤波器使用互不重叠的连续时钟信号进行采样，每个周期内阶跃电压之间的相位相差45°，在频域中偏差exp(jπ/4)，写入相量图，如图2(b)所示。

图2 采样输出及向量

常用的N通道滤波器有传统单端N通道滤波器和差分N通道滤波器。差分结构旨在消除偶数谐波响应。每个路径都是差分输入和差分输出，中间包含一个电容，该电容两端各连接到2个相反相位的驱动开关[13]。对于偶数倍时钟频率附近的输入信号，稳态时电容器上不会存储任何电荷，输出端也不会出现干扰信号。差分N通道滤波器的传递函数可以写成[26]

F(w)=(1-exp(jnπ))Vout(w)。

(9)

式中n为谐波倍数。由式(9)可推导出，当n为偶数时，F(w)等于0，这意味着消除了时钟频率偶数倍数的所有谐波。

为了消除奇次谐波，同时保持信号不受干扰，在传统滤波器的基础上，每个通道输出开关处再额外引出2个相邻的时钟开关，具体电路如图3所示，相邻开关相位相差45°，当输入信号从fs变为3fs或5fs时，采样向量之间的相位差从45°增加到3×45°、5×45°。图4(a)、图4(b)和图4(c)分别是输入频率为fs、3fs和5fs时系统的输出相量图。为了消去3fs和5fs处的谐波，如图4(d)所示，通过将所有向量之和乘以适当的比例因子bk，使3个向量和为零。此时电路传递函数可以改写成

图3 采样电路

图4 向量计算

(10)

对于8通道滤波器，要衰减3、5次谐波，必须满足以下联立方程:

(11)

(12)

在此电路中，射频信号首先由混频开关下变频，混频开关由非重叠连续时钟驱动，然后，经过电容滤波后传输到3个驱动时钟具有偏差的混频开关中，将信号上变频到所需频率，并通过跨导放大器以一定比例进行加权求和，实现特定频率谐波的抑制。

2.2 谐波折返消除

从式(6)可以看出，N通道滤波器不仅表现出多次谐波的特性，而且对于所需的f=fs处通频带，所有可能的(n+m=kN)值都可能出现折返现象，即所有(kN±1)fs左右的输入频率都将“折回”到频率fs。对于8通道滤波器来说，混叠到中心频率fs处的最强谐波出现在(N±1)倍的中心频率处，即7次和9次谐波[27]。因此本文设计主要目的是消除出现在(N±1)×fs处的最强折返效应。

降低HFB的一个方法是使用具有良好选择性的带通滤波器来衰减出现在(N-1)×fs、(N+1)×fs、(2N-1)×fs、(2N+1)×fs等频率的信号。实现这种滤波器有以下几种选择:有源RC滤波器、Gm-C滤波器和无源滤波器。有源RC滤波器很难或有时不可能在更高的频率上实现。Gm-C滤波器在较高的频率时线性度较差。而无源滤波器需要电感，电感占用芯片面积大，且滤波器通常品质因数低，不能作为高选择性带通滤波器使用。

由于折返效应都是由于信号传输时上变频采样和下变频采样引起的，因此本文采用信号叠加的方式来同时降低HFB。如图5所示，2个相同的N通道滤波器输入输出端相连，滤波器1、2电路使用前一部分介绍的电路结构，不同之处在于所有路径的输入和输出开关都由具有相同频率但不同相位的8路非重叠时钟控制[28]。时钟频率保持不变，因此不需要更快的开关，也可以防止更高的功耗。

图5 2×N通道滤波器结构框架

假设2个N通道滤波器之间时钟信号偏移为Δt，那么2个滤波器频率偏移exp(-j(m+n)wsΔt)。以N通道滤波器1为基准，其传递函数为式(10)，那么滤波器2的传递函数F2(w)为

F2(w)=exp(-j(m+n)wsΔt)F(w)。

(13)

2个滤波器连接到同一输出端，改进后的N通道电路传递函数为

F2×N(w)=[1+exp(-j(m+n)wsΔt)]F(w)。

(14)

若要消除在(N±1)×fs处的折返效应，即输入为Vin(w-Nws)时，输出F2×N(w)为0。此时有:

1+exp(-j(m+n)wsΔt)=0,m+n=N。

(15)

(16)

式(16)表明，如果CLK2与CLK1相比具有Ts/2N(k=0)时移，则从|N±1|fs到fs的HFB将被移除。

3 电路实现

本文所采用的N通道滤波器由开关电容电路、跨导放大器和时钟发生器等结构组成，原理如图6所示。差分结构用于抑制偶次谐波，2个相位相差180°的通道合在一起，分别连接到一个电容的正负两端，有效减小了芯片面积，此时，电路共需要8个电容，相比于之前减少了一半。实际电路中，电容使用MIM电容，开关使用单个MOS管代替。为了有效减少它们的噪声、非线性以及电路失配，选择低导通电阻开关，其宽长比(W/L)为260 u/1u，MOS管导通电阻Rsw为10 Ω。在任意时刻，滤波器1与滤波器2各有一条通路导通，两路滤波器的电容之间将存在电荷共享，通带损耗增加。因此，在滤波器的输入端添加一个电阻R，以防止电荷共享。如果电阻(Rsw，R)的总阻抗比电容的总阻抗大得多，则电荷共享将减少。为了对多次谐波以及折返效应进行抑制，本文对传统滤波器结构进行改进，电路输入输出阻抗变化，因此，在电路两端加入阻抗匹配模块，以减少回波损耗。

图6 滤波器原理

跨导Gm用作电压-电流转换器。其中每个基带电压被相应的跨导放大器转换为电流，电流经过输出电阻RL，产生输出电压Vout。图7展示了一个全差分的运放，它是一个具有可调电流源和相对较大电阻的自偏置共栅放大器。连接到MOS管源极的4个大电阻用作源极负反馈电阻以获得高输出电阻，因此可通过调节尾电流的大小来调节Gm值。根据Cadence仿真结果，将Gm级的电流调整为0.5～3.0 mA，在此范围内，有效Gm可在2.5 ms到10.0 ms之间变化。

图7 全差分Gm电路

图8展示了占空比为1/8的八相时钟发生器。输入系统时钟CLK来自芯片外，比开关频率fs快8倍，可由片外振荡器提供。D触发器用于时钟生成电路，包含2个互补开关和2个反相器。4个边沿触发的D触发器，每个触发器的输出端接到下一个触发器的输入端。因为信号在触发器间传递需要时间，而时钟信号的更新只在上升沿加到触发器上时，所以当时钟信号同时加到4个触发器上时，每个触发器接收的都是上一个D触发器中原来的数据，2个寄存器输出信号时间偏移为时钟CLK的周期。因为电路中反相器的存在，信号在高低电平间变换。

图8 时钟产生电路

将其中2个输出通过与门可产生占空比为1/8的时钟，用于产生时钟信号。CLK1与CLK相同，CLK2与CLK1之间存在Ts/16的时移，从时序图中可以看出，时移后CLK2可视为是CLK1的倒置。CLK1和CLK2通过8个级联D触发器组成的移位寄存器，每经过一个D触发器，时钟向后移动Ts/8,以产生控制时钟S11到S18和S21到S28。

4 电路仿真结果

图9 电路版

图10 开关频率可调范围

图11 S11模拟结果

图12 fs=500 MHz时的S21

图13 不同频率下的噪声系数(NF)

图14 最强折返谐波

最后，本文设计的滤波器与其他文献设计的性能比较如表1所示。文献[20]结构衰减了谐波折返，但未对多次谐波进行分析，功耗较高；文献[21]滤波器实现对偶次谐波的抑制，且功耗较低，但电路中的奇次谐波仍然存在，同时，该电路IIP3较差，线性度有所不足；文献[22,24]主要抑制电路奇次谐波，且都获得了较好的效果，但谐波折返未进行衰减，仍有其他频率输入信号叠加至所需信号；文献[23]采用LC结构对电路进行预滤波，实现了对谐波的抑制，但由于使用了电感，版图设计时面积将大大增加。经文献对比说明本文使用的HS-HFB结构，在其他性能指标相似的情况下，较好实现了3次和5次谐波抑制和折返消除，具有更好的滤波特性。然而，2个滤波器叠加的结构使电路功耗增加，在今后研究中可考虑对电路中的跨导放大器进行优化，使其能在更小的电流下运行电路。

表1 性能对照

5 结论

本文介绍一种具有谐波抑制和降低谐波折返效应的N通道滤波器。利用傅里叶级数展开，导出N通道滤波器的传递函数，包括谐波抑制电路和HFB电路结构的传递函数。通过N通道采样差分结构，在抑制多余谐波的前提下，有效地减少了折返效应，特别是位于(N±1)×fs的最强折返。仿真结果表明，滤波器可实现0.3～1.0 GHz的调谐范围，3fs处谐波抑制达到了49 dB,HFB中H8(f)可降低51.8 dB。与其他结构相比，该结构在同时考虑HS和HFB降低的情况下，获得了更好的滤波特性。该滤波器具有可调性好、谐波抑制效果好等优点，可用于接收机前端系统，并可用于其他N通道滤波器的设计。