不同应变率下聚甲醛纤维机场道面混凝土弯曲性能研究
2022-08-08王祯辉郭荣鑫张久长李黎山
王祯辉,郭荣鑫,晏 永,张久长,李黎山
(1.昆明理工大学建筑工程学院,云南省土木工程防灾重点实验室,昆明 650500; 2.昆明理工大学云南工业干部学院,昆明 650500)
0 引 言
机场混凝土道面供飞机滑行、起飞和降落使用,道面结构在服役过程中需要承受各种复杂环境作用、弯拉疲劳荷载及冲击荷载的反复作用,不同性质荷载及冲击作用下道面混凝土应变率不同。混凝土承受不同性质荷载时,材料随之反馈出不同量级的应变[1],准静态荷载应变率变化范围为10-6~10-5s-1,车辆冲击荷载应变率变化范围为10-4~10-3s-1,飞机冲击荷载应变率变化范围为10-2~10-1s-1,强烈冲击荷载应变率变化范围为100~103s-1。混凝土是应变率敏感材料,其强度、韧性等均会随应变率不同而变化。
纤维混凝土动力性能的研究对其用于机场道面建设有着重要的意义,在当前混凝土动态力学性能试验中,以分离式霍普金森压杆(split Hopkinson pressure bar, SHPB)试验系统及液压试验系统较多。SHPB技术被认为是测量固体材料在高应变率(101~103s-1)下动态特性的最有效的方法[2]。Wang等[3]通过材料测试系统和SHPB试验研究了钢纤维混凝土的压缩力学行为,发现素混凝土在低应变率的单一冲击下可能会失效,而纤维混凝土可以抵抗高应变率的重复冲击,应变率对混凝土强度影响较大。肖岩等[4]基于SHPB技术对轻质高强纤维混凝土进行冲击试验研究,发现应变率在40~140 s-1时,混凝土动态强度随着应变率的增大而增大。相较于SHPB系统,液压试验系统技术相对成熟,应变率/荷载速率控制精度高,测量精确且方便,该类设备适用于10-5~10-1s-1应变率范围下各种不同性质荷载对混凝土性能影响的研究[2]。部分学者基于液压试验系统对不同应变率下各种水泥基材料开展了研究。宣卫红等[5]对高性能水泥基复合材料(high performance cement-based composites, HPCC)在不同应变率下的断裂性能进行了研究,发现HPCC弯曲强度与应变率比呈对数关系,含钢纤维HPCC断裂能对应变率敏感性略低于HPCC。周知等[6]研究发现,钢纤维橡胶混凝土的动态抗压强度随应变率的提高而增大。Millard等[7]研究发现,超高性能纤维增强混凝土的弯曲强度随应变率的增加而降低,且高强混凝土具有较低的应变率敏感性。
聚甲醛(polyoxymethylene, POM)纤维是一种具有良好力学强度、耐碱腐蚀性及高硬挺度的新型有机纤维,根据本课题组相关研究成果,POM纤维在机场道面混凝土中具有明确的应用价值,而关于POM纤维机场道面混凝土(POM fiber airport pavement concrete, PFAPC)动态力学性能的研究较少,对其开展动态力学性能研究具有重要意义。SHPB系统由于测试应变率(101~103s-1)较高,对机场道面混凝土而言,其承受飞机冲击荷载时应变率变化范围为10-2~10-1s-1,SHPB试验对低应变率工况有一定局限性,因此本研究基于液压试验系统开展。本文考虑了五种加载应变率,对PFAPC进行了四点弯曲试验,分析了其抗弯挠度、弯曲模量、弯曲强度、韧性指数等参数随应变率变化的规律,通过观察POM纤维断口形貌,总结了各应变率下的纤维失效模式。
1 实 验
1.1 原材料及配合比
PFAPC的性能见表1。水泥采用P·O 42.5水泥,其密度为3 100 kg/m3。粉煤灰采用F型Ⅰ级低钙粉煤灰,其密度为2 300 kg/m3。矿渣粉采用S95级高炉矿渣粉,其密度为2 900 kg/m3。粗集料采用4.75~16.00 mm和16.00~26.50 mm双级配碎石,其合成表观密度为2 748 kg/m3。细集料依据昆明地材特点选用机制砂,规格为Ⅰ区粗砂,细度模数为3.13,表观密度为2 708 kg/m3。水采用当地生活饮用水,外加剂采用聚羧酸高性能减水剂。POM纤维产自云天化集团有限责任公司,其物理力学指标见表2。

表1 PFAPC的性能Table 1 Properties of PFAPC

表2 POM纤维的物理力学指标Table 2 Physical and mechanical indexes of POM fiber
1.2 试件制备及试验方法
为充分考虑试件的质量及均匀性,严格控制各组分投料顺序以及搅拌时间。先将胶凝材料与粗、细集料混合干拌1 min,再将纤维均匀撒入混合料中继续干拌1 min,最后将混合均匀的水/减水剂溶液加入拌合物中继续搅拌直至纤维分散均匀。将拌合物装入100 mm×100 mm×400 mm试模,振捣密实后待24 h脱模,放入温度(20±2) ℃、相对湿度95%以上的标准养护室养护至28 d后进行四点弯曲测试。
从养护室取出试件后用打磨机对其受压面及底面进行抛光处理并在底面粘贴应变片,采用四点加载方式,使用CSS-44100电子万能试验机按位移控制加载,位移加载速率分别为0.04 mm/min、0.43 mm/min、4.31 mm/min、43.13 mm/min和431.25 mm/min,相应的应变率分别为10-5s-1、10-4s-1、10-3s-1、10-2s-1和10-1s-1。在试件跨中位置设置位移传感器,在加载过程中同步采集加载荷载、跨中梁底轴向拉伸应变以及跨中挠度等数据。加载示意图如图1所示。四点弯曲试验结束后,对试件断口处进行切割,切割成边长约25 mm的含纤维立方体,使用带图像采集系统的德国ZEISS Axio Imager Vario光学显微镜观察其微观形貌。

图1 加载示意图Fig.1 Load diagram
2 结果与讨论
2.1 弯曲性能
采用弯曲强度(峰值强度及残余强度)、抗弯挠度(极限抗弯挠度及峰值挠度)、弯曲模量等指标来表征PFAPC弯曲性能,其中以断裂后的最大强度(第二峰值强度)作为其残余强度。不同应变率下PFAPC弯曲荷载-挠度曲线如图2(a)所示,不同应变率下PFAPC弯曲应力-应变曲线如图2(b)所示,PFAPC在不同应变率下的弯曲强度及弯曲模量变化如图3所示。PFAPC在不同应变率下的挠度及弯曲模量等结果详见表3,每个值为三组数的平均值。
对于弯曲强度,结合图3和表3可以看出,应变率从10-5s-1升至10-2s-1,PFAPC峰值强度总体呈上升趋势。其中以应变率10-5s-1及10-4s-1加载时,PFAPC峰值强度变化不明显,在10-2s-1应变率作用下PFAPC峰值强度及残余强度最高。一般认为,在冲击荷载作用下,水泥基体内部缺陷发生的时间较短,根据运动能量冲量规律,冲击时间随冲击速度的增大而减小,断裂起始会吸收更多的能量,在短时间内使弯曲应力增加[8]。当应变率由10-2s-1增加至10-1s-1时,PFAPC峰值强度出现异常下降情况。通过查阅文献[9]发现在10-5~10-2s-1应变率范围内,混凝土基体梁及超高韧性水泥基复合材料梁的弯曲峰值强度随应变率的变化均不成规律,但总体呈上升趋势,这与本试验结果相符。与10-5s-1应变率下的峰值强度及残余强度相比,其他应变率下PFAPC峰值强度变化范围为-10.9%~33.5%,残余强度变化范围为5.5%~25.0%,相比峰值强度,应变率对残余强度影响较小,但随应变率增大总体呈上升趋势。
对于弯曲模量,从表3可看出,应变率从10-5s-1增加到10-1s-1,PFAPC弯曲模量呈上升趋势,提升了11.54%。从图2(b)可看出,在不同应变率作用下,PFAPC最大应变变化不显著,动荷载作用下的弯曲应力随着弯曲应变的增加而近似呈线性增加,曲线的总体变化趋势并没有随应变率的增加而发生显著变化,这也就导致了PFAPC弯曲模量并没有随应变率数量级的增加而显著增长。
对于抗弯挠度,从图2(a)及表3可看出,随着应变率的增加,与10-5s-1应变率下的峰值挠度及极限抗弯挠度相比,其他应变率下PFAPC峰值挠度变化范围为7.1%~28.7%,极限抗弯挠度变化范围为15.8%~64.2%,相较于极限抗弯挠度,峰值挠度随应变率的增加而波动上升,即认为应变率对PFAPC开裂前阶段的影响较小,而极限抗弯挠度则随应变率的增加而呈增大的趋势,即认为应变率对开裂后阶段的荷载-挠度曲线影响较大。PFAPC荷载-挠度曲线在试件加载初始阶段呈线性上升趋势,达到峰值荷载后平缓下降,随着应变率的增加,曲线更饱满且面积增大,而且在各应变率下,曲线均出现二次强化,荷载明显出现二次峰值,这与POM纤维在基体断裂过程中能够有效桥接并吸收大量能量有关,在试件开裂后,纤维能够继续承受一定量荷载,使PFAPC试件在各应变率作用下均能表现出良好的塑性变形能力及延性。
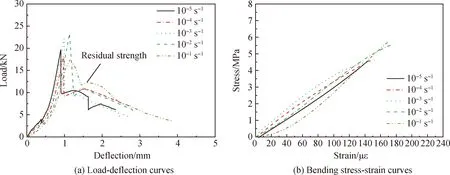
图2 不同应变率下PFAPC的弯曲性能Fig.2 Bending properties of PFAPC under different strain rates
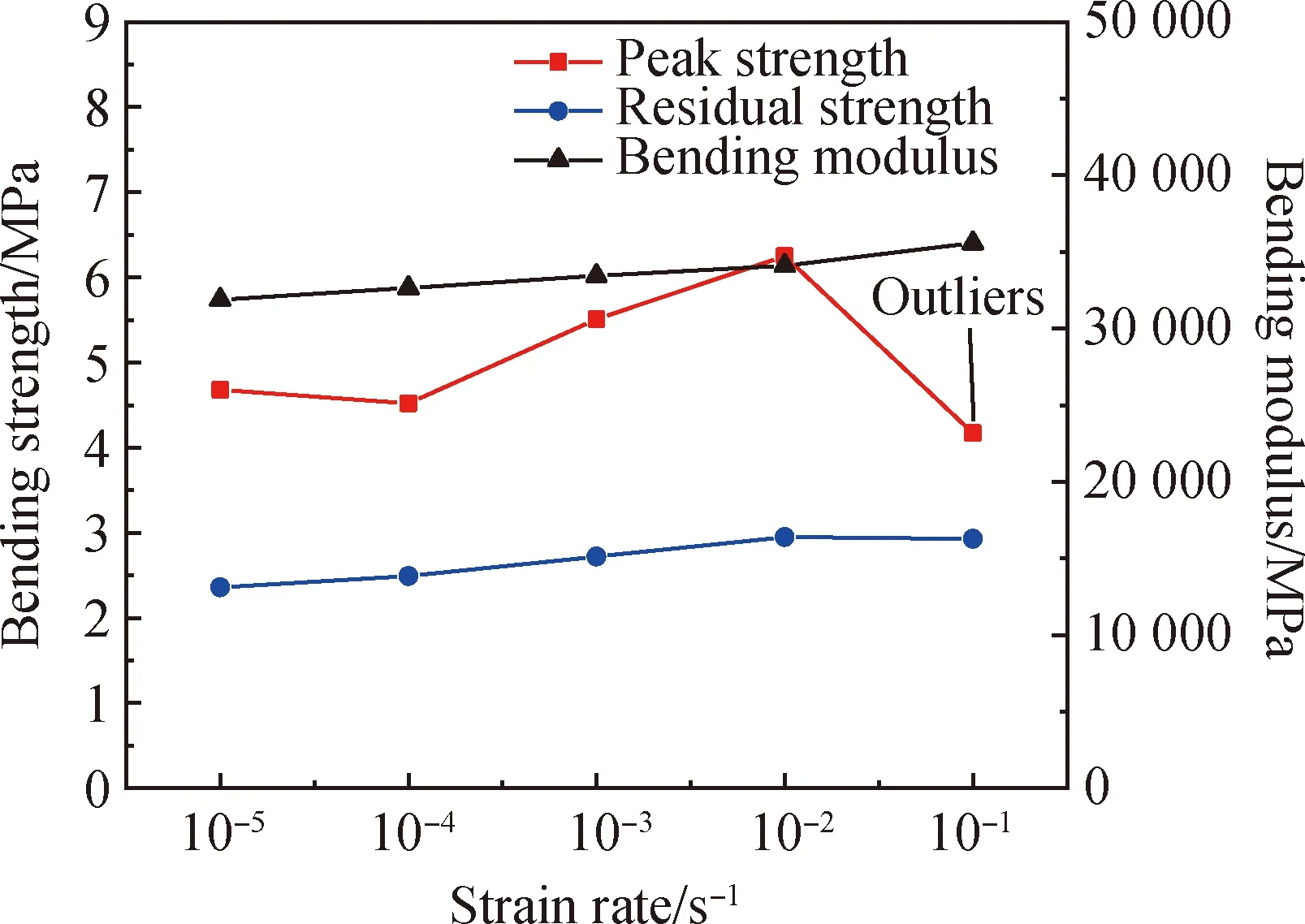
图3 不同应变率下试件的弯曲强度及弯曲模量Fig.3 Bending strength and bending modulus of specimens under different strain rates

表3 不同应变率下试件弯曲性能Table 3 Bending properties of specimens under different strain rates
2.2 POM纤维断裂形貌
不同应变率下PFAPC试件中POM纤维断裂形貌如图4所示。从图4(a)~(c)可看出,在准静态(10-5s-1)及车辆冲击荷载(10-4~10-3s-1)作用下,由于加载速率相对较低,PFAPC基体裂纹扩展也较缓慢,POM纤维直接从基体中拔出,其整体形貌较为完整;当考虑到飞机冲击作用(10-2~10-1s-1)时,纤维虽能从基体中完整拔出,但其表面有不同程度的基体碎屑黏附,见图4(d),极少数纤维出现断裂破坏现象,如图4(e)所示。在五种应变率作用下,POM纤维的拔出是主要的失效模式,颈缩及拔断破坏较少。

图4 不同应变率下PFAPC中纤维断裂形貌Fig.4 Fracture morphology of fibers in PFAPC under different strain rates
2.3 弯曲韧性指数
韧性是评估材料和结构在地震、冲击和爆炸荷载下能量吸收能力的一个有效参数[10]。弯曲韧性用来考察纤维混凝土开裂后的增韧效果,一般用纤维混凝土在弯曲破坏过程中吸收的能量来进行计算和评价[11],弯曲韧性定义为在荷载-挠度曲线下达到一定挠度的面积。关于PFAPC的弯曲韧性,利用当前国际上较为流行的ASTM C 1018标准[12]进行评定。ASTM C 1018 标准评价方法采用弯曲韧性指数I(I5、I10、I20)及残余强度系数R(R5,10、R10,20)来表征纤维混凝土的弯曲韧性。I5、I10、I20及R5,10、R10,20的计算公式分别为:
(1)
(2)
式中:δ为初裂点对应的跨中挠度,mm;Tδ、T3.0δ、T5.5δ和T10.5δ分别为初裂挠度δ、3.0δ、5.5δ和10.5δ时荷载-挠度曲线下的面积,kN·mm,即图5(a)中OAB、OACD、OAEF和OAGH所包围的面积。初裂点为荷载-挠度曲线上升段首次出现由线性变为非线性的转折点,详见图5(a)中的标注,P为初裂点对应的起裂荷载。ASTM C 1018标准规定,对于理想弹塑性材料,其荷载-挠度曲线如图5(b)所示,I5=5,I10=10,I20=20,R5,10=100,R10,20=100,低于该值则说明材料具有相对较低的塑性,对于素混凝土,R趋于0。
根据ASTM C 1018标准计算得到不同应变率下PFAPC的韧性指数和残余强度系数,如表4所示。理论上讲,PFAPC的弯曲韧性指数应小于理想弹塑性材料,但从表4可看出,当应变速率为10-3s-1、10-2s-1和10-1s-1时,PFAPC的I5、I10、I20值出现大于5、10、20的现象。文献[13]参照ASTM C 1018标准计算得到的韧性指数,除个别情况外,均大于理想弹塑性材料的相应值,并认为这主要与纤维混凝土受力特点以及弯曲初裂点的选取方法有关。文献[14]对通过ASTM C 1018标准计算出的弯曲韧性指数结果偏大同样提出了质疑,并认为对于理想弹塑性材料,超过初裂点后荷载不再增长,而纤维混凝土有较高的残余弯曲强度,这就导致弯曲韧性指数计算结果偏大。对于本试验,在10-5s-1和10-4s-1两种应变率下,PFAPC韧性指数值均小于理想弹塑性材料。随加载应变率的升高,PFAPC韧性指数有较大的增长趋势,特别是在飞机冲击荷载(10-2~10-1s-1)工况下,其弯曲韧性指数增幅较大,这表明PFAPC在冲击荷载作用下能吸收较大的能量,产生一定变形而不被破坏,具有一定的弯曲韧性。同样,这也解释了为何当应变率为10-2s-1和10-1s-1时,PFAPC抗弯挠度有所增长(见表3),文献[15]也得到类似的结论。此外,从表4中可看出,PFAPC的残余强度系数稳定在100左右,则认为该材料具有优良的韧性。
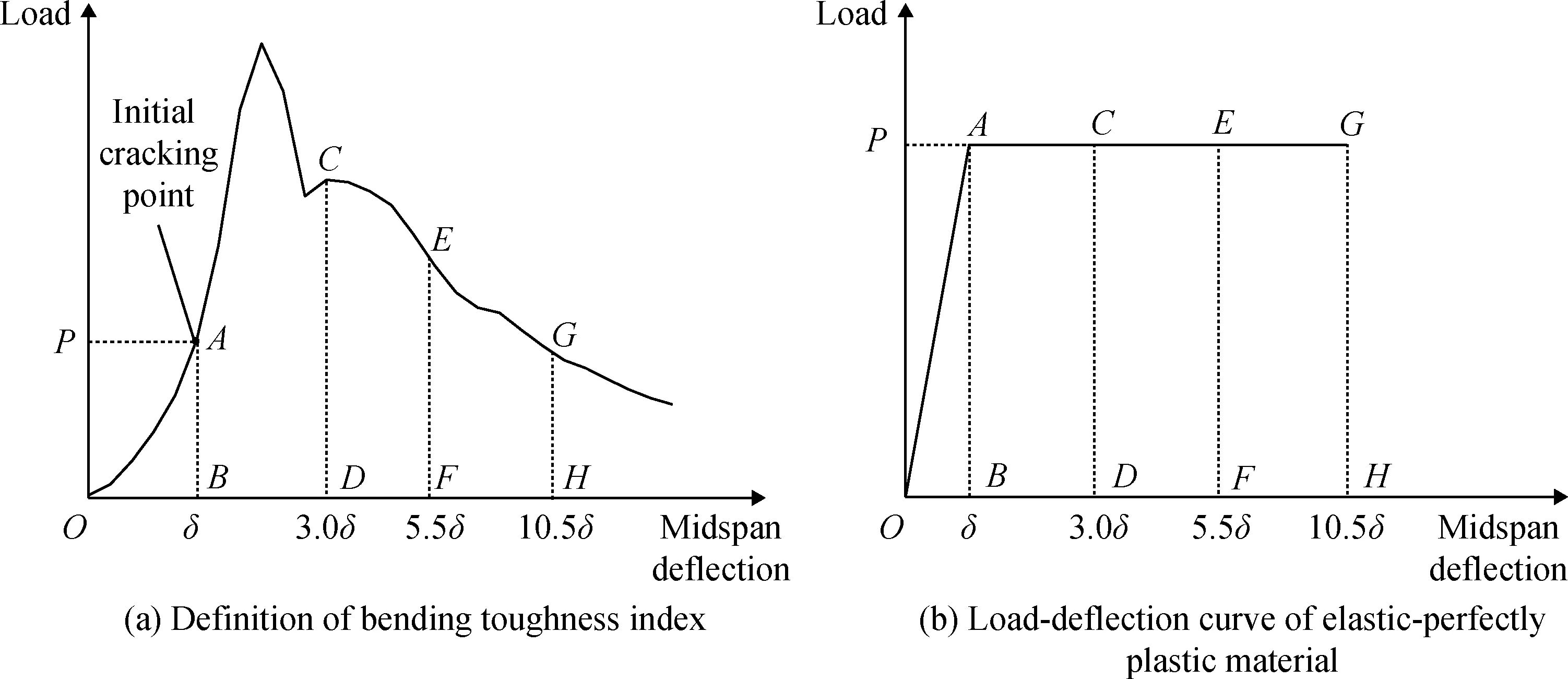
图5 弯曲韧性指数计算示意图Fig.5 Calculation diagram of bending toughness index

表4 不同应变率下的韧性指数I和残余强度系数RTable 4 Toughness index I and residual strength coefficient R under different strain rates
3 结 论
(1)PFAPC的弯曲峰值强度随应变率增大总体呈上升趋势,其中在10-1s-1应变率下,出现异常下降。相比峰值强度,应变率对残余强度影响较小但随应变率增大总体呈上升趋势。随着应变率增大,PFAPC弯曲模量有增加的趋势。相较于极限抗弯挠度,峰值挠度随应变率的增加波动上升,即对开裂前阶段荷载-挠度曲线影响较小,而极限抗弯挠度则随应变率的增加呈增大的趋势,即对开裂后阶段荷载-挠度曲线影响较大。
(2)在各应变率作用下,POM纤维破坏模式主要为拔出破坏。
(3)PFAPC能在车辆及飞机冲击作用下吸收大量能量,产生一定的变形而不被破坏,具有优良的弯曲韧性。
