一种基于混沌加密算法的差分跳频方案设计

尹爱兵,李 毅

(安徽文达信息工程学院，合肥 231201)

0 引 言

短波通信通过电离层反射到达接收端，是军事通信中远距离通信的重要手段。随着军事通信与对抗技术的不断发展和进步，短波通信迫切需要解决高速数据传输与抗跟踪和抗跟踪干扰问题。美国Sanders公司研制的关联跳频扩谱(Correlated Hopping Enhanced Spread Spectrum, CHESS)短波电台采用差分跳频体制，跳速高达5 000跳/s，最大传输速率可达19.2 kbit/s，是短波高速数据通信的一个重要发展方向。差分跳频是一种新的跳频技术，集跳频图案、信息调制与解调于一体，其中 G函数算法是差分跳频的核心技术之一。文献[1-2]提出了同余理论的G函数算法，该G函数实现简单，具有良好的一维均匀性，但二维连续性和随机性较差，很容易被破译。本文在讨论差分跳频G函数基本原理的基础上，分析了常规同余算法生成的G函数的缺点，设计了一种logistic混沌函数生成长周期伪随机序列对跳变频率进行加密的方案，并对加密后G函数的随机性和均匀性进行了讨论，比较了加密前后系统的性能。

1 差分跳频基本原理

普通跳频的频率跳变由伪随机码控制，收发双方在严格同步的基础上进行解跳，而差分跳频的频率跳变由前一跳频率和输入信息符号确定[3]，其数学表达式为

式中：G()为特定的函数，由其决定差分跳频的算法；fn为第n时刻差分跳频的频率，fn-1为当前n时刻前一次差分跳频的频率；xn为当前n时刻差分跳频携带的信息数据。相邻频率之间的相关性携带了发送的信息数据，每跳信息数据最大可达4 bit，传送速率可根据实际环境灵活调整。

要恢复原发送数据，在接收端对发送信号进行宽带接收，对跳频范围内的射频信号进行快速傅里叶变换(Fast Fourier Transform, FFT)分析，检测每跳对应的频率，由G函数的逆变换恢复出携带的数据信息[4]，即

式中，G-1()为G()的逆映射。G函数决定了差分跳频系统的性能，决定着系统接收与抗干扰的性能。

差分跳频G函数可看成是一个频率转移函数，可以用有向图表示，跳频集中，每个频点代表有向图的节点，每跳传输的比特决定频率转移路径。图1所示为64个频点组成的频率转移图，图中每个节点表示频率集中的某一频率点，从一个频点转移到另一个频点用箭头来表示，箭头上为发送的数据。由于每跳传递2 bit数据，因此有00、01、10和11共4种情况，根据传递的数据从当前频率转移到下一频率。由于每次传递2 bit数据，因此只有4种跳变路径，从当前频率只能转移到固定的4个频率之一，有限个频率转移路径很容易被敌方干扰与侦获。差分跳频的接收，可以根据前后频率之间转移关系恢复发送的数据。

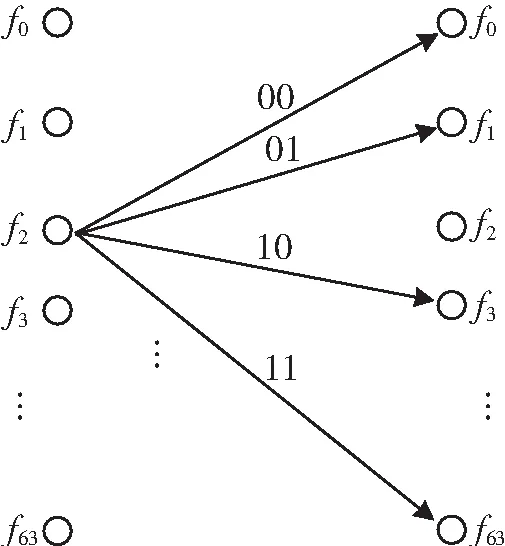
图1 64个频点频率转移图

2 G函数跳变频率混沌映射方案

假设某差分跳频系统的频率集为{f|f0，f1，…，fM-1}，M为频率集中频点个数；每跳传输的信息比特长度为HBP, 信息符号对应的集合为{Xn|0,1,…,2HBP-1}。

文献[1]给出了同余常规G函数算法：

式中，a和b为互质整数。该跳频图案一维均匀性好，但二维均匀性较差，主要是扇出系数较少，很难随机转移到每个频点。为增加扇出系数，增加输入信息序列长度，将跳频等概地转移到各频点，也可以对生成的跳频频率进行随机扰动，映射到每个频率点。

由于跳频频率为频率集中的某一个频点，采用随机扰动方法将频点进行加密，其实现方案如图2所示。由图可知，在常规G函数基础上对跳变频率进行扰动，将前后相关的差分跳频频点扰乱为随机序列，切割前后频点之间的关系，提高差分跳频序列的保密能力，其性能的好坏与采用的混沌序列有关。加密算法主要与随机跳变频率序号有关，与具体频率没有关系，每跳加密时从伪随机序列中取N序列长度作为扰动序列，与每跳频点序号进行运算，生成新的频点序号。假设频率集中频点个数为2N，随机二进制序列为N位，最简单的扰乱即将两二进制序列进行模N加运算，可得到新的混沌序列。

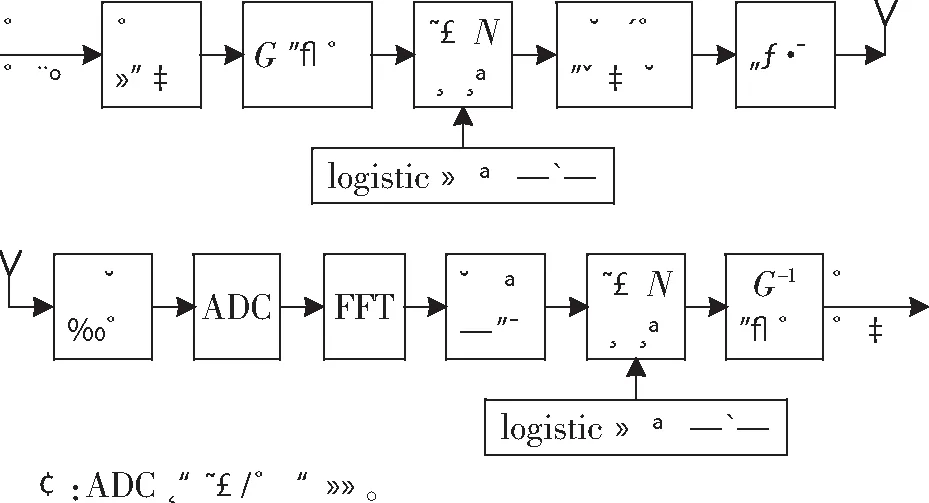
图2 差分跳频G函数加密通信系统

在接收端，对接收的射频信号进行ADC，再进行FFT运算，剔除无关频点，只对频率集对应频点进行检测，解跳出每个跳频频率对应的频率集序号，再对频点序号进行解密，恢复G函数产生的频点序号，然后利用前后频点之间的相关性恢复发送数据[5]。在解跳中，由于是按照每跳进行加密解密，因此，加密后的差分跳频通信系统需要跳同步，在跳同步的基础上接收端采用与发送端相同的伪随机序列进行解密，否则无法恢复出发送数据。

3 logistic 混沌序列的数字实现

混沌信号随机性好，类似于通信中的噪声，并且对初始值比较敏感，是当前研究伪随机序列的一种新的实现方法。logistic方程为典型的混沌系统，易于实现，其数学表达式为

式中，μ为系统参数。logistic映射的动态行为与参数μ有关，随着参数μ取值不同，表现出周期性或混沌。当3.569 99<μ≤4.000 00、xn初值取0～1之间任一数值时，经多次迭代后，取值进入混沌状态，否则会表现出周期性。

logistic方程每次迭代得到的是混沌随机数，结果为(0,1)之间的任意值。要得到随机数字序列，需要对logistic方程进行数字化，对方程中的数值采用多位二进制量化。

首先对μ值进行量化，由于μ为(3，4)之间的数值，故对式(4)做如下变换：

式中，d取值区间为(0，1)。可以进行小数量化，连续的实数μ被量化为有限长的数字序列进行运算。

在logistic混沌离散化实现过程中，由于数字信号处理器件的有效字长效应，系统性能会使混沌序列出现短周期现象，导致混沌序列安全性降低。

对于混沌序列的周期性，可以通过自相关进行检测[6]。假设x(n)为混沌二进制序列，其自相关函数Rx(m)可定义为

图3以32 bit logistic 随机序列发生器为例，仿真对比了32 bit量化logistic序列长度的周期性。图3(a)所示为式(5)中参数取值进行32 bit量化后多次迭代产生序列长度为800 000的自相关性能。如图所示，图中出现了明显的周期谱线，说明量化后的混沌序列存在短周期现象。为提高混沌序列长度，可以采用增加量化长度或采用M序列进行扰动。图3(b)所示为对迭代次数每隔4 096进行6 bit随机加扰后的自相关函数，如图所示，只有一条明显的谱线，与理想的伪随机序列自相关特性类似。对比加扰前后自相关函数可知，通过加扰可以得到更长周期混沌序列。

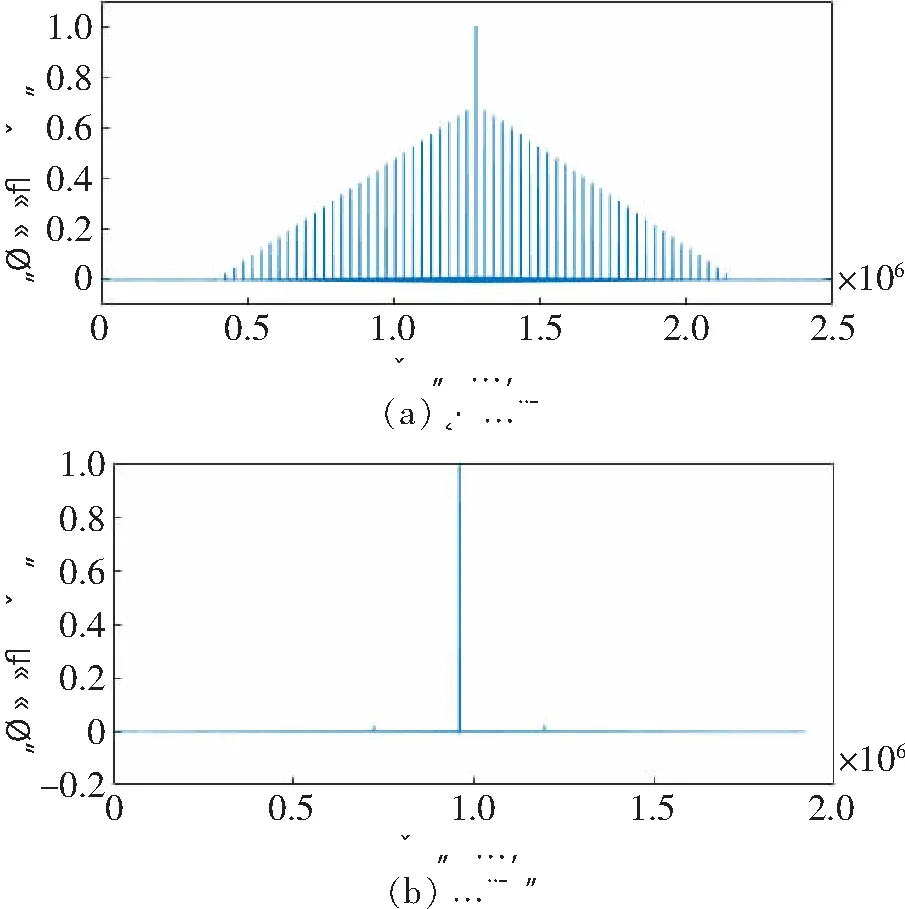
图3 32 bit混沌序列自相关函数

4 G函数性能校验

短波差分跳频信号是一种重要的军事通信手段，需要防止对方干扰与截获破译，因此，跳频码频率跳变要有良好的随机性，防止敌方利用相关性进行破译。为提高抗阻塞干扰能力，要求发射的频率在跳频带宽内随机均匀分布，可对其均匀性、随机性和系统误符号率进行检验[7]。

4.1 均匀性分析

跳频码的均匀性分为一维和二维均匀性。一维均匀性即某一段时间内每个频点出现的次数基本一致。对于N个频点的差分跳频集，每个频点出现的概率相同，为1/N。二维均匀性表示在当前频率情况下转移到下一个频点的概率，从抗侦察角度来说，应该等概跳变到每个频点，其校验可以由第i个频点后出现第j个频点的概率来求得。

表1为对本文G函数进行均匀性校验的数据，校验采用随机分布的二进制数据，0、1等概分布，初始频点为频率集中任意点，对一维和二维均匀性校验采用数理统计中的χ2检验，假设频点q=64,跳频长度L=16 384，信息符号为随机序列，取50组进行校验。根据文献[1]分析，对于指定显著性水平α=0.05情况下，χ2理论值为82.2，由表1仿真结果可知，不论混沌序列量化为16位或32位，检测数据计算值都小于理论值，混沌映射后的差分跳频码具有较好的一维均匀性。二维均匀性校验中，χ2理论值为4 244.7，当logistic量化为32 bit时，产生的混沌序列扰乱可以满足要求；当量化为16 bit时，量化后的混沌序列扰乱的二维均匀性超过理论值，不满足要求。因此，要产生满足要求的差分跳频码，logistic混沌序列必须采用32 bit量化。

表1 一维与二维均匀性校验

4.2 跳频码功率谱

跳频信号为典型的随机信号，可以防止对方的侦察和干扰，自相关函数或功率谱密度能直观地反映信号之间的相关性。自相关函数求解较复杂，采用功率谱估计更方便，目前求解方法较多，有周期图法、Welch法和短时傅里叶变换等，一般采用平滑周期图平均进行估计。

本文直接调用Matlab软件中的welch功率谱估计函数pwelch()对采用常规G函数与加密后的G函数进行功率谱估计。假设跳频频点为64个，一跳传递2 bit数据，图4所示为两种跳频码归一化功率谱，横坐标为频率，纵坐标为功率；图4(a)所示为常规G函数产生的跳频码功率谱，频谱集中在低频端，随机性差；图4(b)所示为常规G函数跳频码加密后的功率谱，功率分布于各频率上，频谱相对平坦，随机性好。对比加密前后频谱可知，常规G函数生成的频点相关性强、变化慢和抗窄带干扰能力弱，而加密后的频点在全频段随机变化，具有较强的抗干扰能力。

图4 G函数功率谱

4.3 误符号性能分析

由图1可知，从接收端来看，差分跳频通信系统可看成多进制频移键控(Multi Frequency Shift Keying，MFSK)调制，接收端在宽带接收中从M个频点中选择发送的频率。同余差分跳频从某一个频点出发只能转移到4个固定的频点，接收端在解跳前一频率基础上根据同余算法可推测出下一跳的4个转移频点，只要从4个频点中选择一个即可，可等效为4进制频移键控(4 Frequency Shift Keying, 4FSK)调制。本文在同余算法基础上，通过加扰改善二维均匀性时，每个频点都可以随机跳变到频率集中任一个频点上，从接收解调来看，可以等效为NFSK调制(N为频率点数目)。根据通信系统性能分析可知，在同样的通信条件下，由于同余差分跳频可以利用冗余频点减少频点检测的差错率，其性能要好于本方案。

为比较加密后系统性能，根据图2对差分跳频系统进行建模。假设差分跳频频率集为64个频点，每跳传递2 bit数据，信道为理想情况(假设为高斯白噪声信道)，每个频点间隔10 kHz，在2.56 MHz带宽内随机选择64个频点，接收机采用宽带接收，采样后的信号是跳频信号与宽带噪声的混合信号，在一跳周期内采样1 024点，对采样的信号做1 024点 FFT分析，分析各频点落入512个FFT频点上的信号大小。在FFT频点上采用能量比较检测法，检测出频点在频率集中的序号。图5仿真了64个频点在高斯白噪声信道下，采用FFT进行解调的系统性能，本方案在64个频点上进行检测，同余算法利用与前一频点相关性在4个频点进行检测，由仿真结果可知，利用相关性在有限个频点进行检测，在同样信噪比情况下，误符号率较低，而在全频点进行检测，受干扰点较多，被干扰的概率大，系统性能较差。

图5 差分跳频FFT检测系统性能

5 结束语

本文对常规同余G函数生成的频点序号采用logistic混沌映射产生的伪随机序列进行了加密扰乱，加密去除了前后频点之间的相关性，仿真分析了加密前后的随机性、均匀性与误符号性能，经过加密对有规律的频点进行了随机扰乱，破坏了相关性，提高了二维均匀性与随机性，但解跳无法利用前后相关性，与利用相关性解跳相比，系统性能有所下降，但仍能满足实际需要。