基于人工智能的高铁动车组智能运维数据分析系统的构建

王 平，吴文波，杨友兰，马毅华，许 江，宗智诚

（中国铁路上海局集团有限公司 信息技术所，上海 200071）

近年来，我国高速铁路（简称：高铁）事业飞速发展，高铁动车组列车保有量快速增长，服役车型种类日益增多，高铁产业正由制造为主的阶段转向全寿命周期运营维护（简称：运维）为主的阶段。因此，提高动车组运行的安全性和可靠性，降低运维成本，具有重大意义。

目前，动车组故障预测与健康管理（PHM ，Prognostic and Health Management）系统[1]已在全国铁路投入使用[2]，基于对24种动车组关键部件传感器数据的分析，构建了预警预测、视情维修等故障诊断和预测应用。2021年，动车组PHM系统（由中国铁路上海局集团公司开发的部分）生成故障诊断预警数据近3万条，准确率约为80%，预报了动车组联轴节脱开、轴箱轴承故障、蓄电池烧损等典型故障，有效保障了动车组运行安全；针对动车组的散热装置进行健康度预测，动车组滤棉更换次数、散热装置清洁冲洗次数显著下降，降低了维修成本。

现阶段的动车组PHM系统运维算法模型尚存在如下问题：（1）模型设计依赖于专家经验，具有主观性[3-4]；（2）模型主要基于动车组系统运行机理构建，对较复杂的部件故障难以进行有效预测；（3）利用传统故障诊断方法难以构建动车组部件“健康”与“非健康”的状态分界面，不利于健康管理的深化；（4）利用监督学习构建算法需要高质量的数据标注，但动车组关键部件的故障标注数据尚在积累阶段，健康度标注则还在研究中。

为深化发展高铁动车组智能运维算法，亟需在基于人工智能（AI ，Artificial Intelligence）的高铁动车组智能运维算法研究平台中构建数据分析系统，将AI算法引入特征工程和数据标注环节，利用AI算法打通高铁动车组智能运维算法研究的全过程。

1 系统概述

1.1 平台概述

高铁动车组智能运维算法研究平台包括数据分析系统和建模分析系统，如图1所示。动车组PHM系统将动车组车载信息无线传输系统（WTDS ，Wireless Transmission Device System）数据存入离线数据仓库，作为平台的数据支撑，数据接入平台后，经过数据处理、特征工程、数据标注、模型训练和模型验证等步骤，反复迭代、优化形成稳定可靠的模型，最终部署至动车组PHM系统。

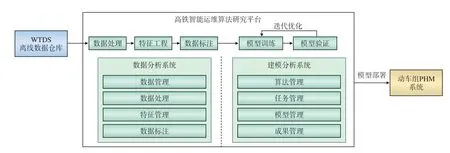
图1 高铁动车组智能运维算法研究平台总体架构

数据分析系统负责进行数据处理、特征工程和数据标注，包括数据管理、数据处理、特征管理和数据标注功能模块；建模分析系统负责进行模型训练和模型验证[5-6]，包括算法管理、任务管理、模型管理和成果管理功能模块。数据分析系统作为建模分析系统的前置环节，可为建模分析系统作好特征工程与数据标注准备。

1.2 数据处理流程

动车组部件的数据海量而繁杂，在现阶段数据标注较为匮乏的情况下，难以进行高效的算法探索与模型分析，针对此问题，数据分析系统设计了具体的处理流程，如图2所示。系统的特征工程部分细分为降维聚类和结果分析2个流程。降维聚类后的结果需经专业人员分析确认后才能作为特征工程环节的输出。数据特征数量较多时，高维度数据样本在空间的分布呈现稀疏性，难以进行进一步分析，在数据处理中被称为“维数灾难”[7]，降维是解决维数灾难的重要方法，降维的目的是在压缩数据的同时让信息损失最小化。在降维的基础上，聚类算法可显著降低数据分析的复杂性，提高聚类结果的可解释性。经“降维—聚类”后的数据可更加直观地反映数据间的潜在关系，有助于后续的数据标注和建模分析。

图2 数据分析系统的处理流程

2 关键算法

2.1 降维算法

2.1.1 主成分分析

主成分分析（PCA ，Principal Component Analysis）是一种经典的线性降维方法[8]。PCA的主要思想是将高维数据通过线性变换投影到低维空间中，并期望在所投影维度上数据的信息量最大（方差最大）。

2.1.2 t-分布随机邻域嵌入

t-分布随机邻域嵌入（t-SNE ，t-distributed Stochastic Neighbor Embedding）是一种非线性降维算法[9]。该算法的基本思想是保持样本点在高维空间和低维空间中的概率分布尽量相似，以达到降维的目的。

2.1.3 均匀流形逼近和投影

均匀流形逼近和投影（UMAP ，Uniform Manifold Approximation and Projection）是一种基于黎曼几何和代数拓扑理论框架构建的非线性流形学习算法[10]。UMAP依据高维空间映射到低维空间相似度的定性结论，将高维数据的拓扑结构进行低维映射以达到降维结果，主要包含构造1个特殊的加权K邻域图和计算该图低维表示2个阶段。

2.2 聚类算法

2.2.1 K-means

K-means算法是一种划分聚类算法。给定一个数据点集合和需要的聚类数目K，该算法根据距离函数反复把数据分入K个聚类中。

2.2.2 Louvain

Louvain算法[11]是一种基于图数据的社区发现算法，优化目标为最大化整个数据的模块度，模块度的计算公式为

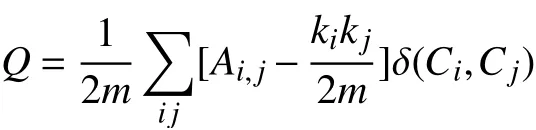
其中，m为图中边的总数量；ki、kj分别表示所有指向节点i、j的连边权重之和；Ai,j表示节点i、j之间的连边权重，Ci表示节点i所属的社区，当Ci=Cj时 ， δ (Ci,Cj)=1，否则 δ (Ci,Cj)=0。 通过Q值可确定社区的分类度，其取值范围为 [0,1]，Q值越大，分类度越好。

2.2.3 变分自编码器

变分自编码器（VAE ，Variational Auto-Encoder）是自编码器（AE，Auto Encoder）在生成模型上的变体。基于深度学习的聚类模型选用不同的神经网络提升聚类效果，AE、VAE、生成式对抗网络（GAN ，Generative Adversarial Networks）用于聚类的原理类似。

VAE要求AE的中间特征服从给定的高斯分布，通过变分推断法推断出样本概率的最大下界，最大化下界的过程会使样本的中间特征逼近给定的先验分布。

3 系统应用与分析

故障的发生具有突发性和隐蔽性，故障诊断和预测有较大难度。本文采用“PCA+Louvain+UMAP”的降维聚类算法，以高铁动车组客室空调的数据分析为例，说明高铁动车组智能运维数据分析系统的应用。高铁动车组客室空调故障是动车组夏季常见的故障之一，动车组在运行过程中车体呈全密闭式，当空调制冷系统发生故障时，车内室温不断升高，将影响车内乘客的乘车环境，甚至可能导致动车组无法继续运行，严重影响动车组运行秩序[3]。

3.1 数据处理

本文选取动车组客室空调相关部件传感器数据用于分析其健康状况的特征，数据来源为20列CRH380B型和20列CRH380BL型动车组在2020年6月～8月运行期间的客室空调相关WTDS数据，共4 725 120条记录，每条记录的10维特征选取如表1所示。

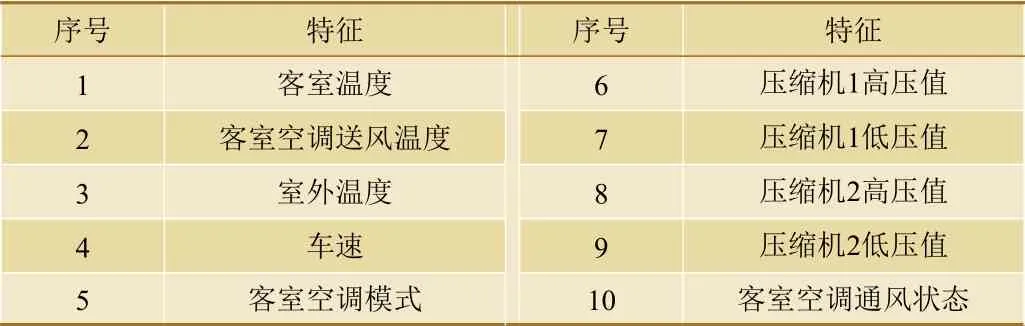
表1 客室空调特征列表

本文对选取的10维特征进行缺失值处理、去量纲等数据预处理，并结合业务知识和经验[12]对其进行特征扩展，新的特征与客室空调故障有更好的相关性，有助于进行数据分析。最终将特征从10维扩展至16维，扩展后的特征如表2所示。

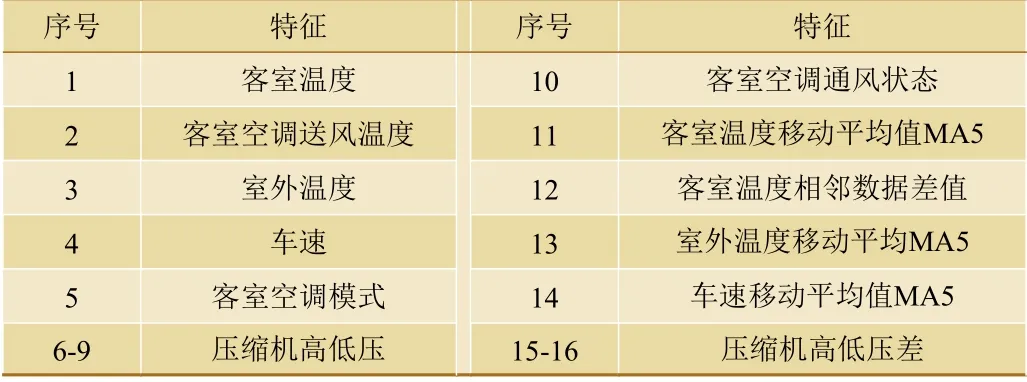
表2 扩展后的客室空调特征列表

3.2 降维聚类

（1）降维：对扩展后的16维特征数据，利用PCA方法进行线性降维，降维结果如图3所示，横坐标代表主成分的序号，纵坐标代表主成分对应的标准差。由图3可知，大部分信息在前9个主成分中捕获，因此，选择前9个主成分进行后续分析。

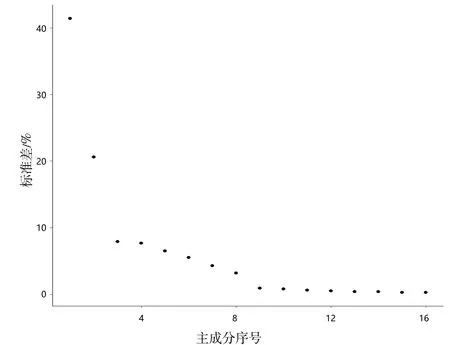
图3 PCA降维的成分分析

（2）聚类：选择降维后数据的前9个主成分作为输入，利用Louvain算法进行基于图的聚类，其中resolution参数为0.5。

（3）可视化：对于聚类后的数据进行UMAP降维，在2维空间上进行可视化展示，如图4所示，以供专业人员进行结果分析。

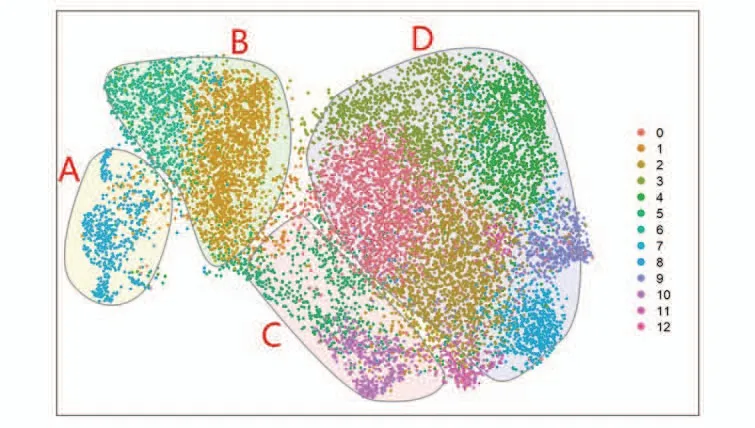
图4 动车组客室空调健康状况降维聚类结果

3.3 结果分析

对16维特征数据进行“PCA+Louvain+UMAP”降维聚类分析的结果如图4所示，数据被聚类为12个类别，不同的颜色代表不同的类别。专业人员通过对结果的分析发现，可将图中的12个类别划分为4类区域A、B、C和D，各类数据的主要特征如表3所示。

表3 各类数据对应的主导特征列表

A类数据为一级故障预警；B类数据为二级故障预警；C类数据为三级故障预警；D类数据为客室空调健康状态下的数据，可被分类为正常[12]。

3.4 数据标注

根据图4的聚类效果和结果分析，发现动车组客室空调健康状况是可划分的，并且划分后的4类区域可反映不同程度的客室空调健康状况，说明16维特征的选取是合理的，可作为特征工程环节的输出。在建模分析阶段可将这16维特征作为特征池，形成客室空调健康度判定算法。同时，可将A、B、C、D这4种分类的聚类结果转换为客室空调健康度的数据标签。标注后的数据作为模型分析系统的输入，利用监督学习的方法，形成客室空调故障诊断和预测方法。

4 结束语

本文概述了高铁动车组智能运维算法研究平台的总体架构，着重阐述了高铁动车组智能运维数据分析系统的构建，包括关键算法和数据处理流程。并以高铁动车组客室空调故障的数据分析为例进行了应用研究与分析，证明了该系统的可用性。

下一步应进行的工作包括：（1）利用“降维—聚类”的算法框架完成塞拉门、轴承类等部件的特征工程和数据标注；（2）利用特征工程和数据标注的结果，建立有监督的客室空调健康评估模型，实现客室空调故障诊断和预测。