基于遥感数据同化的土壤含盐量估算方法

2022-08-08张智韬黄小鱼陈钦达张珺锐

农业机械学报 2022年7期

张智韬黄小鱼陈钦达张珺锐台翔韩佳

(1.西北农林科技大学旱区农业水土工程教育部重点实验室，陕西杨凌 712100；2.西北农林科技大学水利与建筑工程学院，陕西杨凌 712100)

0 引言

土壤盐渍化是导致干旱半干旱地区土地退化的重要成因，土地退化会引起农作物减产，进而影响国家和社会的可持续性发展[1]。因此，准确连续地监测土壤含盐量对灌区的农业和经济发展有着十分重要的现实意义。

卫星遥感已经成为监测土壤含盐量的重要手段[2]，遥感反演具有快速、准确地大面积监测土壤含盐量的优点[3]，但是其在时间上不连续，只能反映卫星过境时刻的瞬时状态，并且无法揭示土壤盐分运移的内在机制以及其与气象、土壤、植被等因素的关系。盐分运移模型通过输入气象数据、土壤参数等，在时间序列上能连续模拟单点尺度的土壤含盐量[4]，但是其受模型输入数据的不确定性限制，导致模型误差在时间上不断累积，因而模拟精度不高。数据同化能够把遥感信息和盐分运移模型各自的优势相结合，能较为准确地连续监测区域土壤含盐量的时空变化情况，是精准农业的发展趋势。

数据同化就是通过引入时间序列的观测数据来校正模型模拟过程，从而提高模型模拟精度[5]。陈鹤等[6]构建集合卡尔曼滤波数据同化方案，将其输入到HELP模型中，有效地提高了土壤水分的模拟精度。王泽人等[7]以集合卡尔曼滤波为基础，构建太湖叶绿素a质量浓度同化试验系统，提高了太湖蓝藻水华的预测精度。上述研究是基于实测数据在单点尺度的数据同化，而未基于遥感数据开展区域尺度的数据同化研究，因此同化结果具有一定的局限性。文献[8-11]采用同化算法把遥感数据同化到模型中，开展区域尺度数据同化研究，多应用在产量估计、土壤水分等方面，关于区域尺度的土壤含盐量同化研究较少。

本文以高分一号卫星影像为数据源，结合研究区不同深度时间序列的实测土壤含盐量，以岭回归法遥感反演的土壤含盐量模型作为观测算子，采用集合卡尔曼滤波同化算法将遥感反演值引入到HYDRUS-1D模型中，对不同深度的土壤盐分运移过程进行同化模拟，通过对集合数进行敏感性分析，确定单点尺度数据同化方案的最佳集合数，从而得到最佳的单点尺度监测土壤含盐量数据同化方案，并由此扩展到区域尺度监测土壤含盐量的数据同化研究，采用同化遥感数据为连续准确地监测土壤含盐量时空变化提供了可行方案。

1 材料与方法

1.1 研究区概况

研究区位于内蒙古河套灌区沙壕渠灌域(40°52′～41°00′N，107°05′～107°10′E)，形状类似于狭长型的倒三角形，整体地势呈南高北低。沙壕渠灌域地处干旱半干旱地区，属于典型的温带大陆性气候，灌域内常见作物有小麦、葵花、玉米等，灌溉用水多数来自于过境的黄河水，年平均降水量约为140 mm，年平均蒸发量约为2 000 mm，降水少、蒸发大的特点以及长期的不合理灌溉方式，使得研究区的土壤盐渍化问题日趋严重。

1.2 田间实测数据

本研究在沙壕渠灌域内共设置120个采样点，研究区及采样点分布如图1所示。采用五点法对每个采样点深度0～20 cm、20～40 cm、40～60 cm进行分层采样，用手持GPS仪器记录该采样点的具体位置信息，将土样放置到已编号的铝盒中，并带回实验室。采用干燥法测定土壤含水率。把土样研磨配制成土水比为1∶5溶液，经过搅拌、静置、沉淀、过滤等操作后，并使用电导率仪(DDS-307A型，上海佑科仪器公司)测定土壤电导率，取每个采样点的5个电导率平均值作为该采样点的电导率，并通过经验公式[12]计算土壤含盐量(SSC，%)。采样时间分别为2019年4月15日、5月1日、5月15日、6月1日、6月15日、7月1日、7月15日、8月1日、8月15日、9月1日和9月15日，共11次。

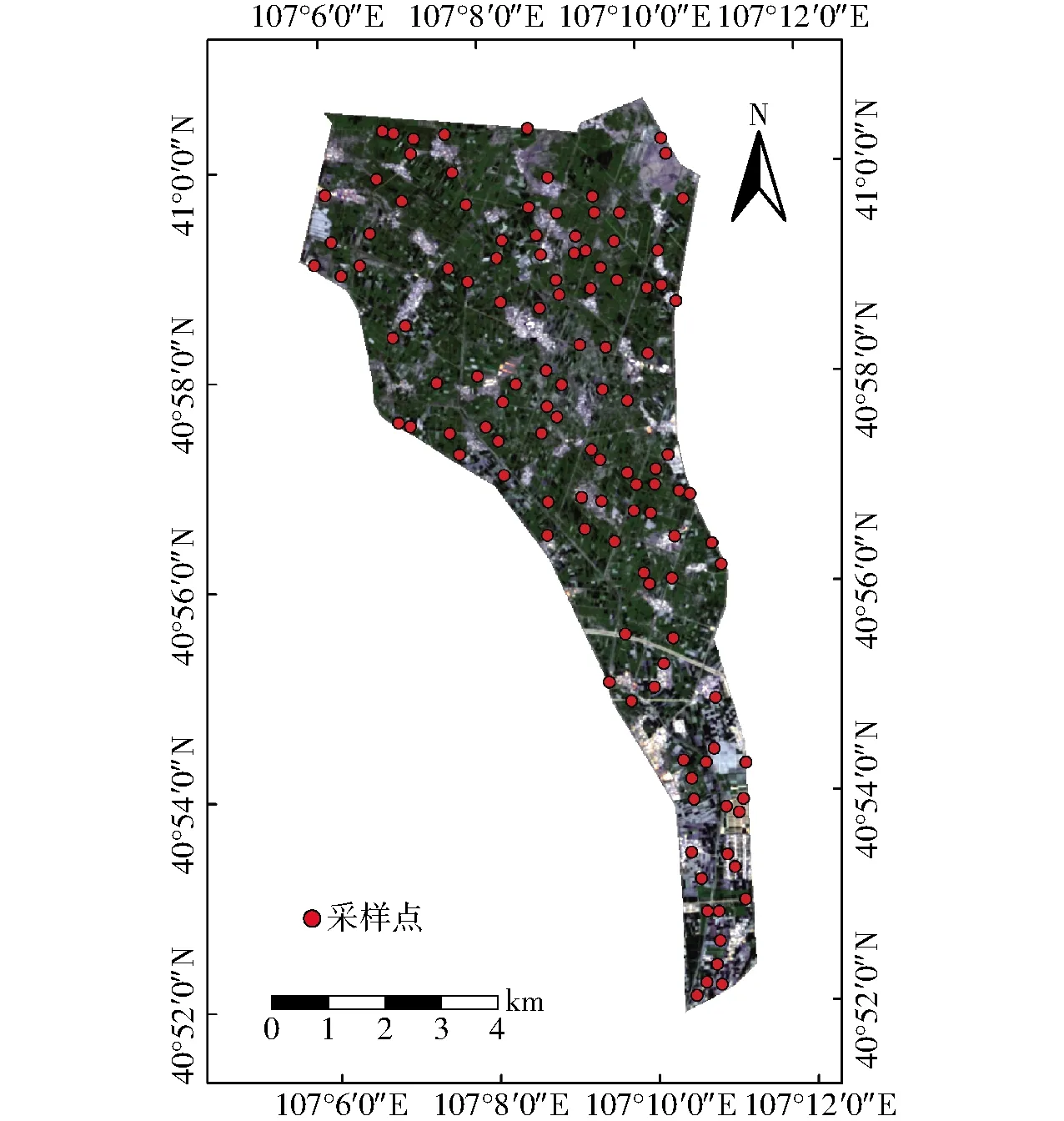
图1 研究区及采样点分布图Fig.1 Map of study area and distribution of sampling points

1.3 遥感反演土壤含盐量

遥感数据来自于中国卫星资源应用中心(http:∥www.cresda.com/CN/)的高分一号卫星。遥感数据预处理包括几何精校正、辐射校正、大气校正、裁剪等过程，并提取波段反射率，进而计算光谱指数。本研究采用4个波段反射率组合的光谱指数，共计24个，分别为SI-T、BI、SI、SI1、SI2、SI3[13]、S1、S2、S3、S5、S6、NDSI[14]等12个盐分指数和CRSI[15]、SR、NDVI、EVI、DVI、TVI、SRVI[16]、MSAVI[17]、ARVI[18]、NDWI[19]、NDGI[20]、GRVI[21]等12个植被指数。在模型构建过程中，盐分指数和植被指数分别经过灰度关联法筛选，选取排序前4的盐分指数和植被指数的光谱指数组合作为输入反演模型的自变量，以不同深度的实测土壤含盐量为因变量，把所有采样点的土壤含盐量按照从小到大排序，每隔2个样本选取出1个样本作为验证集，其余则为建模集，分别对建模集和验证集构建基于不同深度土壤含盐量的岭回归法反演模型，得到不同深度的土壤含盐量遥感反演值。卫星遥感影像获取的时间分别为2019年5月1日、5月13日、5月30日、6月28日、7月1日、7月30日、8月7日、8月15日、9月1日和9月18日。

1.4 HYDRUS-1D模型

HYDRUS-1D模型适用于模拟一维条件下饱和-非饱和多孔介质的水分、能量、溶质运移以及根系吸水等[22]。本研究主要使用HYDRUS-1D模型的水分运移模块和溶质运移模块，不考虑根系吸水模块。在开展土壤盐分运移模拟时，需要输入的数据包括气象数据、地下水位、初始条件及模型相关参数等。气象数据来自于中国气象数据网(http:∥data.cma.cn/)，包括降水量、蒸发量、气温、风速、日照时数等气象要素。选取河套灌区内的杭锦后旗、临河、五原、磴口、乌拉特前旗等5个气象站，对这些站点的逐日气象要素进行克里金插值。根据气象数据，使用Penman-Monteith公式计算潜在蒸散发量[23]。模型的土壤水力特征参数、溶质运移参数等的初始值基于已有的研究选定[24-25]，通过比较不同深度的实测土壤含盐量与模拟值的偏差，不断地对模型参数值进行调整，从而确定HYDRUS-1D模型主要参数的具体值。选取大气边界作为水分运移模块的上边界，变压力水头作为水分运移模块的下边界；溶质运移模块的上、下边界条件均为浓度边界。初始条件为初始时刻实测的土壤含水率和土壤电导率。

1.5 集合卡尔曼滤波数据同化方案

1.5.1集合卡尔曼滤波原理

集合卡尔曼滤波作为顺序数据同化算法之一，它以蒙特卡罗方法为基础，采用一组符合高斯分布的随机变量集合，通过模型向前积分，计算下一时刻状态量的统计特征[26]。它很好地解决了卡尔曼滤波在实际应用中误差协方差矩阵的估计，克服了卡尔曼滤波线性化的问题[27]。

(1)进行初始化。假设有N个集合数，在t时刻，添加高斯白噪声，从而对土壤含盐量进行初始扰动，得到符合高斯分布的状态变量集合Xi,0(i=0，1，…，N)。

(2)把t时刻的土壤含盐量集合输入到HYDRUS-1D模型中，得到t+1时刻的土壤含盐量预测值集合，计算式为

(1)

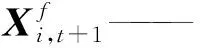
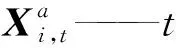
Mt,t+1——模型算子，本研究为HYDRUS-1D模型

ωi,t——模型误差，服从期望为0、方差为Qt的高斯分布

Qt——t时刻模型误差扰动所对应的误差协方差矩阵

(3)计算t+1时刻土壤含盐量预测值集合的均值和误差协方差矩阵，计算式为

(2)

(3)

(4)计算t+1时刻卡尔曼增益，计算式为

(4)

(5)

(6)

式中Kt+1——t+1时刻的卡尔曼增益

Ht+1——t+1时刻的观测算子

Rt+1——t+1时刻观测误差扰动所对应的误差协方差矩阵

(5)计算t+1时刻土壤含盐量分析值集合的均值和误差协方差矩阵，计算式为

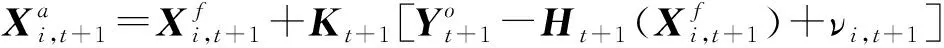
(7)

(8)

(9)

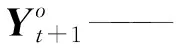
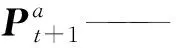
νi,t+1——观测误差，服从期望为0、方差为Rt+1的高斯分布

1.5.2不同深度土壤含盐量集合卡尔曼滤波数据同化方案

数据同化系统由观测算子、模型算子和同化算法3部分组成，在本研究中，观测算子为时间序列上基于不同深度土壤含盐量的岭回归法反演模型，模型算子为HYDRUS-1D模型，模拟时间序列上不同深度土壤盐分运移，同化算法则为耦合观测算子(遥感数据)和模型算子(模型模拟数据)的集合卡尔曼滤波，在考虑集合数、观测误差以及模型误差等同化条件的基础上，通过同化遥感数据到HYDRUS-1D模型中，开展单点尺度不同深度土壤含盐量数据同化方案，进而将单点同化方案扩展到不同深度的区域尺度土壤含盐量数据同化方案。其流程如图2所示。

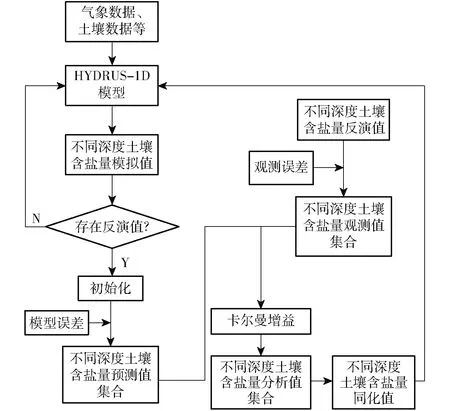
图2 数据同化流程图Fig.2 Flow diagram of data assimilation

(1)开始进行HYDRUS-1D模型模拟，得到t时刻不同深度土壤含盐量模拟值。

(2)t+1时刻分2种情况：①当t+1时刻不存在反演值时，t时刻的不同深度土壤含盐量模拟值继续输入HYDRUS-1D模型中，得到t+1时刻的不同深度土壤含盐量模拟值。②当t+1时刻存在反演值时，开始数据同化的计算流程。对t时刻不同深度土壤含盐量模拟值进行初始化，并输入到HYDRUS-1D模型中，再加上模型误差生成不同深度土壤含盐量预测值集合；利用t+1时刻不同深度土壤含盐量反演值加上观测误差生成不同深度土壤含盐量观测值集合；通过预测值集合和观测值集合计算卡尔曼增益，更新得到不同深度土壤含盐量分析值集合，并计算其均值，即为同化值。

进入下一时刻，重复步骤(2)的计算流程，直至整个同化研究结束。

本研究以不同深度土壤含盐量作为数据同化方案的状态变量，以多时相岭回归法反演模型为观测算子，通过集合卡尔曼滤波同化算法将其引入HYDRUS-1D模型中，HYDRUS-1D模型模拟时间为2019年4月15日至9月21日，共160 d，在2019年4月15日对HYDRUS-1D模型输入初始时刻不同深度土壤含盐量实测值，模拟时间序列上不同深度土壤盐分运移。模型运行到2019年5月1日，即第1次出现遥感反演值时，开始进行数据同化，同化时间取为2019年5月1日至9月21日，共144 d。

1.6 评价指标

本研究采用决定系数R2、相对误差(RE)对遥感反演结果进行评价；采用均方根误差(RMSE)、同化效率系数(EFF)[28]和归一化还原误差指数(NER)[29]对单点尺度同化结果进行评价；采用相关系数r和NER对区域尺度同化结果进行评价。其中，EFF和NER的计算公式分别为

(10)

(11)

式中EFF——同化效率系数

NER——归一化还原误差指数

Ot——t时刻的土壤含盐量实测值

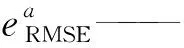
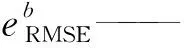
EFF的取值范围为-∞～1，当EFF大于0时，HYDRUS-1D模型模拟结果的精度提高，当EFF小于0时，HYDRUS-1D模型模拟结果精度降低。EFF越接近1，精度越高。

NER的取值范围为-∞～1，当NER大于0时，表明改善了HYDRUS-1D模型模拟结果；当NER小于0时，表明降低了HYDRUS-1D模型模拟结果。NER越接近1，精度越高。

2 结果与分析

2.1 基于光谱指数的土壤含盐量估算

以2019年6月28日的高分一号卫星遥感图像为例，使用灰色系统把120个采样点不同深度土壤含盐量实测值分别与12个盐分指数、12个植被指数进行灰度关联分析，它们的灰色关联度和排序如表1、2所示。本研究分别选取关联度排序前4的盐分指数和植被指数构成的光谱指数组合作为自变量，以不同深度的实测土壤含盐量作为因变量，构建基于岭回归法的不同深度土壤含盐量反演模型。模型的建模和验证结果如表3所示。

表1 不同深度盐分指数与土壤含盐量的灰色关联度Tab.1 Gray correlation degree between salinity index and soil salinity at different depths

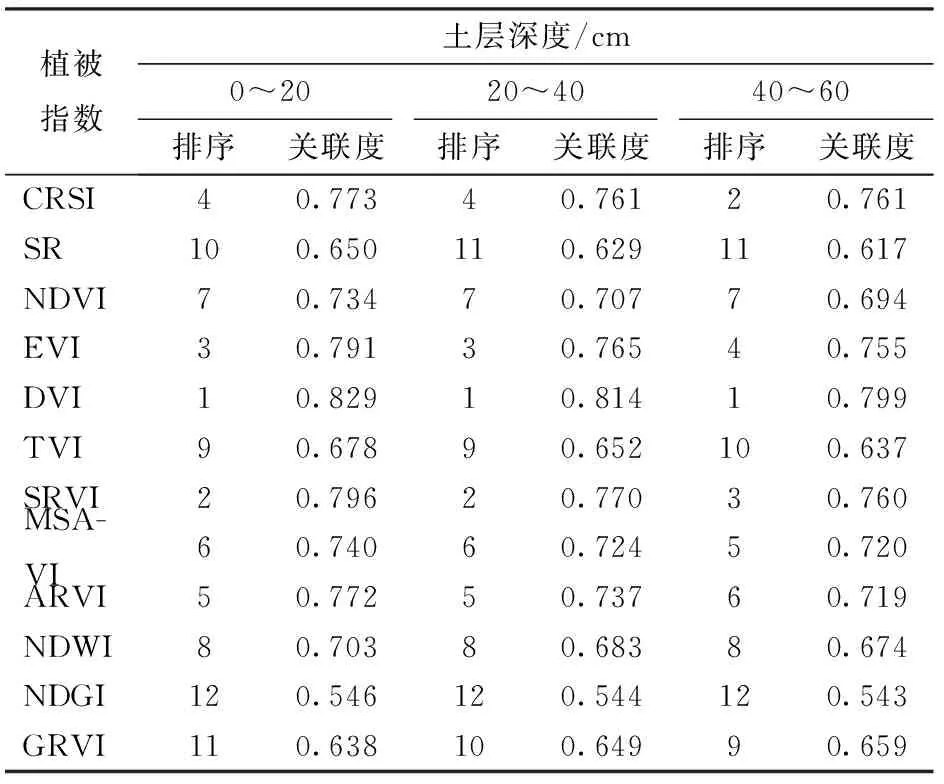
表2 不同深度植被指数与土壤含盐量的灰色关联度Tab.2 Gray correlation degree between vegetation index and soil salinity at different depths

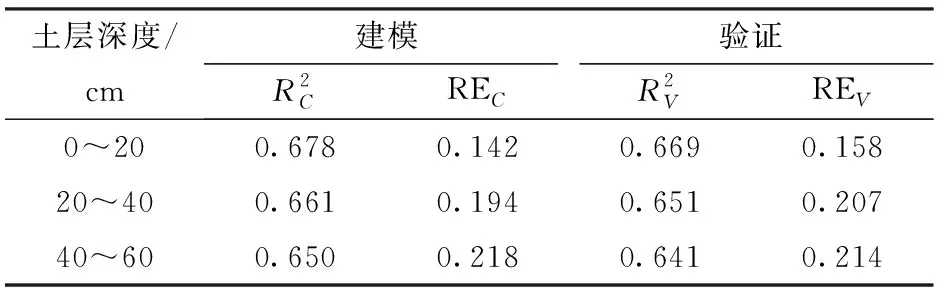
表3 基于不同深度土壤含盐量的岭回归法模型Tab.3 Ridge regression models based on soil salinity at different depths

由表3可知，同一深度上，岭回归法模型的建模集和验证集的决定系数R2和相对误差RE相差不大，并且随着深度的增加，模型精度随之降低。0～20 cm模型反演精度最高，其次是20～40 cm，模型反演精度最差的是40～60 cm。在3个深度上，岭回归法模型的建模集和验证集的R2均达到0.64以上，拟合精度较高，建模集和验证集的RE介于0.14～0.22之间，表明使用岭回归法模型得到的遥感反演值与实测值的误差相对较小，模型反演精度较高。

使用岭回归法模型得到其余时刻的不同深度土壤含盐量遥感反演值，并把时间序列上的不同深度土壤含盐量遥感反演模型作为数据同化方案的观测算子，开展不同深度的土壤含盐量数据同化研究。

2.2 单点数据同化方案

2.2.1集合数的敏感性分析

基于不同深度土壤含盐量的集合卡尔曼滤波数据同化方案，集合数是影响数据同化模拟精度的重要因素。本研究设置的集合数分别为10、25、50、75、100，对不同深度的土壤盐分运移进行同化模拟，分析集合数对同化结果的影响，如图3所示。

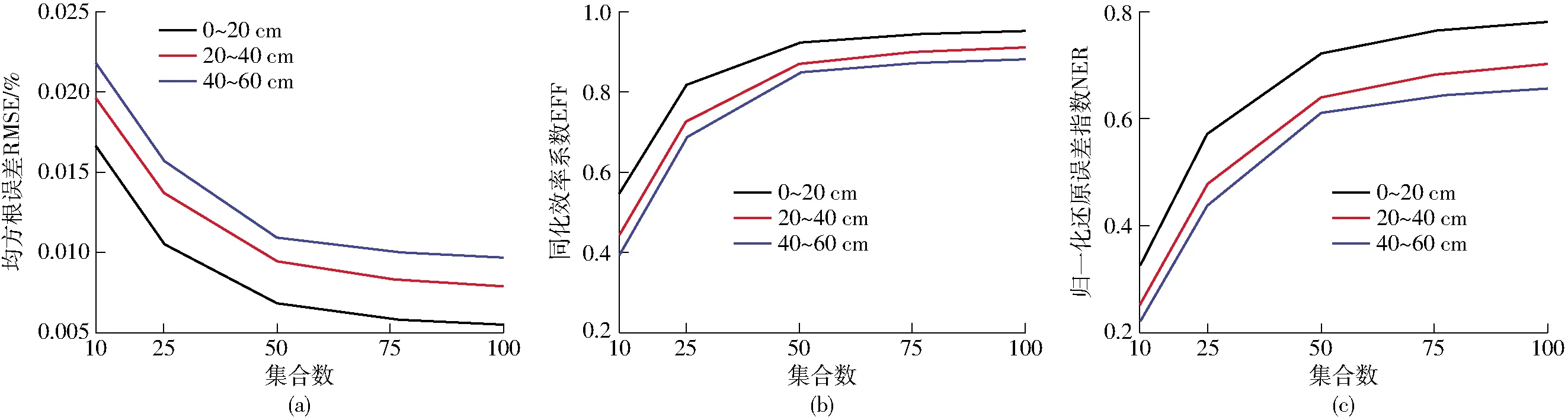
图3 不同集合数对同化结果的影响Fig.3 Effects of different ensemble numbers on assimilation results

由图3a可知，随着集合数的增大，每个深度土壤含盐量同化值的均方根误差RMSE都随之减小。当集合数小于等于50时，RMSE降低速度较大；当集合数大于50时，RMSE降低速度相对较小。当集合数为10和25时，RMSE均高于0.01%；当集合数为50时，RMSE介于0.006%～0.011%之间；当集合数为50、75和100时，其RMSE相差不大。由图3b可知，每个深度土壤含盐量同化值的同化效率系数EFF都大于0，说明在不同的集合数条件下，均具有同化效果。各深度的EFF都随着集合数增加而增加，增加的速度在减小，当集合数为10时，同化效果最差，各深度的EFF都小于0.55；当集合数为25时，同化效果相对较差；当集合数为50时，各深度的EFF均达到0.8以上，表明经过数据同化后，提高了HYDRUS-1D模型模拟精度，同化效果较好；当集合数为75和100时，各深度的EFF与集合数为50时的EFF相差不大。由图3c可知，每个深度土壤含盐量同化值的归一化还原误差指数NER均大于0，说明在不同的集合数条件下，土壤含盐量模拟精度均得以提高。各深度的NER变化趋势表现为随着集合数的增加而增加，增加的趋势在减缓，当集合数为10和25时，各深度的NER均低于0.6，表明同化方案对改善模型模拟精度的能力较差；随着集合数的增加，当集合数为50时，NER介于0.61～0.73之间；当集合数为75和100时，与集合数为50时的NER相差不大。综上所述，为了提高同化运算效率和满足同化精度的要求，本研究的最佳集合数为50。

由图3可知，当集合数相同时，各深度同化值的RMSE均表现为随着深度的增加而增大，而各深度同化值的EFF和NER都表现为随着深度的增加而减小。在3个深度上，0～20 cm同化值的RMSE最小，EFF最大，NER最大，0～20 cm同化效果最好；20～40 cm次之；40～60 cm最差，其RMSE最大，EFF最小，NER最小。故同化精度是随着深度的增加而降低。

2.2.2单点同化结果分析

根据上述研究，集合数取为50，观测误差和模型误差分别设置为0.01、0.01，对单点尺度不同深度土壤含盐量开展集合卡尔曼滤波同化研究。基于不同深度的土壤含盐量实测数据(简称实测值)，采用HYDRUS-1D模型模拟得到土壤含盐量模拟值(简称模拟值)、采用岭回归法模型反演得到土壤含盐量遥感反演值(简称反演值)、采用集合卡尔曼滤波同化算法得到土壤含盐量同化值(简称同化值)，比较不同深度土壤含盐量的模拟值、反演值、同化值和实测值，如图4所示，并进行误差分析，如表4所示。

图4 不同深度土壤含盐量的模拟值、反演值、同化值与实测值的比较Fig.4 Comparisons of simulated values, inversion values, assimilation values and measured values of soil salinity at different depths

由图4可知，在同一深度上，模拟值与实测值的误差最大，其次是反演值，同化值最接近实测值；在不同深度上，模拟值、反演值和同化值与实测值的误差都随着深度的增加而增加。由表4可知：①从同化误差的角度分析，在同一深度上，与模拟值、反演值相比，同化值与实测值的误差最小，其在3个深度的RMSE均低于0.011%，反演值次之，反演值的RMSE与同化值的RMSE相差不大，模拟值与实测值的误差最大，其在3个深度的RMSE为0.024%～0.028%；在3个深度上，同化值、反演值和模拟值的误差随着深度的增加而增加，表明无论是模型模拟、遥感反演还是同化模拟对土壤含盐量的作用都是表层优于深层。②就同化效率系数而言，在同一深度上，同化值和反演值的EFF大于0.65，并且同化值的EFF更接近于1，表明引入反演值到HYDRUS-1D模型中进行同化模拟，能较好地改善模型模拟精度，使同化值更接近实测值；在3个深度上，同化值和反演值的EFF都为正值，同化值的EFF大于反演值的EFF，它们的EFF随着深度的增加而降低，表明引入遥感数据对0～20 cm土壤含盐量的同化作用优于20～40 cm、40～60 cm。③从提高模型精度程度来看，在同一深度上，同化值和反演值的NER均大于0.4，并且同化值大于反演值，表明同化遥感数据，使得模型的模拟轨迹更加接近实测值，减小了模拟值与实测值的误差，提高了HYDRUS-1D模型的模拟精度；在3个深度上，同化值和反演值的NER都为正值，随着深度的增加，同化值和反演值的NER逐渐减少，表明同化遥感数据对每个深度土壤含盐量的模拟精度均能提高，并且对于每个深度的土壤含盐量，同化作用随着深度的增加而减小。

表4 不同深度土壤含盐量的模拟值、反演值、同化值与实测值的误差分析Tab.4 Error analysis of simulated values, inversion values, assimilation values and measured values of soil salinity at different depths

综上所述，在同一深度上，同化值与实测值最为接近，反演值次之，模拟值和实测值相差最大。在3个深度上，同化值、反演值和模拟值的精度都是随着深度的增加而降低。在单点尺度上，开展不同深度的集合卡尔曼滤波数据同化方案，结合了遥感反演和模型模拟各自的优势，通过集合卡尔曼滤波同化算法把时间序列上的不同深度土壤含盐量反演值应用到HYDRUS-1D模型，提高了土壤剖面模拟精度，得到了较为准确的同化值。并且引入遥感数据对各深度土壤含盐量的同化作用随着深度的增加而减小，0～20 cm土壤含盐量的同化模拟优于20～40 cm，40～60 cm最差。

2.3 区域数据同化方案

本研究开展区域尺度的不同深度土壤含盐量集合卡尔曼滤波数据同化模拟，在不同采样时间，基于区域尺度的实测值、反演值、模拟值以及同化值，通过r和NER计算它们与实测值之间的误差，以2019年6月15日为例，由表5可知，在3个深度上，模拟值的精度随着深度的增加而减小，表明HYDRUS-1D模型对于0～20 cm的土壤含盐量模拟精度较高，而20～40 cm、40～60 cm的土壤含盐量模拟精度相对较差。在3个深度上，反演值的精度随着深度的增加而减少，表明岭回归法模型对0～20 cm的土壤含盐量反演精度最高，20～40 cm反演精度次之，40～60 cm深度最差，但是20～40 cm、40～60 cm反演值的r和NER均较大，它们的模型反演精度较高。在3个深度上，同化值的同化精度随着深度的增加而降低，表明区域尺度的集合卡尔曼滤波数据同化方案对于0～20 cm土壤含盐量的同化效果最好，高于0～20 cm的反演值和模拟值。与0～20 cm相比，20～40 cm和40～60 cm同化值的r和NER相对较差，但仍优于同一深度的反演值和模拟值。它们的r和NER都是随着深度的增加而减小，表明0～20 cm同化值、反演值、模拟值的精度均为最高，它们在20～40 cm精度相对较差，在40～60 cm精度最差。在同一深度上，同化值与实测值的误差最小，其r为0.94～0.97，NER为0.61～0.69，反演值的精度次之，其与同化值的r相差较小，其NER为0.31～0.35，模拟值与实测值的误差最大，其r为0.65～0.72。在3个深度上，反演值和同化值的NER均大于0，并且同化值远高于反演值，表明区域尺度的集合卡尔曼滤波数据同化方案把遥感数据引入HYDRUS-1D模型中，能较好地监测区域尺度每个深度的土壤含盐量。

表5 区域尺度不同深度土壤含盐量模拟值、反演值、同化值与实测值的误差分析Tab.5 Error analysis of simulated values, inversion values, assimilation values and measured values of soil salinity at different depths in regional scale

故基于集合卡尔曼滤波同化算法开展区域尺度的数据同化研究，使得在区域尺度上，同化值优于反演值和模拟值，能更好地模拟区域尺度时间序列上不同深度土壤含盐量时空变化，从而更加接近实际情况。

以2019年6月15日为例，不同深度土壤含盐量同化图如图5所示。

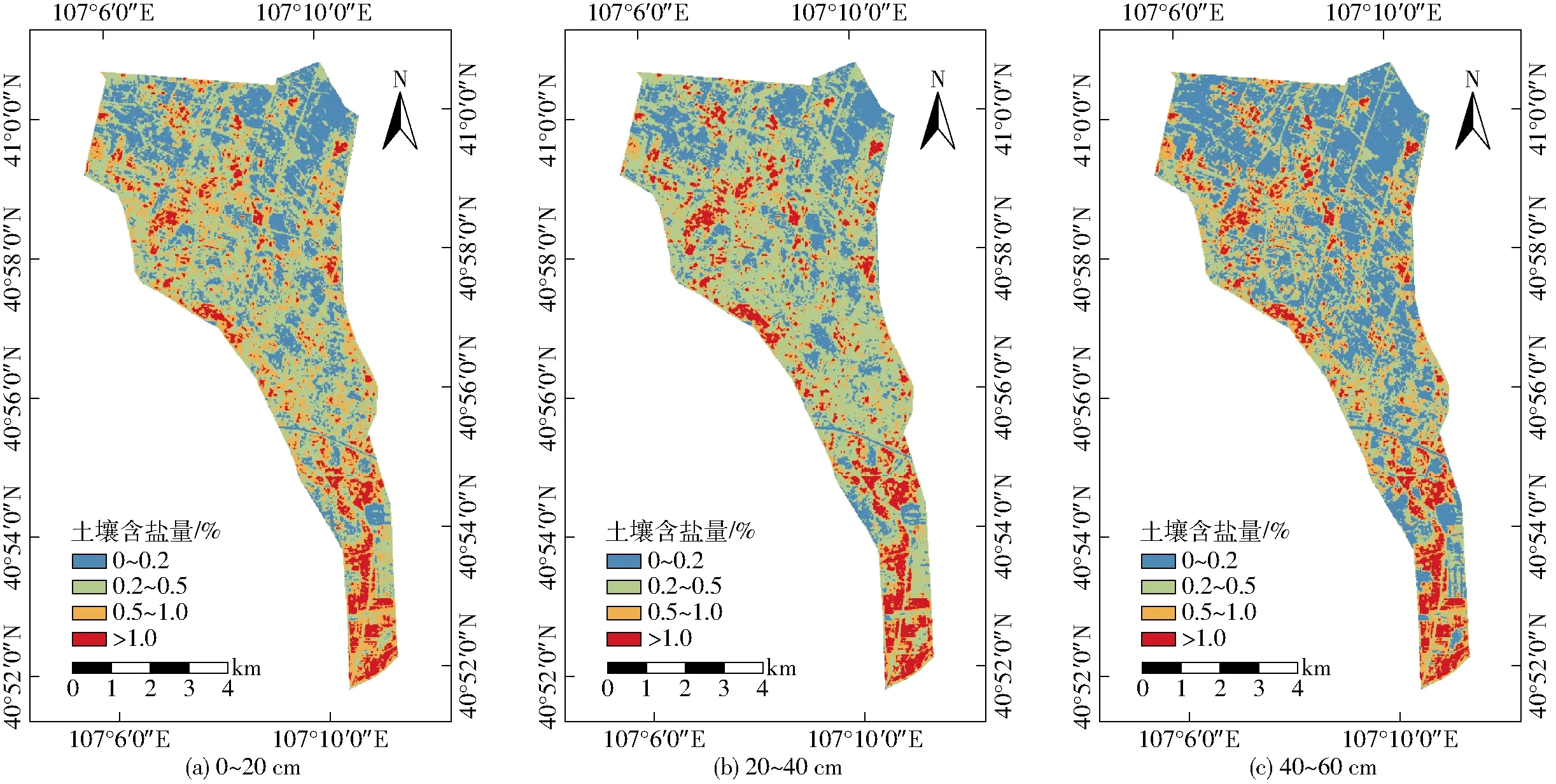
图5 不同深度土壤含盐量同化图Fig.5 Assimilation maps of soil salinity at different depths

3 讨论

在单点尺度上，与不同深度的模拟值和反演值相比，同化值与实测值更为接近，这是因为基于集合卡尔曼滤波同化算法把遥感数据同化到HYDRUS-1D模型中，提高了土壤剖面模型模拟精度，得到了更为准确的同化值，使得同化值与实测值的误差最小。同化精度随着深度的增加而减小，0～20 cm同化效果最好，20～40 cm次之，40～60 cm最差。本研究探究了集合数对单点尺度集合卡尔曼滤波数据同化方案的敏感性，结果表明集合数对同化模拟过程较为敏感，在各深度上均表现为随着集合数的增加，RMSE先大幅度降低，而EFF和NER则是先大幅度增加，然后达到相对稳定，故最佳的集合数为50，既能保证同化精度，又能提高同化运算效率。此外，还可以从同化频率[30]、观测误差[31]和引入不同深度的实测数据[32]等方面对数据同化方案进行敏感性分析，找到对数据同化方案的较为敏感性因素。

在区域尺度上，各深度的同化值与实测值的r均达到0.94以上，高于反演值和模拟值，并且各深度同化值的NER均在0.61以上，皆为正值，表明本研究能较好地应用于区域尺度的同化模拟，得到较为准确的时间序列区域尺度土壤含盐量时空变化信息。在区域尺度的集合卡尔曼滤波数据同化方案中，同化精度最好的深度为0～20 cm，其次是20～40 cm，40～60 cm最差，与单点尺度数据同化方案的结论一致。这是因为随着深度的增加，HYDRUS-1D模型的输入数据等对20～40 cm、40～60 cm土壤含盐量模拟的作用较小，导致它们与实测值的误差随着深度的增加而增加，并且岭回归法模型的反演精度随着深度的增加，也随之降低，在二者作用下，同化精度表现为随着深度的增加而降低。

本研究通过集合卡尔曼滤波同化遥感反演和模型模拟的土壤含盐量，开展区域尺度的不同深度土壤含盐量数据同化研究，有效地提高了时间序列的区域尺度土壤剖面含盐量模拟精度。一方面模型模拟弥补了遥感数据的不连续性问题，另一方面同化遥感数据可以提高模型模拟精度，但是同化结果仍存在误差，主要来源于遥感反演模型、HYDRUS-1D模型数据的不确定性和同化算法带来的误差。本研究使用的遥感反演模型为统计回归模型，未来研究可以采用机器学习模型提高遥感监测的精度[33]，把遥感数据引入到HYDRUS-1D模型中，对区域尺度的各深度土壤含盐量进行同化模拟，从而提高同化精度。在HYDRUS-1D模型中，土壤水力特征参数、溶质运移参数等都会对同化结果产生较大的影响。因此，为提高同化精度，不仅需提高反演模型精度，也需提高模型参数的精度，从而更为准确地监测区域尺度各深度土壤含盐量的时空变化，使同化结果更具有可靠性。

本研究只考虑了土壤含盐量作为状态变量，在开展区域尺度的同化模拟时，尚未考虑其他状态变量随时间变化的特性是否会对同化结果造成一定影响。因此，今后研究可以探讨多状态变量的数据同化方案，如同时同化状态变量和模型参数[34-35]，进一步准确地提高区域尺度土壤含盐量的同化精度，或是将来基于遥感数据与盐分运移模型的数据同化研究重点。此外，单一的同化算法仍存在一定的局限性，结合多种不同类型的同化算法，如集合-变分数据同化算法[36-37]，发展基于遥感数据的耦合多种同化算法的数据同化方案，或是未来利用数据同化方法获取大面积土壤含盐量时空信息的一个重要研究方向。并且，植被覆盖和人工作业等影响含盐量因素也是本研究考虑不足的地方。在植被覆盖阶段，遥感反演受植被覆盖度、土壤质地、作物种类等多种因素的影响，从而导致同化精度的降低。对于人工作业，如灌溉等，对土壤含盐量造成淋洗，同时它具有局部、粗化效应，从而对同化结果造成一定的影响。上述不足有待进一步深入研究。