三臂回转式水稻钵苗移栽机构反求设计与试验
2022-08-08吴国环俞高红周海丽葛彦杰叶阿康
吴国环 俞高红 周海丽 葛彦杰 叶阿康 王 磊
(1.浙江理工大学机械与自动控制学院, 杭州 310018; 2.温州职业技术学院智能制造学院, 温州 325000;3.浙江省种植装备技术重点实验室, 杭州 310018)
0 引言
行星轮系水稻钵苗移栽机构可由一套机构完成取苗、持苗和推苗等动作,其结构紧凑、工作连续平稳,能够克服连杆机构存在的问题,已经成为水稻钵苗移栽机构研究的一个重要方向[1-12]。浙江理工大学农业机械研究所提出了多种两臂非圆齿轮行星轮系水稻钵苗移栽机构[8-11],但当两臂水稻钵苗移栽机构移栽效率达到200株/(min·行)时移栽取苗成功率受到比较大的影响。文献[12]提出的三臂水稻钵苗移栽机构相对于两臂移栽机构,在同等移栽效率下,可允许行星架转速是传统两臂移栽机构的2/3,有利于提高移栽机构的取苗成功率。因此,三臂行星轮系水稻钵苗移栽机构的研制对提高水稻移栽机械化水平具有实际价值。但现有三臂移栽机构采用正向设计方法进行设计,即给定非圆齿轮机构参数,以输出的工作轨迹和姿态为目标,人机交互的方式确定各机构参数,无法同时满足良好的轨迹和姿态要求,在实际应用中仍存在移栽绝对运动轨迹前倾造成秧苗推倒、回带,以及植苗时的推苗角偏小造成推苗直立性欠佳的问题。而基于轨迹或位姿的反求设计能够实现机构参数与传动比、轨迹之间的关联设计[13-18]。俞高红团队[19]提出的正反求设计方法,在正向设计的基础上,局部调整其工作轨迹,基于调整后的工作轨迹反向求解总传动比,再采用一定的方法分配总传动比到两级非圆齿轮副,最后求解出非圆齿轮节曲线,该方法对解决原三臂水稻钵苗移栽机构存在的问题具有实际意义。
本文拟在文献[12]原机构的基础上,以解决目前移栽绝对运动轨迹前倾和推苗角偏小的问题为目标,预设较理想局部绝对运动轨迹,优化确定相对运动轨迹,开展移栽机构反求设计模型建立、优化设计软件开发及非圆齿轮设计等研究,通过理论分析、虚拟仿真及样机试验来验证所设计机构解决绝对运动轨迹前倾和推秧角偏小问题的效果。
1 移栽机构设计目标与工作原理
1.1 移栽机构设计目标
由文献[12]可知原三臂移栽机构的推苗角为55.32°,相对运动轨迹如图1a中曲线2所示,绝对运动轨迹如图1c所示,其绝对运动轨迹回程段在竖直秧苗线右侧(视为轨迹前倾),点D′、E′之间轨迹段尽量左凸,保证移栽臂推完苗后回程阶段向左上方运动,越过秧苗,避免出现移栽臂向前带苗的现象。通过分析可知,相对运动轨迹回程段越往左,则绝对运动轨迹回程段前倾程度越低,因此,本文在优化机构运动轨迹时,相对运动轨迹回程段应尽量左凸。
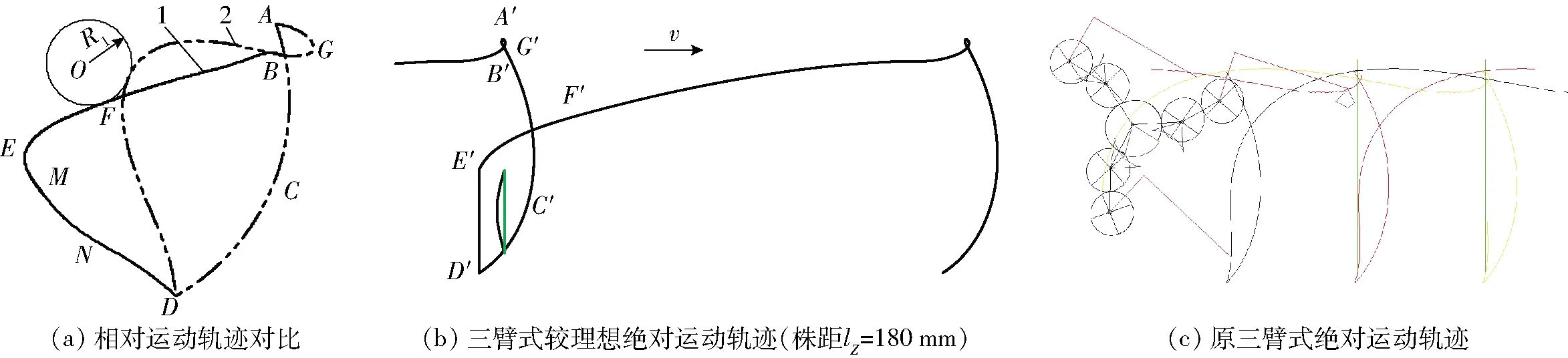
图1 水稻钵苗移栽轨迹Fig.1 Transplanting trajectory of rice seedling1.三臂式较理想相对运动轨迹 2.原三臂式相对运动轨迹
设计目标如下:①取苗角取值范围为10°~16°。②推苗角取值范围为60°~65°。③取苗角和推苗角的角度差范围为45°~55°。④移栽臂在地面以上推苗,当株距为180 mm时,移栽机构应近似实现如图1b所示的绝对运动轨迹(其对应的相对运动轨迹为图1a中的曲线1),D′E′回程段高度LD′E′≥120 mm(参考秧苗高度)。
1.2 机构工作原理
图2为三臂回转式水稻钵苗移栽机构示意图,机构中3个移栽臂对称布置,行星架转动一周,可以完成3次移栽作业。本文以右下侧为例,说明移栽机构工作原理。太阳轮与机架固定,动力输入轴带动行星架顺时针转动,此时凹锁止弧16和凸锁止弧进入啮合状态,一级中间轮17、二级中间轮15以及行星轮18相对于行星架静止,移栽臂19形成ABCD段夹持钵苗轨迹段;当凹凸锁止弧分离时,一级中间轮17与太阳轮开始啮合,二级中间轮15与一级中间轮17同轴转动,从而带动与二级中间轮15啮合的行星轮18,此时与行星轮18固连的移栽臂19开始转动并在轨迹最下端点D处推苗(地面以上),推苗完成后,行星架继续转动,移栽臂19的尖点形成DEFB段回程轨迹和BGA段取苗轨迹,其中环扣最远点G为取苗位置。
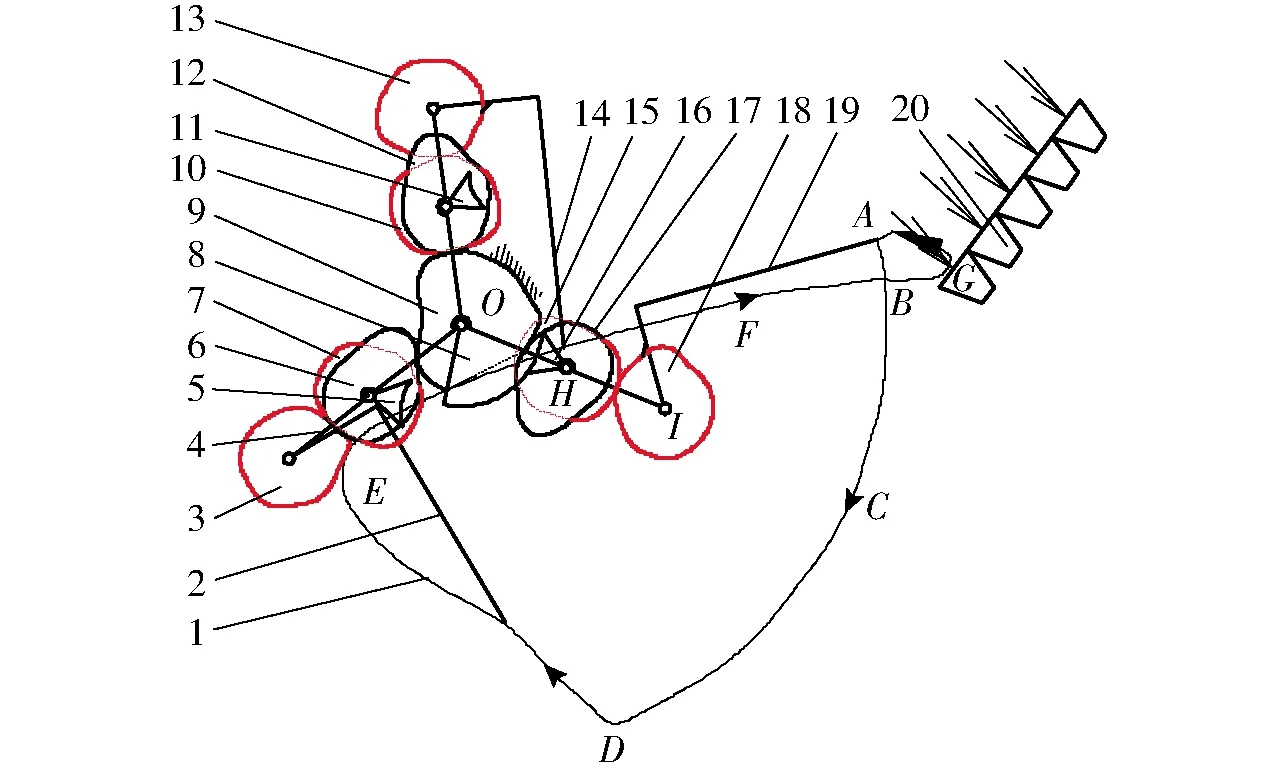
图2 三臂回转式水稻钵苗移栽机构示意图Fig.2 Schematic of transplanting mechanism of three-arm rotary rice seedling1.移栽轨迹 2、14、19.移栽臂 3、13、18.行星轮 4.行星架 5、11、16.凹锁止弧 6、12、17.一级中间轮 7、10、15.二级中间轮 8.凸锁止弧 9.太阳轮 20.钵苗盘
2 移栽机构反求设计
2.1 相对运动轨迹关键点分析
将移栽机构模型转化为平面2R杆开链机构模型,移栽机构关键位置及移栽机构夹苗片尖点的相对运动轨迹如图3所示。以点O为原点、水平方向为x轴,垂直方向为y轴建立坐标系,其中点G为相对运动轨迹上距离行星架回转中心(原点O)最远的点,如图3b所示,当移栽机构运行到该点时,杆a和杆b共线,取苗点G坐标为
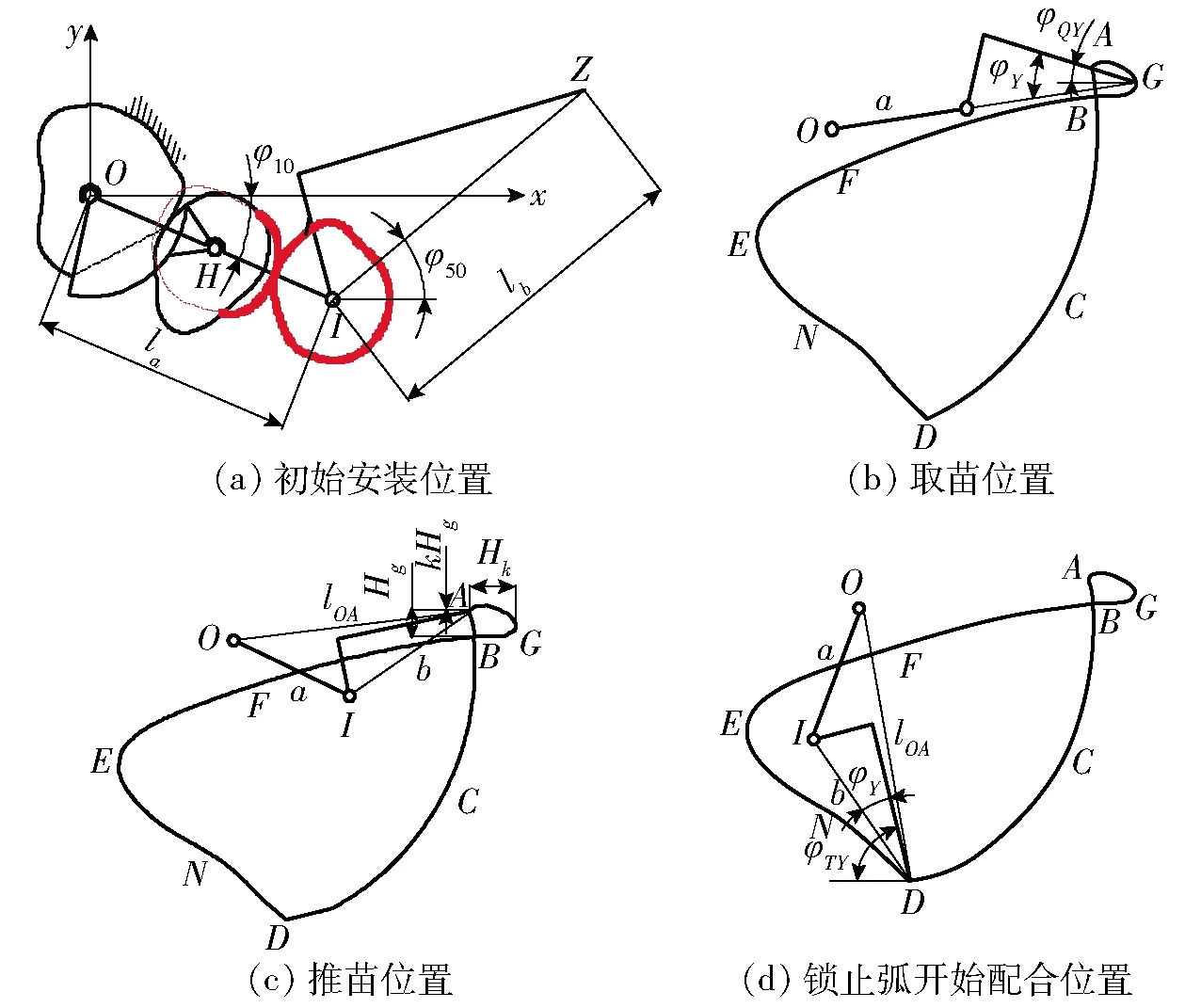
图3 移栽机构关键位置Fig.3 Key positions of transplanting mechanism
(1)
式中la——行星轮与太阳轮中心距,mm
lb——夹苗片尖点到行星轮回转中心I的距离,mm
φQY——取苗角,rad
φY——夹苗片所在直线和夹苗片尖点与行星轮回转中心I连线的夹角,rad
如图3c所示,根据几何关系求出锁止弧开始配合时点A的坐标为
(2)
式中k——小于1的系数,取0.6
Hk——相对运动轨迹环扣宽度,mm
Hg——相对运动轨迹环扣高度,mm
点A到原点O的距离为
(3)
当移栽臂夹苗片尖点运动到相对运动轨迹点A时,太阳轮和一级中间轮脱离啮合,锁止弧开始配合,杆a和杆b之间没有相对转动(图3d)。因此,AD段相对运动轨迹为圆弧,则推苗点D的坐标为
(4)
式中φTY——推苗角,rad
2.2 局部相对运动轨迹与绝对运动轨迹关系
夹苗片尖点的相对位移方程为
(5)
式中φ10——初始时行星架角位移,rad
φ30——初始时移栽臂角位移,rad
φ1——某一时刻行星架角位移,rad
φ3——某一时刻移栽臂角位移,rad
夹苗片尖点的绝对位移方程为
(6)
为便于计算,假设移栽机构绝对运动轨迹的回程轨迹为直线形,如图1b中D′E′竖直线段所示,则直线段夹苗片尖点Z的绝对位移方程为
(7)
结合式(5)~(7),基于D′E′竖直线段绝对运动轨迹可反求得到对应的局部相对运动轨迹,如图4中线段DM所示。为保证移栽机构近似实现图1b较理想绝对运动轨迹,在选取相对运动轨迹型值点时,令相对运动轨迹的线段DE向线段DM左侧(DNE1)调整。其中,点M为局部相对运动轨迹的最高点,点M和点D的垂直距离为120 mm。
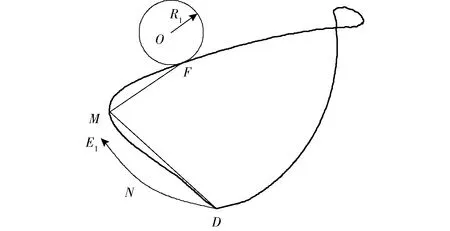
图4 反求出的局部相对运动轨迹Fig.4 Local relative motion trajectory obtained by inverse calculation
2.3 相对运动轨迹拟合
当机构关键参数与原机构取值相同时,通过局部较理想绝对运动轨迹反求得到局部相对运动轨迹,将其代替原移栽轨迹相应的局部轨迹,求得总传动比如图5所示,总传动比曲线峰值过大,不利于非圆齿轮齿廓生成,因此,需要对机构参数进行重新求解。由于图4相对运动轨迹的DMF段的形状决定了总传动比峰值,即∠DMF间接影响了总传动比峰值,同时约束了la、lb取值范围,所以利用∠DMF辅助确定相对运动轨迹。参考原机构参数及设计目标,初定∠DMF=78°,取苗角φQY=13°,推苗角φTY=65°,环扣宽度Hk=45 mm,环扣高度Hg=26 mm,la=120 mm,lb=150 mm,R1=lb-la,R2=lb+la。以R1、R2为半径的圆弧应与拟合好的轨迹分别外切和内切,点F和点G为切点。参考图4中DNE1路径选择6个坐标点作为拟合局部相对运动轨迹的型值点,在EG轨迹段选择12个型值点,在取苗段GA段选择7个型值点,其中点G为取苗点、点A为锁止弧开始配合点和点D为推苗点。用三次B样条曲线拟合相对运动轨迹,如图6所示。由于持苗阶段AD段轨迹为圆弧,不需要拟合该段轨迹。
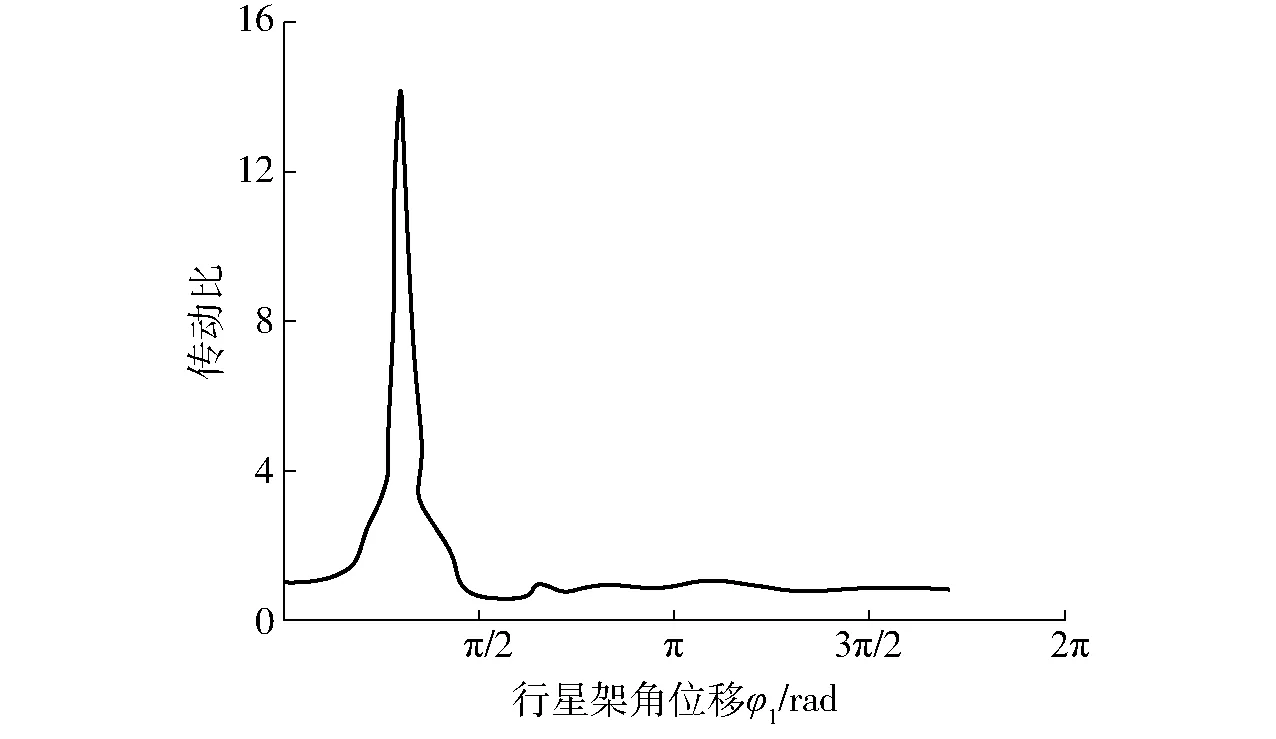
图5 原机构参数下总传动比Fig.5 Total ratio under original mechanism parameters
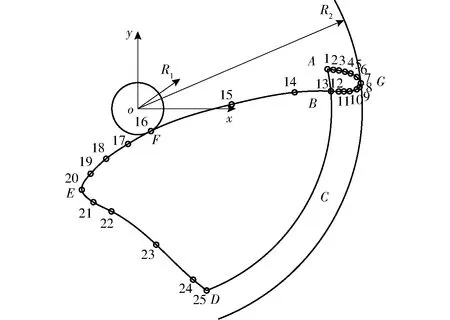
图6 相对运动轨迹曲线Fig.6 Fitting relative motion trajectory
2.4 传动比计算
用三次B样条曲线拟合出移栽机构夹苗片尖点的相对运动轨迹,根据拟合好的相对运动轨迹,反求出移栽机构行星轮旋转中心的位置,进而求出行星架和移栽臂的角位移,行星架角位移变化量和移栽臂角位移变化量比值即为该机构的总传动比。
行星轮旋转中心I的坐标为
(8)
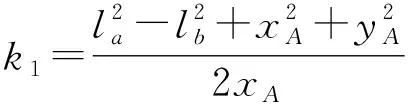
传动比为
(9)
其中
根据图6中相对运动轨迹反求移栽机构总传动比,如图7中曲线a所示,在总传动比曲线上选取25个能表现传动比曲线变化规律的型值点,调整传动比变化过大位置的型值点数值(传动比变化过大,则非圆齿轮曲率半径变化过大,无法获得齿廓[20]),最后用三次B样条曲线拟合这25个型值点,如图7中曲线b所示。
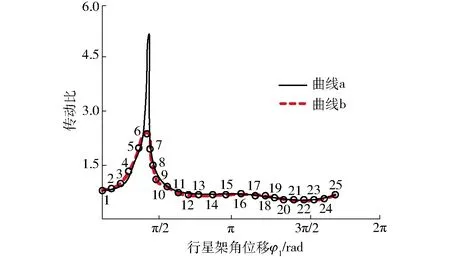
图7 传动比调整前后曲线对比Fig.7 Comparison of transmission ratio before and after adjustment
将总传动比分配到两级非圆齿轮传动中,初定第2级传动比i20为
(10)
在非圆齿轮的啮合传动过程中,单级非圆齿轮的主、从动轮节曲线作纯滚动,则只要保证主从动轮的节曲线周长相等,即可保证主从动轮同时旋转一周。为了实现这一目的,引入调整系数
(11)
式中φ2——中间齿轮角位移
第2级传动比i2为
i2=k2i20
(12)
第1级传动比i1为
(13)
节曲线方程的计算参考文献[19],本文不再赘述。
2.5 相对运动轨迹优化
基于Matlab编程软件,开发了水稻钵苗移栽机构的辅助分析与优化软件(图8),主要包括打开、反求局部相对运动轨迹、拟合相对运动轨迹、拟合传动比、获取轨迹点及获取传动比点等命令按钮,数据点区用于输入相对运动轨迹型值点和总传动比型值点数据。输入初定机构参数和局部绝对运动轨迹数据,反求得到局部相对运动轨迹关键型值点;结合局部相对运动轨迹输入完整相对运动轨迹的25个型值点,拟合相对运动轨迹并生成总传动比数据,点击选取25个总传动比型值点并输入软件、拟合总传动比,通过人机交互的方式获得一组满足设计目标的运动轨迹及机构参数,进而完成机构结构设计。总传动比曲线的峰值、谷值以及波动程度变化对移栽相对运动轨迹的影响显著,因此,主要研究总传动比关键型值点变化对相对运动轨迹的影响,如图9所示。
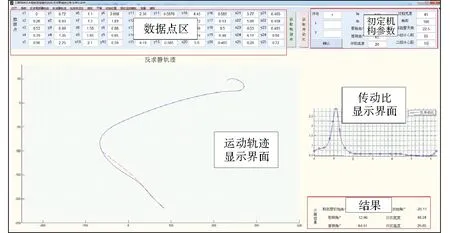
图8 反求辅助设计软件界面Fig.8 Aided software interface of reverse design
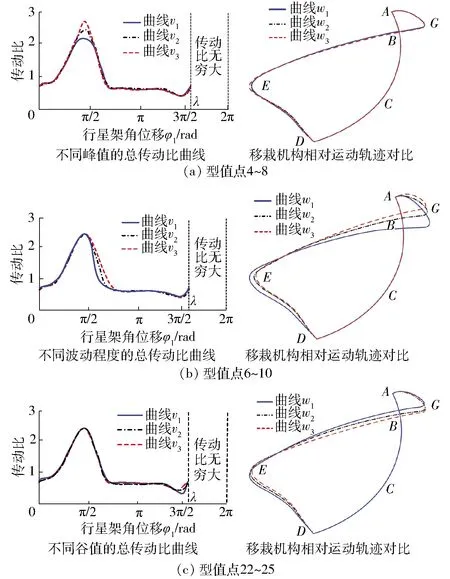
图9 传动比对移栽相对运动轨迹的影响Fig.9 Influence of transmission ratio on transplanting static trajectory
图9a显示,调整传动比曲线的型值点4~8数值使峰值变大时,相对运动轨迹回程段越往左侧偏移(有利于减小绝对运动轨迹回程段前倾程度),BC段轨迹略微下移,对移栽机构的相对运动轨迹右上角环扣形状影响不大。
图9b显示,调整传动比曲线的型值点6~10数值使曲线的波动程度由急到缓时,相对运动轨迹回程段越往右侧偏移(容易发生带苗现象),移栽机构的相对运动轨迹右上角的环扣高度(Hg)增大,取苗点位置降低。
图9c显示,调整传动比曲线的型值点22~25数值使曲线末端谷值变大时,相对运动轨迹回程段越往右侧偏移(容易发生带苗现象),取苗点位置升高,移栽轨迹右上角环扣高度(Hg)、宽度(Hk)变小。
综合上述参数的影响,围绕设计目标,通过人机交互的方式获得一组较优参数:la=119 mm,lb=152 mm,Hg=25.85 mm,Hk=48.24 mm,φQY=12.96°,φTY=64.51°,φ10=-25.11°,φ50=37.19°,lZ=180 mm。在这组参数下求得最终的相对运动轨迹、绝对运动轨迹、传动比曲线及齿轮节曲线如图10所示。理论结果显示,移栽机构绝对运动轨迹回程段位于秧苗位置竖直线左侧,导入CAD软件测得LD′E′>120 mm,与原机构绝对运动轨迹(图1c)相比,本文设计的移栽机构绝对运动轨迹不前倾,且推苗角增大到64.51°,理论上解决了原机构存在的问题。
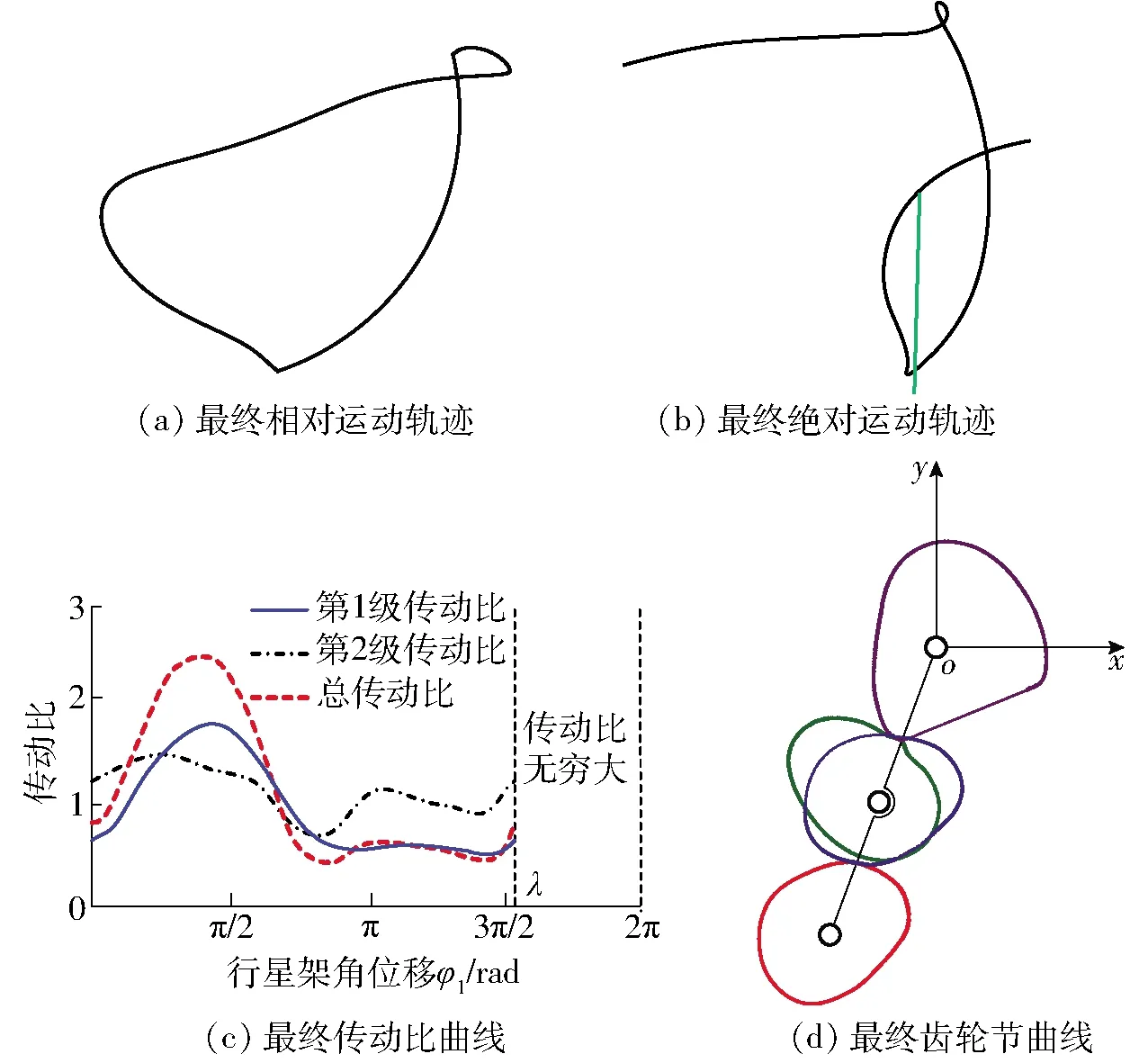
图10 移栽机构最终优化结果Fig.10 Final optimization results of transplanting mechanism
3 移栽机构虚拟仿真
根据反求设计得到满足设计要求的移栽机构各个齿轮节曲线和齿轮相对位置的参数,将各个齿轮节曲线数据导入自主开发的齿廓生成软件[21-23],给定齿轮的齿数,得到各非圆齿轮的齿廓线数据(图11);结合这些数据完成移栽机构的结构设计,运用三维建模软件UG 12.0对该机构各个零件进行三维实体建模和虚拟样机装配,利用ADAMS软件对移栽机构虚拟样机进行了相对运动和绝对运动仿真,绘制出移栽臂尖点的移栽轨迹,如图12所示。
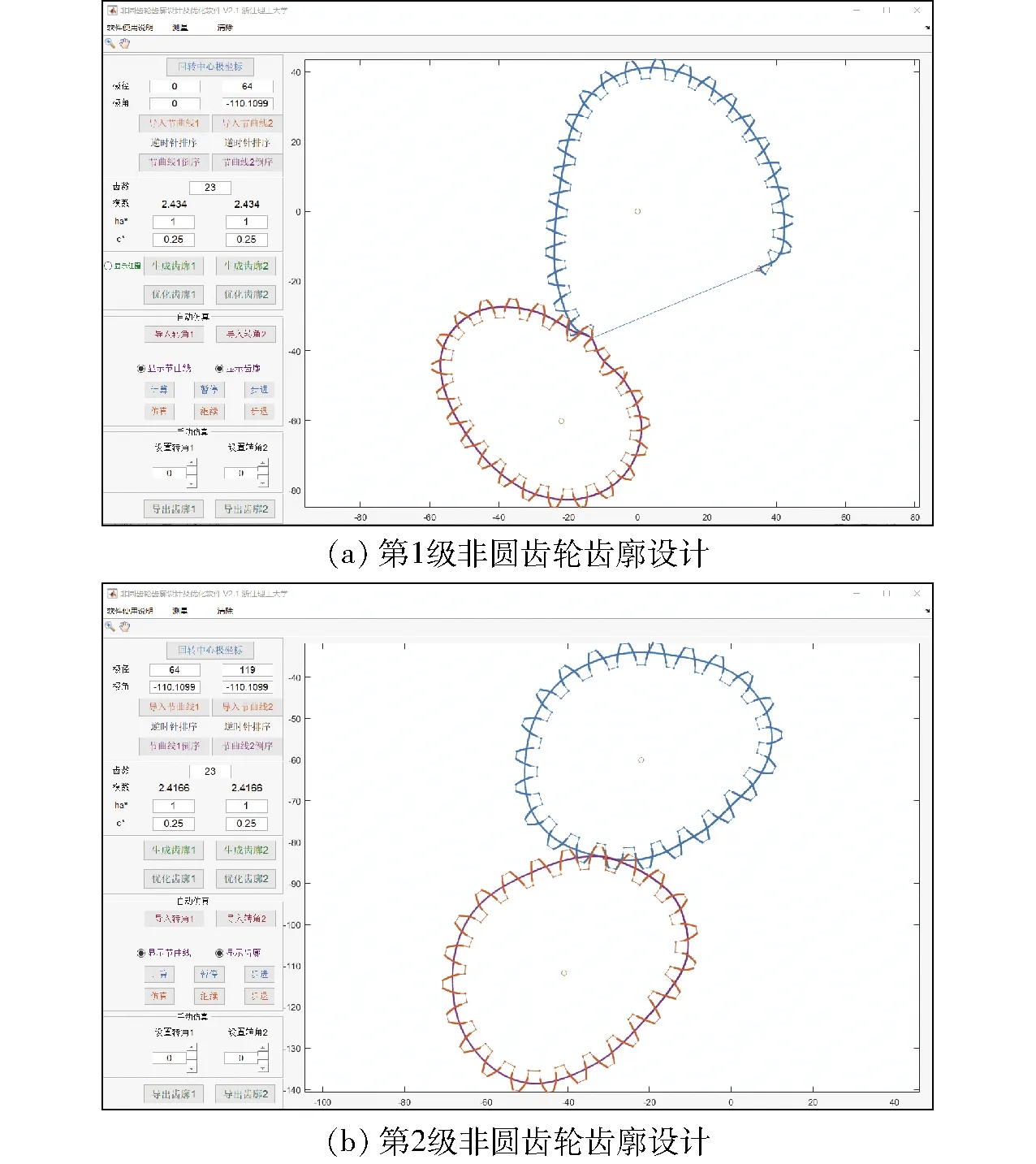
图11 齿廓设计界面Fig.11 Interface of profile design software
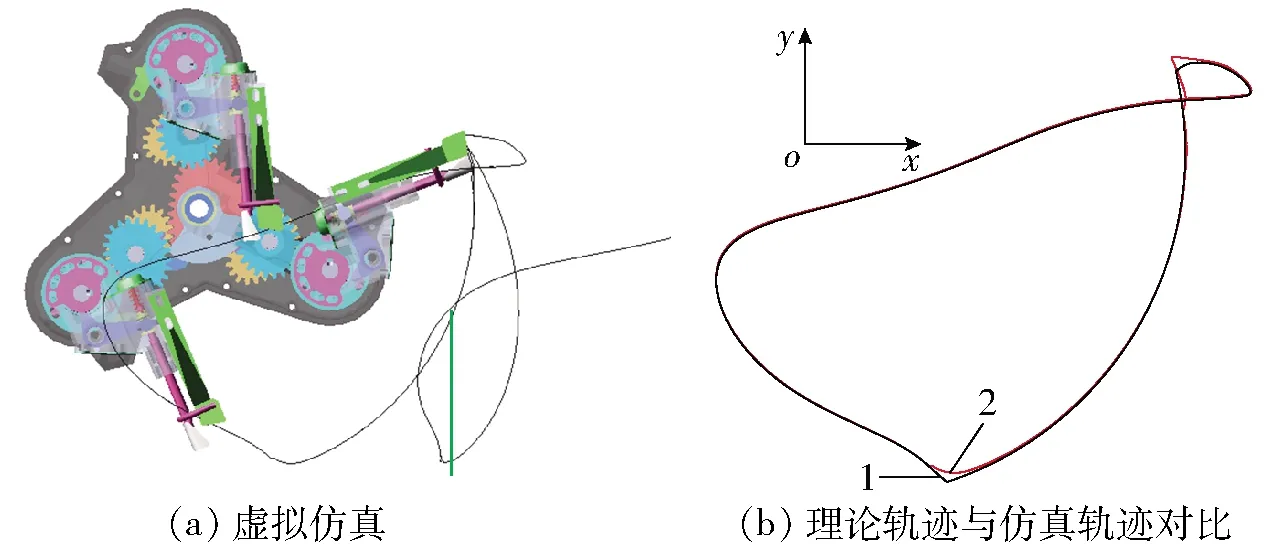
图12 理论轨迹与仿真轨迹对比Fig.12 Comparison between theoretical trajectory and simulation trajectory1.理论计算轨迹 2.虚拟仿真轨迹
由仿真结果可以看出虚拟仿真得到的相对运动轨迹与理论设计得到的相对运动轨迹基本重合,其中环扣部分轨迹不重合,主要原因是设计齿轮脱离啮合后,锁止弧的作用代替了被切除齿的传动,对齿轮起到了导向作用;轨迹下端部分轨迹不重合,主要原因是齿轮进入啮合前,缓冲弧的作用使得移栽臂提前发生了转动。此外,绝对运动轨迹回程段位于秧苗位置竖直线左侧,导入CAD软件测得LD′E′>120 mm,即绝对运动轨迹回程段不前倾,虚拟样机推秧角约63.34°,理论上验证了所设计机构解决了原机构绝对运动轨迹回程段前倾和推秧角偏小的问题。
4 样机试验
为了进一步验证反求设计方法正确性及所设计的移栽机构满足设计要求,研制了移栽机构物理样机,搭建了水稻钵苗移栽机构运动学试验平台(图13a),并完成了轨迹与位姿验证试验和推苗试验。在进行轨迹验证时,设置移栽机构转速在60 r/min左右,采用高速摄影技术及Blaster’s MAS图像分析软件分析移栽机构在运转时移栽臂夹苗片尖点的相对运动轨迹。在进行位姿验证时,采用DMI410数显倾角仪测量3个移栽臂在取苗和推苗位置时的姿态角(图14),分别测量3组并分别计算推苗角和取苗角的角度差(简称取推苗角度差)。此外,开展了土槽试验台上的推苗效果试验,如图15所示。

图13 水稻钵苗移栽机构试验台与钵苗Fig.13 Test bench of rice seedling transplanting mechanism and rice seedling

图14 取苗、推苗角测量Fig.14 Measurement of taking-seedling and pushing-seedling angles

图15 推苗试验Fig.15 Tests of pushing-seedling
移栽机构轨迹高速摄影结果如图16所示,移栽机构3个移栽臂的取苗角、推苗角、角度差实际测量结果如表1所示,并与理论计算、ADAMS虚拟样机仿真结果及设计目标进行了对比。

图16 移栽机构试验轨迹Fig.16 Test trajectory of transplanting mechanism
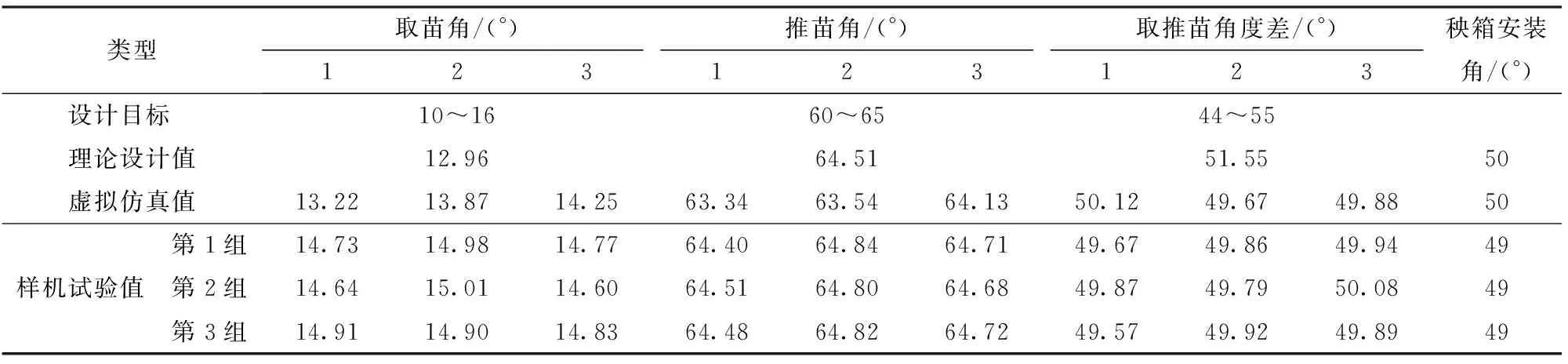
表1 移栽机构设计结果对比Tab.1 Comparison of transplanting mechanism design results
比较理论计算、虚拟样机仿真、高速摄影试验得到的相对运动轨迹结果,可以看出轨迹基本一致,在株距(移栽机前进速度相同)和行星架转速相同情况下,相对运动轨迹相同,则其绝对运动轨迹必相同。因此,根据理论计算、虚拟仿真及高速摄影试验中相对运动轨迹基本一致,可间接验证其实际作业与理论计算、虚拟仿真得到的绝对运动轨迹基本一致,即绝对运动轨迹回程段位于秧苗位置竖直线左侧,LD′E′>120 mm,解决了绝对运动轨迹前倾问题。由表1可知,同一组的3个移栽臂实际测量的取苗角、推苗角以及3个移栽臂的3组实际测量的取苗角、推苗角存在误差,误差均在1°以内,其主要原因是非圆齿轮加工和装配存在误差,导致啮合时产生微小侧隙。但3个移栽臂取苗角、推苗角均在设计目标范围内,验证了设计的合理性和有效性。与前期研发的3臂水稻钵苗移栽机构[12]相比,本文所设计的移栽机构的推苗角提高了9.08°以上,取推苗角度差与秧箱实际安装角误差在-2°~2°范围内,解决了推苗角偏小的问题。
5 结论
(1)针对前期研发的三移栽臂水稻钵苗移栽机构应用中存在的问题,建立基于局部运动轨迹的反求设计模型,开发了基于Matlab的反求设计辅助分析软件,通过人机交互的方式获得一组满足设计要求的结构参数和相应参数下的运动轨迹,完成了三臂回转式水稻钵苗移栽机构改进设计。
(2)搭建了运动学试验平台开展高速摄影试验,通过比较理论计算、ADAMS虚拟样机仿真与高速摄影试验得到的相对运动轨迹,得出了理论轨迹、虚拟仿真轨迹和实际运动轨迹基本一致的结论,验证了移栽机构反求设计的正确性。
(3)通过分析理论设计、虚拟样机仿真的结果,可知绝对运动轨迹回程段D′E′高度LD′E′>120 mm、3个移栽臂实际推苗角(误差相差在1°以内)相对原机构提高了9.08°以上,取推苗角度差与秧箱实际安装角误差在±2°以内,证明所设计机构解决了原机构移栽绝对运动轨迹前倾和推苗角偏小的问题,同时表明了移栽机构推苗直立度得以改善。
