基于特征提取的地形渲染增强方法

刘思成，蒋志强

（四川大学 计算机学院，四川 成都 610065）

近年来，随着计算机软件与硬件水平的提高，特别是GPU 处理性能的显著提高，在三维地球仿真领域，人们对于数字地形地貌渲染的细节要求越来越高。在地形仿真中，通常采用高精细度的数字高程模型（Digital Elevation Model）结合卫星影像贴图的方法对地球进行仿真，精度越高的卫星贴图与数字高程越能提高最终的渲染效果。然而，高清卫星影像贴图需求的存储空间极大，加载高清的卫星影像对计算机硬件有更高的要求，高精度的影像卫片以TB 为存储单位，过于精细的影像卫片在加载速度、实时性上难以满足三维仿真场景的需求。此外，通过数字高程模型和卫星影像组合的方式所展示的地形地貌无法清晰、准确地呈现，如山脊、山谷等复杂的地貌，损失相关地形细节。在进行地形地貌相关方面的研究时，多数研究重点放在数字高程的加载以及地形的曲面细分，例如王宇等[1]提出加载地形的细化算法。此外通常采用地形晕渲技术对地理特征进行提取，然后进行着色处理，例如胡丹丹等[2]提出的数字地貌晕渲的特征增强。但上述方法通常对于三维地形的实际渲染效果提升有限，特别是在数字高程与卫星影像贴图结合时难以清晰直观地展示地势的起伏。

为此本文提出了一种基于提取地形特征的地形增强方法。通过特征提取算法实时提取出山脊、山谷等地貌特征，再通过着色器结合实时光照与法线在原有卫星影像基础上进行融合，从而达到以较小的性能代价来增强地形地貌特征的效果，使得地形更加具有层次感，保留更多的地形细节。

1 相关理论与算法

1.1 数字高程模型

在进行三维地形渲染需要用到相应的地形数据，地形数据通常是以二维结构储存，是带有空间位置特征和地形属性特征的数字描述。目前较为常用的做法是采用数字高程模型[3]。数字高程模型是一种储存了地形表面高度数据的几何模型，同时还存储了对应的地理位置信息。通过数字高程模型可以计算出地形的坡向、坡度等数据。

数字高程模型按照数据组织表达形式分类，其中常见的主要有两类：规则矩形格网和不规则三角网，如图1 所示。

图1 数字高程模型

规则网格通常是使用相同的三角形、正方形、矩形等图元将空间区域切割为规则的格栅单元，其中每一个切割出来的单元对应一个点位的高度数据，在格栅间隔较大时容易丢失地形细节，比如山川的起伏、河流分布，但规则网格制作简单使用方便，是较为通用的做法。不规则网格是使用有限个采样点获取离散数据，将这些离散点通过一定的规则组合成连续的三角面，能够很好地反映地形细节，构建过程复杂，且使用时需要花费大量时间去处理各个三角面之间的位置关系，因此本文为了高效地进行三维地形可视化采用了以规则网格为组织形式的数字高程模型。

综合本文需求，选取90 M 分辨率的数字高程模型进行研究。

1.2 特征提取区域

地形特征点指地表上各类刚性物体起伏所组成独特性象征和标志，主要包括山顶点（peak）、凹陷点（pit）、脊点（ridge）、谷点（channel）、鞍点（pass），平地点（plane）等6 种，见表1。

表1 地形特征点

山脊是由两个坡向相反坡度不一的斜坡相遇组合而成条形脊状延伸的凸形地貌形态。山脊线是由地形的最高点连线而成，山脊线能够很好地反映出山脉的整体走势。山脊线的数学描述[4]为：设D1 为正向上升类型的反向斜坡，D2 为负向下降类型的反向斜坡，设地面任意一点为P，点P 的高程为Hp，设它们的交线R=D1∩D2，若存在点P∈R，使得对于任意一点I∈R，都有Hp-Hi>0，则称R 为山脊线，D=D1∪D2 为山脊。

山谷是指地貌中等高线的弯曲部分向高处凸出处。山谷线与山脊线相反，地形中最低点的连线称为山谷线。山谷线的数学描述[4]为：设D1 为正向上升类型的反向斜坡，D2 为负向下降类型的反向斜坡，设地面任意一点为P，点P 的高程为Hp，设它们的交线R=D1∩D2，若存在点P∈R，使得对于任意一点I∈R，都有Hp-Hi＜0，则称R 为山谷线，D=D1∪D2 为山谷。

在地形特征提取的相关研究中，通常着重处理山脊线和山谷线，这两类特征辨识度高效果明显，对于突出地势起伏有着重要作用，而其他的地形特征处理起来复杂，且不易直观显示，因此根据本文的研究需求也同样选择处理山脊线和山谷线这两个地形特征。

1.3 数字地形分析

数字高程模型缺乏普通纸质地图具有的直观性，所含有的地形信息具有一定的隐蔽性。从数据结构上来看，数字高程模型是一组离散的呈规则或不规则三角网的高程数据，其数据本身无法反映地形地貌的特征。因此利用数字高程模型进行地形地貌分析需要一种基于离散数据的信息分析方法，即数字地形分析（Digital Ter-rain Analysis，DTA），定义为在数字高程模型上进行地形属性计算和特征提取的数字信息处理技术，而用于进行地形属性计算的数学模型和地形特征提取算法称为DEM 解译算法（DEM Interpretation Algorithms）[5]。DTA 技术是各种与地形因素相关的空间模拟技术的基础，其结果通常被理解为更为广义上的DTM，即数字地面模型。DEM、DTA、DTM 的关系如图2所示。地形的山脊线、山谷线、河流等地形特征线是整个数字地貌的核心，因此合理地运用数字地形分析从数字高程中提取出地形特征在三维地形渲染和水文分析等方面都具有重要意义。

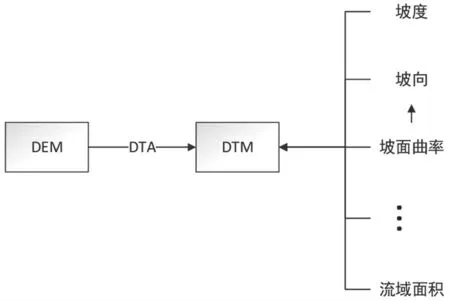
图2 DEM、DTA、DTM 关系图

1.4 法线计算

为了模拟出地形在光照下的阴影以及凹凸不平的效果，传统方法通常根据模型单独计算出一张法线贴图，即保存了法线信息的一组二维数据。而在三维地形渲染中，数字高程模型数据量巨大，单独渲染法线贴图以及处理法线贴图的时间成本过大，因此本文通过着色器实时计算法线（图3）。

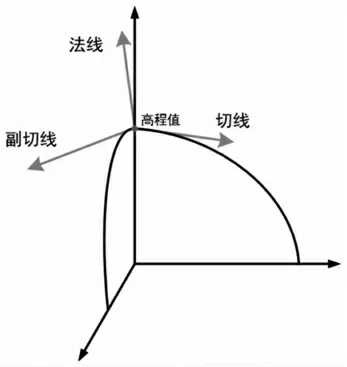
图3 法线计算示意图

2 算法流程

基于特征提取的地形增强算法描述如下：首先通过平面曲率法对数字高程模型进行处理，采用正反地形平面曲率的归一化值作为权重来处理山脊和山谷区域，使其突出显示地形特征区域。然后通过滤波对提取过后的特征进行处理，减少噪点，最后通过着色器计算地形法线调整光照，将提取出的地形特征设置适当的颜色、透明度与卫星影像贴图融合。流程如图4 所示。

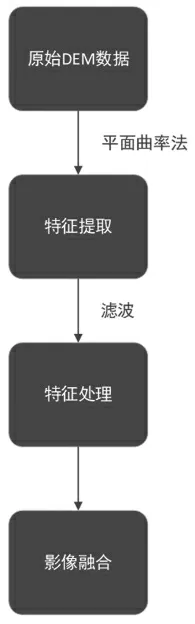
图4 算法流程

2.1 特征提取

目前常见的地形特征提取方法有基于图像处理技术的方法、基于地形表面几何形态分析的方法、流水物理分析相结合的方法以及平面曲率法等。优劣分析见表2。

表2 特征提取方法分析

综上比较，根据本文需要，为了保证着色器实时处理的效率选择采用效率最高、处理最简便的平面曲率法。采用平面曲率法所获取的地形地貌特征线较真实地形的准确度不如基于几何形态与地表流水模拟法，但本文重在反映地形的大致走势，因此可以满足本文的研究需求。

平面曲率是指地形表面上任意一点，用过该点的水平面沿水平方向切地形表面所得到的曲线在该点的曲率值。它描述的是地表曲面沿水平方向的弯曲、变化情况。如果平面曲率为正值，其在水平方向上导数为0且二次偏导数大于0，则栅格属于山脊点；若平面曲率为负值，其在水平方向上导数为0 且二次偏导数小于0，则栅格点属于山谷点。即山脊是平面曲率为正值且在局部区域方向轴上取最大值的区域；山谷是平面曲率为负值且在局部区域方向轴上为最小值的区域。

本文采用平面曲率法提取山脊线、山谷线。地形曲率是指地形曲面在各个界面方向上的形状，凹凸变化的反映，是平面点位的函数。反映了地形结构和形态，在地表过程模拟、水文、土壤等领域有着重要的应用价值和意义。

平面曲率又称水平凸度，是等高线的方向变化率，可以反映地形的高低起伏[6]。当平面曲率点大于0时为山脊线点，小于0 时为山谷线点，通过计算得到山脊线点、山谷线点连接起来即可得到相应的山脊线、山谷线。

假设地形表面S 的曲面方程z=f（x，y），点P 为曲面S 上任意一点，将曲面S：z=f（x，y）的各阶偏导数用下列符号代替：

根据平面曲率的推导过程及其数学意义，曲面S与XOY 水平面相交线在P 点处的二阶导数即是平面曲率，计算公式如下：

提取结果如图5 所示。

图5 处理效果对比图

2.2 特征处理

根据平面曲率法获取的地形特征数据有大量噪点，因此通过过滤来进行处理。

地形特征提取后获得的是一组二维数据，因此对这组数据的处理，本文采用图像滤波的方法。常见的图像滤波方法如下：

（1）均值滤波[7]，也称为线性滤波，属于低通滤波。具体流程是选取一个大小适当的n*n 的模板，采样这个模板中的每一个点，取其平均值作为该点的像素值。这种方法简单易懂，但不能彻底去除噪点，同时还会降低图像的清晰度。

（2）中值滤波[8]是一种非线性滤波，具体流程是选取一个大小适当的n*n 的模板，采样这个模板中的每一个点，取其中间值作为该点的像素值。这种方法对于校验噪声有着显著的效果，但是对图像的破坏较大，易出现大量断裂，导致图像不连续，且无法处理图像中存在的跳跃变化。

（3）高斯滤波是一种线性平滑滤波，属于低通滤波。具体流程是选取一个大小适当的n*n 的模板，采样这个模板中的每一个点，并计算模板内每一个加权平均值，用得到的值去替代该点的像素值，该方法能够最大程度地保留图像的总体灰度分布。

对比几种滤波方法，通过平面曲率提取出的地形特征数据存在大量的噪声，而提取出的地形地貌特征通常属于高频分量，因此在对初步提取出的地形特征数据处理中，应采用低通滤波进行处理。考虑到滤波时计算效率以及本文对于地形特征提取的精度要求不高。本文采用3*3 模板的均值滤波进行处理。结果如图6 所示。

图6 过滤效果对比图

2.3 卫星影像融合

通过前面章节提取出的地形特征经过处理后与卫星影像进行融合，同时实时计算法线使地形与太阳光所生成的阴影更加立体、真实，可以以较小的性能开销获得较大的地形地貌特征细节的提升。首先着色器（shader）读取地形高程，通过平面曲率法提取出地形特征，然后通过滤波再处理得到过滤后的地形特征，再为地形特征中的山脊、山谷设定适当的颜色和透明度（本文将山脊颜色设定为白色，透明度0.6，山谷设定为黑色，透明度0.2），得到最终的地形特征图，设置光线参数，再根据计算出的法线将地形特征图与卫星影像混合后输出到数字高程模型上。通过透明度适当的曲率混合在卫星影像地图上增加三维地形的整体立体感，同时能够较好地显示山脊山谷的特征，展示地势起伏。如图7 所示。

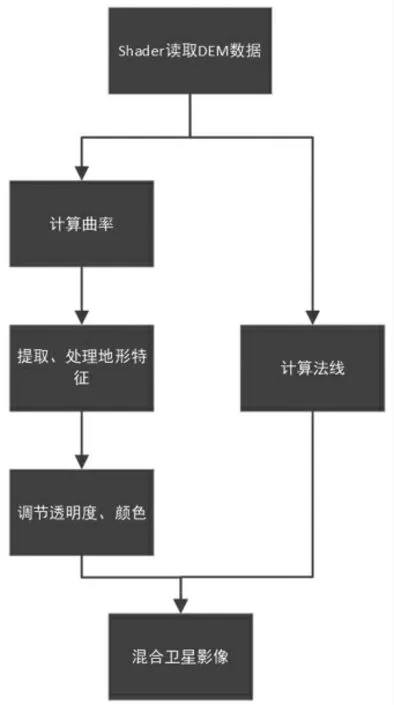
图7 融合流程图

核心代码如下：

3 结果与分析

仿真实验相关参数见表3。

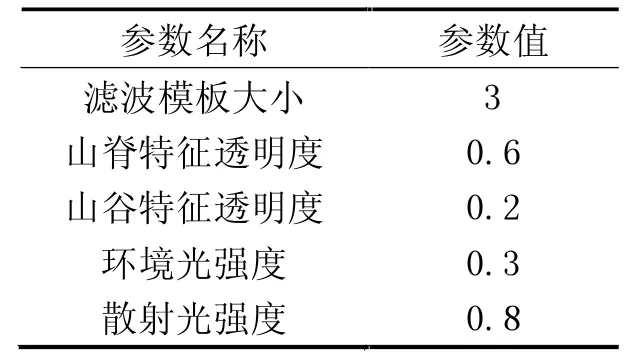
表3 算法参数

渲染效果对比如图8 所示。

图8 渲染效果对比

关闭垂直同步后在三维地球中进行漫游实时帧率，如图9 所示。

图9 实时帧率对比

运行1 000 s 平均帧率，结果如图10 所示。

图10 帧率对比

从对比图中可以看到通过提取地形特征进行加强过后的三维地形效果有了显著提升，相比原始卫星影像地形的立体感提高了很多，其次地势起伏、高低落差更加明显，有利于准确展示地形地貌的细节。在渲染效率方面影响较小。

4 结束语

开启地形增强后对于整个系统的效率影响较小，但对整体的地形仿真效果有了很大提升，通过此方法提取的地形特征适用于提高地形渲染效果，对展示地形地势起伏有较大作用，提高了地形的立体感，对于作战指挥或是地理信息展示具有重要意义。目前本方法着重对山脊、山谷进行了强化，对于其他的地形特征表现的准确度和细节保留程度还有提高的空间，其次选取滤波方法取决于如何平衡效率与渲染效果，本文选择了较为简单高效的滤波方法，但是过滤效果比较一般，此外针对不同地区所需的特征线透明度、颜色等参数设置还有待进一步研究。