社区快递智能柜选址布局研究与应用

王亚如，陈 超

（辽宁工业大学 经济管理学院，辽宁 锦州 121001）

随着社会经济的疾速发展，电子商务信息技术的研讨开发和推行，消费程度的不断提高，快递效能的末端服务成为了人们关注的焦点。末端服务的时间成本、准确度、安全性和快捷性是快递业服务质量的关键因素，社区物流是末端服务中必不能少的一部分，智能柜合理的选址直接关系到客户对快递业服务的满意度，决定着快递业的发展。丁猛以网点数量最小和固定网点数量的选址模型来解决需求量与取件距离之和最短的问题，并提出大学校园智能快递柜备选网点的选择方法。张西莎等对YSL 社区快递柜的网点分布不均问题，首先采用集合覆盖模型建模，求出选择方案，再采用层次分析法对可选方案分析建模。檀竹隔对合肥工业大学实证区域调研，建立集合覆盖模型与层次分析法两级优化模型，对快递自提柜选址模型的合理性和实用性进行实证分析。黄凤春结合生活实际需要，运用POS 算法得出了模型最优解，助力了快递公司智能快递柜的收益最大化目标的实现。

1 研究方法

1.1 重心法

该方法通常被应用在物流运输领域，指的是一种设置单个仓库和厂房的方法，其主要考虑运输货物量、现有的分销仓库等，目的将仓库或厂房设置在离主仓较近的位置，通过缩短运输路程来尽量降低运输费用，从而帮助企业实现利益最大化的目标。该方法的计算公式为：

式中，X0与Y0分别代表重心位置的横纵坐标，待确定的重心位置的坐标即为（X0，Y0），各个需求地的坐标为（xi，yi），mi代表每个需求地的需求量。

1.2 免疫优化算法

免疫优化算法常用于物流行业，具体可以用于物流仓库的选址，从而降低运输成本与仓储成本。因此本文在建立智能柜选址模型后，引入免疫优化算法完成求解，验证选址方案的合理性，并得到相应的成本预算。

2 智能柜选址模型构建

2.1 条件假设

假设一：配送网点总容量可满足顾客需求，配送辐射范围需求量确定。

假设二：一个需求点仅由一个智能柜中心供应。

假设三：不考虑配送点到智能柜的运输费用。

2.2 构建模型

该选址模型需满足距离要求，并从n 个需求点找出智能柜，迎合n 个需求点储存物品的需求。其目标函数为：

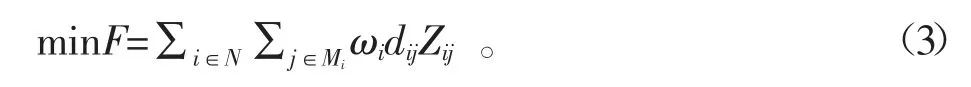
约束条件为：

其中，N={1，2，…，n}是所有需求点的序号集合；Mi为到需求点i 的距离小于s 的备选智能柜集合，i∈N，Mi⊆N；ωi为需求点的需求量；dij代表从需求点i 到离它最近的智能柜j 的距离；Zij为[0，1]变量，代表物流中心与用户之间服务需求的分配关系，当Zij=1 时，代表由智能柜j 供应满足需求点i 的需求量；否则Zij=0；hj为[0，1]变量，当hj=1 时，表示智能柜储存点选取j 是合理的；s代表智能柜与需求点的距离上限。

式（4）保证每个需求点只能由一个智能柜储存点服务；式（5）确保需求点的需求量只能被设为该智能柜供应；式（6）规定了被选为智能柜的数量为p；式（7）表示变量Zij和hi是[0，1]变量；式（8）保证了需求点在智能柜储存的范围内。

2.3 计算步骤

第一步，抗原识别，即分析实际问题之后建立目标函数，设立约束方程。

第二步，得到初始方程解，即确定初始选址方案。

第三步，计算抗体亲和度，其公式为：

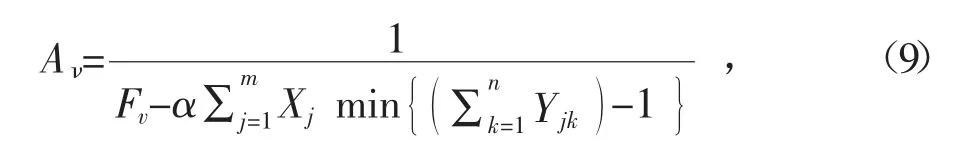
式（9）中，Aν表示亲和度，Fv表示目标函数，代表基于距离的惩罚值，若得到的结果较大代表备选中心与需求点距离过大，为了保证其适用性，需要降低其被选中的概率。

第四步，判断是否满足终止条件，即计算结果符合终止条件或迭代次数，则可直接输出结果，反之，需要调整变量值继续计算。

第五步，抗体群多样性评价，即利用该公式：

计算其抗体浓度与亲和度，浓度过高则证明抗体有效，可直接消灭抗原，但并不是浓度值越大越好。

式（10）中，Cv表示抗体浓度，M 为种群中抗体总数，Xij为[0，1]变量。

式（11）表示如果抗体i 与抗体j 的相似程度大于设定的阈值T，则记Xij为1，反之为0。

繁殖概率计算公式如下：

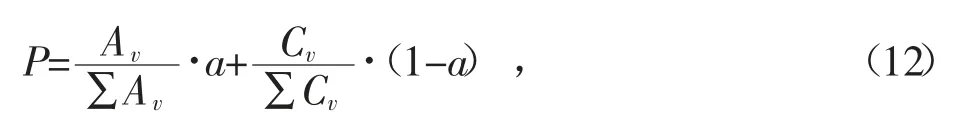
式（12）中，P 表示个体繁殖率，Av表示抗体的亲和度，Cv表示抗体的浓度，a 表示多样性评价参数。根据个体繁殖率进行排序，选取排名靠前的抗体形成父代群，更新记忆库。

第六步，免疫操作，包括免疫的选择、交叉、变异。

第七步，更新种群，得出结论。即保留亲和度较好的个体，将个体繁殖率较低的抗体替换为经变异操作新生成的抗体。

3 实例研究

小区总占地面积5.28 万m2，总建筑面积26.82 万m2，住宅面积18.99 万m2。小区共17 栋住宅8 栋小高层（包含1栋物业楼）和9 栋高层组成，具体户型图如图1 所示。为了营建一个自然谐和的宜居环境，结合自然与人文的小区设有隔音屏、绿化带，高达30%的绿化率。园区内有高档休闲会所与780 m2大型幼儿园以及地下车库。

图1 社区户型图

通过表1 可以看出每栋楼的住户数量，并根据统计学原理可知，每栋楼的快递需求量大体相似，因此假设每户在同一时间范围内取件数量为1，则可用住户数量代替快递需求量。

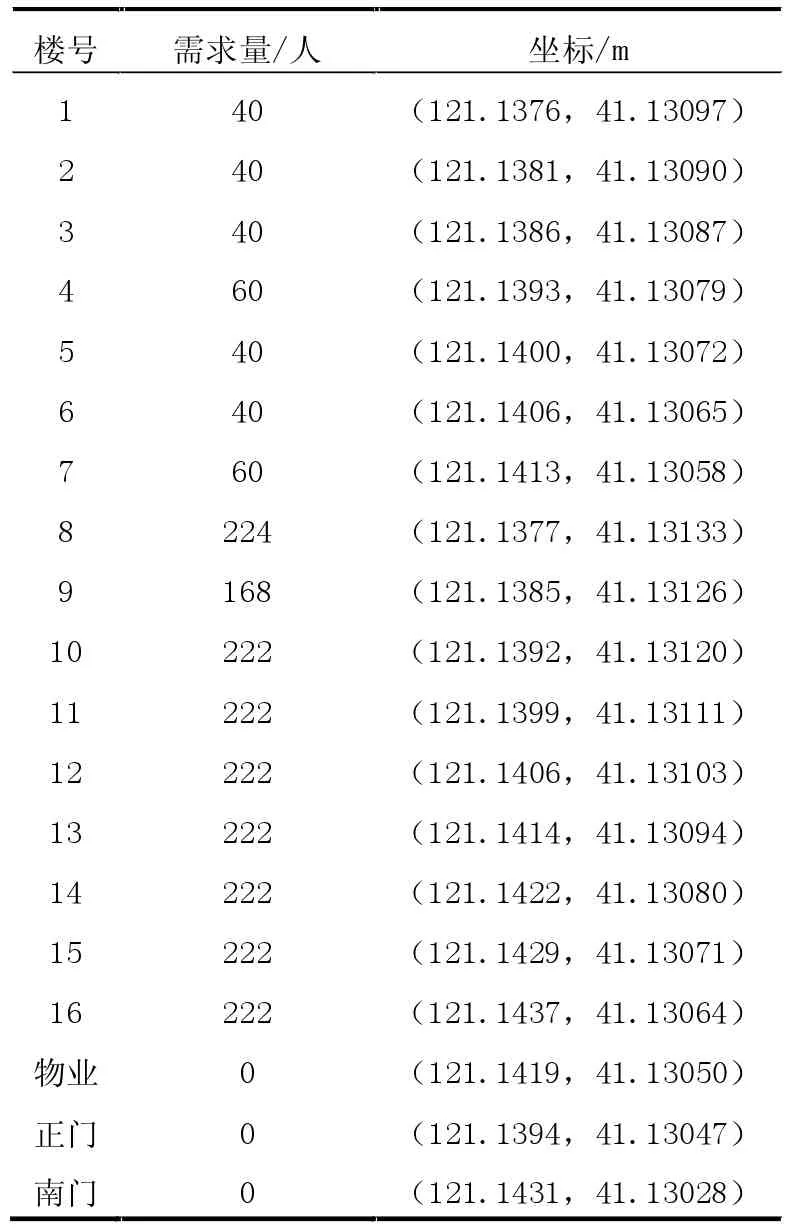
表1 需求量与坐标基本情况

3.1 基于重心法进行初步选址

首先构建参照坐标，为了简便起见，将该社区的地理坐标作为参照坐标，相关参数参考该小区总平面规划图，并作处理，社区坐标分布图如图2 所示。

图2 社区坐标分布图

利用重心法模型的计算公式，将表中的数据代入公式（1）、公式（2），得X0=121.1406，Y0=41.13065。故重心坐标为（121.1406，41.13065），如表1 中6 号楼坐标所示。

采用重心法纵然可以得到模型中的理论选址地点，但考虑实际中的经济成本、取件空间等诸多因素，因此该坐标只能作为参考，还需在附近选取几个备选地址。根据本研究首先将选址地点统一罗列出来作为备选，其次根据居民区实际情况运用免疫算法对备选方案进行计算与决策。经实地考察，得到3 种备选方案：分别是重心点的6 号楼，及根据三角形稳定性实地距离测量选中的11 号楼和15 号楼。

3.2 基于免疫优化算法模型求解

利用MATLAB R2015b 软件，通过对参数的多次调试，最终设置种群规模为10，记忆库容量为10，最大迭代次数为50，交叉概率为0.5，变异概率为0.4，多样性评价参数为0.95，参数设定之后输入小区中各物流节点的坐标、建设及经营成本、进出货情况等各项数据，通过多次迭代计算后，得出的免疫算法收敛曲线如图3 所示。

从图3 中可以看出，在12 次迭代时抗体适应度值不再发生大范围变化，而是趋于范围性稳定，证明免疫优化算法在得到最优解的同时，其达到收敛的时间也比较短，能够有效解决实际配送问题，并满足居民需求。

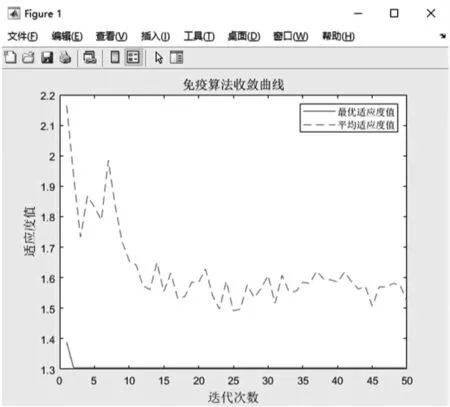
图3 免疫算法收敛曲线

为了更加直观地看出选址情况，特将经纬度转换为通俗易懂的大地坐标，一方面可精确计算各地址之间的距离间隔，另一方面能够清楚地观察到配送中心位置与配送情况。如图4 所示为物流配送中心分布及其负责的配送服务情况，方框选定的圆点代表选择建设物流配送中心的楼号，其负责配送的需求点以细线的形式连接起来。

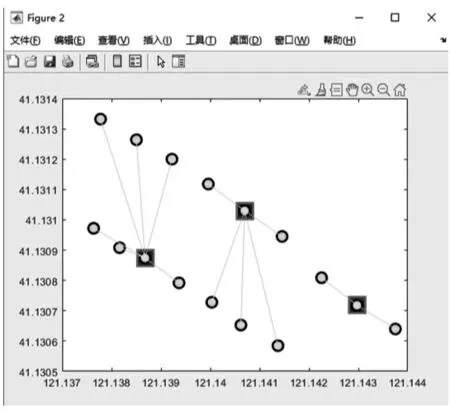
图4 智能柜选定及其配送情况

3.3 选址结论

通过免疫优化算法计算得到的最优解为5 号楼，12 号楼，15 号楼。结合重心法，根据实地考察小区的实际空间，5 号楼和6 号楼之间是休息凉亭，其为智能柜建造提供了有利条件；11 号楼和12 号楼之间是车辆、居民出行道路，符合智能柜的选址条件；15 号楼有个小型超市并且是南门出入口，符合智能柜选址条件。

4 结束语

综上所述，在充分考虑解决实际问题的基础上，引入了重心法与免疫优化算法，通过结合实例最终选定了该小区的智能柜位置，对促进居民的生活便利性与提高物流配送效率均有重要意义。随着互联网技术的持续升级与应用，快递业务日渐倍增，解决最后1 km 的配送问题才是突破行业瓶颈的有效途径，精准的智能柜选址是提升居民取件便利性与企业效益的最佳选择。