超短脉冲激光与碳化硅相互作用研究

王金舵

（光学辐射重点实验室，北京 100854）

碳化硅（SiC）因其良好的材料性能被广泛应用于半导体制造行业[1-3]、航空航天领域[4-6]。碳化硅的切削性极差，易造成刀具产生红热性，需采用金刚石材质刀具[7]，而激光加工则不存在上述问题。长期以来，人们开展了大量关于激光与碳化硅相互作用的研究。研究表明[8-10]，相较于连续激光、长脉冲激光甚至纳秒级的短脉冲激光，皮秒至飞秒级的超短脉冲在加工时，热效应作用机理逐渐被场效应作用机理所替代。当脉宽减小到10 ps 以下时，由于脉宽小于电子晶格的热弛豫时间，电子吸收激光光子能量后，这些能量无法通过声子作用传递到晶格，从而不会发生晶格间的热传递现象，也就是说不产生热现象或仅产生局部有限的热现象，即实现冷加工。2010 年，哈尔滨工业大学的赵清亮等[11]人开展了飞秒激光加工SiC 烧蚀阈值及材料去除机理的研究，研究了脉冲数目、重复频率和入射激光功率对加工微结构形貌的影响规律。2016 年，天津工业大学的李晓宇等[12]人开展了飞秒激光加工SiC 的作用机理与激光功率密度阈值、脉冲宽度、频率、重叠率等参数关系的研究。2021 年，吉林大学的徐思佳等[13]人开展了基于水辅助的飞秒激光SiC 微孔加工方法的研究。在激光与物质的相互作用中，损伤阈值是最为重要的参数，根据损伤阈值可以在激光加工时精确估算所需能耗，提高效率节约成本。通常情况下，损伤阈值可由实验测量或依据经验公式计算得到[14]。本文将基于电子密度增长速率方程，结合雪崩电离模型、光致电离模型及电子空穴复合模型，对百飞秒到十皮秒量级的超短脉冲与SiC 相互作用过程进行仿真分析，得到SiC 损伤阈值与激光脉宽、波长间的数值关系。

1 理论模型

1.1 电子密度增长速率方程

超短脉冲激光与物质相互作用时主要利用高峰值功率密度或者说同步产生高电场强度，去驱使电子脱离原子束缚，形成自由电子。当自由电子到达一定数量后，在宏观上形成等离子云，在损伤形貌上呈现剥离或消融。因此，可利用电子数密度模型在时域上对不同参数的超短脉冲激光辐照SiC 后自由电子变化情况进行仿真分析[15]。

电子数密度的变化主要由光致电离、雪崩电离及电子空穴复合三种效应决定，其速率方程的表达式为：

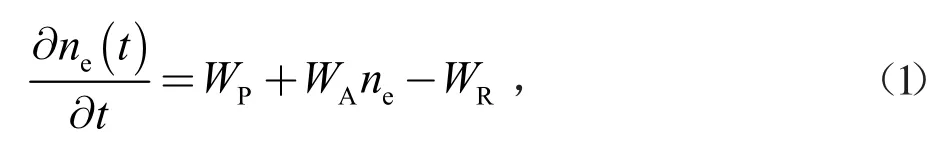
式中，WP为光致电离速率，WA为雪崩电离速率，WR为复合速率。

1.2 光致电离

依据Keldysh 理论[16]，当强激光与物质相互作用，根据电场强度和入射激光频率不同，可将光致电离分为两种情况：多光子吸收电离和光致隧道电离。为了界定这两种情况，Keldysh 提出了固体Keldysh 系数为：

式中，ω 为入射激光的圆频率，m 为电子与空穴约化质量（或载流子的平均有效质量），Eg为有效带隙宽度，e为单位电荷，E 为入射激光的电场强度。在变化的激光电场中，带隙宽度会发生变化，其有效带隙宽度为：

式中，E0为本征带隙宽度。约化质量m 可表示为：

式中，me为电子有效质量，mh为空穴有效质量，不同材料的有效质量与电子的静止质量m0成一定数量关系。

对于γ 较大的入射激光，采用多光子吸收电离模型，其表达式为：

式中，x 为多光子吸收电离时所需要吸收的光子数，可表示为：

式中，ceil 表示向下取整；Ф（z）为Dawson 积分，其表达式为：

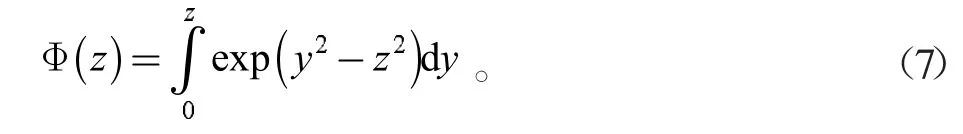
对于γ 较小的入射激光，采用光致隧道电离模型，其表达式为：

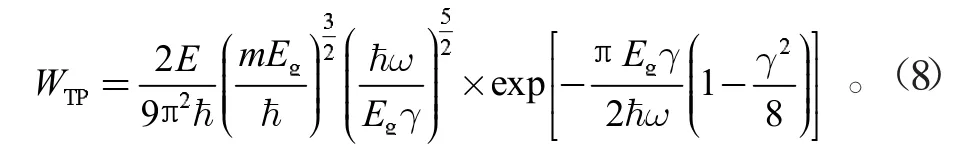
1.3 雪崩电离

雪崩电离又称为碰撞电离，其模型采用直流电场下的雪崩效应。电子通过碰撞将能量通过动能转移，其表达式为：

式中，vd为电子漂移速率，由于聚焦后峰值功率下的激光电场强度一般能达到MV/cm 量级，在此量级的电场强度下，电子漂移速率达到饱和并且与激光电场强度无关。α（E）为一个与入射激光电场强度相关的参数，表达式为：

式中，P（E）为一个电场影响系数，与入射激光电场强度E、碰撞散射电场强度EI、光声散射电场强度EP、热散射电场强度ET相关。本文采用Thornber 雪崩电离模型，该模型适合多种电场强度，其表达式为：

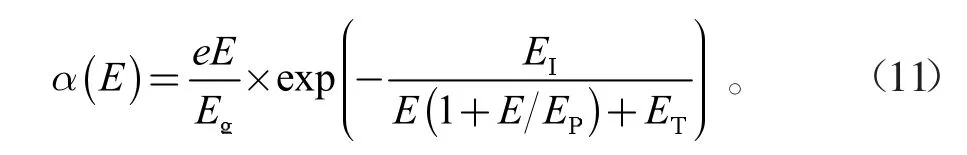
1.4 电子空穴复合

在电离过程中，若未达到临界电子密度，而只形成自由电子，那么电子还是会在一定时间后与空穴发生复合。复合速率与同一时间内自由电子总量有关，可表示为：

式中，ne为电子密度，n0为导带初始电子密度，τ 为复合时间。

1.5 临界电子密度

经过充分电离后的电子密度存在一个临界值，当达到这个值时，形成的等离子云会吸收后续激光能量从而达到宏观上不可逆转的破坏，此时可认为已到达损伤阈值要求。为了减少多余能量产生不必要的热效应，加工激光能量密度应略大于损伤阈值即可。用于表示临界值的临界电子密度表达式为：

式中，ε0为真空介电常数，8.85×10-12F/m。

2 数值计算及分析

2.1 作用过程仿真

SiC 的电子漂移速率为2.5×107cm/s，击穿电场为3～5 MV/cm（取平均值4 MV/cm），相对介电常数为9.7，本征带隙宽度为3.2 eV[3，17]。约化电子质量m≈me，复合时间τ=150 fs，导带中初始电子密度n0为108cm-3量级。高斯型入射激光电场强度可表示为：

式中，μ0为真空磁导率，4π×10-7H/m；ε 为介电常数，是材料相对介电常数与真空介电常数ε0的乘积。

假设入射激光波长为1 064 nm，脉宽tp为5 ps，利用四阶/五阶龙格-库塔算法求解，得到电子数密度随激光脉冲持续时间变化情况，如图1 所示。

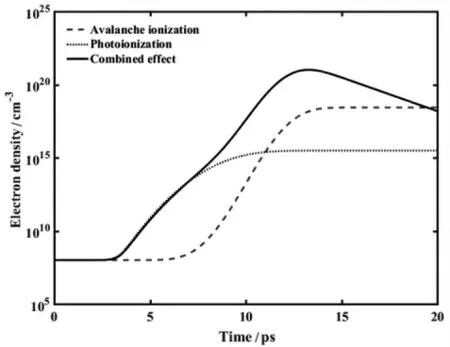
图1 电子数密度随1 064 nm/5ps 脉冲激光作用时间变化曲线

由图1 可知，在激光脉冲作用初期，光致电离对电子数密度的增长起主要作用，增长速率极快后逐渐变缓并趋于稳定。雪崩电离是随着激光脉冲电场的增强而增强，增长速率逐渐增大至脉冲峰值（时间为10 ps）达到最大增长速率，之后增长速率逐渐变缓并趋于稳定，这期间雪崩电离超越光致电离对电子数密度增长起主要作用。电子数密度在～13.4 ps 达到临界电子数密度（～9.9×1020cm-3），之后在电子空穴复合作用下电子数密度逐渐回落。

假设入射激光波长保持不变，脉宽tp缩短为0.5 ps时，电子数密度随激光脉冲持续时间变化情况，如图2所示。

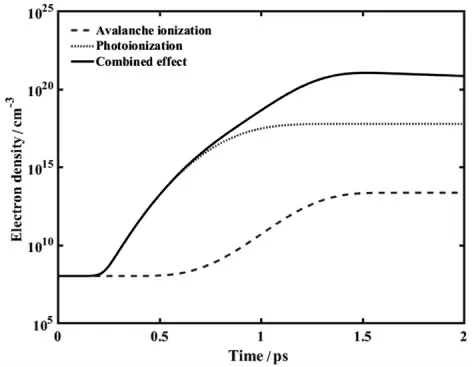
图2 电子数密度随1 064 nm/0.5ps 脉冲激光作用时间变化曲线

由图2 可知，由于脉冲作用时间的缩短，雪崩电离所需电场无法充分发挥其驱动电子作用，整个过程中光致电离对电子数密度增大起主导作用。这种效应随脉宽变窄而越发明显。由于入射激光波长不变，临界电子数密度也不变。电子数密度在～1.5 ps 时达到临界电子数密度。

2.2 脉宽/波长对损伤阈值影响分析

利用基于电子密度增长速率方程的SiC 损伤阈值随激光脉冲作用时间变化模型，计算不同脉宽下1 064 nm 激光辐照下SiC 电子数密度变化情况，得到达到临界电子数密度（～9.9×1020cm-3）所需激光功率密度（损伤阈值），如图3 所示。

由图3 可知，不同脉宽下，SiC 损伤阈值基本呈线性变化，随脉宽变宽而增大。这表明，使用脉宽越窄的激光，加工越容易，但也表明在1 064 nm 单脉冲激光辐照下理论上存在最小损伤阈值，约为0.47 J/cm2。选取几种常见激光波长，计算脉宽为1 ps 时单脉冲激光辐照下SiC 电子数密度随激光波长变化情况，如图4 所示。

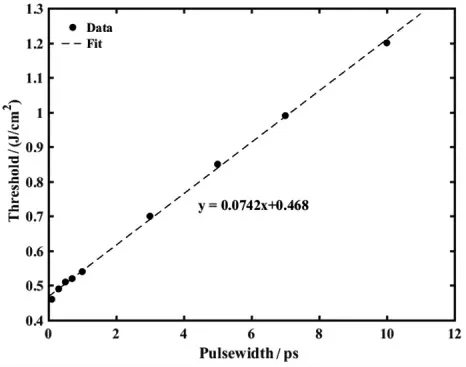
图3 不同脉宽激光辐照下SiC 损伤阈值

由图4 可知，SiC 损伤阈值随辐照激光波长变长而增大，大体上呈线性变化，但存在波长相近情况下，损伤阈值相近甚至相同的情况。这种现象可能与光致电离中，光子能量吸收具有量子特性有关。这种情况在陈洪新等[14]人的飞秒烧蚀SiC 实验中出现过。

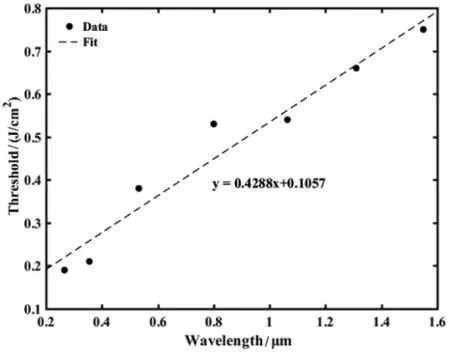
图4 不同波长激光辐照下SiC 损伤阈值

2.3 计算与实验对比

利用本文模型计算不同波长下飞秒激光对SiC 的损伤阈值，激光脉宽设为130 fs，对比参考文献[14]的实验测量结果，见表1。

表1 模型计算结果与参考文献[14]数据对比

由表1 可知，当波长为400 nm、1 550 nm、1 650 nm和1 860 nm 时，模型计算得到的损伤阈值与实验结果较为一致。而波长为800 nm 和1 250 nm 时实验结果阈值偏高，这可能和实验中损伤阈值计算方式与烧蚀面积大小估算相关，得到的烧蚀阈值大于临界损伤阈值。另外，由于SiC 存在多种晶体结构，材料参数存在差异，亦可能导致计算结果与实验结果存在偏差。

3 结论

本文基于电子密度增长速率方程，结合Thornber雪崩电离模型、Keldysh 光致电离模型及电子空穴复合模型，对超短脉冲与SiC 相互作用过程进行时域仿真分析。通过材料损伤与临界电子数密度间关系，得到不同脉宽和波长下SiC 的激光损伤阈值。分析结果表明，在波长不变的情况下，SiC 损伤阈值随着脉宽变窄而减小，基本呈线性变化，且存在理论上的最小损伤阈值。在脉宽不变的情况下，SiC 损伤阈值随波长变长而增大，但存在邻近波长损伤阈值相近甚至相同的情况。将模型计算与文献中实验结果进行比较，具有较好一致性，可为SiC 材料的超短脉冲激光加工参数选择提供理论指导。