基于Midas Civil 的桥梁抗震安全性能验算

韩雨

（中国市政工程中南设计研究总院有限公司，湖北 武汉 430014）

1 工程概况

本文以我国某桥梁工程为例展开分析，该项目设计桥宽为8m，跨径为25m，采用预应力混凝土材料施工，各项技术指标如表1 所示。该桥梁的设计基准期为100年。地勘报告显示建设地场地环境为Ⅱ类，沿线主要为旱地，地表坡度多为6°以下。该项目地处半干旱大陆性季风气候带，气候表现为春季干燥且多风、夏季酷热多雨、秋季温暖凉爽、冬季寒冷漫长，不同季节的气候较为分明。年平均风速约为4.1m/s，雨季主要集中在7、8 月份，雨季降水量约占到全年总降水量的65%～70%。到混凝土、钢束的材料性质[1]，如表3 所示。

表1 项目主要技术指标

表2 端横梁的基本尺寸参数

表3 主要材料性质表

根据设计方案建立简支箱梁的基本模型，并采用SPC 在有限元软件中分别导入梁端截面，并借助软件自动计算各截面对应的形状特性。各截面构造图（以B-B面为例）如图1 所示。

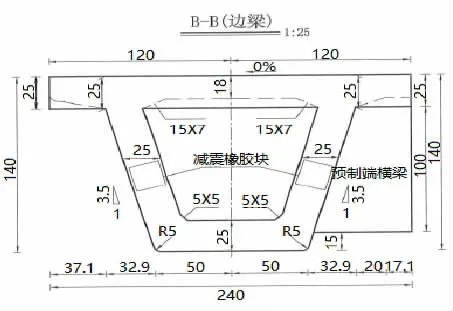
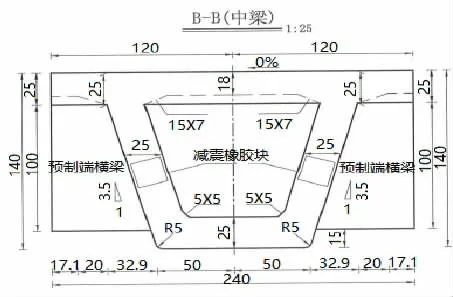
图1 简支箱梁的一般构造图

箱梁之间采取刚接方式进行连接，且在箱梁的横桥向上布置端横梁，其基本尺寸参数如表2 所示。

2 有限元建模

定义材料及截面:

在Midas Civil 软件内分别定义有限元建模所涉及

考虑到混凝土材料在施工、运营过程中可能发生的收缩、徐变等现象[2]，在定义材料时就需要对其特性随时间变化做出假定，以C50 等级的混凝土为例，如表4 所示。

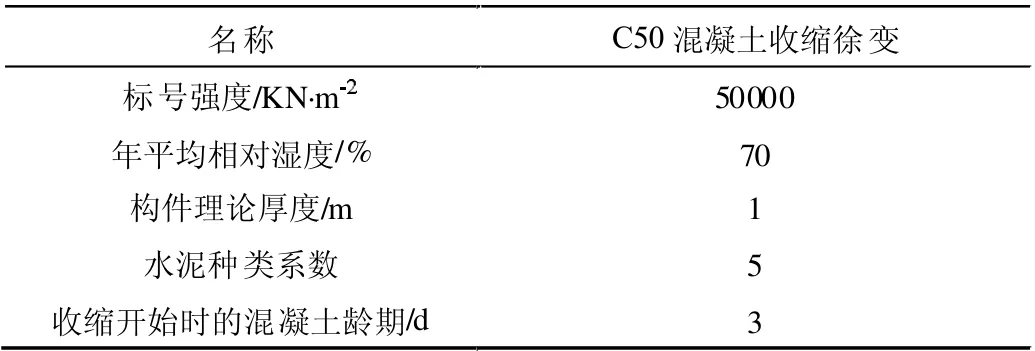
表4 C50 混凝土特性随时间变化

3 输入荷载

在该环节中对静力荷载的工况条件做出定义，其中包括自重荷载、预应力荷载以及铺装施加的二期恒载[3]。

3.1 自重荷载

作为结构抗震计算的重要影响因素，自重荷载需要特别予以重视，在本项目中引入自重系数作为基本参数，分别定义X、Y、Z 向为0、0、-1，以此来转化结构所受的自重荷载。

3.2 钢束预应力荷载

在本项目中结构内共布置有96 条预应力钢束，且均采取两端张拉的方式施加预应力，预应力水平以1370000KN/m2为标准。

3.3 二期荷载

研究表明，铺装工序中所受的二期荷载对于结构刚度影响较为微弱，因此在结构分析时可忽略其对抗震性能的影响。但需要注意的是，应当充分重视其对结构体系质量矩阵的影响。基于施工所用的材料、工艺，计算相应铺装工程量后即可定义二期荷载。

3.4 输入移动荷载数据

移动荷载的定义主要用于模拟桥梁上车辆荷载的作用，沿着车辆行进路线布置荷载来表示车辆行驶的全过程[4]。在这一荷载工况下求得结构内各位置所对应的最大及最小值，为结构设计、验算提供数据支持。

按照表5 中的数据定义双车道线，并完善各车道数据。对结构分别进行竖向基频及特征值分析，得出结构响应的基频为f=3.285047Hz。

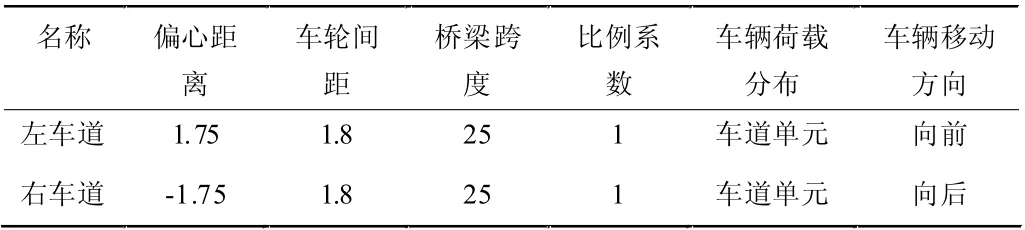
表5 车道数据值

3.5 定义移动荷载工况

在定义移动荷载工况时需要将预先指定好的移动荷载按照一定条件施加到车道上完成分析，这一过程可遵照我国现行规范来确定各车道对应的折减系数。同时可借助Midas Civil 软件基于车道数量自动定义横向折减系数。随后，即可定义子荷载工况条件，按照设计方案分别给出左、右车道的工况。

4 输入反应谱数据

给定某一地震作用，可测得结构体系在该作用下的反应时程曲线，选择反应的最大值，即可视为反应谱曲线上的一个元素点。按照我国现行《公路桥梁抗震细则》即可计算得出水平设计加速度反应谱S：

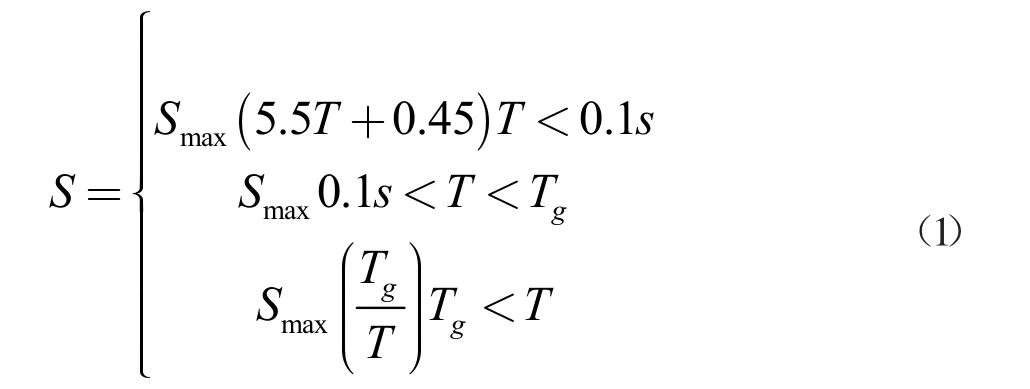
其中，Tg为特征周期，s；T 为自振周期，s；Smax为水平设计加速度反应谱最大值，按照下式求解：

Smax=2.25CiCsCdA

其中，Ci为抗震重要性系数；Cs为场地系数；Cd为阻尼调整系数；A 为水平向设计基本地震加速度峰值。

在本研究中进行抗震设计时，选用振型分解反应谱法进行计算，其在输入荷载时所采用的基本参数如表6所示。

表6 地震荷载参数表

4.1 输入反应谱函数

在有限元分析开始前，首先需要在模型中导入反应谱函数。对于小震作用，一般可采取振型分解反应谱法完成结构的可靠度分析。

4.2 定义特征值

在综合采用振型分解反应谱法及振型叠加法开展结构可靠度分析时，Midas Civil 软件给定了三种不同的分析方式：子空间迭代法、Lanczos 法以及多重Ritz 向量法。考虑到运算效率的影响，在本研究中选定多重Ritz 向量法进行分析，该方法能够更为快速地使得参与质量系数大于90%。在Midas Civil 软件中分别沿X、Y、Z 方向定义10 组加速度，并使其自由叠加，以此得到30 组不同的荷载工况。

4.3 定义反应谱荷载工况

一般而言，在路桥工程设计中仅需考虑水平向地震作用的影响，在本研究中也仅考虑X 向及Y 向的作用，因此在Midas Civil 软件中分别定义顺桥向、横桥向的荷载工况。在组合振型时软件提供了四种不同的方式：

4.3.1 完整二次项组合法(CQC 法)，该方法主要用于振型分布较为密集的结构体系。

4.3.3 ABS 法

ABS 法对不同振型作用下所产生的效应幅值进行叠加求和，考虑到结构各振型的最大值并非同时出现，所以该方法相对保守。

4.3.4 线性法

线性法对不同振型作用下所产生的效应进行叠加求和，同样该法也具有保守的特点。

综合考虑上述各方法的适用范围及特点，最终选用CQC 法进行分析。

5 反应谱分析

5.1 振型及频率

通过Midas Civil 软件分析即可得出结构在地震作用下各模态的振型及频率。借助利兹向量法即可求得结构在地震作用响应的前30 阶振型如表8 所示，其中X、Y、Z 三个方向上振型的参与质量分别为99.35%、99.11%及96.75%，均达到了我国现行规范所要求的90%限值。根据振型分解结果可以发现：振型1、振型2、振型3 及振型4 分别为顺桥向第一阶振型、横桥向第一阶振型、竖向扭转振型及横向扭转振型。

5.2 抗震验算

由于简支梁桥具有结构简单、分布对称的特点，因此在地震作用下结构往往能够保有较好的完整性，即梁体破坏较少，破坏大部分为支座脱落、落梁等。下面主要以桥墩为对象进行抗震设计。

5.2.1 弹性验算

遵照我国现行规范要求，验算地震作用下桥墩结构的抗剪强度、位移是否满足要求。反应谱的验算主要可分为两个不同的阶段，其一为检验桥墩结构在地震作用下是否始终处于弹性状态，因此首先应当按照弹性状态做出验算。

Midas Civil 软件分析发现桥墩结构中有部分位置已经超过了弹性极限，进入塑性状态，难以达到预期承载能力要求。因此，还应当对其塑性状态进行验算。修正参数，使其满足弹塑性分析要求。

5.2.2 弹塑性验算

在弹塑性状态下的有限元分析中，可不对桥墩的强度进行验算。这主要是因为此时桥墩已经超越弹性极限进入到塑性，需要控制的因素为结构变形量，因此只要结构的变形量满足要求即可。在这一阶段中主要以桥墩的抗剪强度、墩顶位移作为分析参数。

通过软件分析，即可得到在地震作用下考虑弹塑性状态桥墩的变形情况，如表7、表8 及表9 所示。

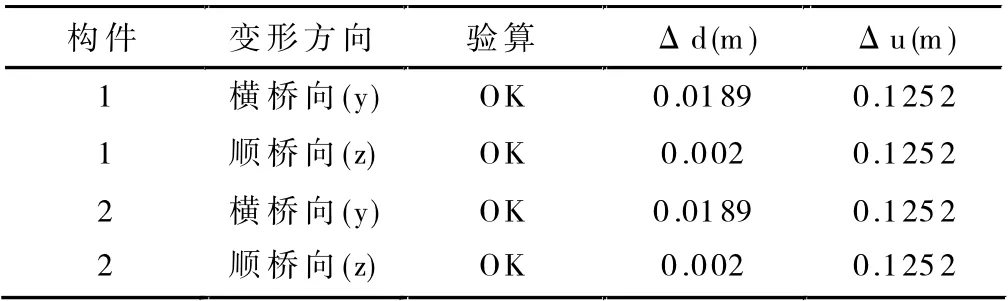
表7 1#墩顶位移验算结果

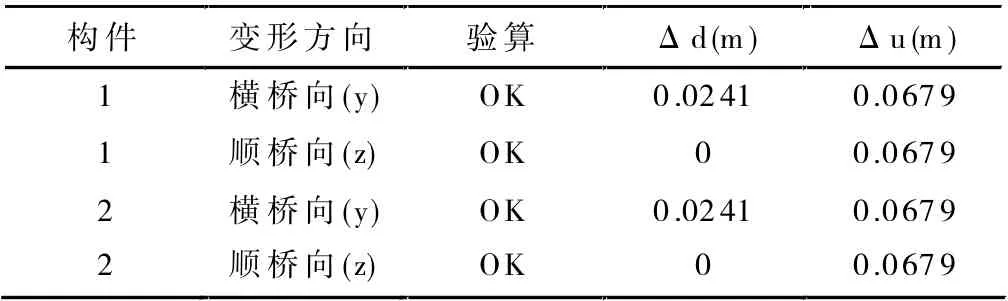
表8 2#墩顶位移验算结果

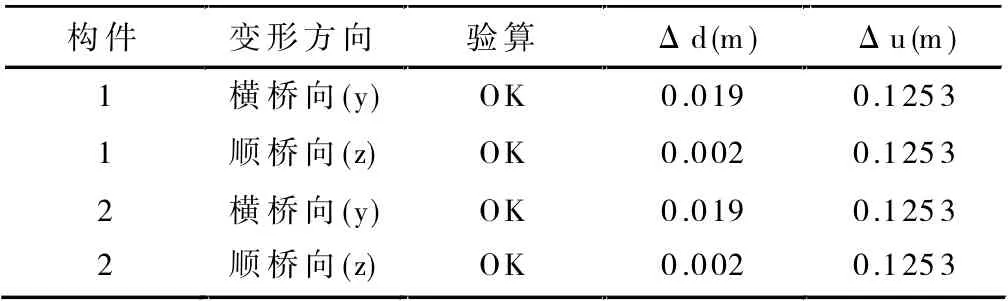
表9 3#墩顶位移验算结果

其中，Δd 为地震作用下考虑弹塑性状态墩顶的位移（m)；Δu 为地震作用下考虑弹塑性状态墩柱的容许位移。根据上表中的数据可以发现，1#、2#、3# 桥墩在地震作用下的位移均能满足预期要求。通过Midas Civil 软件的后处理模块查看塑性铰区的抗剪强度，发现在地震作用下1#、2#、3# 桥墩的塑性铰区抗剪强度均满足预期要求。

6 结论

本文以我国某桥梁工程实例为基础展开分析，借助Midas Civil 有限元分析软件计算了在给定地震作用下结构的抗震性能。研究结果表明，在地震作用下桥墩结构部分位置达到塑性阶段，在承受弯矩时首次屈服产生有限的局部变形，且伴随承载能力的下降，未出现破坏现象，结构整体基本完整。各桥墩的变形量也处于允许范围内，桥墩所受剪切强度小于容许值，满足基本承载要求，不会出现倒塌、破坏的情况，满足我国现行规范要求。