基于精确Zoeppritz方程和改进人工蜂群算法的AVO反演方法研究

罗红梅,王长江,智龙霄,颜世翠,张志敬

(1.中国石油化工股份有限公司胜利油田分公司勘探开发研究院,山东东营 257015;2.华北水利水电大学地球科学与工程学院,河南郑州 450046)

叠前弹性参数反演是利用叠前地震信息、测井资料及地质信息反演地下的相关储层参数、预测储层以及流体的一种方法。叠前AVO(Amplitude variation with offset)反演基于地震反射振幅随炮检距变化的规律,使用叠前共中心点道集数据求取反射界面上、下介质的物性参数信息,主要包括纵波速度、横波速度和密度等。相比于叠后反演方法,AVO反演具有良好的保真性和多信息性,并且理论较为成熟,可以更为精确地提取反映岩石含油气性以及岩性的属性参数,从而提高流体识别和储层预测的精度,在油气勘探中得到了广泛研究和应用[1-3]。

目前AVO反演的发展主要集中在以下两个方面。①基础理论方面,通过对反射系数方程进行改进以提高反演的精度和效果,其主要发展趋势有:从Zoeppritz方程线性近似表达式发展为精确Zoeppritz方程,从单相介质反演发展为双相介质、各向异性介质反演,从单一的PP波数据反演发展为PP波和PS波数据联合反演,以及从时间域反演发展为时间域和频率域数据联合反演,等等[4-8]。②反演算法方面,虽然AVO反演被广泛应用于油气勘探,但是仍然面临着反演效率低、反演精度不高等问题,探索有效的反演技术流程和高效的反演算法是促进AVO技术发展的动力。为了提高叠前AVO反演储层物性参数的可靠性,贝叶斯理论、智能优化算法、机器学习算法等被逐渐引入AVO反演,例如模拟退火、遗传算法、粒子群算法、蚁群算法等,这些智能优化算法具有不依赖或弱依赖于初始模型、不需要求解复杂的雅可比矩阵、算法实现较简单等优点,已经广泛应用于地球物理反演的研究中,实现了储层多参数岩相预测,取得了很好的效果[9-14]。

为了进一步提高反演的收敛精度,避免局部极小值问题,本文引入改进的人工蜂群算法。蜂群算法是近年来发展的智能优化算法,是集群智能思想的一个具体应用,该算法根据蜜蜂的行为而提出,主要分为基于繁殖行为与基于采蜜行为两大类。最常用的基于蜜蜂繁殖行为的蜂群算法是ABBASS[15]于2001年提出的蜜蜂交配优化算法(Honey bee mating optimization,简称HBMO),除此之外还有蜜蜂进化型遗传算法和蜂王算法等。最常用的基于蜜蜂采蜜行为的蜂群算法是KARABOGA[16]于2005年提出的人工蜂群算法(Artificial bee colony algorithm,简称ABC)。蜂群算法的主要特点是不需要了解问题的具体信息,只需要对问题进行优劣比较,通过各人工蜂个体的局部寻优行为,最终在群体中使全局最优值突现出来,有着较快的收敛速度。目前,蜜蜂的采蜜行为、学习行为、记忆和信息分享特性已成为群体智能的研究热点之一,应用前景十分广阔[17-20]。

目前常规的叠前AVO反演主要基于Zoeppritz方程线性近似表达式提取弹性参数,近似式虽然形式简明、使用方便,但是存在一定的局限性,例如密度的反演不稳定、要求反射界面两侧弹性参数变化不大、入射角较小等;如果使用常规的线性反演或者非线性反演方法,其反演精度有限,并且容易陷入局部极小,受各种噪声和采集过程中不确定因素的影响很大。针对以上问题,本文提出了基于精确Zoeppritz方程和改进人工蜂群算法的叠前AVO反演方法。首先基于精确的Zoeppritz方程,结合贝叶斯理论,推导反演的目标函数;然后将改进的人工蜂群算法引入AVO反演,实现对储层纵波速度、横波速度和密度的高精度反演;最后采用理论模型数据和实际地震资料进行测试,证明该方法的有效性和可行性。

1 方法原理及实现

1.1 基于精确Zoeppritz方程和贝叶斯理论的目标函数构建

针对常规的基于Zoeppritz方程线性近似表达式的AVO反演方法所存在的局限性问题,本文采用精确的Zoeppritz方程进行AVO反演,并结合贝叶斯理论构建反演目标函数。假设入射角为θ,采样点个数为n,使用AKI等[21]根据Zoeppritz方程推导的纵波反射系数的精确解(见附录A),n个采样点处的纵波反射系数方程可以分别表示为:

式中:RPPi(θ)(i=1,2,…,n)表示第i个采样点处入射角为θ时的纵波反射系数;vPi,vSi,ρi分别表示第i个采样点处上层介质的纵波速度、横波速度和密度;vP(i+1),vS(i+1),ρi+1分别表示第i个采样点处下层介质的纵波速度、横波速度和密度;f表示纵波反射系数关于纵波速度、横波速度和密度的非线性函数。可将(1)式整合为矩阵函数的形式:

r(θ)=f(m)

(2)

式中:r(θ)=[RPP1(θ),RPP2(θ),…,RPPn(θ)]T表示入射角为θ时的反射系数序列;m=[vP1,vP2,…,vP(n+1),vS1,vS2,…,vS(n+1),ρ1,ρ2,…,ρn+1]T为包含纵波速度、横波速度和密度的弹性参数序列;f为正演算子,表示反射系数r与弹性参数m之间的非线性关系。用w表示地震子波,通过地震子波与反射系数的褶积合成地震记录,将(2)式等号两侧同时与地震子波进行褶积,得到入射角为θ时地震记录与弹性参数之间的关系:

s(θ)=w*r(θ)=w*f(m)

(3)

其中,*为褶积符号,s表示地震记录。假设有m个入射角θ1,θ2,…,θm,对应的地震记录方程分别为:

s(θ1)=w(θ1)*f1(m)
s(θ2)=w(θ2)*f2(m)
⋮
s(θm)=w(θm)*fm(m)

(4)

其中,f1,f2,…,fm分别表示入射角为θ1,θ2,…,θm时反射系数与弹性参数之间的非线性函数。将不同入射角对应的地震记录方程联立起来,简写为:

s=g(m)

(5)

其中,

(6)

(7)

(5)式即为使用精确的Zoeppritz方程,通过褶积模型合成地震记录的正演方程。

贝叶斯理论在AVO反演中的应用非常广泛,可以用于求解病态问题,提高反演的稳定性。用d表示实际观测得到的地震角道集记录,m表示模型参数,根据贝叶斯理论可以推导得到模型参数m的后验概率分布(见附录B)。使模型参数的后验概率最大化,相当于使其指数项的负数最小,据此可以建立极小化的目标函数,即:

(8)

式中:mc表示纵波速度、横波速度和密度的相对变化,符合柯西分布;σn为数据噪声的标准差,此处的作用是控制柯西先验分布约束项的权重;Φi中包含有协方差矩阵,作用是将3个AVO参数之间的统计相关性引入反演以提供约束。

为了补偿低频信息,在目标函数中添加模型约束项,此时目标函数的最终表达式为:

(9)

1.2 改进人工蜂群算法的构建

针对(9)式目标函数的反演优化问题,我们构建了一种改进的人工蜂群优化算法。人工蜂群算法的基本流程如图1所示。首先进行初始化,随机产生初始群体,假设有N个初始解,其中N为采蜜蜂的数量,也等于蜜源数目。每个解Xi(i=1,2,3,…,N)是一个D维的向量,D为优化参数的个数。在初始化以后,以这些初始解为基础,采蜜蜂、观察蜂和侦察蜂开始进行循环搜索。

图1 人工蜂群算法的基本流程

蜂群算法通过上述流程进行搜索,算法中的每个蜜源代表优化问题中的一个可能解,蜜源的质量对应解的质量,用适应度值表示。人工蜂群算法的优点在于通过模拟蜂群的智能采蜜行为,蜜蜂根据各自的分工进行不同的采蜜活动,并实现蜜源信息的共享和交流,从而找到问题的最优解,算法具有结构简单、易于实现、无需梯度信息、参数较少等特点。但是标准的人工蜂群算法存在易于过早陷入局部最优点的问题,进化后期收敛速度慢,对过于复杂的问题可能搜索不到最优解,计算精度不高。

在人工蜂群算法中,已知当前记忆位置为Xi,通过(10)式所示的蜜源搜索方程产生新的候选位置Vi:

vi,j=xi,j+φi,j(xi,j-xk,j)

(10)

式中:xi,j为Xi中的元素;vi,j为Vi中的元素;k,j是随机选择的下标,满足k∈{1,2,…,N},j∈{1,2,…,D},k≠i;φi,j为[-1,1]之间的随机数。由(10)式可以看出,人工蜂群算法具有很强的邻域搜索能力,但因算法未有全局最优值参与计算,致使该算法因全局探测能力不足而陷入局部最优解。人工蜂群算法收敛速度较慢,究其原因就是(10)式所示的搜索公式决定了其精于探索、疏于开发的特性。为了增强算法的开发能力,借鉴粒子群算法,使用全局最优解引导的人工蜂群算法可以较好地增强算法的开发能力,其搜索公式为:

vi,j=xi,j+φi,j(xi,j-xk,j)+α(xG,j-xi,j)

(11)

其中,xG,j为XG中的元素,XG=[xG,1,xG,2,…,xG,D]为全局最优解,通过调节α的值可以很好地平衡算法的探索与开发能力,α取0～1.5的随机值时优化效果较好。

蜂群搜索(11)式中的全局项α(xG,j-xi,j),虽然可以平衡算法的探索与开发能力,但是会在一定程度上降低算法的全局寻优能力,为此,进一步借鉴遗传算法中的交叉运算来加强蜂群算法的开发能力,采用基于交叉运算的全局人工蜂群算法,将遗传算法与基本的人工蜂群算法相结合。遗传算法是一种借鉴生物界自然选择和进化机制发展起来的具有自适应性和自组织能力的搜索算法,包括选择、交叉和变异3种操作,被广泛应用于求解复杂的优化问题。常见的交叉操作包括指数交叉和二项交叉,本文采用二项交叉与人工蜂群算法相结合。对于二项交叉,首先对每一个分量都生成一个0～1均匀分布的随机值u,使用cr表示交叉系数,若u≤cr,则接受目标分量,否则保留当前个体的对应分量。如果采蜜蜂邻域搜索后与全局最优值进行交叉操作,具体表示为:

(12)

设想可以让采蜜蜂进行邻域搜索后与全局最优值进行交叉操作来提高人工蜂群算法的开发能力,但是单纯地与全局最优值二项交叉会限制算法的探索能力,为了增加算法的搜索能力,建立交叉操作的公式,即:

(13)

(13)式中,通过交叉系数cr来协调算法的探索能力和开发能力,cr越大时越有利于增强算法的开发能力,但是会降低探索能力;cr越小时越有利于增强算法的探索能力,但是会降低算法的开发能力。需要根据实际情况的不同合理调节交叉系数cr以实现高效、稳定的最佳寻优。β取-1～1的随机值,以避免过多降低算法的探索能力而出现提前收敛的情况。

1.3 改进人工蜂群算法与AVO反演的融合

人工蜂群算法是一个最大优化过程,通过适应度函数来体现,而AVO反演是一个最小优化问题,通过目标函数来体现。将AVO反演与蜂群算法相结合,关键在于得到适应度函数与目标函数之间的关系。本文建立的对应关系为:

(14)

式中:fiti为第i个蜜源的适应度值;φi为第i个蜜源对应的目标函数值,i=1,2,3,…,N。利用(14)式,即可根据目标函数计算得到相应的适应度值。

由此,建立基于改进人工蜂群优化算法的叠前AVO反演方法,其实现过程如图2所示。

图2 基于蜂群优化算法的叠前AVO反演技术流程

2 模型试算

根据测井资料建立一维模型,模型参数包括纵波速度(vP)、横波速度(vS)和密度(ρ)。基于精确的Zoeppritz方程,通过褶积模型合成地震记录,利用该合成地震记录进行基于改进人工蜂群算法的AVO反演测试,以证明算法的有效性和可靠性。

2.1 基于改进人工蜂群算法的AVO反演

取一段测井资料建立测试模型,设置相应的纵波速度、横波速度和密度等模型参数(图3)。根据(5)式,利用模型参数和主频30Hz的雷克子波,基于精确的Zoeppritz方程,正演得到合成地震记录(图4)。

图3 测试模型参数a 纵波速度; b 横波速度; c 密度

图4 人工合成的角道集地震记录

基于改进的人工蜂群算法,使用人工合成的角道集地震记录进行AVO反演测试,分别用蓝线、黑线和红线表示真实结果、低频模型和反演结果(图5)。对比可以发现,3个参数的反演结果与真实结果均非常相近。进一步地,计算反演结果的平均相对误差来评价反演效果,纵波速度、横波速度和密度的平均相对误差分别为1.43%,1.60%和0.55%,反演效果较好。

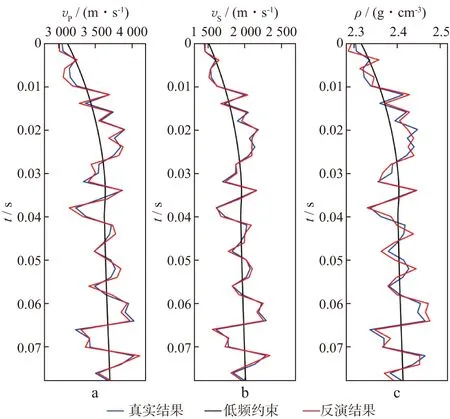
图5 基于改进人工蜂群算法的AVO反演结果a 纵波速度; b 横波速度; c 密度

2.2 参数优选

该反演中涉及到的参数主要有蜂群大小、蜜蜂最大搜索次数、蜜蜂搜索空间的上界和下界、模型约束项、柯西先验分布约束项等,本节分别测试这些参数对反演结果的影响。

蜂群大小参数与算法的寻优能力、收敛速度有关,如果取值过小,则算法陷入局优的可能性很大;如果取值过大,则算法的优化能力很好,但收敛速度慢;当蜂群大小增长至一定水平时,继续增大群体数目将不再有显著的作用。蜜蜂最大搜索次数的作用是,如果蜜蜂搜索次数超过该限定值仍然没有发现更高花蜜量的蜜源,则放弃该蜜源,转化为侦查蜂,在全局范围内随机产生一个新蜜源,该机制可以让算法较好地跳出不合适的搜索范围,避免陷入局部最优。

分别测试蜂群大小和蜜蜂最大搜索次数对算法收敛情况的影响,结果如图6所示。图6a中,蓝、黑、红、绿、青、紫6条线分别表示蜂群大小取50,100,150,200,250,300时的目标函数收敛情况,右上角线条后面的数据表示计算用时;图6b中,蓝、黑、红、绿、青、紫6条线分别表示蜜蜂最大搜索次数取5,10,15,20,25,30时的目标函数收敛情况,右上角线条后面的数据表示计算用时。由图6可以看出,蜂群大小取值越大,目标函数的收敛情况越好,计算用时越长;蜜蜂最大搜索次数参数取值大小对计算用时没有显著影响,在一定范围之内对目标函数的收敛具有一定的影响。因此,反演过程中需要根据研究目标的具体情况,通过参数优选选取合适的数值,保证计算效率最佳。

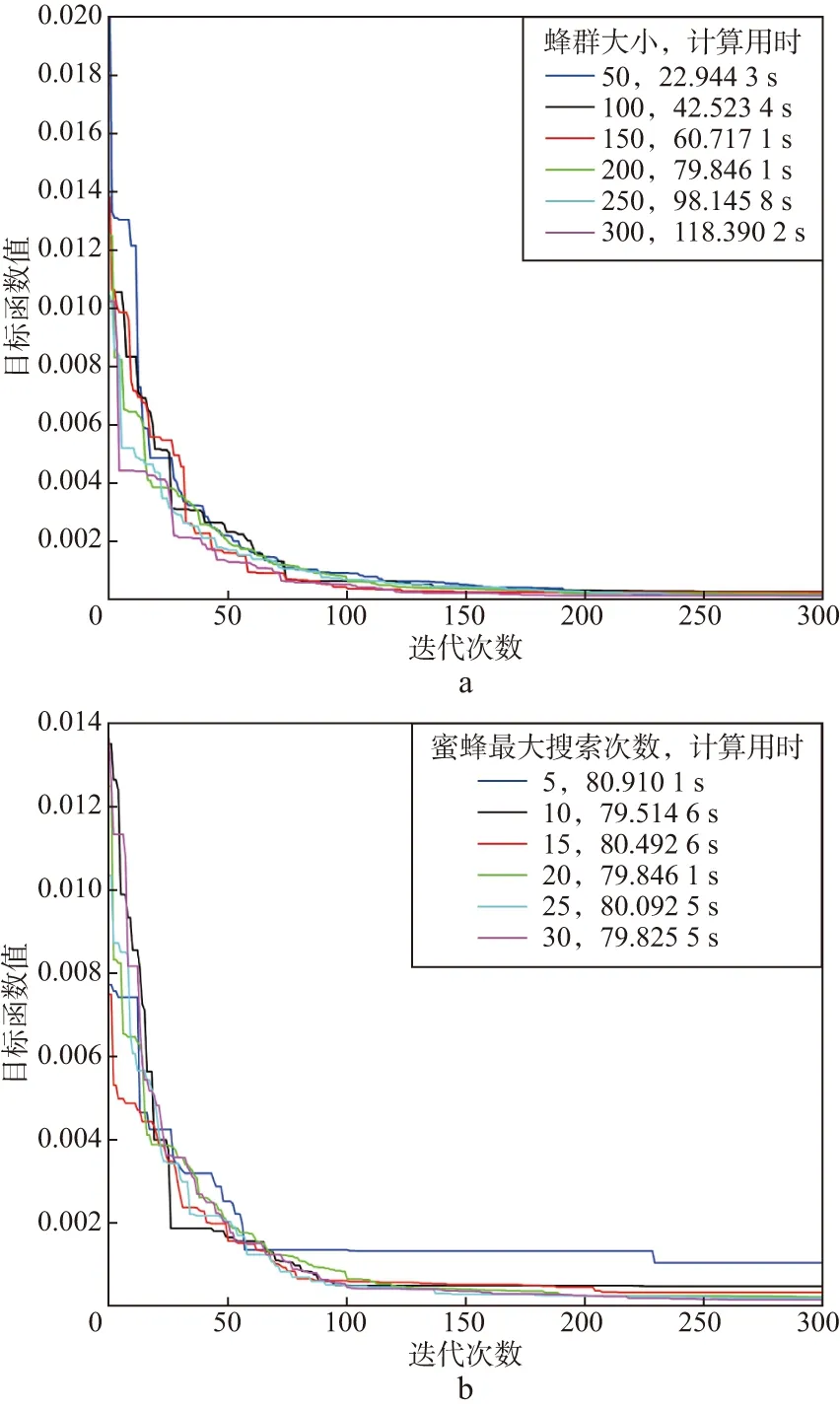
图6 蜂群大小(a)和蜜蜂最大搜索次数(b)对算法收敛情况的影响

蜜蜂搜索空间的上界和下界主要是对蜜蜂的搜索范围进行约束,在蜜源的位置更新之后,判断是否存在超出蜜蜂搜索空间范围的位置,如果存在则将该位置替换为搜索边界的位置。一般来说,蜜蜂搜索空间的范围越准确,反演的稳定性越好,结果越准确。而模型约束项的作用是在蜜蜂搜索空间上、下界的基础上,对反演结果进行进一步的约束,如果减小模型约束项的权重,可以看到,当模型约束项权重系数由1.0×10-14减小为1.0×10-16时,反演结果中3个参数与真实结果均会发生较大的偏离(图7)。进一步地,将反演结果合成得到的地震记录与原始地震记录进行对比,结果如图8所示,可见,二者之间的差异非常小。结果表明,减小模型约束项的权重后,虽然反演结果合成的地震记录与原始地震记录非常接近,但是反演结果与真实结果之间却具有较大的误差,说明模型约束项是反演过程中非常关键的一个参数。

图7 减小模型约束项权重时的AVO反演结果a 纵波速度; b 横波速度; c 密度

图8 反演结果合成的地震记录与原始地震记录的对比a 原始地震记录; b 反演结果合成的地震记录; c 两个地震记录之间的差异

另外,柯西先验分布约束项中,尺度矩阵包含了模型参数之间的相关信息,可以提高反演的稳定性;柯西分布还具有长尾巴特征,可以为反演提供稀疏约束,得到高分辨率的解。如果不使用柯西先验分布约束,将该项的权重系数设为0,反演结果如图9所示。对比可见,一方面无先验约束的反演结果与真实结果、有约束的反演结果之间差异较大;另一方面无先验约束的反演结果中细节信息大大减少,反演结果的分辨率明显降低(图9)。

图9 无柯西先验分布约束时的AVO反演结果a 纵波速度; b 横波速度; c 密度

通过分析本反演方法中涉及的5种参数对反演结果的影响,进一步明确了参数优选对反演结果质量的重要性。

2.3 噪声影响

进一步地,在地震记录中分别添加信噪比(SNR)为10,5,3,1的随机噪声,利用本文方法对这4种数据分别进行反演,以测试噪声对反演结果的影响(图10),并分析不同强度噪声影响下人工蜂群算法的AVO反演误差(图11)。由图10和图11可以看出,随着噪声增大,反演结果与真实结果差异变大,反演误差也在逐渐增大,但是反演结果仍然较为稳定,误差均在可接受的范围之内。因此,在噪声的干扰下,改进的人工蜂群算法仍然可以取得较为稳定的反演结果,说明该方法具有较好的抗噪性。

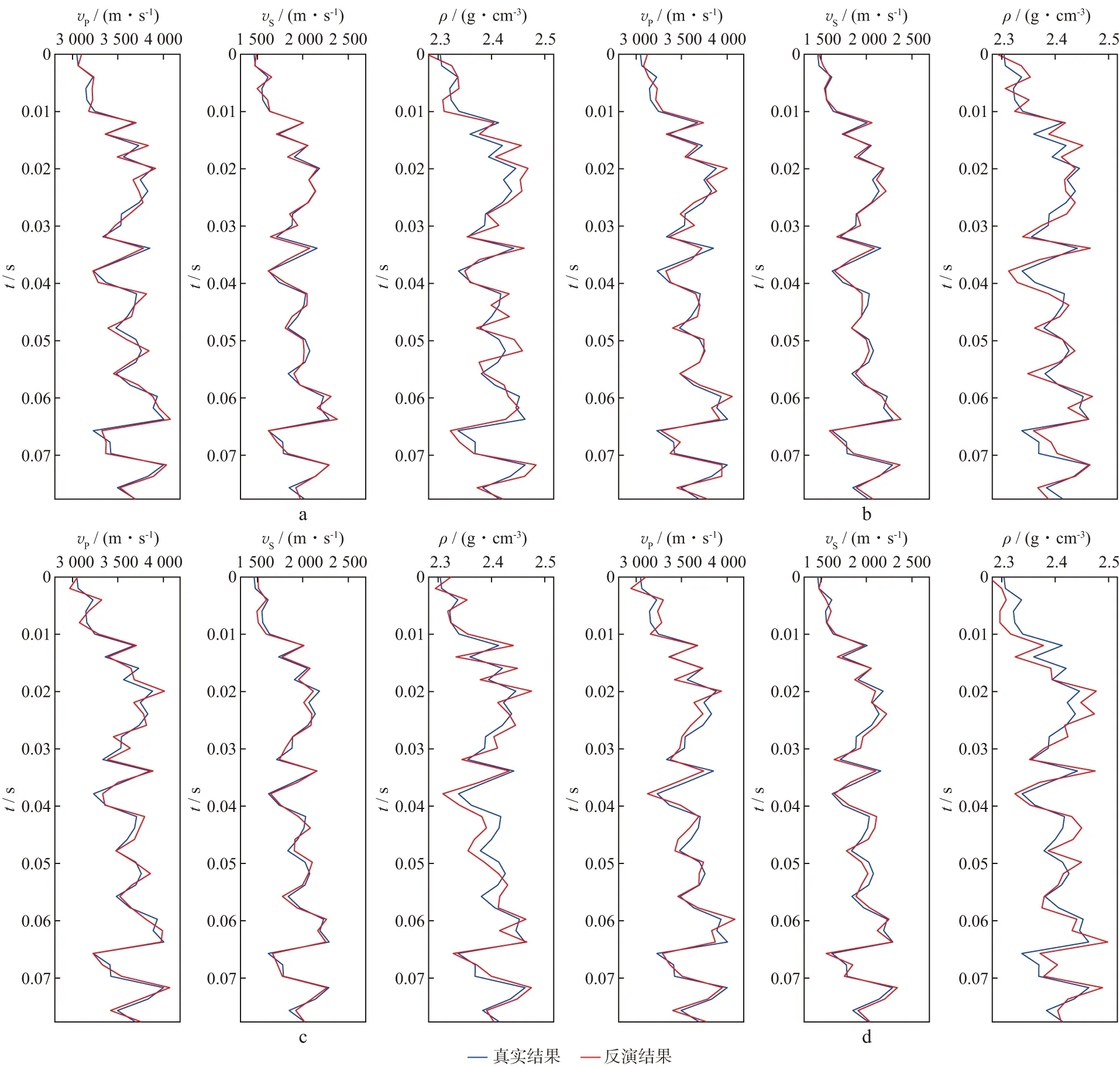
图10 不同噪声影响下基于改进人工蜂群算法的AVO反演结果a SNR=10; b SNR=5; c SNR=3; d SNR=1

图11 不同强度噪声影响下的反演误差变化

2.4 方法对比

分别使用常规方法、改进前的人工蜂群算法、改进后的人工蜂群算法进行叠前AVO反演,结果如图12 所示。表1对比了常规方法、改进前人工蜂群算法、改进后人工蜂群算法的叠前AVO反演误差。由图12和表1可以看出,相比于常规方法,人工蜂群算法的反演效果更好;改进后和改进前人工蜂群算法的反演结果较为相近,但改进后人工蜂群算法的反演效果更好,误差更小。

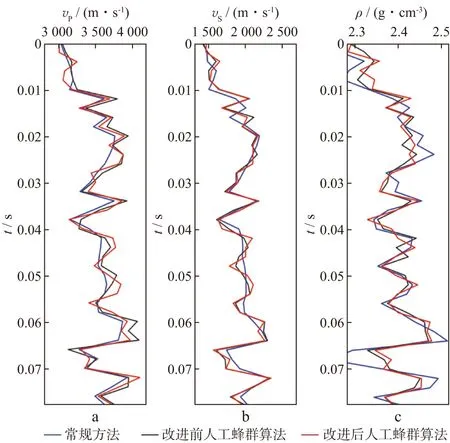
图12 常规方法、改进前人工蜂群算法、改进后人工蜂群算法的叠前AVO反演结果a 纵波速度; b 横波速度; c 密度

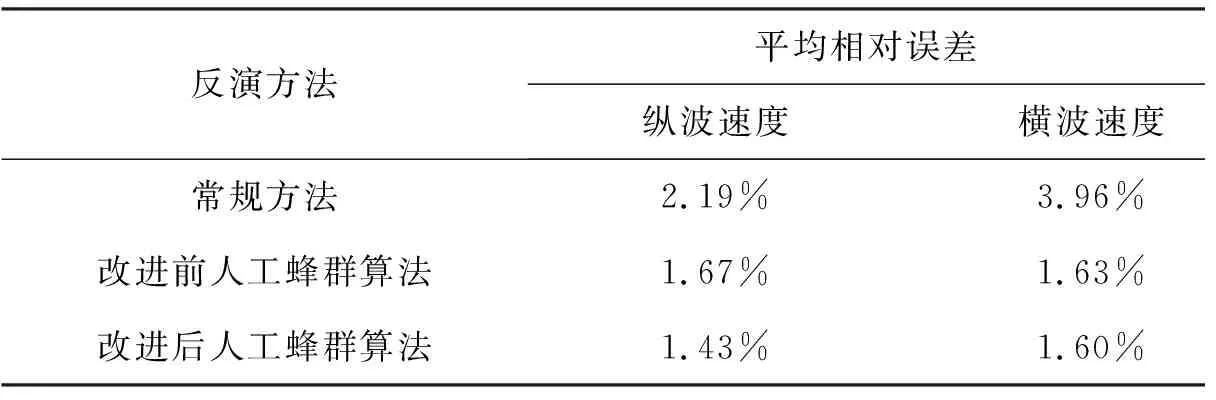
表1 常规方法、改进前人工蜂群算法、改进后人工蜂群算法的叠前AVO反演误差

3 应用实例

研究区位于济阳坳陷东营凹陷中央隆起带东部的东辛—广利周缘地区,其沙四上亚段油藏类型以构造、岩性油藏为主,上部为扇三角洲构造油藏,下部为滩坝砂岩性油藏,储层纵、横向发育特征变化较快,利用常规反演等方法预测有效储层时精度较低,严重影响了研究区勘探部署。

研究区沙四上亚段既有北部来自青坨子凸起的物源,又有南部物源,导致沉积和油气富集规律都比较复杂。从测井特征上看,砂岩表现为低伽马、低自然电位、高阻抗的特征,大套泥岩表现为高伽马、高自然电位、低阻抗的特征。但从地震上看,砂岩呈现为中强振幅的反射特征,大套泥岩表现为中弱振幅的反射特征。由于沙四上亚段多套砂体纵向上相互叠置,横向上厚薄变化大,因此实钻井油水关系复杂。纯上5砂组高部位为含油水层,低部位为油层,地震上表现为连续、中强振幅反射,现有的地震反演等技术手段难以实现砂体边界的准确识别。

针对研究区储层分布特点及岩电震特征,利用本文方法反演储层的纵波速度、横波速度和密度参数,以刻画砂体空间展布特征。经过道集优化处理、初始模型建立、地震子波提取、人工蜂群算法相关参数优选,对优化后的角道集数据体进行基于改进人工蜂群算法的AVO反演。

首先使用过井的地震数据进行反演参数的优选,通过与测井资料进行对比,计算平均相对误差以评价反演结果的优劣。本文方法中,影响反演效果的因素主要分为3类:①与数据处理相关的影响因素,如信噪比增强处理、地震子波选取、角道集提取等;②AVO反演目标函数中的相关参数,例如柯西先验约束项权重、低频模型约束项权重等;③人工蜂群算法中的相关参数,例如蜂群大小、蜜蜂最大搜索次数、蜜蜂搜索空间的上界和下界、迭代终止条件等。这些参数均会对反演结果产生一定的影响,反演前需要优选,选取适用于该工区地质特征的反演参数。

分析过典型井的纵波速度反演剖面(图13a,图13b)可以看出,其综合揭示的砂体产状及纵向边界与实钻井信息吻合较好,砂体接触关系符合地质发育规律。lai17井相对于lai51井和lai38井在沙四上亚段储层发育略差,砂体纵向厚度略薄但测井解释为油层,lai51井储层发育且砂体厚度较大,构造上相对于lai17井位于构造高部位却为含油水层,反演剖面上,从低部位到高部位砂体互不连通,其刻画出的砂体分布特征可以较好地解释该现象(图13)。同样,构造部位稍低的lai38井亦钻遇砂体厚度相对较薄的油层,反演结果也表明lai38井与lai51井之间的砂体接触关系为不连通(图13a)。在前人方法的反演剖面上,虽然纵向视分辨率略高于本文方法的结果,但可靠性相对较差,如lai17井与lai51井之间、以及lai38井与lai51井之间的目标砂体均表现出连通的特征,这与实际地质规律不符。因此,相对于前人方法结果(图13b)而言,本文方法速度反演结果对砂体的连通性刻画更加合理,对目的层砂体展布特征更具预测性。

图13 过lai17-lai51-lai38井的反演结果分析a 本文方法; b 前人方法; c 录井图

具体地,分析lai38井的井旁道反演结果(图14)可以看出,反演结果与实测曲线变化特征基本一致,局部细节上的差异是由于地震反演的分辨率所致。与常规反演方法得到的结果相比,本文方法的反演结果与实际井的钻探结果更加吻合。

图14 lai38井的井旁道反演结果a 纵波速度; b 横波速度; c 密度

进一步地,分析研究区内多口井的井旁道反演结果,计算反演结果与测井曲线之间的平均相对误差和相关系数,结果如表2所示,可以看出:纵波速度平均相对误差均在5%以内,横波速度平均相对误差略高一些,多在4%～8%,密度误差较小,均小于2%;反演结果与测井曲线之间的相关性较好,相关系数大都在60%以上。对比本文方法和常规方法的平均相对误差与相关系数可知,由本文方法得到的三参数反演结果相对误差大大减小,与实际测井曲线的相关系数明显高于常规方法的结果,说明本文方法的反演结果整体上优于常规方法的反演结果,具有更好的可预测性。

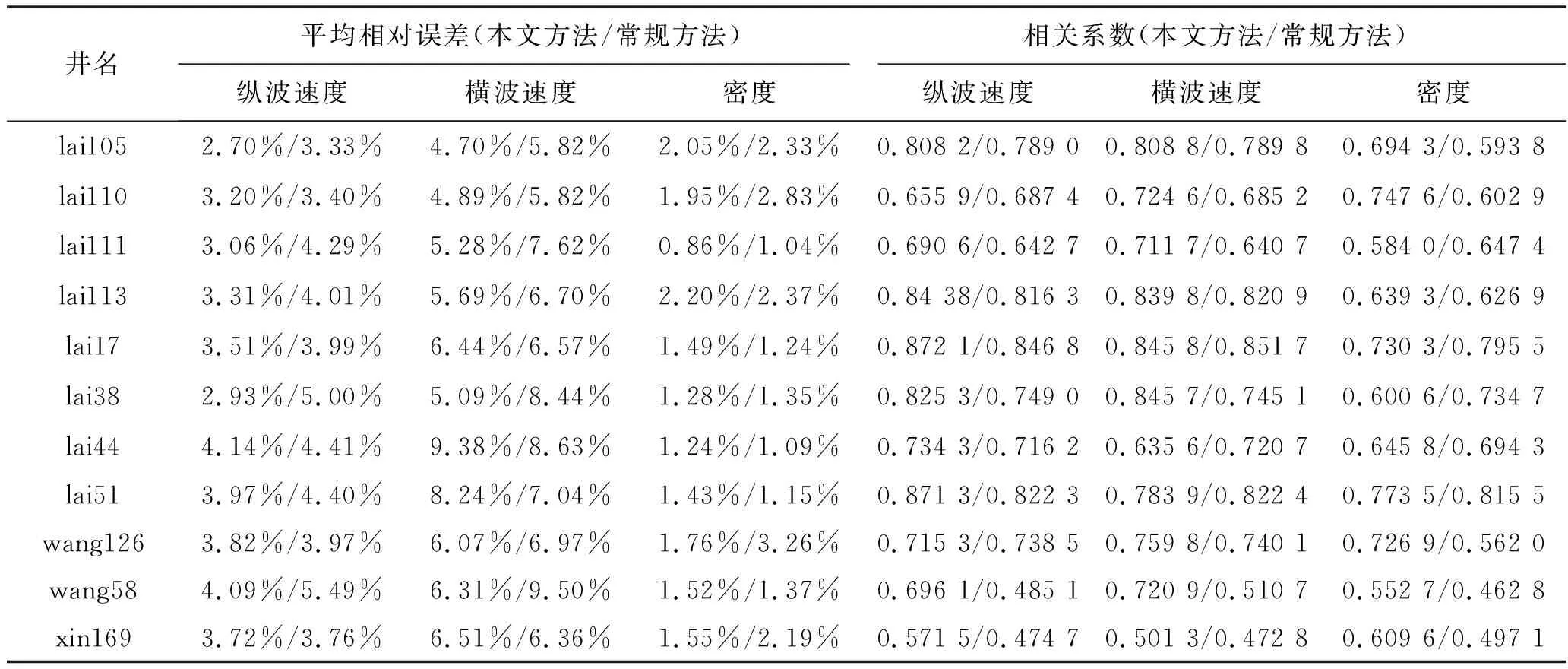
表2 井点反演结果与测井曲线之间的平均相对误差和相关系数

由于研究区储层分布特征与纵横波速度和密度等弹性参数具有较好的对应关系,为了更好地分析沙四上亚段储层的平面展布规律,提取反演结果的平面特征可以发现,纵波速度、横波速度、密度3个参数表现出来的规律基本一致,以提取的最大纵波速度属性为例,其较好地刻画了西南部wang58井区储量探明范围的边界,同时也清晰地表征了东部lai51-lai38近东西向、lai113井区北西向展布的多个有利储层发育区的形态(图15a)。同时,与前人方法结果(图15b)进行对比,并对实钻井钻遇情况进行统计分析,可以看出,本文方法对储层平面展布特征的刻画更加符合研究区地质规律,与实钻井更加吻合,储层预测吻合率达到80%以上。以此结果为依据可以预测laix117井西南部及lai24井东部均发育了有利储层,反演结果为井位目标的选取提供了有力依据。

图15 研究区沙四上亚段纵波速度反演结果对比a 本文方法; b 前人方法

4 结论

针对常规的叠前AVO反演方法在基础理论与反演算法方面的不足,本文提出了基于精确Zoeppritz方程和改进人工蜂群算法的AVO反演方法。使用精确的Zoeppritz方程和贝叶斯理论推导出反演的目标函数,避免了常规的采用近似公式叠前反演在大入射角时失真问题,同时增加低频约束信息,进一步提高反演的稳定性和准确性;将遗传算法和粒子群算法的思想引入到蜂群算法中,并将改进的人工蜂群算法与叠前AVO反演相融合,克服了常规的基于Zoeppritz方程线性近似表达式的反演方法所存在的局限性问题。通过理论模型数据分析蜂群大小、蜜蜂最大搜索次数、蜜蜂搜索空间的上界和下界、模型约束项、柯西先验分布约束项等参数对反演结果影响的测试表明,本文方法的稳定性和准确性优于常规方法。实际研究区地震数据的处理、反演与解释结果表明,本文方法较好地反演出砂体的纵向叠置与横向连通关系,与实钻井吻合率较常规反演方法大幅提高,平面预测结果更加符合研究区的地质变化规律。采用本文方法可以进一步通过弹性参数反演准确提取储层的物性参数,从而精确预测有效储层分布,同时将改进的人工蜂群优化算法与叠后反演相结合,提升反演的可靠性,可以进一步拓宽其应用空间。