基于动态平面波的三维多尺度全波形反演方法

国运东,孟凡冰,秦广胜,李传强,李庆洋

(中国石油化工股份有限公司中原油田分公司物探研究院,河南濮阳 457001)

全波形反演方法(FWI)综合利用地震数据的走时、相位、振幅等全波场信息,通过地震数据与模拟数据的差值建立目标泛函,不断更新地下参数模型,使得模拟地震数据越来接近观测数据,从而达到建立不同参数场的目的,FWI是一种高精度、高分辨率的物性参数建模方法。与常规的射线层析以及偏移速度分析(MVA)速度建模方法相比,FWI具有更高的分辨率以及速度建模精度,但是其在应用中仍然存在许多问题,针对FWI不同问题的解决方法也相继被提出[1-5]。

20世纪80年代,TARANTOLA[6]首先建立了全波形反演的理论框架,但是在缺少低频和背景场不准确的情况下,容易引起周波跳跃现象。BUNKS等[7]提出了分频多尺度反演方法与网格多尺度反演方法,指出在大网格、低频尺度下反演的背景速度模型,可以有效解决全波形反演的周波跳跃问题;SIRGUE等[8]给出了频域多尺度FWI的频率选取策略[9];BOONYASIRIWAT等[10]构建了地震数据的维纳滤波器,实现了时域FWI的多尺度方法[11]。除利用地震数据中的低频组分反演背景速度模型外,MORA[12]和PRATT等[13]通过采用大偏移距以及透射波数据构建背景速度模型,避免了全波形反演过程中的周波跳跃问题[14]。SHIPP等[15]通过对地震数据进行分偏移距的反演,指出地震数据在大偏移距时,由于传播时间较长以及波形复杂性增加会加剧全波形反演的非线性。BAETEN等[16]和PLESSIX等[17]通过实际资料数据中的低频、大偏移距组分反演试算,证实了低频、大偏移距组分在实际地震数据反演中的重要性。但在实际地震数据采集中,想要获取质量非常高的低频、大偏移距数据信息比较困难,因此许多学者发展了不同的低频信息缺失情况下的背景速度模型构建方法。BOZDAG等[18]利用由Hilbert变换得到的瞬时相位与瞬时振幅信息构建新的波形反演目标泛函,降低了全波形反演的非线性;随后CHI等[19]提出基于地震包络的目标泛函,即利用波形的包络残差代替波形残差,并推导相应的梯度公式;WU等[20-21]通过对地震信号包络的研究,揭示了地震信号的调制-解调机制,指出地震信号中反映地下大尺度特征的长波长分量是通过非线性的方式与短波长分量的信号调制在一起的,应用包络反演可以构建这些低频分量,从而降低全波形反演的非线性。

另一方面,波数连续性对于全波形反演非常重要[22],从理论上讲,初始模型提供的低波数组分需要确保模型扰动能够反演在准确位置,否则会发生周期跳跃[23]。对于特定的初始模型,FWI的梯度必须保证波数域中覆盖范围的连续性。从模型的角度来看,可以通过梯度来直接访问特定波数分量[24],反射波全波形反演(RFWI)方法包含两步工作流程,其中反复交替更新背景速度和高波数模型,从而能够为FWI和偏移成像恢复准确的背景模型[23,25-27]。可通过对反射波进行成像方法,适当提取反射波场所携带的长波长信息,该成像可以计算对应于高散射角的反射层位到地面的透射波路径[28]。RFWI需要巨大的计算资源,包含FWI与最小二乘逆时偏移(LSRTM),一些学者使用其它方法来分离波场,如使用频域局部散射角滤波器从平滑背景模型中恢复长波数速度扰动[29-30],或者使用易于实现且有效的角度相关滤波技术,实现在平面波域中分离低波数成分,用于反演背景速度模型[31]。GUO等[32]将平面波反演方法应用于全波形反演的背景速度模型反演,为后续反演提供准确的背景速度模型。此外,计算效率也是限制FWI应用的关键因素之一,平面波编码的反演方法是提高计算效率的有效方法之一,其计算量不再与炮数量呈线性关系,而与射线参数的数量直接相关,通过正确选择射线参数,可以合理地抑制串扰噪声,由于射线参数的数量远小于炮的数量,因此大大地提高了计算效率[33-35]。

在实际野外采集数据中缺失有效的低频信号,因此低频数据重构反演或不依赖低频的低波数反演方法(例如反射波反演、包络反演)成为近年来反演的研究热点,但是反射波反演也存在计算量大的问题,快速有效地利用低波数成分进行初始速度模型反演具有重要意义。本文设计了一种适用于三维的动态锥面波编码的三维背景速度模型构建方法,在较差的初始模型和不含低频数据情况下,通过从低到高的序列中恢复波数分量,并且采用动态参考点平面波策略仅需要少量的平面波,达到高效构建背景速度模型的目的。

1 方法原理

1.1 基本原理

基于L2范数的全波形反演方法的目标函数[6]表示为:

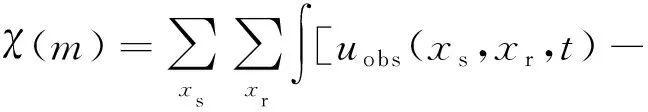
(1)

式中:uobs和ucal分别表示在t时刻的实际观测地震记录与正演模拟记录;震源点为xs;接收点为xr;m为速度参数模型。在波形反演过程中,需要多次迭代进行参数更新,因此计算量巨大,采用平面波编码反演是一种提高效率的方法。

在三维速度模型反演中,平面波需要2个射线参数px与py,然后通过时间延迟叠加获得平面波[33,35]:

Δtjk(p)=px(xsj-x0)+py(ysk-y0)

(2)

式中:(xsj,ysk)表示沿x测线第j炮与沿y测线第k炮的炮点位置;(x0,y0)表示合成平面波在地表的原始参考位置;x0与y0分别表示三维空间上的x轴(主侧线方向)位置与y轴(联络侧线方向)位置。应用平面波编码,通过改变射线参数p的动态平面波编码的全波形反演目标函数可定义为[33]:

(3)

本文提出的动态平面波编码由射线参数p控制波场的角度,波形反演的散射角信息常常与射线参数p相关,而在三维地震数据的波形反演中,地震波数的高低与散射角的大小密切相关,散射角的大小与射线参数的绝对值大小密切相关,常规平面波FWI含有两个方向的射线参数,因此很难控制与特定散射角大小的射线参数,为了在相同的射线参数p下(控制某一散射角)得到多个梯度,本文选取合适的射线参数和参考点构造特殊的平面波,即锥面波,并用锥面波对三维地震炮记录编码,得到锥面波超级炮记录,其中锥面波的生成函数为:

Δt[(xk,yk):p,(x0,y0)]=

(4)

式中:Δt表示时间延迟量;p为射线参数,其值越大表示锥面波的传播方向与地面夹角越大,与传统的平面波编码相比,其不再分两个方向,并且与地震波场的入射角相关;第k炮位置为需要编码的炮点位置,原始参考位置(x0,y0)为每次迭代随机选取的位置。

合成的锥面波超级炮记录可以表示为:

(5)

利用(5)式中的锥面波函数对震源子波编码,进行三维有限差分正演得到锥面波炮记录,锥面波对震源子波编码具体如下:

(6)

三维锥面波速度模型反演的目标函数表示为:

(7)

根据数据残差利用最速下降法或者共轭梯度法确定梯度,由于本文采用动态编码的方式,两次反演迭代之间的梯度场相差较大,因此采用最速下降法进行梯度更新。使用伴随状态方法[36],目标函数相对于模型参数的梯度可以通过以下方法获得:

(8)

1.2 反演流程

基于动态锥面波编码的三维背景速度模型构建方法的流程如图1所示。相比于传统的全波形反演,本文方法每次反演都需要选取不同的射线参数,在同一射线参数下,利用不同参考点,对炮记录和震源进行相同的动态锥面波编码,满足对这一射线参数的反演精度,再逐步减小射线参数,达到背景速度模型的反演目标,利用得到的背景速度模型进行常规全波形反演得到最终的速度模型。

图1 动态锥面波编码的全波形反演流程

2 模型测试

2.1 简单模型测试

简单模型如图2a所示。模型主要有3层介质,其中第二层中心部分存在一个洼陷,其速度大小与第一层相同,模型尺寸(x,y和z方向)为1500m×1000m×1300m,网格间距为10m,模型速度范围为3000～4000m/s。

计算参数:采用主频15Hz的雷克子波,采样时间长度为1.2s,采样间隔0.5ms,采用时间2阶、空间8阶的有限差分交错网格进行正演模拟,施加完全匹配吸收(PML)边界条件。观测系统:共有176炮(16×11),炮间隔10m,第一炮位置为(10m,0,0),地表全接收。采用线性梯度模型(图2b)作为反演的初始模型,反演过程中假定震源子波已知。

图3为不同三维地震炮记录以及数据残差。利用GPU进行3D正演模拟,使用10Hz主频的雷克子波作为目标子波,进行维纳滤波后的单炮记录如图3a 所示,炮点位于图2a的(500m,500m,10m)处,图上能清晰识别直达波与反射波等有效信息;图3b 为基于公式(6)合成的震源进行正演模拟的炮记录;图3c为根据公式(5)合成的锥面波超级炮记录,可以发现,由于不同单炮在时间和空间上的重叠,模拟波场较为复杂,表层能观测到能量较强的直达波场;图3d为基于公式(5)合成的锥面波超级炮记录与基于公式(6)合成的震源进行正演模拟的炮记录的残差,可以看出,直达波能量削弱,模拟波场更为复杂。将两种超级炮记录分别作为输入,为后续全波形反演提供基础数据。

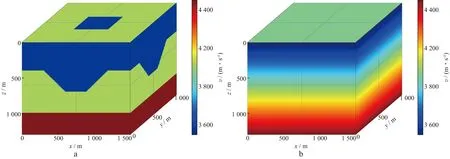
图2 反演采用的速度模型(洼陷模型)a 真实模型; b 梯度场的初始模型

图3 不同三维地震炮记录a 单炮记录; b 利用合成震源正演模拟的炮记录; c 根据公式(5)合成的锥面波超级炮记录; d 观测数据与模拟数据的残差

为了测试本文方法的有效性,本节采用维纳滤波多尺度的FWI方法进行对比,由于三维的计算量巨大,采用随机极性编码的方法将所有合成一个超级炮记录进行反演,不同频率子波维纳滤波后,炮记录的频率发生对应变化,滤波后的地震记录与对应主频子波产生的正演波场进行匹配达到频率多尺度反演的目的,当然极性编码也存在串扰噪声的影响,但是本节主要测试背景场的构建能力,因此暂不考虑串扰的影响,并且将极性编码的多震源多尺度FWI记为MFWI(Multi-source encoding multi-scale FWI)方法。

常规多震源编码FWI经过40次迭代后反演的速度模型如图4所示(截面:x=750m,y=750m,z=600m)。由于采用的是梯度场作为输入的初始速度模型,与真实速度模型存在较大的差异,且地震数据的主频比较高,波形反演过程中陷入局部极小值,使得洼陷构造的区域反演不清晰,无法有效地更新速度模型,洼陷结构很难恢复,只能看到洼陷的大体形态。由于上层反演不准确,洼陷下面层位的反演也不准确,变得弯曲。

图4 常规多震源编码FWI三维洼陷模型反演结果(10～15Hz)

然后利用锥面波多尺度全波形反演方法(CFWI)进行测试,结果如图5所示。测试中,平面波入射方向与z方向的夹角的正弦值从0.8减少到0.4,当数据误差收敛到一定数值,变化较小时,对同一射线参数p停止反演。测试中仅合成了1个锥面波,并且参考震源点随机地分布在表面上,每次迭代都改变。使用锥面波FWI(CFWI)进行反演结果如图5b所示,与利用MFWI反演(主频5～10Hz)结果(图5a)对比,可以观察到:①通过本文CFWI方法反演的背景速度模型与含有低频反演结果相似。②反演的洼陷构造的区域大体形态比较准确,并且洼陷构造下面的水平地层归位也相对准确。本文对单次梯度场的反演时间也进行了对比。采用相同的配置,CFWI方法需要8.6min,MFWI方法需要8.5min,传统的单炮叠加方法需要1393.2min,CFWI方法与MFWI方法的计算效率基本相近。由于本文采用了动态编码的CFWI,仅需要合成一个超级炮记录,就能达到反演背景速度模型的目的,因此大大提高了计算效率。

图5 三维洼陷模型采用不同多震源编码多尺度FWI的反演结果a 常规多震源编码多尺度FWI(MFWI)(主频5～10Hz); b 基于锥面波的CFWI(主频10Hz)

利用CFWI反演的背景速度模型为后续的MFWI提供了较为准确的背景速度模型。这样,使用相同子波的常规MFWI通过增加高波数分量进一步提高速度模型的反演精度(图6a),基本可以达到全频带多尺度的MFWI的反演效果(图6b)。

图6 不同背景场反演的三维洼陷模型结果a CFWI+MFWI; b 常规全频带多尺度FWI(MFWI)(主频5～15Hz)

2.2 复杂模型测试

3D逆冲模型(Overthrust模型)如图7a所示,由于模型过大,本文抽稀了一部分进行3D多震源多尺度FWI(MFWI)测试。测试中,深度方向采样点为100,Inline方向(x方向)采样点为201,Crossline方向(y方向)采样点为101,采样间隔为10m,模型速度范围为2428～6000m/s。该模型存在一个Inline方向的大型逆掩断层构造以及一系列的断块,纵向界面上发育有多条河道,整个模型的地质构造比较复杂。

计算参数:以主频15Hz雷克子波作为震源子波,地震记录的时长为1.2s,采样间隔0.5ms,采用时间2阶、空间8阶的有限差分交错网格进行正演模拟,施加PML边界条件。观测系统:共有231炮(21×11),炮间隔10m,第一炮位置为(10m,0,0),地表全接收,共20301个检波点,检波点间隔为10m。采用线性梯度模型作为反演的初始模型(图7b),反演过程中给定震源子波。

图7 三维Overthrust速度模型(a)和梯度场的初始速度模型(b)

本文以含有低频的MFWI结果作为标准进行对比。反演结果如图8所示。图8b中左侧部分断层以及河道等复杂构造,复杂区域的背景场反演比较准确,河道也刻画得比较清楚,验证了本文CFWI反演策略的有效性。应用不同的背景速度模型进行多尺度FWI反演,结果如图9所示。常规MFWI经过40次迭代后反演的速度模型如图9a所示。由于梯度场的初始模型与真实模型差异较大,并且数据的主频比较高,因此反演陷入局部极小值。河道的结构很难恢复,这时逆掩断层区域会出现强假象,深部的层位也位于不正确的位置,并且断层被强烈的低噪声污染。与初始模型的反演结果相比(图9a),应用CFWI+MFWI获得的最终速度模型比较准确(图9c),图上包括了断层和河道在内的大部分主要特征。主要断层和河道结构得到更好的反演,反射层位已经接近真实位置,动态编码压制串扰噪声效果较好,几乎与全频带多尺度MFWI结果相近(图9b)。相对传统三维单炮叠加的FWI方法,利用动态CFWI+MFWI,需要合成的超级炮数量大大减少,显著提高了计算效率。

图8 三维逆冲模型背景场反演结果a 常规多震源编码多尺度FWI(MFWI)(5～10Hz); b 基于锥面波的CFWI(主频:10Hz)

图9 三维逆冲模型最终反演结果a MFWI的反演结果(10～15Hz); b MFWI的反演结果(5～15Hz); c CFWI+MFWI的反演结果

3 结论及讨论

本文针对波形反演中地震数据缺少低频的情况下背景速度模型反演较为困难的问题,从低波数的反演角度出发,应用新的平面波合成方法,发展了一种基于平面波的有效低波数背景速度模型构建方法,通过模型试算和对比分析,得到如下几点认识。

1) 动态平面波多尺度全波形反演方法可以对单个射线参数合成更多的平面波,从而反演得到背景速度模型。在每次迭代选用少量不同的平面波也可以反演出较好的背景速度场,大大减小了计算量。

2) 将动态平面波方法与传统的FWI相结合,可以实现从低波数到高波数的速度模型反演,即使在缺少低频的情况下,也可以实现较高精度的速度模型反演,具有较好的收敛性和稳定性。

3) 针对三维观测系统,本文提出的锥面波编码多震源多尺度全波形反演方法(CFWI+MFWI),通过控制入射角的方式可以完成三维背景速度模型的构建。由于锥面波超级炮的个数远小于原始的普通炮集个数,因此该方法大大降低了计算量。

虽然本文提出的一种利用平面波的直接反演方法,通过直接利用低波数反演背景速度模型,避免了直接进行波数分离的过程,并且相对于反射波波形反演,避免了最小二乘的反演过程,但还存在观测系统的要求严格问题。此外在背景场准确情况下,多尺度反演策略在后期准确速度模型反演仍具有重要的意义,而且多震源方法存在固有的串扰噪声对中高波数反演的影响也比较明显,这也是后续要研究的主要方向。