淹没效应对不同类型琴键堰泄流特性的影响

李珊珊，李国栋※，姜 铎,2，沈桂莹

（1.西安理工大学省部共建西北旱区生态水利国家重点实验室，西安 710048； 2.榆林市淤地坝建设中心，榆林 719000）

0 引 言

堰通常用于人工运河、天然河道和水库中的流量测量、流量分流及流量控制等。在渠道或河流中应用堰作为挡水或控制建筑物时，由于绝大多数河流或渠道具有坡度缓、水流局部收缩或河道沿程尤其是下游植被多的特点，当下游水位超过堰顶高程时，就会产生淹没现象，进而影响堰的水头—流量关系。

相对于传统的直线堰（如薄壁堰、实用堰、宽顶堰等），琴键堰（Piano Key Weir，PKW）是一种新型的折线型迷宫堰，由于其堰轴线沿纵向被拉长，除了正向堰，还具有多个沿水流方向的侧堰，在堰上水头相同的情况下，琴键堰的泄流能力能高出4～5倍，因此被认为是大坝泄洪能力不足的非常有效且经济性很高的解决方案。且由于琴键堰倒悬的设计大幅减少了基础底座的占地面积，使其可以直接安装在现有重力坝的坝顶，极大拓宽了其应用范围。因此，现有的大多数研究都是基于琴键堰作为坝顶溢洪道应用时，在自由出流条件下的水力性能、几何参数及泄流能力。但除了作为大坝溢洪道的溢流堰以外，琴键堰也同样可以在人工或天然河道中作溢流坝及拦河坝使用，如2010年越南的Van Phong琴键堰拦河坝，是迄今为止世界上最长的琴键堰工程。Anderson等的研究也表明，对于底座基础在宽度或长度上受到限制的渠道或河流，琴键堰由于其紧凑的几何结构，可能会产生比迷宫堰更高的总泄流量。在自由流条件下，琴键堰的水头流量关系主要由其几何形状和来流条件决定，而当其应用在坡度较缓或下游植被茂密的河道中，则必须考虑由下游尾水抬升而引起的淹没的影响及其在淹没出流情况下的泄流效率。

研究堰淹没出流情形的初始方法是描述淹没对薄壁堰的影响时的流量折减系数法，这种方法也可以用来描述迷宫堰，甚至琴键堰的淹没水力特性。而Tullis等在研究迷宫堰和线性堰淹没特性时，提出了一种新的迷宫堰淹没特性关系式，称为无量纲水头法，研究表明该方法在描述迷宫堰淹没情形下水力性能方面比传统的Villemonte关系式更为准确。近年来，很多学者也尝试用这种方法研究琴键堰在渠道应用中的淹没情形。Belaabed等用以上两种方法对出口设置台阶式填充物的琴键堰在淹没出流下的水力特性进行了简单计算，确定了出口设置台阶的A型琴键堰的临界淹没度；Dabling等将上述新方法应用于比较标准体型和设有圆形堰鼻的优化体型琴键堰对淹没的敏感性，其研究表明优化的琴键堰体型对淹没效应的敏感性更高；Cicero等也用这种新的描述方法，对法国电力公司（Electricité de France，EDF）国家水力学和环境实验室（the National Laboratory of Hydraulic and Environment，LNHE）中A型、B型和C型三种典型琴键堰在淹没条件下的泄流效率进行了比较。总的来说，由于在琴键堰作为坝顶溢洪道应用时，淹没通常并不是主要考虑因素，目前关于其淹没效应的研究还非常少，描述其淹没效应的理论方法也很不完善，因此有必要将琴键堰的不同类型考虑在内，开展琴键堰的淹没特性研究，以系统比较各类琴键堰对淹没的敏感性及淹没条件下的泄流效率。

本文采用物理模型试验，对四种琴键堰在淹没出流条件下的过流情形进行测试，得到各琴键堰在淹没条件下的流态随下游水位的变化过程及上下游堰上水头之间的响应关系；分别采用流量折减系数法和无量纲水头法，分析各琴键堰体型对淹没的敏感性，并在此基础上，拟合得到琴键堰的淹没流量折减系数公式，比较四种琴键堰在淹没出流条件下的泄流量和泄流效率，为完善琴键堰泄流理论，提升其设计水平以及推动其在渠道中的应用提供技术支撑。

1 琴键堰基本体型及研究方法

1.1 琴键堰基本体型

琴键堰的基本体型可以根据其倒悬的存在与否及具体位置分为四类：有对称上下游倒悬的A型琴键堰，只有上游或下游倒悬的B型和C型琴键堰，以及上、下游均没有倒悬的D型琴键堰（图1）。

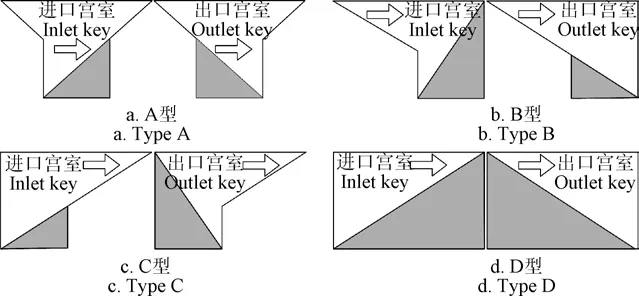
图1 琴键堰基本体型分类 Fig.1 Basic shape classification of Piano Key Weirs (PKWs)

琴键堰结构较复杂，体型参数众多，以A型琴键堰为例，其几何参数如图2所示，自由与淹没出流条件下的水力参数示意图如图3所示。

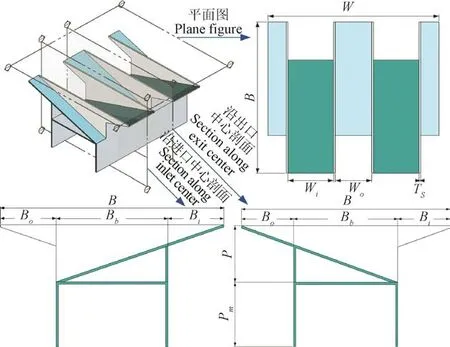
图2 琴键堰三维体型及几何参数 Fig.2 Three dimensional shape and geometric parameters of PKW

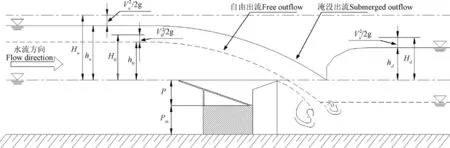
图3 琴键堰自由与淹没出流下的水力参数 Fig.3 Hydraulic parameters of PKW under free flow and submerged flow

1.2 堰后淹没流态划分

在给定某一来流量条件下，随着下游堰上水头H的增大，堰后一般会出现几种不同的淹没流态，这些流态基本分为：冲击射流、破碎（表面跳跃）、表面波和表 面射流，如图4所示（以薄壁堰淹没流态为例）。

图4 薄壁堰淹没流态分类 Fig.4 Classification of submerged flow pattern of sharp crest weir

冲击射流流态主要表现为过堰主流下潜，俯冲至渠道底部，并在堰后形成自上而下的卷气漩滚；而随着下游水位的抬升，由于受水流的顶托作用，碎波流态主要表现为在堰后下游的中层和表层产生的卷气漩涡；表面波和表面射流，则是由于下游水位的进一步增加而在渠道表面发生的大范围水面波动现象。

1.3 琴键堰淹没敏感性分析方法

本文分别采用Villemonte的流量折减系数法和Tullis等的无量纲水头法对比分析四种琴键堰对淹没的敏感性。

对于任何堰来说，在自由出流条件下，对于某一固定来流量，其堰上水头不随下游水位的变化而改变。而在淹没出流时，受下游水头H的影响，此时保持来流量不变，其上游水头会增加至H，说明在淹没情况下，要通过相同的来流量，则需要更高的上游堰上水头。

流量折减系数法用以描述在淹没出流条件下的流量折减系数C=Q/随淹没系数=H /H的变化关系。其中Q为淹没时上游固定来流量（m/s）；对于本文研究的四种琴键堰体型，我们在相同的上游固定来流量Q下，测量随着下游水位上升时H的变化情况，从而计算该水头下所对应的泄流量（m/s）。琴键堰泄流量计算如下式所示：

式中C为琴键堰泄流系数；为琴键堰上游堰上水头，m。

流量折减系数C主要与H /H有关，即

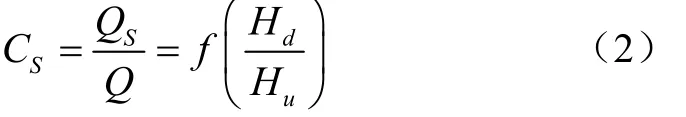
无量纲上下游水头法，则是利用自由出流条件下的上游堰上总水头，分别对淹没状态下的上下游水头进行无量纲化，计算琴键堰体型在淹没出流条件下的H /～H /曲线关系。

当下游水位抬升时，在低淹没水位下，下游水位不会影响自由流上游总水头，这种情况称为“模块淹没”。“临界淹没”定义为特定流量下琴键堰处于“模块淹没”和淹没出流的分界，而临界淹没度则对应于给定的泄流量下，由于下游水位的抬升而导致其上游压力水头读数的偏差不超过1%时的H /值，用S来表示。

2 试验设置与模型制作

2.1 试验水槽及数据测量

本研究所有琴键堰模型的过水试验在长16 m、宽0.5 m、深0.75 m的钢化玻璃水槽中进行。该水槽侧壁和槽底为厚度0.012 m的透明钢化玻璃，既确保了各流量工况下槽体的强度，又便于水流水力特性的观察和仪器测量。试验循环系统设备主要由水槽槽体、上游供水泵、电磁流量计流量测量设备、下游水位控制尾门以及下游回水设备组成。此外，在水槽内，距上游静水池1.0 m处配备了1 m长的孔式消流器，另接两层0.1 m厚的网式消流器，以消减上游水流紊动情况，保证均匀稳定的进水条件。琴键堰模型安装位置据上游消流装置7.5 m，距下游尾门4.5 m。水槽设施模型布置如图5所示。

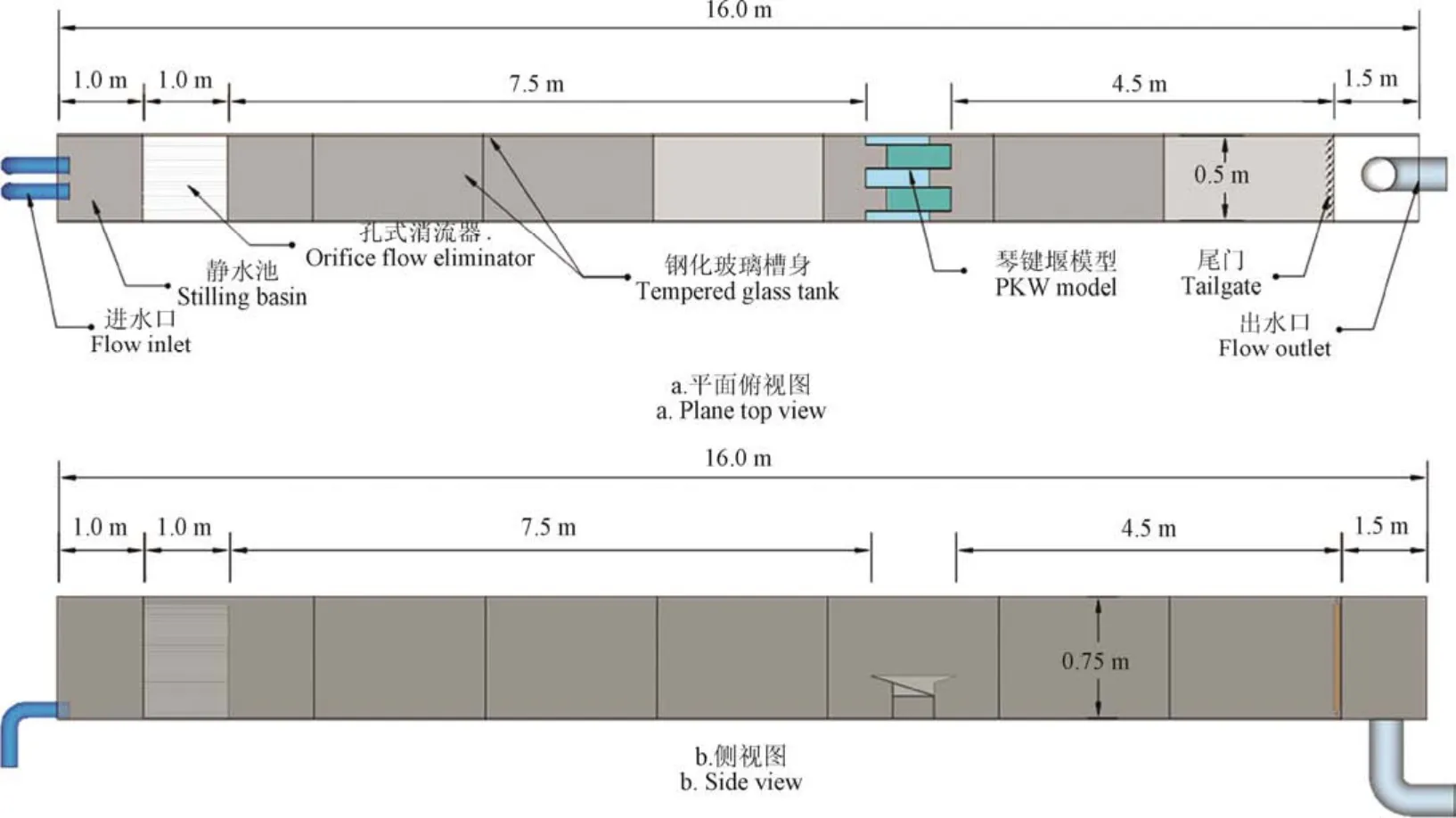
图5 试验水槽设施布置图 Fig.5 Layout of experimental flume facilities

对于流量的控制，实验室水槽系统配有电磁流量计，当流量≥0.05 m/s时，其精度为设定流量的1%；而当流量＜0.05 m/s时，其测量误差为0.000 5 m/s。水槽系统流量范围为0.001～0.110 m/s。上下游水位数据采用水位测针获取，上游水位测针放置在距琴键堰模型前1.8 m处，下游水位测针放置在琴键堰模型后1.5 m处。测量精度为：上游水位±0.000 1 m；下游水位±0.000 5 m，在靠近尾门处按有超声波水位计，作为下游水位的辅助测量。下游水位的控制通过不锈钢人字形尾门系统来实现，尾门开度的控制精度为0.1°。

2.2 琴键堰模型

试验中琴键堰模型（图6）选用厚度为0.005 m的有机玻璃制作，确保在试验的最大流量=0.110 m/s下不发生弯曲变形。琴键堰试验模型由两个进口和出口单元组成，所有琴键堰模型均设置相同高度的底座支撑。各体型几何参数及尺寸如表1所示。

图6 琴键堰试验模型 Fig.6 Test models of PKW

表1 琴键堰体型几何尺寸 Table 1 Geometric dimensions of PKWs m

3 试验结果与讨论

3.1 琴键堰淹没流态

当调节尾门开度使下游水位壅高从而影响到琴键堰上游堰上水头时，淹没发生。从琴键堰的出流特性来看，可以将琴键堰看做是向上游倾斜、向下游倾斜以及侧向的薄壁堰组合而成，而在观察琴键堰淹没出流试验过程中发现，随着下游水位的升高，四种不同体型琴键堰在堰后也都会依次出现上述几种淹没流态阶段。以A型琴键堰为例（图7），其淹没过程中的流态随下游水位的变化如下：1）下游水位不超过堰顶高程时，A型琴键堰处于自由出流状态。2）琴键堰淹没流态第一阶段为下游水位刚超过堰顶高程时，此时上游水流流经堰顶后钻入下游并向槽底俯冲，即呈现冲击射流状态（图7a），形成自槽底向下游表面的逆时针大范围卷气漩滚，而流经侧壁和出口的水流汇入出口宫室并沿向下的陡坡滑入下游渠道，因此与直线堰冲击射流淹没阶段的情形相比，该阶段琴键堰淹没流态的三维性更强，下游的漩滚范围更大，再加上其进口和出口宫室两股水流分别潜入下游尾水中层和底层，从而形成了自上而下的卷气漩涡，下游掺气非常充分。3）淹没流态第二阶段是尾水位进一步抬升时，流经琴键堰的水流受下游水位顶托作用，只在渠道表层及中层处形成小范围卷气漩涡，即碎波流态（图7b）。在冲击射流和碎波阶段，下游水流波动均发生在堰后约2倍堰高处，较远处水面相对平稳。4）随着下游水位继续上升，琴键堰过堰水流受高尾水位影响，基本无法掺入渠道中层和底层，在堰后依次呈现波动范围更长的表面波和表面射流流态，即为琴键堰淹没第三和第四阶段（图7c和7d）。从试验测量结果来看，堰后表面波和表面射流一直持续到下游约4～5倍的堰高处，此后为紊动表面射流。

图7 A型琴键堰淹没流态划分（来流量0.05 m3·s-1） Fig.7 Submerged flow pattern division of type A PKW (with an inflow of 0.05 m3·s-1)

此外，B型、C型和D型琴键堰也基本随着下游水位的增加逐渐呈现以上几个阶段的淹没流态，但因体型不同，每种琴键堰淹没阶段对应的下游水位也不相同。因此，对于每个琴键堰的临界淹没度、对淹没敏感性以及淹没条件下流量与上下游水位之间的关系，还需进一步系统分析。

3.2 不同类型琴键堰淹没敏感性分析

由琴键堰淹没出流试验数据，绘制四种琴键堰的流量折减系数C与淹没系数关系，如图8所示。

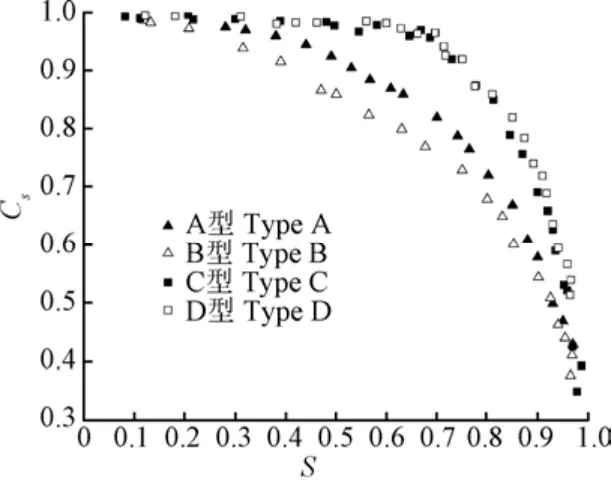
图8 四种琴键堰流量折减系数Cs与淹没系数S关系 Fig.8 Relationship between the flow reduction coefficient Cs and the submergence coefficient S of four types of PKWs

由图8看出，C型与D型琴键堰的试验条件下的流量折减系数分布较为接近。当＜0.6时，二者琴键堰的流量折减系数C值约等于1，意味着此时这两种琴键堰的上游水头不受下游水位的影响，均未发生淹没；当≥0.6后，C型和D型琴键堰逐渐发生淹没，其流量折减系数C值随淹没系数（=H /H）的增大而逐渐减小，表征了琴键堰随下游水位的抬升而淹没的程度增大。相对于C型和D型，A型与B型琴键堰会随着下游过堰水头的增加，提前开始淹没。当≥0.2和≥0.15时，A型和B型琴键堰的流量折减系数分别开始随淹没系数的增加而减小。对比这四种体型看来，C型和D型琴键堰对淹没的敏感性最低，其次是A型，而B型琴键堰最早发生淹没，对淹没最为敏感。

以上现象的原因有两方面：首先，对于B型琴键堰，其仅向上游倒悬，且该倒悬长度（B）为琴键堰总长的一半，因此，该体型的出口宫室坡度最缓，流经B型琴键堰出口宫室的水流在下游渠道中形成的跃后水深最小，相比于A型和C型琴键堰，跃后水深越小，对应的上游越前水深就越大，因此该体型的出口溢流前缘和侧面溢流前缘上游部分最先陷入局部淹没，对淹没最敏感；而对于A型琴键堰，其具有对称的上游倒悬和下游倒悬结构，悬伸长度（B和B）均占到总长的1/4，所以对淹没的敏感性仅次于B型；而C型与B型琴键堰相反，仅向下游倒悬，因此该型上游堰上水头最晚受到下游水位的影响。另外，除了出口宫室的影响，四种体型对应的进口宫室坡度也不同，水流从坡度最陡的B型琴键堰进口溢流前缘翻过时，受重力作用直接俯冲向下游渠道，并在堰后附近形成大范围旋滚，进一步抬高了下游水位，从而加剧了淹没的影响，而对于进口宫室坡度最缓的C型和D型琴键堰，流经进口宫室的水舌受水流惯性将下游水流推向距离琴键堰较远的位置，从而延缓了淹没的影响。

根据上图中四种琴键堰流量折减系数与淹没系数之间关系，利用多项式拟合，得到用于描述琴键堰在淹没出流条件下的流量折减系数的计算公式如下：

式中、、为拟合参数。

各体型琴键堰淹没流量折减系数拟合公式（1）中所对应的系数和相关参数见表2，拟合后四组方程的最大相对误差均在±5%以内。

表2 流量折减系数拟合公式的相关参数 Table 2 Relevant parameters of the flow reduction coefficient fitting formula

根据Tullis等在提出的无量纲上下游水头法，计算绘制四个琴键堰体型在淹没出流条件下的H /～H /关系，如图9所示。

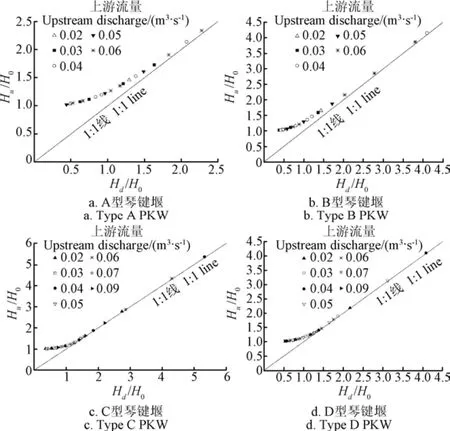
图9 恒定来流量下四种琴键堰无量纲水头Hu /H0与Hd /H0关系曲线 Fig.9 Dimensionless submerged head Hu /H0 and Hd /H0 relationships measured at constant discharges of four types of PKWs

分析图9可以发现，对于A型琴键堰，当H /＜0.5时，H /≈1，下游水深不影响上游水头，表明此时A型琴键堰处于“模块淹没”条件，当H /＞0.5后，H开始超过并逐渐增大（H /≥1），A型琴键堰进入淹没出流条件，也就是A型琴键堰的临界淹没度S为0.5。这意味对于A型琴键堰，当下游尾水总水头超过上游总水头的约50%时，下游尾水的淹没效应才会开始影响自由出流条件下的水头—流量关系。对于B型琴键堰，当H /＞0.3时就进入淹没出流条件，即该模型的临界淹没度S为0.3。而C型和D型琴键堰的无量纲淹没水头关系非常相近，分别在H /＜0.7（C型）和H /＜0.65（D型）时，二者上游堰上总水头H与自由出流时堰上总水头几乎相等；当H /＞0.7和H /＞0.65后，C和D型琴键堰进入淹没出流阶段（即C型和D型琴键堰的临界淹没度S分别为0.7和0.65）。

从图9还可以看出，对于A型和B型琴键堰，随着下游水头继续增加，当H /＞2.25和H /＞2.75后，两者的数据点基本都分布在H=H的正比例直线上，说明此后上下游堰上总水头大小始终保持相等，并同步增长。对于C型和D型琴键堰，当H /＞1.5后，两者的数据点也基本分布在H=H的正比例直线上，此时意味着琴键堰不再作为流量控制建筑物。

进一步绘制同一上游恒定来流量（以Q=0.06 m/s为例）工况下，四种琴键堰的无量纲上下游水头关系，如图10所示。

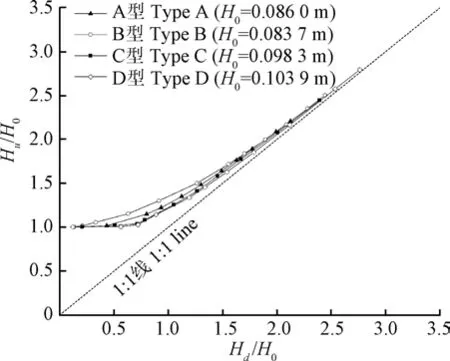
图10 四种琴键堰Hu /H0与Hd /H0关系对比 Fig.10 Comparison Hu /H0 and Hd /H0 relationships of four types of PKWs

对比可知，当下游水位一旦超过堰顶（即H＞0）时，随着H的增加，B型琴键堰最先受到淹没的影响，接着是A型，最后是C型和D型琴键堰。由此也可以说明，上游倒悬越长的琴键堰，其上游水头越容易先受下游水头的影响，而向下游的倒悬结构可以延缓上游的淹没。

3.3 淹没条件下不同类型琴键堰的水力性能

为了进一步对比不同类型的琴键堰在淹没出流条件下的泄流情况，在无量纲上下游水头H /～H /关系曲线的基础上，反算淹没条件下的上游水头，进而绘制四种不同琴键堰的反向无量纲上游水头/H与淹没系数H/H关系曲线，如图11所示。该琴键堰反向无量纲上游水头/H与淹没系数H/H之间的关系可通过如下指数关系给出（拟合公式中淹没系数＞S）：

图11 四种琴键堰H0/Hu与Hd/Hu之间的关系 Fig.11 Relationship between H0/Hu and Hd/Hu of four types of PKWs

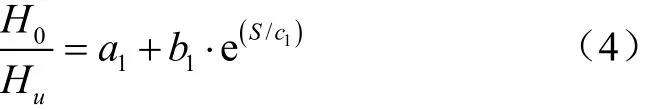
式中、、为拟合参数。对应的四种琴键堰的/H与H/H之间的指数关系拟合相关参数如表3所示。

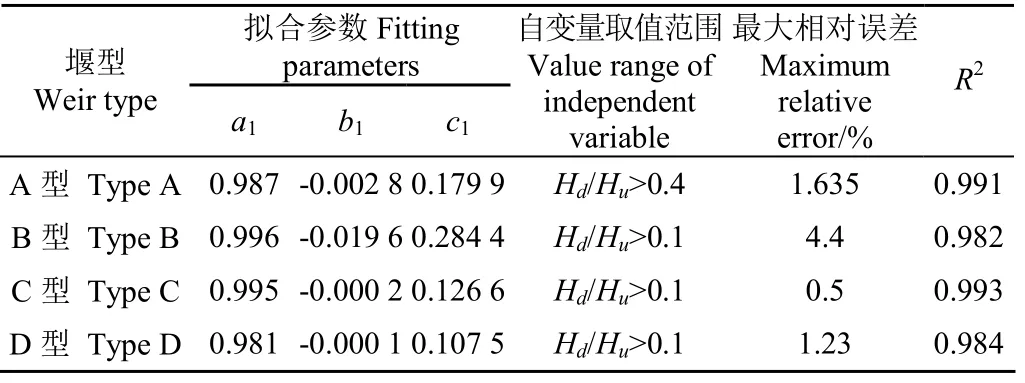
表3 反向无量纲上游水头拟合公式的相关参数 Table 3 Relevant parameters of the inverse dimensionless upstream water head fitting formula

进一步地，根据式（4）求出，再结合琴键堰泄流量计算公式和四种琴键堰在自由出流条件下泄流系数的拟合公式，用H和H的测量值得出淹没条件下的淹没流量Q（对应于反算出的淹没条件下的）。比较四种不同琴键堰在相同上游淹没水头条件下的泄流情况，如图12所示。

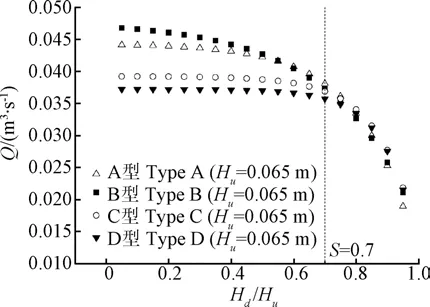
图12 四种琴键堰相同淹没水头下淹没泄流量比较 Fig.12 Comparison of submerged discharge of four types of PKWs under the same submerged water head

由图12可知，在上游淹没水头相同的的情况下，琴键堰的淹没泄流效率取决于淹没系数=H/H，即下游水位的变化。当淹没系数较小时，B型琴键堰的泄流量最大，这主要是因为在自由出流条件下，B型琴键堰具有最高的泄流效率，而当逐渐增大时，B型琴键堰的淹没泄流量最先开始减小，而A型琴键堰的泄流量也随之减小，但减小的幅度略小于B型琴键堰。此时B型琴键堰和A型琴键堰的淹没泄流量分别比D型琴键堰高约26%和19%。当=0.5时，该B型琴键堰的淹没泄流量已与A型淹没泄流量接近；＜0.6时，C型和D型琴键堰的淹没泄流量基本保持不变，而当0.6≤＜0.7时，这两种琴键堰淹没泄流量略有减小，但幅度很小。

而在≥0.7时，这四种琴键堰的淹没泄流量都随淹没度的增加而剧烈减小。且各类型琴键堰淹没泄流效率出现反向规律，即C型和D型琴键堰淹没泄流量逐渐超过A型和B型琴键堰。在这种情况下，式（4）已不适用，且此时淹没条件下的琴键堰水力性能也不能像自由流条件下的琴键堰一样简单归类，Cicero等将这种情形描述为综合效应，即当淹没系数大于一定值（各模型该淹没系数值不相等）时，琴键堰淹没泄流效率取决于其“对淹没的敏感性”和自由出流泄流效率两个方面的综合影响。考虑到在自由出流条件下，B型琴键堰具有最高的泄流效率，尽管该堰型容易受下游淹没的影响，但对于过流任务重且渠道宽度受限的工程，B型琴键堰仍然能在水力性能和施工成本中取得较好的平衡。A型琴键堰在自由出流条件时的泄流能力仅次于B型琴键堰，且在淹没度较低的淹没出流条件下时，也具有较高的泄流效率，再加上对称倒悬结构，使得A型琴键堰结构具有自平衡性质，因此在地形或施工条件（缆机长度的影响）受限的工程中，该堰型具有很大优势。C型和D型琴键堰一方面能有效延缓下游淹没的影响，另一方面仅向下游的倒悬结构也很有利于水上悬浮物（如浮木、草枝等）的通过，因此对于下游水位较高或有过木需求的工程，可以采用此类堰型，此外，这两类堰型也可以在渠道取水口处作为侧堰使用。

4 结 论

通过对四种琴键堰基本体型在淹没条件下的出流情况进行模型试验，得出了以下结论：

1）在淹没出流的情况下，随着下游水位的壅高，四种琴键堰均呈现出淹没后的冲击射流、碎波，表面波和表面射流四个阶段流态，但因体型不同，每种琴键堰各淹没阶段对应的下游水位也不相同。

2）对于四种不同体型的琴键堰，下游水位超过堰顶时逐渐开始发生淹没，分析四种琴键堰对淹没的敏感性发现，各类型琴键堰的临界淹没度分别为：B型0.3，A型0.5，C型和D型琴键堰则为0.7和0.65，即在来流量相同情况下B型琴键堰对淹没最敏感，A型琴键堰的敏感性低于B型，最后是C与D型琴键堰。从无量纲水头法和流量折减系数法对琴键堰的淹没出流的计算结果来看，不同琴键堰受下游水位的影响不同，主要是与各模型上下游的倒悬长度有关，上游倒悬越长，其出口宫室坡度越缓，越容易先发生淹没；另外进口宫室坡度最缓的C型和D型琴键堰，其流经进口宫室的水舌受在水流惯性的作用下，将下游水流推向距离琴键堰较远的位置，从而延缓了淹没的影响。

3）对于给定的上游水头，琴键堰的淹没泄流效率取决于下游水位的变化。对于选定的上游水头值，当淹没系数较小时，C型琴键堰和D型琴键堰的泄流效率分别低于A型，而B型的效率高于A型琴键堰。当淹没系数较大时，各体型琴键堰的泄流效率逐渐接近A型。而当≥0.7时，各类型琴键堰泄流效率出现反向规律，此时淹没泄流效率取决于“对淹没的敏感性”和自由出流泄流效率两个方面的综合影响。