橡胶-砂混合隔振材料初始变形模量试验研究

陈 佳， 庄海洋， 刘启菲， 吴 琪

(南京工业大学 岩土工程研究所，南京 210009)

近年来，随着我国汽车保有量的提高，废旧轮胎的数量快速攀升，据工信部报道仅2019年废旧轮胎产生量高达3.3亿条。由废旧轮胎切割所得的橡胶颗粒具有质量轻、耐磨性好、弹性高、价格低廉的特点，将其引入土木工程领域一方面可以实现资源的回收利用；另一方面可以改良土体的力学性能，在路基回填[1-2]、挡墙加固[3]、建筑抗震[4]和污水处理[5]中均有应用。

橡胶-砂混合隔振材料的初始变形模量是土体本构模型的主要参数，研究其变化规律对实际工程应用有着重要意义。近年来国内外学者对橡胶-砂混合料开展了一系列室内试验以探究混合料的静动力特性，其中有关初始变形模量的分析更多的集中在动力学试验，如动三轴试验[6-7]、循环单剪试验[8]、共振柱试验[9-11]以及弯曲元试验[12-14]。而静力学试验则较少，主要为直剪试验[15-16]和三轴试验[17-21]，Anvari等、Zornberg等和刘方成等通过不同的试验方法得出了一致的结论：橡胶-砂混合料的初始变形模量随橡胶含量的增加、相对密实度的降低、围压的降低而减小。然而目前初始变形模量的研究仍处于定性分析阶段，无法较好地指导工程实践。

基于上述原因，本文通过开展一系列三轴固结不排水试验，深入探究了橡胶-砂混合料初始变形模量E0随橡胶含量XC、粒径比d50,r/d50,s、相对密实度Dr以及围压σ3的变化规律，并给出了归一化的初始变形模量比E0/E0,XC=0的预测公式，以期为橡胶-砂混合料的实际应用提供可靠的设计依据。

1 试验方案

1.1 试验材料与试验设备

试验砂采用福建标准砂，经筛分后根据粒径范围分为：粗砂(1～2 mm)、中砂(0.25～0.50 mm)和细砂(0.075～0.250 mm)。橡胶颗粒选用由专业分解公司切割的废旧轮胎橡胶颗粒，其粒径范围为2～3 mm。试验材料的示意图和级配曲线如图1所示，基本物性指标如表1所示。

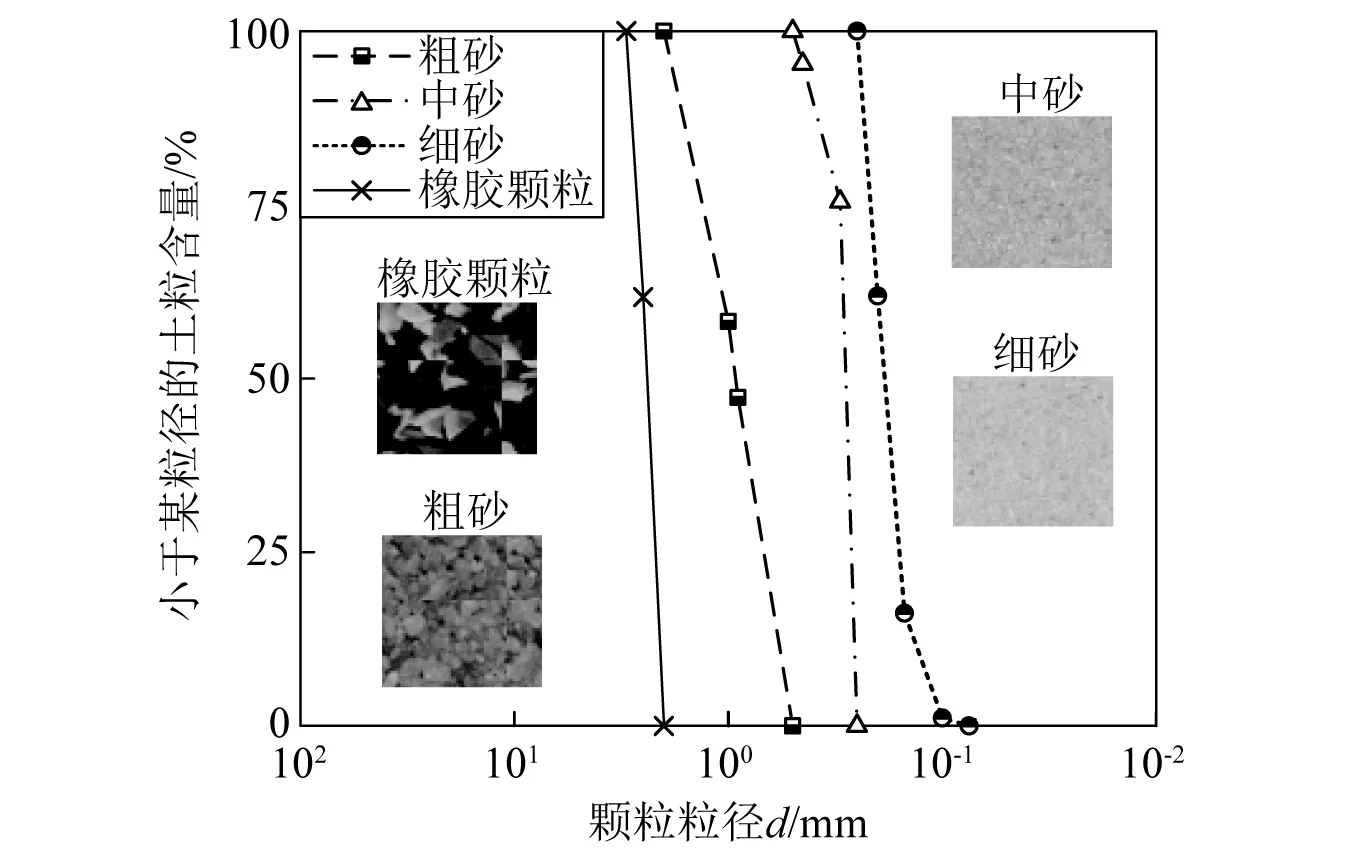
图1 级配曲线Fig.1 Grading curves

表1 橡胶-砂混合料基本物理特性指标Tab.1 The basic physical property index of rubber-sand mixture

试验所采用的仪器为南京工业大学岩土工程研究所购进的DYNTTS型GDS循环三轴仪。该仪器可以完成应变/应力控制的静、动三轴试验，本次试验使用应变控制进行静力加载。

1.2 试样制备与试验方法

试验试样为高100 mm，直径50 mm的实心圆柱形试样。由于橡胶颗粒与砂颗粒比重差异较大，常规砂雨法和水沉法易造成分层离析。而湿击法一方面可以利用水的吸附力使砂颗粒粘附在橡胶颗粒周围，从而实现两者的均匀混合；另一方面可以较好的控制试样的孔隙比e，同时也能获得较大的e值范围[22]。因此，本次试验采用湿击法制样。根据设定的相对密实度计算出所需的混合料质量，称取相应量的砂颗粒和橡胶颗粒，将其分成4等份，控制初始含水率为5%，将混合料拌合均匀后分4层夯实成样。

制样完成后，先向试样中通15 min CO2以除去试样内部空气，而后从试样底部通无气水直至试样顶部不再有气泡排出，预饱和完成后再对试样进行反压饱和。对饱和后的试样进行B值测定，若B>0.95，认为试样饱和完成，对试样进行均等固结。待试样变形及排水体积稳定视为固结完成，对试样进行不排水剪切试验，控制剪切应变速率为0.2 %/min。

1.3 试验方案

本次研究考察了6种橡胶含量、3种粒径比、3种相对密实度以及3种围压对橡胶-砂混合料初始变形模量的影响，均等固结不排水剪切试验方案如表2所示。其中XC表示橡胶颗粒在试样中所占质量比，d50,r/d50,s表示橡胶颗粒与砂颗粒的平均粒径之比。

表2 不排水剪切试验方案Tab.2 The undrained shear test condition

2 橡胶-砂混合料初始变形模量分析

在应变控制的CU试验中，保持围压σ3不变，通过仪器顶部传感器可获得轴向偏应力(σ1-σ3)。1963年Kondner通过对大量土三轴试验结果的分析，提出双曲线形式用以描述 (σ1-σ3)～ε1曲线[23]。

(1)

可将其改写为

(2)

式中:a为1/E0，E0为初始变形模量；b为通过试验数据得到的拟合参数。图2给出了橡胶-粗砂混合料的典型ε1/(σ1-σ3)～ε1曲线，如图2所示，在0～0.7%应变范围内，试样ε1/(σ1-σ3)与ε1呈明显线性，通过对该应变范围进行拟合，可得到试样的初始变形模量。

图2 三轴试验初始变形模量取值方法Fig.2 Initial deformation modulus in triaxial test

2.1 影响因素分析

图3为根据不同工况下橡胶-砂混合料由应力-应变关系曲线所确定的初始变形模量E0。由图3可知，随着橡胶含量XC的增加，混合料E0基本呈指数下降；围压越低，E0越小。考虑E0降低主要由橡胶颗粒与砂颗粒之间的刚度差异导致，相较于橡胶颗粒这一高弹性材料，砂颗粒在受力过程中几乎不发生体积压缩变形，可将视作刚性体。在混合料中，随着橡胶含量的增加，颗粒接触形式由以砂-砂颗粒间的刚性接触为主过渡到以橡胶-橡胶颗粒间的柔性接触为主，由此导致混合料的初始变形模量减小。

当粒径比d50,r/d50,s=2.6时，橡胶颗粒的加入会明显降低砂土的E0：当XC=10%时，E0降为纯粗砂的50%，而d50,r/d50,s=8.6和13.1时，相同的橡胶含量下初始变形模量仅衰减20%和30%。由此可见，d50,r/d50,s越小，少量橡胶颗粒的加入即可大大降低砂土的初始变形模量，即当橡胶与砂颗粒粒径越相近，橡胶颗粒的加入对土体整体力学性能的改变越大。这主要是因为在粒径比较小时，橡胶颗粒的少量加入置换出试样内部分砂颗粒，由砂-砂接触形成的有效传力路径被一部分橡胶-砂、橡胶-橡胶柔性接触截断，导致砂土初始变形模量的显著降低；而当粒径比d50,r/d50,s较大时，橡胶颗粒零星分布于砂颗粒内部，试样内部力链传递仍以砂-砂接触为主，加载过程中橡胶颗粒首先发生弹性变形，当体积无法继续压缩后，仍由砂颗粒之间的镶嵌咬合抵御剪应变的增大，故少量橡胶颗粒的加入对E0的衰减影响较小。

不同相对密实度下粗砂、细砂-橡胶混合料的初始变形模量如图4示。由图4可知，不同工况下的橡胶-砂混合料E0均随着相对密实度的增大而增大，且其增长速率随相对密实度的增加而有所减缓。这主要是由于相对密实度增大导致试样内部孔隙减小，颗粒间接触更为紧密，提高了橡胶-砂混合料的刚度；由于橡胶颗粒变形能力有限，当相对密实度继续提高时，橡胶颗粒将趋近于压缩极限，颗粒之间的咬合摩擦也将趋同，故继续增大相对密实度对初始变形模量的提高效果也将减缓。

图4 相对密实度对初始变形模量的影响Fig.4 Effect of relative density on initial deformation modulus

2.2 初始模量拟合

1963年Janbu提出，初始弹性模量E0与围压σ3有关，并给出如下的经验公式[24]

(3)

图5出了橡胶-砂混合料lg(E0/Pa)～lg(σ3/Pa)的关系，并采用Janbu给出的经验公式进行拟合。由图5可以发现，不同粒径比混合料得到的拟合直线规律基本一致，随着橡胶含量的增加，拟合线截距逐渐减小，但对斜率影响较小。将不同工况下由Janbu经验公式得到的拟合参数K和n绘于图6可以发现：K随橡胶含量的增加呈指数减小，中砂、细砂混合料得到的K随橡胶含量的衰减基本一致，而粗砂混合料得到的模量系数K明显更小，且随橡胶含量的变化所表现出来的非线性更强。当XC<30%时，对于不同粒径混合料，指数n变化范围较小，当XC=40%时，n表现出较大的离散性，呈快速增长趋势。指数n随XC的变化呈现较大离散性，说明橡胶-砂混合料作为一种新型回填料，其经验参数K和n的建议取值仍需要进行更多的试验探究。

图5 橡胶-砂混合料lg(E0/Pa)～lg(σ3/Pa)关系(Dr=50%)Fig.5 The lg(E0/Pa)-lg(σ3/Pa) curves of rubber-sand mixed soil (Dr=50%)

图6 拟合参数K和n(Dr=50%)Fig.6 Fitting parameters K and n(Dr=50%)

2.3 初始模量预测公式

为建立橡胶含量与初始弹性模量的关系，以对应围压下纯砂的初始变形模量为分母，统一对同一粒径比的E0进行归一化处理，图7出了归一化初始变形模量比E0/E0, XC=0随XC的变化规律及相应拟合曲线，可以发现，进行归一化处理后，基本消除了围压的影响，不同围压下E0/E0, XC=0基本趋于一致，可以采用如下的指数函数进行拟合

(4)

式中，k为试验拟合参数。

由图7可知，当d50,r/d50,s=2.6时，前期E0/E0, XC=0随XC的衰减较明显，当XC>20%后E0/E0, XC=0几乎不发生变化，归一化初始变形模量比呈明显非线性衰减；而粒径比增大后，E0/E0, XC=0的衰减趋于线性。将不同粒径比工况下拟合所得的参数k绘制于图8，可以发现k与粒径比存在明显线性关系，图中给出了两者间的经验公式，该公式的适用性仍需更多的试验进行验证。

图7 归一化初始变形模量随橡胶含量的变化(Dr=50%)Fig.7 Variation in normalized initial deformation modulus with rubber content(Dr=50%)

图8 拟合参数k与粒径比的关系Fig.8 Relationship between fitting parameter k and particle size ratio

为验证初始变形模量归一化研究思路的正确性，选用Lee等和姚玉文等弯曲元-伸缩元试验的试验结果，以对应围压下纯砂的初始剪切模量为分母，统一对同一粒径比的G0进行归一化处理，采用式(4)对G0/G0, XC=0随橡胶含量的变化进行拟合。如图9所示，由于试验所用的材料和橡胶掺入方式不同导致拟合参数k有所差异，但在不同橡胶含量下混合料的G0/G0, XC=0均呈良好的指数衰减趋势，拟合度较高，由此可见本文提出的归一化公式均具有较好的适用性。

图9 归一化初始模量预测公式验证Fig.9 Verification of the normalized initial modulus prediction formula

3 结 论

本文通过对橡胶-砂混合料进行不排水三轴试验，探究了橡胶含量、粒径比、相对密实度以及围压对混合料初始变形模量的影响，得到以下结论：

(1)橡胶-砂混合料的初始变形模量受橡胶含量影响较大，随着橡胶含量的增大呈指数下降；橡胶与砂颗粒粒径越接近时，橡胶颗粒的加入对土体整体力学性能的改变越大；初始变形模量随着围压和相对密实度的增大而增大，其增长速度随Dr增大而减小。

(2)采用Janbu经验公式得到的经验拟合系数K随XC的增大呈非线性指数减小；而得到的系数n离散性较大，仍需要更多的试验进行探究。

(3)本文提出采用对应围压下纯砂的初始模量进行试验结果归一化的研究思路，并给出归一化初始变形模量比E0/E0, XC=0的预测公式，并对公式进行了验证，为橡胶-砂混合料的工程应用及数值模拟提供了参考。