具有非线性刚度边界的杆梁结构的动态特性分析

许文峰， 唐 斌， BRENNAN Michael J.， MANCONI Elisabetta， GONÇALVES Paulo J. Paupitz

(1.大连理工大学 能源与动力学院，辽宁 大连 116024；2.圣保罗州立大学 工程学院，伊利亚索泰拉 15385-000；3.帕尔马大学 工程和建筑系，帕尔马 43100；4.圣保罗州立大学 工程学院，巴鲁 17033-360)

在工程领域中，很多实际结构都可以简化为线性连续结构的组合，例如弦、壳、杆和梁等[1-2]。道路维修时常用的钻地机通过杆状冲击钻不断冲击混凝土地面，达到迅速破坏路面的效果。涡轮机的叶片受到流体的冲击带动叶轮转动而产生动力。随着工程技术的发展，非线性边界对线性连续结构振动的研究逐渐提上日程，因为典型的线性刚度边界与理想约束边界[3]已经不能够满足工程需求。非线性因素的产生有许多原因，如接触碰撞中的间隙、干摩擦、材料弹塑性、构件大变形等。这些非线性因素的存在会使结构在较小的动态激励下产生线性系统所没有的现象，如分岔[4]、混沌[5]、超(亚)谐共振[6]等。除了受动态激励外，结构还有可能受到其他载荷，如重力、装配缺陷等引起的预载，这使结构表现出非常复杂的动态响应，其中最为典型的频域特征是随着激励频率的变化而产生“频率漂移[7]”和“跳跃[8]”现象。在复杂工况下，由过载引起的频漂将会导致非常严重的后果，这已引起工程技术人员的重点关注。

关于非线性刚度边界条件对连续杆梁结构动力特性的影响，在近半个世纪里也有一些研究进展。Tabaddor[9]从试验和理论两方面研究了悬臂梁在简谐外力激励下的单模态动力学特性。Gudmundson[10]用谐波平衡法分析了由非线性转动弹簧支承的均质梁的动力特性，确定了谐波和次谐波解是频率、激励幅值和材料阻尼的函数。Mei等[11]研究了波在Timoshenko梁中的反射和传播，导出了梁中各种不连续点的透射和反射矩阵。Mace[12]充分考虑了在梁的自由振动和受迫振动分析中，近场波与相邻不连续面相互作用的影响。Chouvion等[13-14]提出了一种用于三维波导结构振动分析的基于射线追踪法的通用波传播方法。Kovacic等[15]研究了非对称杜芬振子的主共振响应，对表明跳跃现象发生的多值解进行了理论计算和数值验证。Tang等[16-17]介绍了一种估算类达芬系统三次非线性刚度的试验研究方法，并对激振器-压缩梁耦合结构的振动试验数据进行了分析。Cremer等[18]提出了一种解决非线性边界问题行之有效的方法，即相位闭合原理。它的基本概念是：在一个完整的波传播回路中，一维结构中行波的总相变是2π的整数倍。

本文以非线性刚度弹簧固定的杆梁结构为研究对象，对比了采用相位闭合原理和分离变量法所得到的骨架曲线，并进一步得到结构的频响曲线，最后通过数值仿真验证了理论计算的准确性。

1 波在具有非线性刚度边界杆中的反射

图1为等截面均匀杆，右端通过非线性刚度弹簧固定。杆的长度为l，横截面积为S，杨氏模量为E，线密度为ρ，简谐激励振幅为Fl。弹簧具有线性和三次非线性刚度，分别为s1与s3。杆的位移为u(x,t)，设正方向向左，则弹簧力为f=-(s1w±s1w3)，式中：“+”为硬化弹簧；“-”为软化弹簧。设x=0处产生的纵向位移为U0，x=l处产生的纵向位移为Ul。

图1 连接非线性刚度弹簧的杆Fig.1 A rod connected to a nonlinear stiffness spring

1.1 自由振动

杆的运动微分方程为

(1)

边界条件是

(2)

入射波UIcos(ωt-kLx)与右端非线性边界发生碰撞后，将产生无数个奇数倍频率的反射谐波。由于本文考虑的非线性程度相对较弱，反射能量主要集中在一次反射谐波，所以在下文分析中，忽略高次反射谐波影响。

采用行波法表示杆中任意一点的纵向位移

u(x,t)=UIcos(ωt-kLx)+URcos(ωt+kLx+φL)

(3)

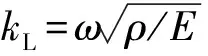
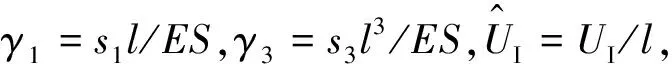
(4)

为了方便分析，本节的后续计算都以硬化弹簧为例进行求解。

联立式(2)和式(3)，采用谐波平衡法，无量纲化得

ΩLtan(φL/2)=1+3γ行波[1+cos(φL)]/2

(5)

式中，ΩL=ESkL/s1为边界处线性刚度的阻抗模量等于杆的阻抗时的频率。

由图1可知，杆左端是自由边界，相位变化是0；右端是非线性边界，设相位变化是φL。因此根据相位闭合原理有

2kLl-0-φL=2nπ(n=0,1,2,…)

(6)

式中，kLl=γ1ΩL。

故式(5)可化简成

ΩLtan(kLl)=1+3γ行波[1+cos(2kLl)]/2

(7)

采用分离变量法[19]表示杆中任意一点的纵向位移

u(x,t)=U(x)cos(ωt+φ)=

[Acos(kLx)+Bsin(kLx)]cos(ωt+φ)

(8)

式中：U(x)为杆中任意一点x的最大振幅；A和B为根据边界条件确定的常数。

将杆的位移式(8)代入边界条件式(2)，并注意到cos3(x)=[3cos(x)+cos(3x)]/4，无量纲化得

ΩLtan(kLl)=1+3γ分离/4

(9)

比较式(7)和式(9)，可以得出行波法与分离变量法之间的联系

(10)

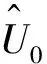
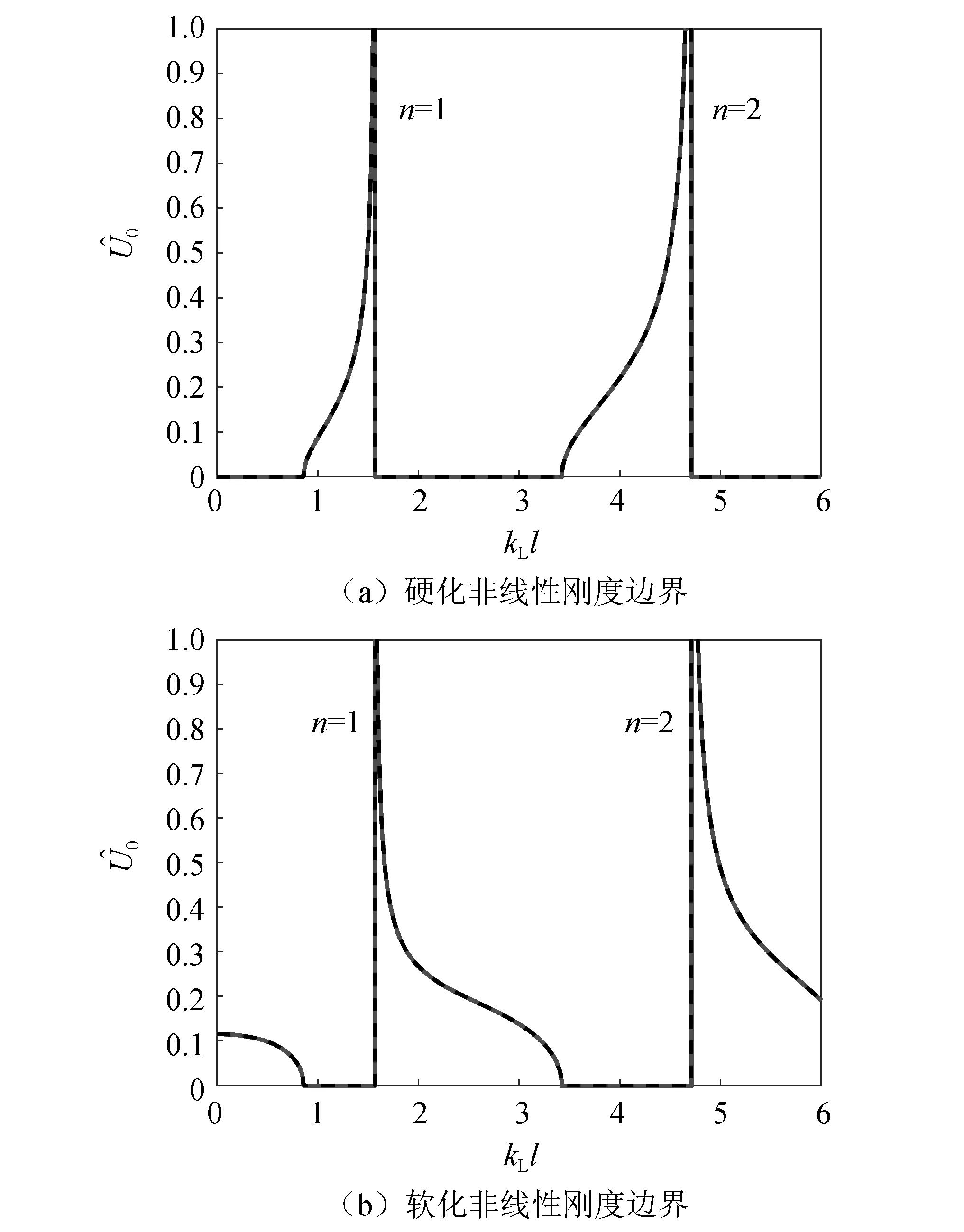
图2 杆的骨架曲线Fig.2 The backbone curves of the rod

1.2 强迫振动

在杆的自由端施加一个简谐激励Flcos(ωt+φ)，采用分离变量法表示杆中任意一点位移。

此时的边界条件为

(11)

将杆的位移表达式(8)代入边界条件式(11)，无量纲化得

(12)

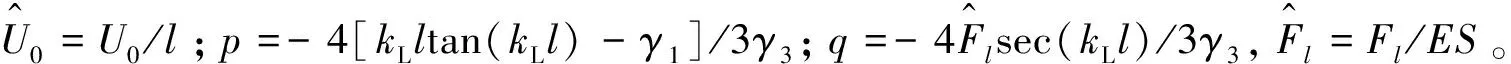
图3 杆的频响曲线Fig.3 The frequency response curve of the rod

1.3 数值仿真验证

采用有限元方法对上述理论分析得到的频响曲线进行数值仿真验证。设细长圆杆的参数为l=1 m，R=0.01 m，ρ=7 850 kg/m3，E=2×1011Pa，S=3.14×10-4m2。简谐激励的幅值为Fl=6.28×106N，边界处的非线性刚度参数为s1=6.28×107N/m，s3=6.28×109N/m3。将杆离散为100个单元。在跳频点附近进行正扫频与负扫频，扫频频率间隔最小为0.05 Hz。

理论解与有限元方法得到的仿真解，如图4所示。由图4可以看出，两种方法的计算结果基本吻合。

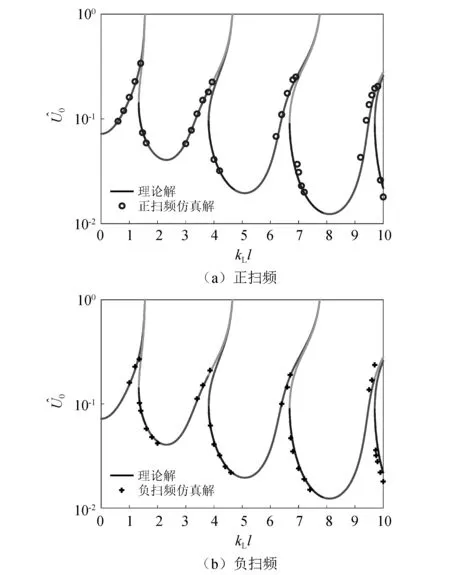
图4 杆的频响曲线对比图Fig.4 Comparison of the frequency response curve of the rod

2 波在具有非线性刚度边界梁中的反射

图5为等截面均匀梁，其右端通过非线性刚度弹簧固定。梁的长度为l，横截面积为S，杨氏模量为E，线密度为ρ，简谐激励振幅为Fl。弹簧具有线性和三次非线性刚度，分别为s1与s3。梁的位移为w(x,t)，设正方向向上，则弹簧力为f=s1w±s1w3，式中：“+”为硬化弹簧；“-”为软化弹簧。设x=0处产生的横向位移为W0，x=l处产生的横向位移为Wl。

2.1 自由振动

梁的运动微分方程

(13)

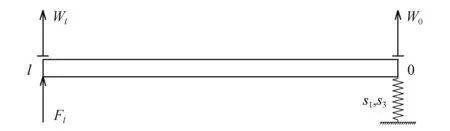
图5 连接非线性刚度弹簧的梁Fig.5 A beam connected to a nonlinear stiffness spring

边界条件为

(14)

(15)

入射传递波WIPcos(ωt-kFx)与右端非线性边界发生碰撞后，将产生无数个反射传递波与反射近场波。考虑到反射能量主要集中在一次反射谐波，因此忽略高次反射谐波的影响。

设梁中任一点处的横向位移为

w(x,t)=WIPcos(ωt-kFx)+WPPcos(ωt+kFx+φPP)+
WNPekFxcos(ωt+φNP)

(16)

式中：WIP为入射波振幅；WPP为反射传递波振幅；WNP为反射近场波振幅；φPP为反射传递波相位；φNP为反射近场波相位；kF=ω1/2(ρA/EI)1/4为横波波数。

联立式(14)、式(15)和式(16)，无量纲化得

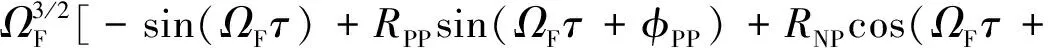
(17)

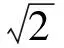
使用一阶谐波平衡法求解式(17)可得

tan(φNP)=sin(φPP)/[1+cos(φPP)]

(18)

RNP=sin(φPP)/sin(φNP)

(19)

(20)

记h(x)=cos(x)+RPPcos(x+φPP)+RNPcos(x+φNP)，采用包络线的计算方法，由梁的位移式(16)可得

(21)

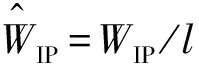
联立式(18)～式(21)，可以得到传递波入射时，硬化与软化边界条件下非线性边界对梁振动的影响[20]。

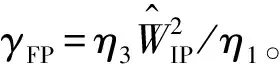
2kFl-(-π/2)-φPP=2nπ(n=0,1,2,…)

(22)

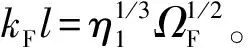
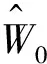
令η1=10，η3±1 000将相位闭合原理与分离变量法(计算公式见2.2节)得到的骨架曲线进行对比，如图6所示。其中，实线为相位闭合原理计算结果，虚线为分离变量法计算结果。由于相位闭合原理忽略了近场波，低频时近场波幅值衰减得相对更慢，因此在低频(低于自由-铰支梁的第一阶固有频率)范围内存在一定误差。

入射近场波WINe-kFxcos(ωt)与右端非线性边界发生碰撞后发生反射。同样地，忽略高次反射谐波。

设梁中任一点处的横向位移为

w(x,t)=WINe-kFxcos(ωt)+WPNcos(ωt+kFx+φPN)+
WNNekFxcos(ωt+φNN)

(23)

图6 梁的骨架曲线Fig.6 The backbone curves of the beam

联立式(14)、(15)和式(23)，无量纲化得

(24)

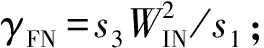
使用一阶谐波平衡法求解可得

RPN=2sin(φPN)

(25)

tan(φNN)=RPNsin(φPN)/[RPNcos(φPN)-1]

(26)

RNN=RPNsin(φPN)/sin(φNN)

(27)

Ω3/2=[2+24γFNsin(φPN)2]/[1-cot(φPN)]

(28)

联立式(25)～式(28)，可以得到近场波入射时，硬化与软化边界条件下非线性边界对梁振动的影响。

2.2 强迫振动

在梁的自由端施加一个简谐激励Flcos(ωt+φ)，采用分离变量法表示梁中任意一点的位移。

设梁中任一点处的横向位移为

w(x,t)=W(x)cos(ωt+φ)

(29)

式中，W(x)=c1cosh(kFx)+c2sinh(kFx)+c3cos(kFx)+c4sin(kFx)，而c1,c2,c3,c4需要根据边界条件确定。

此时的边界条件为

(30)

(31)

将位移式(29)代入以上边界条件中，可以解得系数c1,c2,c3,c4。此时可得处的最大横向位移为

W0=W(0)=c1+c3=

(32)

记M=cos(kFl)sinh(kFl)-cosh(kFl)sin(kFl)，N=cos(kFl)cosh(kFl)-1，则式(32)可整理成关于W0的三次多项式

(33)

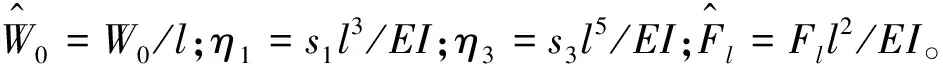
将式(33)的三次项系数化简为1，得

(34)

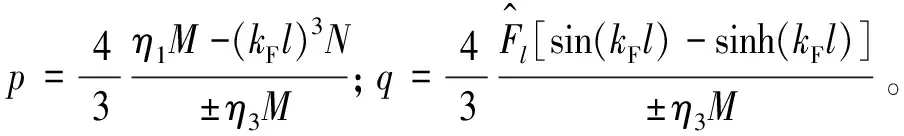
若Fl=0，则式(33)转变为梁的骨架曲线

(35)

2.3 数值仿真验证

采用有限元方法对上述理论分析得到的频响曲线进行数值仿真验证。设梁的参数为l=1 m，R=0.01 m，ρ=7 850 kg/m3，E=2×1011Pa，S=3.14×10-4m2。简谐激励的幅值为Fl=1 570.80 N，边界处的非线性刚度参数为s1=1.57×104N/m，s3=1.57×106N/m3。将梁离散为100个单元。在跳频点附近进行正扫频与负扫频，扫频频率间隔最小为0.05 Hz。

理论解与有限元方法得到的仿真解，如图8所示。由图8可以看出，两种方法的计算结果基本吻合。

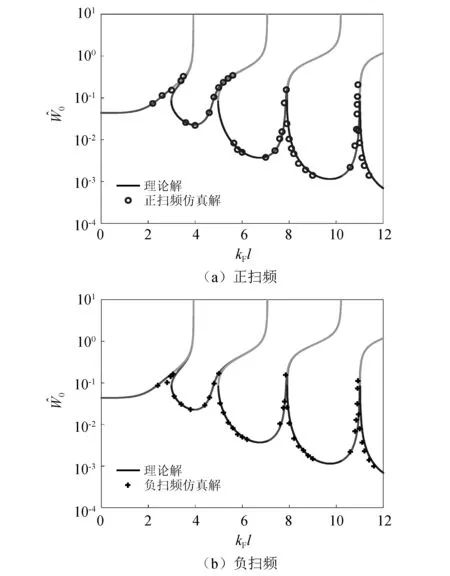
图8 梁的频响曲线对比图Fig.8 Comparison of the frequency response curve of the beam

3 结 论

本文以具有非线性刚度边界的杆梁结构为研究对象，建立了行波法与分离变量法的联系，确定了结构自由振动时无量纲频率、振幅和反射系数等参数之间的关系，得到了杆梁结构的骨架与频响曲线。

通过理论分析与数值仿真，得到如下结论：

(1) 应用相位闭合原理与分离变量法得到的杆梁的骨架曲线基本一致；但是，在低频范围内，由于相位闭合原理忽略了近场波的影响，计算得到的梁结构的骨架曲线与分离变量法的结果存在一定差异。

(2) 使用有限元方法进行了数值仿真分析，进而对非线性跳频现象进行了验证。仿真结果与分离变量法得到的频响曲线吻合较好。