基于SSWPT边际谱特征信息提取的齿轮故障诊断
2022-08-05唐贵基徐振丽
唐贵基, 徐振丽, 庞 彬, 白 洁
(1. 华北电力大学 河北省电力机械装备健康维护与失效预防重点实验室,河北 保定 071003;2. 河北大学 质量技术监督学院,河北 保定 071002)
齿轮作为旋转机械设备的关键部件,在机械设备运行中发挥着传递动力的重要作用,其运行状态好坏直接影响整个机械设备的稳定性。统计数据表明,齿轮故障是造成旋转机械设备发生停机等事故的主要原因之一。因此,及时发现齿轮故障并对其进行诊断具有重要意义[1]。
当齿轮发生故障时,采集的振动信号通常呈现出强烈的非平稳特性以及调幅调频特性[2]。识别啮合频率附近的故障特征边带是实现齿轮故障诊断的关键。然而,在实际运行中,由于大多数齿轮受到各种因素的干扰,引起的啮合调制频带十分复杂,仅通过频谱分析难以直接识别齿轮故障振动信号的特征边带。基于解调分析的故障诊断方法使故障特征频率可以在包络谱中突出显示,为齿轮故障特征提取提供了一种有效策略。近年来,许多学者对解调方法开展了大量研究[3-5]。其中,常用的解调方法主要有Hilbert解调和能量算子解调。但是,上述方法仅适用于单分量信号,对多分量信号应用解调算法之前需要进行带通滤波,将多分量信号进行分离。然而,传统的滤波器的中心频率及带宽需要人为设定,具有很大的局限性。为解决上述问题,Antoni等[6]提出了快速谱峭方法,有效地解决了带通滤波器中心频率和带宽参数的确定。文献[7]将该算法用于确定滤波器的参数并进行带通滤波和解调分析,成功提取出轴承故障特征频率。此外,经验模态分解(empirical mode decomposition,EMD)[8]、局部均值分解(local mean decomposition,LMD)[9]以及变分模态分解(variational modal decomposition,VMD)[10]等方法被用于故障振动信号分解,将多分量的振动信号分解为具有故障特征信息的单分量信号,然后通过解调算法提取故障特征频率。文献[11]将LMD方法应用到齿轮故障诊断中,证明了该方法在提取齿轮故障特征方面的优越性。文献[12]借鉴HHT(Hilbert-Huang transform)的思路,定义了LMD边际谱的概念,并将该方法用于滚动轴承实际故障诊断中,成功提取了轴承故障特征频率。杨宇等[13]将VMD方法应用到齿轮复合故障诊断中,有效抑制了频率混叠现象,为齿轮复合故障诊断提供了依据。尽管上述分解方法在机械故障诊断中得到了广泛应用,但这些方法均存在不足。EMD方法存在模态混叠、端点效应等问题,严重影响到故障诊断的精度;LMD方法计算效率较低;VMD方法缺乏严格的理论基础支撑。
同步压缩小波包变换(synchrosqueezed wave packet transform,SSWPT)是最近发展起来的一种新的信号处理方法,该方法是同步压缩变换(synchrosqueezing trannsform,SST)与小波包变换的结合,能够准确提取信号的瞬时信息,具有良好的抗噪性能,适用于非线性、非平稳的振动信号分析。目前,该方法在医学信号处理方面取得了一定的成果。基于以上分析,本文借鉴Hilbert边际谱的思想,给出了SSWPT边际谱的计算公式。将SSWPT边际谱应用于齿轮故障诊断中,通过仿真及试验分析证明了该方法的有效性。
1 同步压缩小波包变换原理
SSWPT利用小波包变换后信号的相位信息不受尺度变化影响的特性求取各尺度下的瞬时频率,然后将同一尺度下的瞬时频率进行累加,对重新分配的小波包变换系数进行压缩,从而将相同频率附近的值压缩至该频率中,提高了时频分辨率。
1.1 小波包变换
选择一个母波包w(x)与缩放参数s共同定义一个紧凑支撑的小波包族
(1)
式中:a为小波包族的尺度因子,|a|≥1;b为平移因子,b∈R;s为缩放参数。文献[14]表明:当s<1.0时,SSWPT可以更好地区分频率相近的分量;当s>0.5时,小波包可以充分局部化,SSWPT得到更精确的瞬时频率;因此,s的范围为(0.5,1.0),本文取s=0.51。
小波包族的傅里叶变换表示为
(2)
对任意信号f(x)∈L2(R),其小波包变换表示为
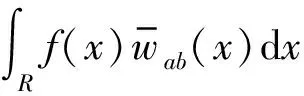
(3)
式中,Wf(a,b)为小波包变换系数。
1.2 同步压缩小波包
通过对信号进行小波包变换后可以得到小波包变换系数,此时可求取瞬时频率
(4)
最后根据计算得到的瞬时频率,建立(b,a)~[b,vf(a,b)]的映射关系,将小波包系数从时间—尺度平面转化到时间—频率平面,将信号中各频率成分沿频率域方向进行压缩,提高了小波包在频率域上的分辨率。同步压缩小波包能量的表达式可以表示为

(5)
式中: δ为狄拉克函数; Revf(a,b)为瞬时频率的实部;v为信号的中心频率。
SSWPT不仅具有较高的时频分辨率,还支持信号的重构。通过同步压缩能量分布图选取K个需要重构的频带的数量,将能量矩阵划分为K个族{U1,U2,…,UK},其中每个族称为一个本征模态函数,最后通过信号的重构恢复其每个本征模态函数,其同步压缩小波包逆变换(synchrosqueezed wave packet inverse transformation,ISSWPT)表达式为
(6)

(7)

综上所述,基于同步压缩小波包变换的步骤如下:
步骤1利用小波包变换求取小波包变换系数Wf(a,b)和主偏导∂bWf(a,b);
步骤2计算瞬时频率vf(a,b),并进行同步压缩小波包变换得到同步压缩小波包能量Tf(v,b);
步骤3选择感兴趣的频带范围,运用ISSWPT进行信号的重构。
2 基于SSWPT边际谱特征提取
2.1 基于SSWPT边际谱原理
本文在同步压缩小波包变换的基础上,借鉴Hilbert边际谱的思想,定义基于SSWPT的边际谱为
(8)
边际谱中的幅值大小为某频率分量在各个时刻的幅值之和。因此,边际谱反映了信号的幅值在整个时间尺度上随频率变化的情况。当齿轮发生故障时,其振动信号呈现调制特征,通过信号处理方法对齿轮故障频率进行识别,可实现齿轮故障诊断。因此,本文利用SSWPT边际谱特征提取方法对齿轮振动信号进行分析,提取故障特征频率。
2.2 啮合调制频带重构
运用ISSWPT进行信号重构时,重构频带范围的选取对重构效果有很大的影响。Kong等[15]通过对啮合调制频带重构成功提取齿轮故障特征频率,证明了啮合调制区域中包含大量齿轮故障特征信息。因此,本文根据SSWPT边际谱确定啮合频率及其倍频,并选择以K×fm为中心频率、以a×fr(a∈Z)为半带宽构成啮合调制频带的范围,即:UK=[K×fm-a×fr,K×fm+a×fr],根据啮合调制频带范围,通过式(7)对SSWPT能量矩阵逆变换进行信号重构,根据重构信号的包络谱判断齿轮的健康状态。文献[16]指出,在分析振动信号时选择的半带宽至少为故障特征频率的3倍以上,以确保信号包含足够的特征信息。因此,本文重构频带的范围选择以高速轴转频的3倍为半带宽。其中:K为边际谱提取的啮合调制频带数量,即取值为边际谱中包含的啮合频率的倍频数;fm为啮合频率;fr为高速轴转频;a=3。
2.3 算法流程图
本文提出基于SSWPT边际谱特征信息提取的齿轮故障诊断方法,其技术路线如图1所示,具体步骤如下:
步骤1对齿轮故障振动信号进行SSWPT,得到振动信号的能量分布图;
步骤2对振动信号的能量矩阵进行积分处理,求取振动信号的边际谱,提取信号的啮合频率及其倍频;
步骤3选择对应的啮合调制频带,根据啮合频带的范围,通过ISSWPT对能量矩阵重构信号;
步骤4将步骤3中的重构信号进行包络分析,从而根据包络谱中故障特征频率对齿轮进行故障诊断。

图1 SSWPT边际谱特征提取方法Fig.1 SSWPT marginal spectrum feature extraction method
3 仿真分析
为验证本文方法的有效性,首先对含高斯白噪声(式(9))的仿真信号x(t)进行分析处理
(9)
式中:x1(t)和x2(t)为两个调幅调频信号;n(t)为高斯白噪声;s(t)为干扰信号。仿真参数如表1所示。

表1 仿真参数Tab.1 Parameters of simulated signals
仿真信号的采样频率fs=1 024 Hz,任意选取 4 096个连续的数据点进行分析。图2为该仿真信号的时域波形及频谱。从图2(a)可知,时域图中的冲击成分被强背景噪声淹没,不能提取有效的信息;从图2(b)可知,频谱图中存在大量的噪声及干扰成分,仅根据频谱分析不能有效的提取故障特征信息。

图2 仿真信号的波形及频谱Fig.2 Waveform and spectrum of simulated signals
将仿真信号按照图1所示流程图,将仿真信号首先进行SSPWT分析,其能量分布图如图3(a)所示。由图3(a)可知,能量主要集中在瞬时频率为100 Hz和200 Hz周围,瞬时频率存在波动现象,且幅值大小不均匀,反映了瞬时频率存在调频特性。根据式(8)将SSWPT能量图变换为边际谱,结果如图3(b)所示。由图3(b)可知,边际谱中各频率成分谱线清晰,幅值突出。
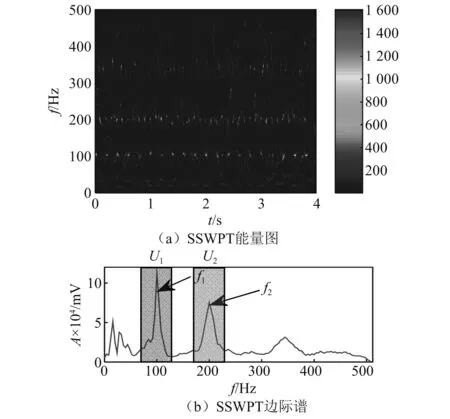
图3 仿真信号的SSWPT能量分布及边际谱Fig.3 SSWPT energy distribution and marginal spectrum of simulated signals
为了进一步证明SSWPT边际谱在特征提取方面的优越性,根据文献[17]提出的频率特征比指标来选择最优品质因子Q,本文引入特征能量比(features energy ratio,FER)指标来定量衡量特征提取效果。特征能量比定义为故障频率的能量与所有频率总能量的比值,其计算公式为
(10)
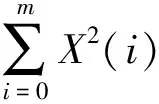
将SSWPT边际谱方法与SSWPT谱方法进行定量对比分析,评价结果如表2所示。由表2可知,SSWPT边际谱的特征能量比最大,证明了SSWPT边际谱的特征提取效果优于SSWPT谱。

表2 特征能量比Tab.2 Features energy ratio
根据SSWPT边际谱确定中心频率f1和f2,并以此为中心,以3fr2为半带宽构成啮合调制频带U1和U2。根据两个频带的范围将能量矩阵按照式(7)分别进行重构。频带U1和U2重构信号的时域波形及包络谱,分别如图4和图5所示。从图4(a)和图5(a)可知,时域波形中信号的周期性冲击特征增强,重构效果良好。对重构信号进行包络谱分析,结果如图4(b)和图5(b)所示。从包络谱中可以发现调制频率及倍频处幅值突出,无关干扰成分被有效滤除。通过仿真分析进一步验证了该方法的有效性。

图4 重构信号的波形及包络谱Fig.4 Waveform and envelope spectrum of reconstructed signal

图5 重构信号的波形及包络谱Fig.5 Waveform and envelope spectrum of reconstructed signal
4 试验分析
试验采用从Amirkabir理工大学设计的变速箱中采集的振动信号对该方法的有效性进行验证。在图6所示的试验台模拟了主动轮正常及发生断齿和磨齿不同故障类型的振动信号。试验装置包括电动机、加速度计、齿轮箱及模拟数字转换器。变速箱由标称转速为1 420 r/min的三相电动机驱动,主动轮齿数为15,从动轮齿数为110。由于工况变动与负载变化的影响,通过频谱分析得到故障齿轮的实际转频fr=24.33 Hz,对应的啮合频率为365 Hz。振动信号由安装在齿轮箱上的加速度计采集,信号采样频率fs=10 kHz。本文选择对断齿和磨齿两故障类型的实测信号进行分析,分析点数为8 192。

图6 试验平台Fig.6 Experimental platform
4.1 断齿故障分析
断齿故障时齿轮振动信号的波形及频谱图,如图7所示。时域波形中周期性冲击特征不明显,齿轮的故障特征被强噪声淹没。从频谱图可以观察到齿轮的啮合频率,且幅值比较突出,但啮合调制频带存在频率混叠现象,难以检测到故障齿轮的转频信息。当断齿发生故障时,齿轮振动信号的包络谱如图8所示。包络谱中可发现齿轮故障特征频率及倍频。但包络谱中较多的干扰成分,这些干扰成分对于齿轮状态的识别造成较大的影响,容易导致漏诊或误诊。
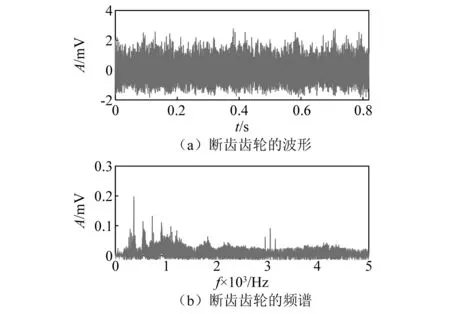
图7 断齿齿轮信号的波形及频谱Fig.7 Waveform and spectrum of broken tooth gear
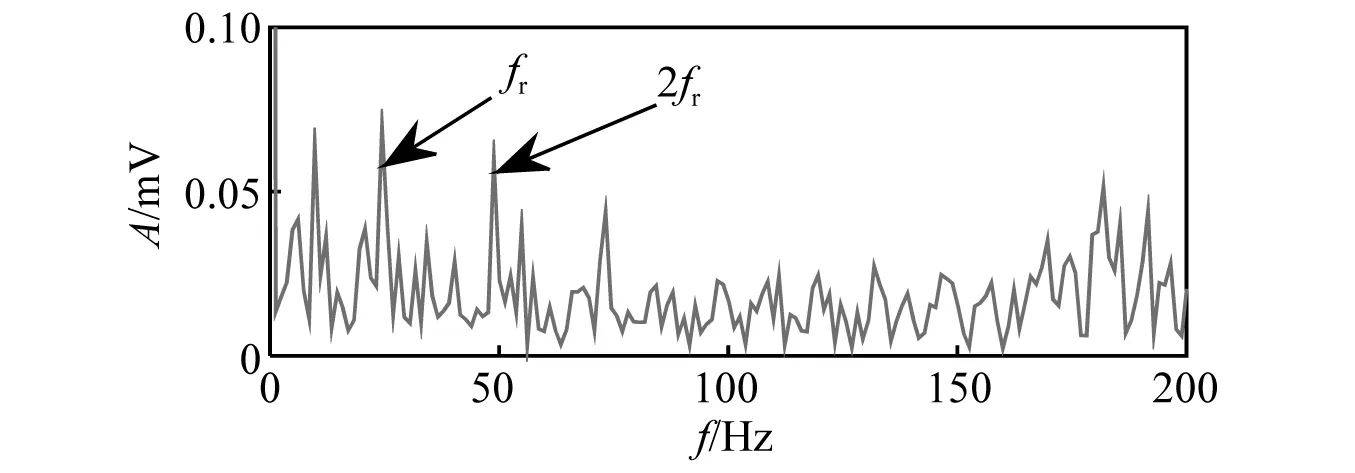
图8 断齿齿轮信号的包络谱Fig.8 Envelope spectrum of broken tooth gear
为进一步提取齿轮故障的特征频率,采用本文所提方法分析该齿轮故障的振动信号。图9(a)为对故障齿轮振动信号进行SSWPT得到的能量分布图。利用时频分析结果,进一步求取故障振动信号的边际谱,结果如图9(b)所示。图9中各频率分量的幅值谱线清晰,可以清晰的提取1倍和2倍啮合频率。因此,根据SSWPT边际谱提取啮合频率fm和2fm并以此为中心频率,以3fr为半带宽构成啮合调制频带U1和U2。

图9 断齿齿轮的SSWPT能量分布及边际谱Fig.9 SSWPT energy distribution and marginal spectrum of broken gear
根据啮合调制频带U1和频带U2的范围,对能量矩阵运用ISSWPT重构信号。啮合调制频带U1重构信号的时域波形及包络谱,如图10所示。由图10可知,时域图中重构信号的冲击成分明显增多,具有一定的规律性。包络谱中输入轴的转频及其倍频成分处的幅值谱线十分明显,因此很容易判别出主动轮发生了故障。

图10 重构信号的波形及包络谱Fig.10 Waveform and envelope spectrum of reconstructed signal
图11(a)为啮合调制频带U2重构信号的时域波形,通过与图7对比可知,时域图中齿轮故障振动信号的周期性特征明显增强。对重构信号做进一步包络谱分析结果如图11(b)所示。图中主动轮所在轴的转频及转频的倍频处幅值谱线突出。综上所述,同步压缩小波包变换具有良好的重构能力及降噪性能,能够有效提取齿轮故障特征信息,识别齿轮故障。

图11 重构信号的波形及包络谱Fig.11 Waveform and envelope spectrum of reconstructed signal
为了进一步验证本文方法的优势,利用快速谱峭度方法对该试验信号进行对比分析,其结果如图12(a)所示。通过快速谱峭度方法可以快速筛选出齿轮故障振动信号的最大峭度频带,并对提取的频带进行平方包络谱分析结果如图12(b)所示。由图12(b)可知,平方包络谱中只能提取微弱的2倍转频,其余故障特征频率被大量噪声及干扰成分淹没。表3为本文所提方法与包络谱、基于快速谱峭度方法的定量分析结果。由表3可知,本文所提方法的齿轮故障特征频率比重较大,证明了该方法可以有效的提取齿轮故障特征频率,判别齿轮故障。

图12 断齿故障信号的快速谱峭度分析Fig.12 Fast spectral kurtosis analysis of broken tooth fault signal

表3 特征能量比Tab.3 Features energy ratio
4.2 磨齿故障分析
齿轮发生磨齿故障时振动信号的时域波形及频谱图如图13所示,包络谱如图14所示。由图14可知,包络谱中可发现微弱的齿轮故障特征频率,由于干扰成分较多,不利于齿轮故障特征的识别。图15~图17是通过本文方法的分析结果。本文方法得到的边际谱谱线清晰,啮合调制频率及其倍频易观察,重构信号的时域波形冲击性更强。由表4可知,本文所提方法的齿轮故障特征频率能量比较大,进一步证明了该方法的有效性。从重构信号的包络谱中可以精确提取齿轮故障特征频率,有效识别主动齿轮发生了故障。快速谱峭度方法得到的谱峭度图及平方包络谱,如图18所示。对比可知,本文所提方法对于齿轮调制频率及其倍频的特征提取能力和抑噪性能更强。

图13 磨齿齿轮信号的波形及频谱Fig.13 Waveform and spectrum of worn tooth gear
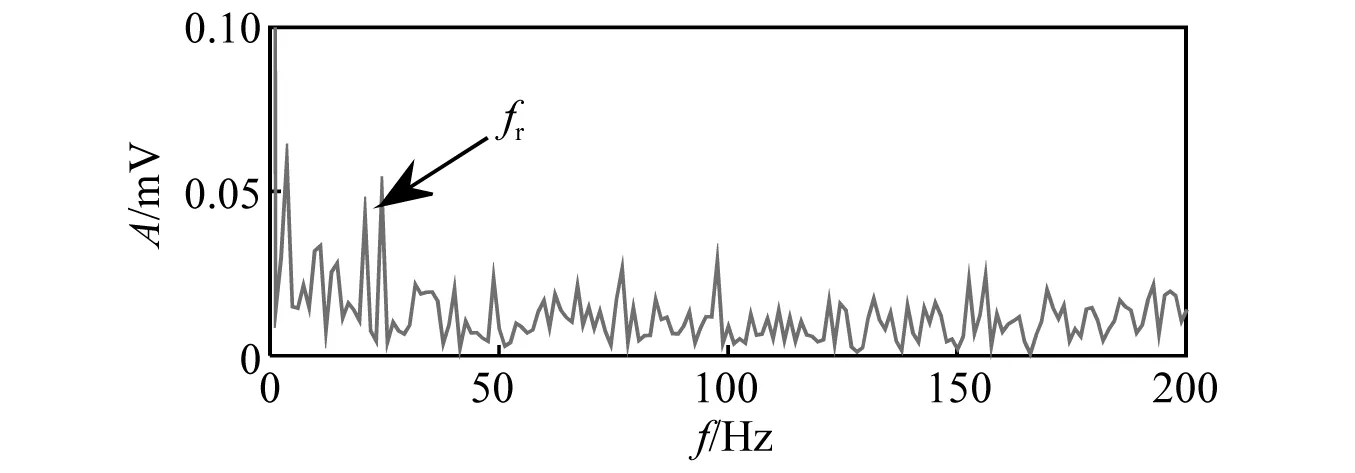
图14 磨齿齿轮信号的包络谱Fig.14 Envelope spectrum of worn tooth gear

图15 磨齿齿轮的SSWPT能量分布及边际谱Fig.15 SSWPT energy distribution and marginal spectrum of worn gear

图16 重构信号的波形及包络谱Fig.16 Waveform and envelope spectrum of reconstructed signal

图17 重构信号的波形及包络谱Fig.17 Waveform and envelope spectrum of reconstructed signal

表4 特征能量比Tab.4 Features energy ratio
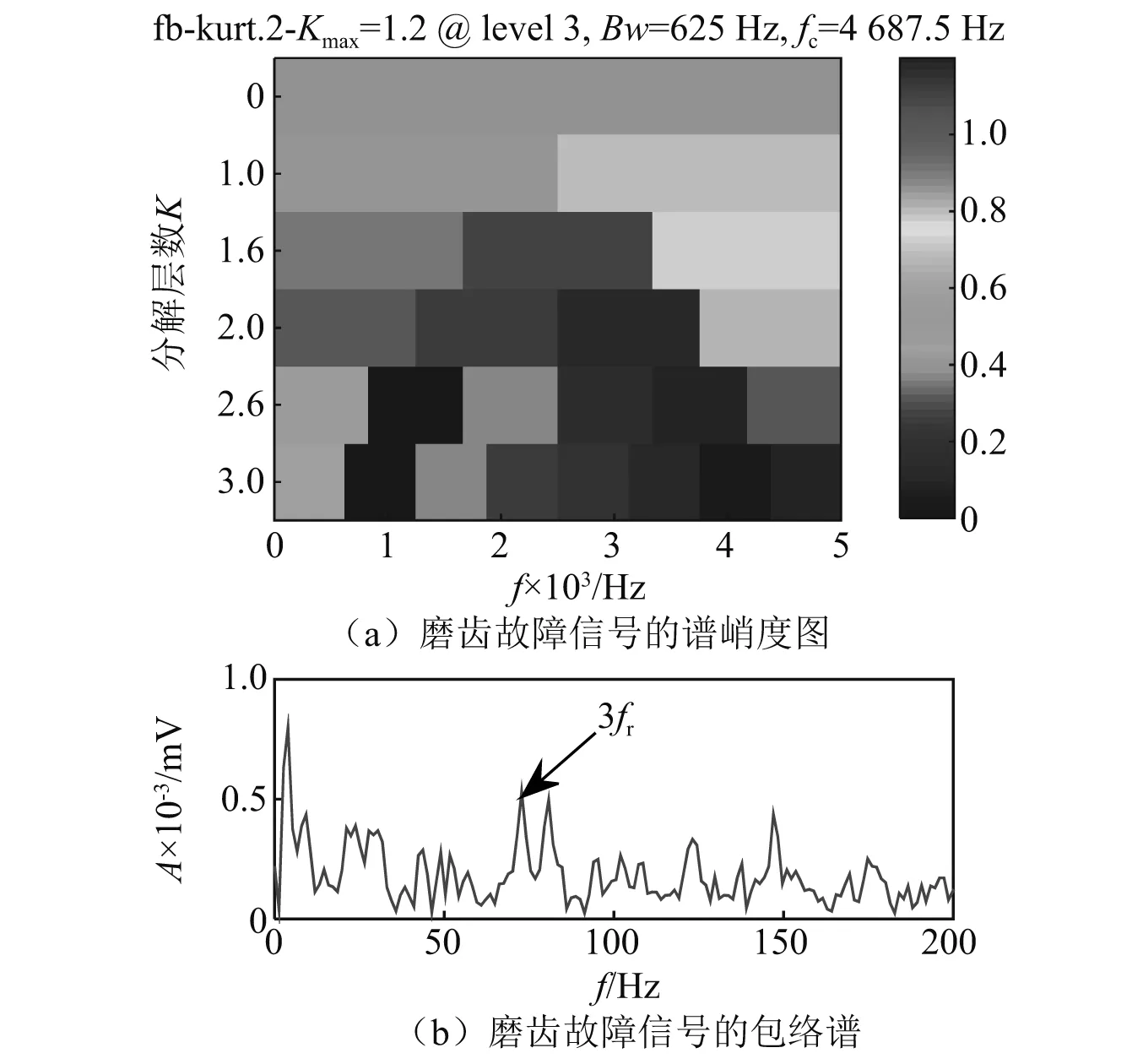
图18 磨齿故障信号的快速谱峭度分析Fig.18 Fast spectral kurtosis analysis of worn tooth fault signal
5 结 论
本文提出了基于SSWPT边际谱特征信息提取的齿轮故障诊断方法,通过仿真分析和对断齿、磨齿两种故障状态下的齿轮进行试验分析,结果表明:
(1) SSWPT边际谱具有特征增强的作用,能够有效的提取各阶啮合频率及其倍频,克服了传统分解方法存在的频率混叠,端点效应等问题。
(2) ISSWPT的重构效果比较理想,能够准确提取齿轮故障特征信息。
(3) 与包络谱和基于快速谱峭度的共振解调方法相比,本文提出的基于SSWPT边际谱方法在齿轮故障特征提取方面更有优势,其降噪和诊断效果更佳。
