多轴车辆线控液压转向系统设计及转角控制

2022-08-05石朝欢林贝清

中国机械工程 2022年14期

刘俊石朝欢林贝清黄鹤

1.合肥工业大学汽车与交通工程学院,合肥市，2300092.一汽解放柳州特种汽车有限公司, 柳州市，545000

0 引言

多轴转向车辆具有运动灵活、自由度多、通过性好等优点。目前多轴车辆的转向研究主要集中在以下几个方面：车辆的转向模式研究[1]；转向系统结构优化设计[2-3]；液压转向系统的研究[4]等。多轴车辆液压转向系统主要以全液压转向和液压助力转向为主，随着现代电子技术的发展，有学者提出了将线控转向和全液压转向技术相结合，开发了线控液压转向系统。线控液压转向系统由于抛弃了机械转向传动轴，通过电子控制单元(ECU)、传感器及阀控转向推力油缸对车辆实现线控转向，且可以根据车速及转向盘转角的变化对转向力实现柔性控制等优点，一般应用于产量较少的多轴导弹运输车或超多轴平板车(轴数多于8)等高端车型以及重型农业车上[5]。目前，国内商用车生产厂家为了降低研发及制造成本，针对一般性的多轴重型车辆多采用机械液压转向[6]，由于位于车辆后部的货厢部位的后转向轴与驾驶室的前转向轴距离较长，转向传动杆系刚度较小，随着车辆载货量的增加，杆系发生变形，后轴的转向轮转角误差不断加大，使得前后轴间转向不协调，导致后转向轴转向轮容易发生磨损。此外，在车辆高速行驶或在不平路面行驶时，较长的杆系容易发生摆振，也会导致后转向轴转向轮过多磨损。所以，迫切需要一种技术解决方案，能够在保留前转向轴机械液压转向系统前提下，减小货厢后转向轮的转向磨损。

本文研究的某型号8×2四轴重型车辆，位于驾驶室的双前桥(轴)为机械液压助力转向系统，第四轴不参与转向，为驱动轴,位于货厢部位的第三轴为转向轴。为控制成本，不改变轮胎转向磨损较小的一、二轴转向系统，在第三轴采用线控液压转向，解决第三轴转向轮由于转向不协调造成的磨损，使第三轴在转向时能以设定的角度跟随第一轴转向。目前，有关线控液压转向的研究多集中在低速重型农业车及其转向力、转向路感控制策略方面[7-8]，针对重型车辆线控液压转向系统及转角控制的研究鲜见报道。

本文首先设计了某型号8×2四轴重型车辆第三轴线控液压转向系统，并建立其动力学模型，然后设计了滑模闭环反馈控制器，对第三轴转向轮转角进行控制，最后通过仿真分析和实车试验验证了基于滑模控制器的转角控制的转向抗磨损性能以及效果。

1 线控液压转向系统

本研究设计的总体目标是开发出性价比高、性能稳定的后轴线控液压转向系统。该转向系统抛弃了前转向轴到后转向轴的转向纵拉杆，通过传感器从前第一转向轴获取转向信息，并完全依靠液压力推动后第三转向轴随前转向轴协调转向。

1.1 线控液压转向系统设计

为了实现第三轴的线控液压转向，利用传统的液压助力转向系统，在原有系统基础上装配电控单元、转角传感器、车速传感器和各种控制阀等。为防止第三轴轮胎在直线行驶时路面冲击导致转向轮偏转而造成轮胎磨损，执行机构采用对转向盘中位实现机械定位及自锁功能的对中自锁油缸，如图1所示。钢球在弹簧圈的作用下与活塞杆以及缸筒内壁紧密接触。当没有液压油输入油缸，活塞杆在其他外力作用下有移动趋势时，其运动方向侧钢球与活塞杆以及缸筒之间的压力加大，实现自锁；有液压油输入油缸时，油液推动可移动活塞，其凸缘推动逆移动方向侧钢球沿斜面下落实现解锁。

图1 对中自锁油缸结构图

图2所示为第三轴线控液压转向系统的总体设计。第一轴转角信号和车速信号被传感器采集后传至电控单元，电控单元经设定的控制算法得到第三轴车轮的目标转向角度，通过电液比例阀的电压信号，控制对中自锁油缸的活塞位移，进而控制第三轴车轮转动，与此同时利用转角传感器将第三轴车轮实际转角反馈给电控单元，构成闭环反馈控制跟踪第三轴目标转角，从而实现第三轴转向轮抗转向磨损的线控转向。

图2 线控液压转向系统的总体设计图

正常情况下，电磁阀3置左位，电磁阀4、5置右位，使冗余系统油路关闭，通过比例阀1和比例阀2控制对中自锁油缸实现转向。第三轴左转时，溢流阀按设定压力要求处于闭合状态，比例阀开始动作，此时阀1处于左位，阀2处于右位，油液由两端的A1、B2流入对中自锁油缸，由中间的A2、B1流出，油缸动作将第三轴转向横拉杆向右拉回，则车轮进行左转。右转同理。第三轴处于某个转角不动时，阀1、阀2处于中位截止状态，此时系统压力会迅速增大，当超过调定压力时，溢流阀开启，液压油从油箱经粗滤器、液压泵由溢流阀溢回油箱，对中自锁油缸处于自锁状态。当电控单元检测到故障时，比例阀1、2回到中位，该转向工作油路断开，冗余系统的三个电磁阀打开，阀3置右位，阀4及阀5置左位，使左缸油液由A2流入、B2流出，右缸油液由A1流入、B1流出，最终左缸活塞运动到左缸最左端面，右缸活塞运动到右缸最左端面，对中自锁油缸达到中位，从而第三轴转向轮对中，此时第三轴转向轮不跟随第一轴转向轮转向。由于活塞到达极限位置不再移动，此时油路压力增大，超过溢流阀的设定压力后，溢流阀开启，实现油压卸荷。

1.2 实车安装

为便于安装，根据总体设计图设计了液压集成阀块。集成阀块的结构如图3所示，其安装实例见图4a。将对中自锁油缸安装到车辆第三转向轴后方，其右端与车桥相连，左端通过连杆与转向横拉杆相连，如图4b所示，将4个油口分别与集成阀块的A1、B1、A2、B2相连。速度传感器安装在车辆变速箱输出轴上，转角传感器分别安装在第一轴和第三轴同侧转向主销顶端。

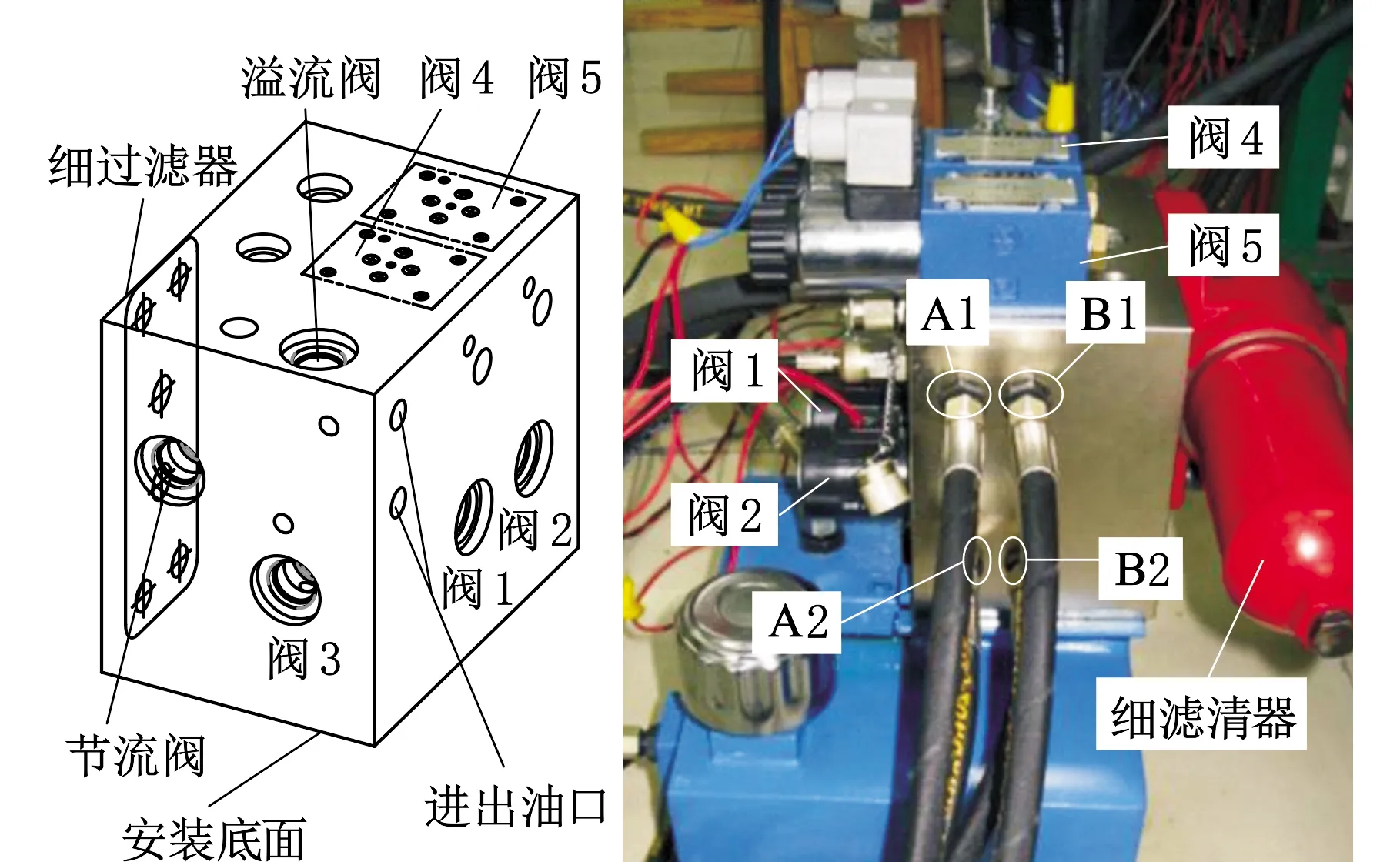
(a)集成阀块设计图 (b)集成阀块实物图

(a)集成阀块安装

2 线控液压转向系统动力学模型

2.1 电液比例阀系统模型

电液比例阀系统主要由电液比例阀(配套放大器)和对中自锁油缸(阀控缸)组成。

电液比例阀配置有位移反馈功能，根据其运动学特性可得出传递函数为

(1)

式中,x(s)为电液比例阀阀芯位移；U(s)为电液比例阀电压；KP为放大器增益系数；Kx为电液比例阀增益系数；ωh为电液比例阀固有频率；ξh为电液比例阀阻尼比。

以电液比例阀阀芯位移x(s)为输入量，对中自锁油缸位移y(s)为输出量，根据液压传动相关理论，可知其传递函数为

(2)

式中，ωn为液压系统固有频率；ξn为液压系统固有阻尼比；Ae为活塞有效面积；Kq为阀在稳定工作点附近的流量压力系数。

一般情况下ωn远小于ωh，因此电液比例阀和放大器可视为比例环节[9]，则电液比例阀系统的传递函数可写为

(3)

2.2 对中自锁油缸与车辆耦合模型

2.2.1多轴车辆转向二自由度非线性模型

对某8×2多轴重型车辆，建立其侧向、横摆二自由度转向动力学模型，其转向示意图见图5。

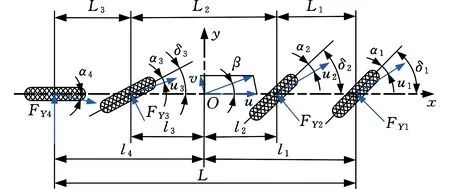
图5 某8×2多轴车辆二自由度模型

由牛顿-欧拉定理建立其侧向与横摆两自由度动力学模型：

(4)

式中，m为车辆质量；ωr为车辆横摆角速度；u、v分别为车辆质心速度在x方向和y方向的分量；l1、l2、l3、l4分别为第一、二、三、四轴到车辆质心的距离；FY1、FY2、FY3、FY4分别为第一、二、三、四轴轮胎的侧偏力；Iz为车辆绕z轴的转动惯量。

选择Pacejka轮胎模型[10-11]，有

FYi=D1sin(C1arctan[B1αi-E1(B1αi-arctanB1αi)])

(5)

(6)

i=1,2,3,4

式中，B1、D1、C1、E1为拟合系数，可由各轴车轮垂直载荷FZi、外倾角γ来确定[11]；β为车辆质心侧偏角；αi为各轴轮胎侧偏角，i=1,2时取“+”，i=3,4时取“-”；δi为各轴转向轮转角。

采用簧外瞬心法计算各轴车轮垂直载荷[12]：

(7)

(8)

(9)

式中，R0为外心距，R0>0则外心在第一轴外侧；Ki为各轴弹簧刚度；p为质心至第一轴的距离；pi为各轴至第一轴距离；G为车辆重力。

将式(5)、式(6)代入式(4)可得基于Pacejka轮胎模型的多轴车辆转向二自由度非线性模型。

2.2.2转向阻力矩模型

对中自锁油缸推动车轮转向需要克服相应的转向阻力矩。原地转向阻力矩主要为路面与轮胎间的摩擦力矩MR，而行驶中的转向阻力矩主要为回正力矩MA[13]。

原地转向阻力矩采用半经验公式计算：

(10)

式中，f为轮胎和路面间的滑动摩擦因数；pt为轮胎气压。

车辆正常行驶时的回正力矩主要包括重力回正力矩、由侧向力引起的自回正力矩、纵向力引起的纵向力回正力矩[14]。本文建立的多轴车辆二自由度模型不考虑左右轮负荷差别，故纵向力回正力矩忽略不计。

重力回正力矩

(11)

式中，Dr为主销偏移距；φ为主销内倾角。

自回正力矩由Pacejka轮胎模型得到：

MA2=D2sin(C2arctan[B2α3-E2(B2α3-arctanB2α3)])

(12)

式中，B2、D2、C2、E2为拟合系数，可由车轮垂直载荷FZ3、外倾角γ来确定[11]。

行驶中的转向阻力矩

MA=MA1+MA2

(13)

2.2.3对中自锁油缸与车辆耦合模型

设定液压转向系统油压ps为固定值，且回油压力为0，不存在任何泄漏情况，忽略液体的压力损失和压缩损失。对中自锁油缸推力

(14)

式中,S为对中自锁油缸截面积；D为对中自锁油缸内径。

不考虑机械运动副摩擦的能量损失，则对中自锁油缸推杆所做的功等于转向轮的转向阻力矩M所做的功，从而得到对中自锁油缸与第三轴转向轮基于能量的动力学耦合模型：

FLy=Mδ3

(15)

式中,y为对中自锁油缸位移。

原地转向时取M=MR，行驶转向时取M=MA。

由式(7)～式(9)及文献[12]可得式(5)拟合系数，联立式(3)～式(6)及式(10)～式(15)可得对中自锁油缸与车辆耦合模型。

3 第三轴轮胎转角控制

在8×2多轴重型车辆转向时，由第一轴转向轮的转角传感器获得实际转角信号δ1(t)，根据阿克曼转向原理计算出第三轴转向轮目标转角δ3d(t)，将第三轴转向轮目标转角与转角传感器反馈的第三轴转向轮实际转角δ3(t)进行比较，得出差值e(t)，经过滑模控制处理后输出电压控制信号U(t)，通过比例放大器放大后驱动电液比例阀工作，控制对中自锁油缸的位置，从而实现对第三轴转角的精确控制。基于滑模控制的多轴车辆线控液压转向系统转角控制逻辑如图6所示。

图6 控制逻辑框图

3.1 第三轴目标转角模型

第三轴转向轮在转向时纯滚动，其轮胎转向磨损最少，即第三轴和第一轴转向轮各转角间函数关系满足阿克曼转向原理。同轴转向轮转角的函数关系由转向梯形机构实现，同侧转向轮转角的关系由线控液压转向控制实现，故第三轴转向轮目标转角与第一轴转向轮转角的关系为

(16)

式中，L3为第三轴与第四轴轴距；L为整车轴距。

由式(16)可得第三轴转向轮目标转角关于第一轴转向轮转角的函数关系式：

(17)

为提高控制的实时性，建立离线数据表。第一轴转向轮向左最大转角 27°、向右最大转角 33°，设右转为正方向，则δ1∈[-27°,33°]，每0.1°取一个值，分别计算其对应的理论第三轴转角，储存在数组中作为离线数据表供调用，数据缺失项用所在区间端点数据平均值进行数据插补。如图7所示，δ1∈[-27°,33°]被分为600个区间，且δ3对应的区间长度在0.03°以内，故插值误差不超过0.015°。

图7 第三轴转角插值计算误差

3.2 滑模控制器的设计

线控液压转向系统存在诸多参数的不确定性，如车轮在转向过程中可能出现路面摩擦因数的变化、轮荷的变化、轮胎气压的变化、轮胎花纹的磨损等[15]。此外，其数学模型存在强非线性，普通线性控制器难以达到好的控制效果。滑模变结构系统最突出的优点是滑动模态对系统的干扰和参数摄动具有“完全自适应性”[16]，而且通过不连续的开关控制能够实现对非线性系统很好的控制效果，故滑模控制非常适用于线控液压转向控制。

在滑模控制器设计过程中，根据车辆非线性模型计算输出控制律时，由于模型复杂，导致计算繁琐，耗时过长。为了提高实时控制效果，基于理想的线性二自由度车辆行驶状态进行控制律输出的计算。

将FYi=kiαi代入式(4)得到整车线性二自由度模型：

(18)

式中，ki为各轴轮胎侧偏刚度。

将车辆行驶时的第三轴转向轮转向阻力矩简化为[17]

(19)

式中，ζ为轮胎总拖距；λ为加权系数。

代入理想的线性二自由度状态方程可得

M=Kδ3

(20)

联立式(3)、式(15)、式(20)可得

(21)

设目标转角为δ3d，则误差及其导数为

则切换函数为

(22)

其中，滑模面参数c1、c2均大于零。

采用指数趋近律：

(23)

其中，ε、k为大于零的控制系数，sgn(·)为符号函数。

定义Lyapunov函数为

(24)

对式(24)求导得：

S[-εsgn(S)-kS]≤-(ε|S|+kS2)≤0

(25)

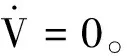
联立式(22)、式(23)，有

(26)

代入式(21)得其控制律为

(27)

根据比例切换控制方法，控制律取

(28)

其中，α、β为大于零的控制系数。

为了进一步削弱控制过程中控制输出量出现的抖振现象，可以用饱和函数sat(S)来代替不连续性函数sgn(S)[18]：

(29)

综上所述，滑模控制器的输出分别为

(30)

(31)

4 仿真与试验

4.1 仿真分析

比例切换及指数趋近律函数的控制系数由相同的优化算法获得[19]，且优化算法的参数设置基本相同。经优化后控制器参数如表1所示，车辆部分参数如表2所示。

表1 控制器部分参数

表2 车辆部分参数

为验证控制器的有效性，选取行驶时第一轴转向轮转角阶跃输入和正弦输入以及原地转向时第一轴转向轮转角阶跃输入三种工况进行仿真。三种工况下，基于阿克曼原理的开环控制、基于比例切换函数的滑模控制、基于指数趋近律的滑模控制的第三轴转向轮控制转角及基于阿克曼转向原理获得的第三轴转向轮目标转角曲线如图8～10所示。

图8 行驶时第三轴转角的角阶跃响应曲线

图8中，曲线a、b、c分别为20 km/h、40 km/h、80 km/h车速时的基于指数趋近律滑模控制下的第三轴转向轮控制转角，其余曲线为车速40 km/h时第三轴转向轮控制转角。当第一轴转向轮转角阶跃输入为30°时，第三轴转向轮转角目标值为6.9°，由图8可看出：开环控制时，曲线在1s左右到达目标值，随后出现约为1.2°的超调，至1.8s稳定，且到达稳态时的稳定值超出目标值0.9°，随着转向响应的滞后、超调和稳定值误差的增大，第三轴转向轮胎在转向过程中磨损也会更加严重；基于比例切换函数的滑模控制下0.6 s才第一次达到目标值，超调量达到0.3°，将近1 s后平稳，第三轴转向轮胎转向磨损有所改善；行驶车速为40 km/h时，基于指数趋近律的滑模控制不到0.8 s即达到稳定状态，且没有出现超调现象，较大程度地避免了第三轴转向轮胎的转向磨损，且此时转角曲线与行驶车速为20 km/h和80 km/h时的基本重合，稳定后差值在0.1°左右，达到了控制要求。在图9中，第一轴转向轮转角为正弦输入，正弦输入的振幅为30°、周期为3 s，车速为40 km/h。由图9可以看出：开环控制下的第三轴转向轮转角输出处于失控状态，达不到控制目标且车辆处于危险的状态；基于比例切换函数的滑模控制响应速度慢，与基于指数趋近律的滑模控制相比，其最大误差高于后者1.1°，跟踪性差。原地转向时，第一轴转向轮的角阶跃输入为30°，如图10所示：开环控制下的曲线出现了高频振荡，说明第三轴转向轮出现了摆振现象，第三轴转向轮胎转向磨损严重，这是由于原地转向时的转向阻力矩一般是行驶时的数倍，在控制时容易出现超调，进而导致转向轮摆振；基于比例切换函数的滑模控制出现了将近0.7°的超调量，且在0.6～1.6 s内出现低频率振荡，转向轮转向磨损较行驶时严重；基于指数趋近律的滑模控制出现了0.1°左右的超调量，对转向磨损影响较小。综上，基于趋近律的滑模控制不仅响应、趋近更加快速，而且曲线波动度小、超调持续时间短、稳态时差值小，能够较大程度上减少第三轴转向轮胎的转向磨损。

图9 行驶时第三轴转角的正弦响应曲线

图10 原地转向第三轴转角的角阶跃响应曲线

4.2 实车试验

为验证安装了基于指数趋近律滑模控制的线控液压转向系统在实车情况下的阿克曼转向转角控制效果和车辆的转向性能，对第三轴先后安装有线控液压转向系统及机械液压转向系统的四轴车辆进行原地转向及行驶转向试验。同时，针对多轴车辆的特点，根据汽车试验国家标准GB/T6323.2-1994及GB/T6323.6-1994，对第三轴先后安装有线控液压转向系统及机械液压转向系统的四轴车辆进行瞬态转向特性试验及稳态转向特性试验。

4.2.1原地转向控制

在原地操纵车辆转向系统进行原地转向测试试验。随机左右转动转向盘，记录下第一轴转角与对应的第三轴转角。现场试验如图11a所示。试验结果见图12，图中，黑色曲线表示第三轴的目标转角，红色曲线表示第三轴采用原机械液压转向系统时的转角，蓝色曲线表示第三轴安装了基于指数趋近律的滑模控制器的线控液压转向系统后的转角。

(a)原地转向

图12 原地随机转动试验

对图12进行分析可知，由于机械结构的变形及摆动，采用机械液压助力转向系统稳定后实验转角与目标转角误差最大将近2°，与目标转角均方误差为1.182°，偏差较大，这种情况下第三轴转向轮转向磨损严重，而采用线控液压转向系统稳定后第三轴转角与目标转角最大误差在0.7°以内，与目标转角均方误差为0.155°，接近于0，说明转向过程中误差很小，达到了较好的控制效果，可以大大改善第三轴转向轮原地转向时的磨损。

4.2.2行驶转向控制

使用配重模块模拟车辆的载重负荷，设定试验车速为20 km/h。车辆以试验车速稳定直线行驶后，急速转动转向盘至预先设定位置并固定数秒，记录下对应数据，现场试验如图11b所示。试验结果见图13，图中曲线含义同图12。

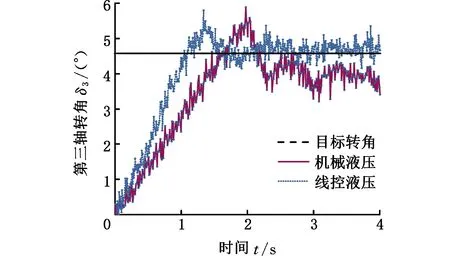
图13 行驶时第三轴转角的角阶跃响应曲线

由图13可知，线控液压转向系统角阶跃响应曲线1 s后第一次到达目标值，出现了约为0.6°的超调量，将近3 s时才达到稳定，对比图8，在精度上低于仿真试验且存在一定的滞后，原因主要是轮胎具有一定的刚度，液压系统存在阻尼、非线性特性以及控制系统的延时。机械液压助力转向系统角阶跃响应曲线1.7 s后第一次到达目标值，此后曲线存在小频率的波动(说明此时第三轴转向轮出现了摆振现象)且与目标转角相差1°左右，第三轴轮胎转向磨损严重。线控液压转向系统角阶跃响应试验转角与目标转角均方误差为2.004°，而机械液压助力转向系统角阶跃响应试验转角与目标转角均方误差为3.129°，前者响应过程符合度更高。以上分析说明线控液压转向系统转向精度更高、响应更快，行驶时第三轴转向轮转向磨损更小。

4.2.3稳态转向性能测试

采用60 m的直径圆周进行试验，车辆保持最低稳定车速沿圆周行驶后保持转向盘不动，缓慢连续均匀加速，直至车辆出现不稳定状态[20]。第三轴试验拟合测算的曲线如图14a、图14b所示。

试验时，侧向加速度随着车速的提高而变大，如图14a所示，车身侧倾角随着车速的提高而增大，由于试验车辆重心高、质量大，在试验中车身侧倾角超过4°时，车辆出现不稳定状态。如图14b所示，车辆的转弯半径比大于1，即转弯半径随车速提高而增大，表明车辆存在一定的不足转向特性，符合道路车辆行驶的安全性要求。由图14a、图14b中两条曲线基本重合可知，第三轴采用线控液压转向系统基本没有改变其转向稳态转向性能。

4.2.4瞬态转向性能测试

由于重型车辆高速转向具有失稳的危险性，故设定试验车速为20 km/h，车辆以试验车速稳定直线行驶后，保持油门开度不变，先按输入方向轻轻靠紧转向盘，消除转向盘自由行程，以尽量快的速度转动转向盘到预先位置并固定数秒[21]。试验结果如图14c、图14d所示。

(a)侧倾角拟合测算曲线 (b)转弯半径比拟合测算曲线

图14c、图14d中各曲线都能达到稳定但线控液压转向对应曲线波动较小，图14c、图14d中机械液压助力转向曲线分别滞后于线控液压转向曲线0.5 s、0.3 s左右，由行驶转向控制试验可知，第三轴采用线控液压转向系统后第三轴转角响应更快、精度更高且其曲线波动更小，故其侧向加速度以及横摆角速度响应略快于机械液压助力转向系统且波动更小,即第三轴采用线控液压转向系统的瞬态转向性能更好。

由以上分析可知，在实车上安装了基于指数趋近律滑模控制器的线控液压转向系统后，不仅其稳态转向性能基本没有改变、瞬态转向性能更优，而且使得第三轴转向轮转角响应更加迅速、控制误差更小、稳态差值更小，从而可以大大减少第三轴转向轮的转向磨损。