成形法双面磨削拓扑修形误差齿面对齿轮传动的影响

李 彦 汪中厚 刘 雷 刁鑫伟 王学军

1.上海理工大学机械工程学院,上海,2000932.南京航空航天大学机电学院，南京，210016

0 引言

齿轮磨削加工可以实现齿轮拓扑修形，对改善齿轮传动性能、提高承载能力、降低齿轮运行噪声具有重要作用[1]。许多学者对齿轮成形磨削与修形技术进行了研究。YOSHINO等[2-3]对附加单一运动的数控磨削方式进行研究，实现了直齿轮的双面磨削方法；夏政等[4]根据啮合原理对接触线与砂轮截形的求解进行研究，得出了斜齿轮全齿成形磨削砂轮的精确截形；汪中厚等[5]通过对实际成形齿轮磨削中的接触方程进行迭代求解得到了齿向修形齿面的误差模型；张虎[6]等基于Vericut平台，对斜齿轮成形磨削加工的整个过程进行仿真并对模型齿面进行了测量；LEE[7]、SHIH等[8-9]提出了齿面高阶多项式拓扑修形方法。在齿轮传动性能方面，文献[10-12]开展了相应研究，取得了一些有益成果。此外，陈思雨等[13]通过将齿轮副啮合刚度与静态传动误差引入到动力学分析模型中，研究了不同修形量与修形长度对直齿轮副齿轮动态性能的影响；朱才朝等[14]通过实验的方法研究了修形对风电齿轮箱传动性能的影响，表明合理的齿轮修形对减小齿轮传动啮合频率及其倍频处的振动加速度、振动烈度等要素都有明显作用；陈洪月等[15]以齿轮传动误差的波动与峰值为优化目标，采用遗传算法对齿面修形量与修形曲线进行优化；阳辉等[16]、汪中厚等[17]采用不同的方法对成形磨削斜齿轮进行了接触线优化，使斜齿轮磨削的齿向扭曲现象得到了改善。

本文首先建立了拓扑修形斜齿轮的螺旋面方程，根据啮合原理，推导了砂轮与斜齿轮齿面的接触条件式，进而得到砂轮轴向截形方程；然后，通过对砂轮截形方程进行推导，得到成形法双面磨削斜齿轮的原理性误差齿面数学模型并将误差曲面与理论齿面进行比对；接着，采用齿轮接触分析(TCA)方法获取斜齿轮副的传动误差和齿面接触斑点。实验研究表明：不同修形参数下的成形法双面磨削修形左齿面(双面磨削首先开始加工的齿面)与理论修形齿面相近，右齿面对比理论修形齿面在齿面误差、传动误差、接触区域方面存在较大差异，右齿面传动性能明显劣于左齿面，且不同轴交角磨削下的右齿面也存在较大差异。

1 成形法磨齿加工原理及数学模型

1.1 成形法磨削双面修形齿面加工原理

在磨削加工中，为了能精确控制砂轮与齿轮的相对运动以及联动，需要在齿轮上建立坐标系Sg(Xg,Yg,Zg)，并在砂轮上建立坐标系Sw(Xw,Yw,Zw)，如图1所示。其中,a为砂轮中心与齿轮中心间沿Xg轴方向上的最短距离；φ为Zg轴与Zw轴的交错角，即为砂轮安装角。

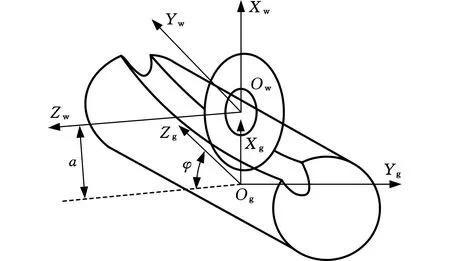
图1 成形磨齿法示意图

磨削时，砂轮回转面与齿轮待加工螺旋面将沿着一条曲线相切接触，这条曲线即为空间接触线。在加工过程中，通过改变砂轮截形实现齿廓修形，通过改变砂轮与齿轮中心距实现齿轮的齿向修形效果。

1.2 拓扑修形理论齿面方程

齿廓修形的目的是为了减小齿轮在啮入啮出期间的载荷波动，以及由此产生的啮入啮出冲击。齿向修形的目的是为了减少偏载现象的产生。齿廓修形的方式是将原来的渐开线齿廓在齿顶部位和靠近齿根部位的材料去除一部分。

将轮齿中间截面轴线与轮齿轴线交点作为直角坐标系Sg(Xg,Yg,Zg)原点，令Yg轴通过齿面节点P，Zg轴沿齿轮轴线方向，如图2所示。则未修形的齿面方程Σ1[18]可表示为

图2 齿面模型

r1(θ1)=(x1(θ1),y1(θ1),z1(θ1))

(1)

(2)

qs1(θ1)=q01+rb1θ1+S1(θ1)

(3)

q01=rb1tanαt

(4)

式中，S1(θ1)为齿廓修形曲线方程；θ1为渐开线发生线滚过的角度；p为螺距；αt为端面节圆压力角；rb1为基圆半径；b为齿轮宽度。

在齿廓方向上采用直线方式进行修形，齿顶修形量为e1，齿根修形量为e2，采用对应点渐开线发生线的滚动角θ代表修形长度。

如图3所示，修形曲线方程为

图3 齿廓修形

(5)

1.3 接触线法求砂轮截形

接触线是由齿轮螺旋齿面与该面共轭的砂轮表面之间的接触点构成的，在接触点处螺旋齿面的法线和砂轮的轴线必然相交。根据接触点齿面法线与砂轮轴线相交的特性，可以得到螺旋齿面与砂轮的所有接触点，接触点之间的连线即为接触线，接触线绕砂轮轴线回转可得到砂轮回转面，抑或接触线绕齿轮轴线做螺旋运动也可以得到齿轮齿形。

如图4所示，设接触点坐标为M(x1,y1,z1)，螺旋齿面在M点处的法线方程为

图4 砂轮接触方式

(6)

式中，x2、y2、z2为参变量；nx1、ny1、nz1为法线的方向分量。

由于M点不仅在法线上，还在砂轮轴线上，故砂轮轴线方程为

(7)

联立式(1)、式(6)、式(7)可得砂轮与齿轮的接触条件式[19]：

(a-x1+p*cotφ)nz1+any1cotφ+z1nx1=0

(8)

化简表示为

F0(u,θ)=0

(9)

将接触条件式与齿轮螺旋面方程联立，并转换到砂轮坐标系Sw(Xw,Yw,Zw)中，得接触点坐标：

(10)

由于砂轮截形为由y0=0平面截得的截线，所以最终砂轮截形方程为

(11)

其中，r0为中间变量。对上述方程采用牛顿迭代法进行求解，可以得到砂轮截形。

1.4 拓扑修形仿真齿面方程

齿向修形齿轮的附加运动会导致被磨削齿轮的齿形发生变化。为分析齿向修形齿轮产生的齿形变化，需计算齿向修形在不同轴向位置的齿轮实际齿形，并与理论齿形进行比较。

令齿轮齿面方程为

(12)

式中，R为砂轮半径线；γ为砂轮半径线R与OZwYw平面的夹角。

将其代入砂轮回转面方程式(11)中，可得[20]

(13)

砂轮回转面任一点的法向矢量n2为

(14)

磨齿过程中沿齿轮轴线方向改变齿轮与砂轮之间的中心距是最常用的修形方法[21]。设齿向鼓形修形中心距变动量为Δa，Δa可进行如下计算：

Δa(ξ)=δ(|ξ|-|Za|)cosβg/(bsinαn)

(15)

式中，βg为齿轮基圆螺旋角；b为齿轮修形齿宽;Za为修形起始点位置。

将式(8)砂轮回转面方程与接触条件式(13)联立，并将中心距变动量考虑在内，可得到双面成形磨齿轮螺旋面方程Σ2：

(16)

其中，R、γ、θ为参变量，R与γ需满足接触条件式。

2 拓扑修形齿面

2.1 接触线与砂轮截形计算

结合1.2和1.3节接触线方程和砂轮方程对表1所示的渐开线斜齿轮未修形时的砂轮截形进行计算。计算得到的接触线为三维空间曲线，将其投影到二维平面中，得到图5所示的接触曲线。再将空间接触线沿砂轮轴线进行旋转并投影，得到砂轮轴向投影如图6所示。

表1 斜齿轮参数

图5 接触线投影

图6 砂轮截形

2.2 不同修形量下的齿轮齿面

为研究不同修形情况下齿轮的传动性能，选择对50齿齿轮齿面进行拓扑修形，选取如下齿轮修形参数：齿廓修形方式选择折线修形，齿根部分修形起始位置压力角为19.9521°，修形终止位置压力角为15.9521°，齿顶部分修形起始位置压力角为23.9375°，终止位置压力角为27.9375°，齿向修形方式为鼓形修形，修形数据如表2所示，成形磨双面修形轴交角λ优化前为65.32°，优化后为64.89°，优化方式采用文献[17]中的神经网络方法，在此不作赘述。

表2 修形方式

对比标准齿轮，不同修形方式下的齿面误差数据如图7所示(各分图中左图为左齿面误差，右图为右齿面误差)。

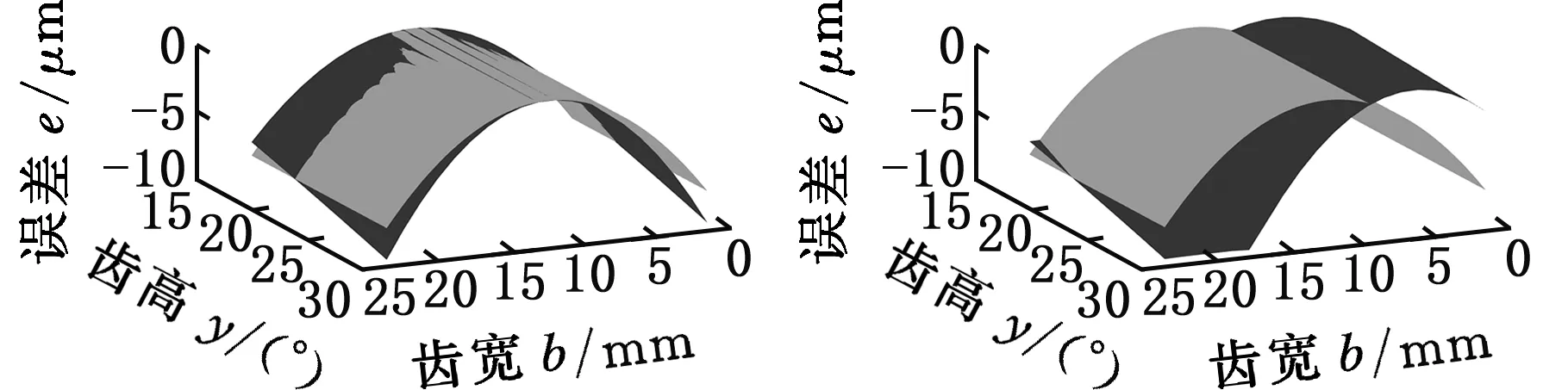
(a)λ=65.32°修形方式一时左、右齿面误差

观察图7a齿轮左齿面数据图可以发现，齿宽中部可以实现齿向鼓形修形，表明双面磨削方式的有效性，但在齿根部分出现微量欠修，齿顶部分过修，表现出了轻微的“齿形扭曲”现象。对比图7a、图7b 2组左齿面数据图可以发现，左齿面齿形扭曲对轴交角的变化不敏感，观察其余5组左齿面误差图可以发现同样规律。同样将图7a、图7b 2组右齿面数据图进行对比，可以发现两齿面存在较大误差，总体为齿向方向的鼓形峰值的偏移，即“齿向扭曲”现象[17]，出现此现象的原因是由于该齿轮为右旋齿轮，在成形磨双面磨削的过程中，左齿面先与砂轮发生接触，产生磨削效果，右齿面由于后接触，会导致无法避免的齿向扭曲现象，并且同样对比图7c～图7f 2组数据可以发现，在轴交角为65.3232°时，齿向扭曲现象更为明显，在进行轴交角优化后，齿向扭曲现象明显减弱。

3 拓扑修形斜齿轮传动接触分析

3.1 齿面接触分析模型

文献[12,20]对齿面接触分析技术进行了诸多研究。对1.1和1.4节中计算得到的主动齿轮齿面方程Σ1和从动齿轮齿面方程Σ2进行坐标转换，两齿面在同一坐标系下的位置矢量rf和法向矢量nf分别为

(17)

式中，Mf1、Lf1、Mf2、Lf2为从齿面坐标系到固定坐标系的转换矩阵；u1、θ1、u2、θ2为齿轮的齿面参数；φ2、φ1为齿轮的运动参数。

由于两接触齿面始终处于连续相切接触，如图8所示，两接触点的位置矢量与法线矢量在任一瞬间都重合，因此得到

图8 齿面接触示意图

(18)

曲面的单位法线矢量可以表示为

(19)

由此得到含有6个未知量u1、θ1、φ1、u2、θ2和φ2的方程，给定其中的φ1，得到

f(u1，θ1,u2,θ2,φ2)=0

(20)

由于齿轮在啮入啮出时会发生齿轮齿面边缘与另一齿轮齿面发生接触的情况，即边缘接触，故边缘接触条件为

(21)

采用Newton-Raphson方法对式(20)、式(21)进行求解，确定每个瞬时接触点的位置，进而获得齿轮接触印痕与传动误差。传动误差表现为随主动轮变化的被动齿轮实际转角与理论转角的差值，其关系为

s=rb1[φ2(φ1)-(Z1/Z2)φ1]

(22)

3.2 双面磨削拓扑修形对传动误差影响

表1所示的齿轮副主动轮为39齿齿轮，采用3.1节建立的接触分析模型进行求解，得到的传动误差数据如图9所示。

(a)双面磨削修形左齿面接触传动误差

理论修形齿面的左右齿面相同，因此传动误差数据也完全一致。

如图9a、图9c左齿面接触传动误差所示，在修形方式一时传动误差峰峰值达到最小，并且相较于未修形齿面传动误差明显减小。如图9a所示，不同修形方式下的左齿面接触的传动误差相位基本一致，不同轴交角磨削生成的左齿面对传动误差影响较小，明显小于修形方式发生改变时的传动误差变化。如图9b所示，不同轴交角下右齿面接触的传动误差较左齿面发生了明显的相位差，传动情况发生了较大差异，后续进行详细分析。

图10所示为修形方式一传动误差,其具体数据如表3所示。

图10 修形方式一传动误差

表3 修形方式一传动误差

由表3可知，成形磨双面修形中，与理论修形齿面相较,左齿面传动误差峰峰值和均值均有上升，轻微的齿形扭曲对传动误差有一定影响；两不同轴交角下的左齿面传动误差峰峰值与理论齿面传动误差峰峰值之间的差值分别为0.13 μm和0.16 μm，二者相差约8.57%，表明不同轴交角对左齿面传动性能影响较小。反观右齿面，由于齿向扭曲现象的存在，导致右齿面接触传动过程中的齿轮副传动误差有较大改变，不同轴交角对应的右齿面接触传动误差亦有较大的差别，65.32°轴交角时的右齿面传动误差峰峰值相较64.89°时有显著提高，两轴交角下与理论齿面传动误差峰峰值之间的差值分别为1.29 μm和0.33 μm；右齿面传动误差曲线较理论修形齿面也存在明显的相位差，相位差从轴交角为65.32°时的3.15°减小到轴交角为64.89°时的2.03°，减小了约55.17%。

表4、表5所示分别为修形方式二、修形方式三下的传动误差，可知，在添加了齿廓修形后，随齿廓修形量的增大，左齿面接触传动误差与理论修形齿面接触的传动误差差值愈发减小，其相对误差从轴交角64.89°下修形方式一时的0.16 μm减小到方式三时的0.03 μm，降幅约81.3%；右齿面接触的传动误差峰峰值依旧高于左齿面，但左右齿面差异幅度减小，从轴交角64.89°下修形方式一的32.69%减小到方式三时的15.04%；随着齿形修形量的增大，相位角偏差也相应降低，从修形方式一时的2.03°减小为修形方式三时的0.45°,降幅约为77.8%。

表4 修形方式二传动误差

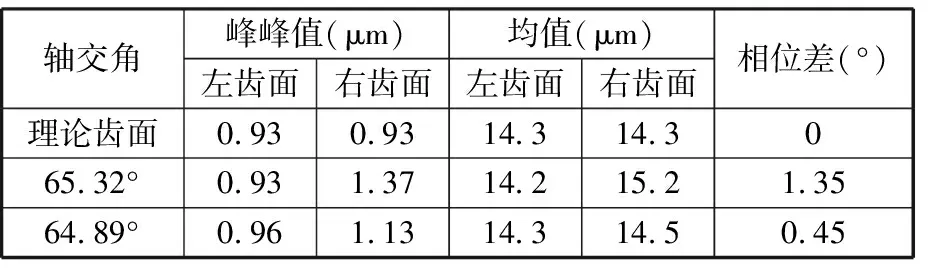
表5 修形方式三传动误差

由表3、表4、表5可知，成形双面磨修形左齿面可以基本实现理论齿面拓扑修形效果，齿形扭曲对左齿面传动性能影响较小；但对于右齿面而言，由于齿向扭曲现象存在，导致右齿面传动性能明显劣于左齿面，并且传动中存在一定的相位差。不同轴交角双面磨削下的传动误差也有较大差别，合适的轴交角可以使右齿面明显减轻齿向扭曲现象，使传动误差显著减小。

3.3 齿面接触分析

将齿面接触分析结果进行插值拟合，得到齿面接触结果如图11所示。

如图11a～图11d所示，在理论修形的情况下，左右齿面接触传动的接触情况基本相同，随着修形量的增大，接触区域形状发生了明显改变。对比图11b/图11e/图11f、图11c/图11g/图11h与图11d/图11i/图11j可以发现，双面磨左齿面接触传动时的齿面接触情况与理论齿面基本相同，表明轻微的齿形扭曲对齿面接触形状影响较小，不同轴交角下的左齿面接触形状也基本一致。对比右齿面接触传动，理论修形与不同轴交角时的齿面接触情况都有明显不同，右齿面传动时齿面发生了明显的偏载现象，轴交角为65.32°时的齿面偏载情况最为严重，这与右齿面误差图的结果是相对应的。

(a)标准齿轮左、右齿面

综上分析可知，成形双面磨削修形左齿面接触情况与理论修形齿面类似，齿形扭曲造成的影响可基本忽略；右齿面接触情况较理论修形齿面有较大差别，齿面发生了明显的偏载现象，改变轴交角可以使偏载状况发生明显改变。

4 实验验证

4.1 齿轮磨削测量实验

为验证本文研究结果的可靠性，在L300G全数控齿轮磨削中心上进行齿轮双面磨削修形实验，齿轮参数同前述仿真参数，修形参数采用修形方式二的参数，轴交角为65.32°和64.89°，并置加工后的齿轮于Gleason 350GMS齿轮测量中心上进行齿面测量，如图12所示。

(a)L300G全数控齿轮磨削中心 (b)加工过程

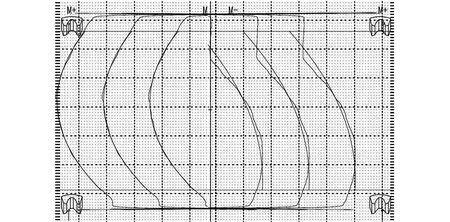
(a)65.32°齿向测量结果

齿面测量结果如图13所示，可知，右齿面发生了明显的扭曲，与数值仿真结果趋势基本一致，验证了该齿面计算方法的有效性。

(d)64.89°齿形测量结果

4.2 齿轮传动实验

对上述齿轮左右齿面进行传动实验，实验结果如图14所示。右齿面相较于左齿面的接触区域明显发生偏移，验证了本文仿真结果的正确性。

(a)65.32°左齿面传动 (b)65.32°右齿面传动

5 结论

(1)基于斜齿轮成形磨齿加工工艺，实现了建立斜齿轮齿廓方程、求解接触线方程、计算砂轮截形、完成斜齿轮成形磨削数值仿真齿面一系列流程，得到了基于斜齿轮成形双面磨削拓扑修形的齿面误差模型，结果表明，左齿面相较理论齿面存在轻微齿形扭曲，右齿面存在明显齿向扭曲现象。

(2)完成了理论修形齿面和成形双面磨削左、右修形齿面接触情况下的传动误差分析，通过分析可知：左齿面齿形扭曲对齿轮传动性能影响较小，左齿面可基本实现理论修形效果；右齿面齿向扭曲显著影响了齿轮的传动误差，右齿面性能明显劣于左齿面；合适的修形方式与轴交角可以明显减轻右齿面齿向扭曲现象，传动误差明显减小，使左右齿面传动误差差异缩小在15%左右。

(3)完成了理论修形齿面和成形双面磨削左、右修形齿面接触情况下的齿面接触斑点对比，分析对比结果可知：齿形扭曲对左齿面接触斑点影响较小；齿向扭曲对右齿面影响显著，右齿面发生了明显的偏载现象，合适的轴交角可以有效减少齿面偏载现象。