双支链六自由度并联机构尺度设计与性能分析
2022-08-05谢志江范乃吉吴小勇
谢志江 程 清 丁 军 何 苗 范乃吉 吴小勇
1.重庆大学机械传动国家重点实验室,重庆,4000442.重庆理工大学机械工程学院,重庆,4000543.中国工程物理研究院激光聚变研究中心,绵阳,621900
0 引言
并联机构因其刚度高、承载能力强、累积误差小、动力性能好等优点而得到广泛应用[1-2]。自Stewart平台提出以来[3],已有许多学者对六自由度并联机构进行了广泛的研究。MCCANN等[4]基于Stewart平台开发了一种能精确完成抓取任务的新型灵巧手。AGINAGA等[5]利用逆奇异性对6-RUS并联机构的刚度进行了分析,并由此获得了一种提高机构沿路径方向刚度的方法。HE等[6]将六足爬壁机器人视为6-SRRR并联机构,基于结构约束方程和雅可比矩阵对机器人的工作空间及奇异性等运动学性能进行了研究。FENG等[7]提出了一种宏微双驱动并联机构用于染色体切割,其宏动部分采用6-PPPS机构,微动部分为6-PSS机构,并对该并联机构的运动学、各向同性等进行了分析。上述机构都具有六条运动支链,支链数目较多,使得干涉增加进而会缩小机构的工作空间。相对而言,支链数目的减少有利于扩展机构工作空间,可以有效应用于康复机构、风洞试验、航空航天等领域中,因而少支链并联机构已逐渐成为并联机构的研究热点之一[8-9]。
近年来,国内外许多学者提出了多种三支链六自由度并联机构。郭宗和等[9-10]对3-PRRS及3-PRPS并联机构的位置正逆解进行了分析。冯祥文等[11]提出了一种3-URS并联机构,并对其姿态工作空间进行了研究。NAG等[12]设计了一款3-RPRS并联机构,该机构每条运动支链有两个驱动关节,并基于闭环矢量法求解了该机构的位置正解。CHABLAT等[13]提出了一种3-PPPS并联机构,并对该机构的奇异性进行了研究。COPPOLA等[14]提出了一种六自由度可重构并联机构,分析了该机构的运动学、刚度等性能,并对该机构进行了多目标优化设计。
上述六自由度并联机构都包含三条及以上运动支链,而两支链六自由度并联机构则鲜有研究。鉴于此,本文提出了一种新型六自由度并联机构,该机构由两条运动支链组成,每条支链各包含一个主动球副。首先基于封闭矢量法求得机构运动学位置逆解,揭示机构输入与输出的速度映射关系,得到该机构的雅可比矩阵。其次,借助性能图谱法完成了机构尺度设计。最后对该机构在特定工作姿态下的工作空间、灵巧度、承载性能及刚度性能进行了全面研究和综合评价。
1 机构简介


图1 人体双臂结构
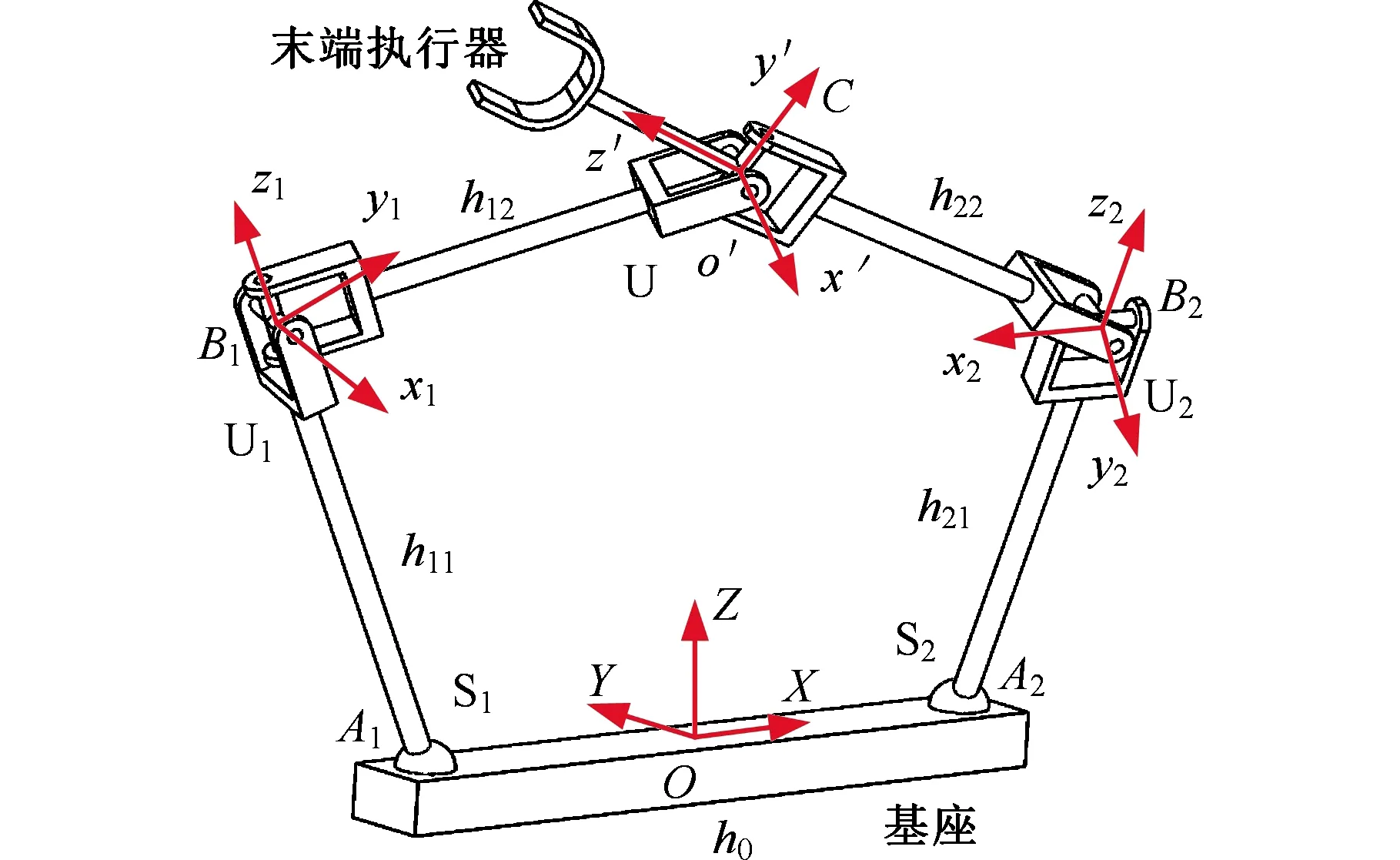
图2 并联机构运动简图
根据该机构特点建立定坐标系OXYZ,其坐标原点O位于两主动球副中心连线A1A2的中点,X轴平行于A1A2指向球副S2,Z轴垂直于水平面向上,Y轴满足右手定则。在末端执行器上建立动坐标系o′x′y′z′,其坐标原点o′与虎克铰U的中心点C重合,x′轴与虎克铰U在第一条支链的旋转轴重合,y′轴与虎克铰U在第二条支链的旋转轴重合,z′轴满足右手定则。主动球副坐标系与驱动连杆坐标系方位相同,为方便描述,在驱动连杆AiBi末端建立局部坐标系Bixiyizi,其坐标原点Bi与虎克铰Ui的中心重合,xi轴与虎克铰Ui在AiBi的旋转轴重合,zi轴平行于AiBi,yi轴满足右手定则。
根据Grübler-Kutzbach公式可计算该机构自由度为
(1)
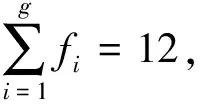
2 位置逆解与雅可比矩阵
2.1 机构位置逆解
位置逆解分析就是已知末端执行器位姿,求解主动球副的输入旋转角度,建立两者的映射关系。已知动坐标系o′x′y′z′原点相对于定坐标系OXYZ的位置向量为P=(x,y,z)T,绕X、Y、Z轴旋转的角度分别为α、β、γ,则末端执行器的旋转矩阵R可表示为
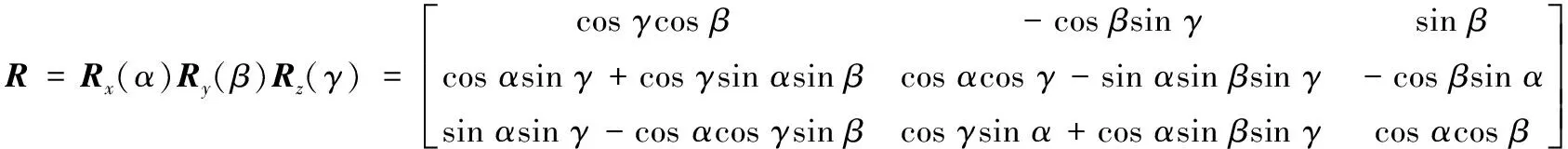
(2)
式中,Rx、Ry、Rz分别为末端执行器绕X、Y、Z轴的旋转矩阵。
如图3所示,该机构可分为两条运动支链,gi1、gi2分别为沿AiBi、CBi方向的单位向量,fij、θij(j=1,2,3)分别为与虎克铰转动轴线平行的单位向量及对应的转动角度。沿支链从定坐标系到动坐标系可形成两矢量闭环(图4),取任一支链建立封闭矢量方程:
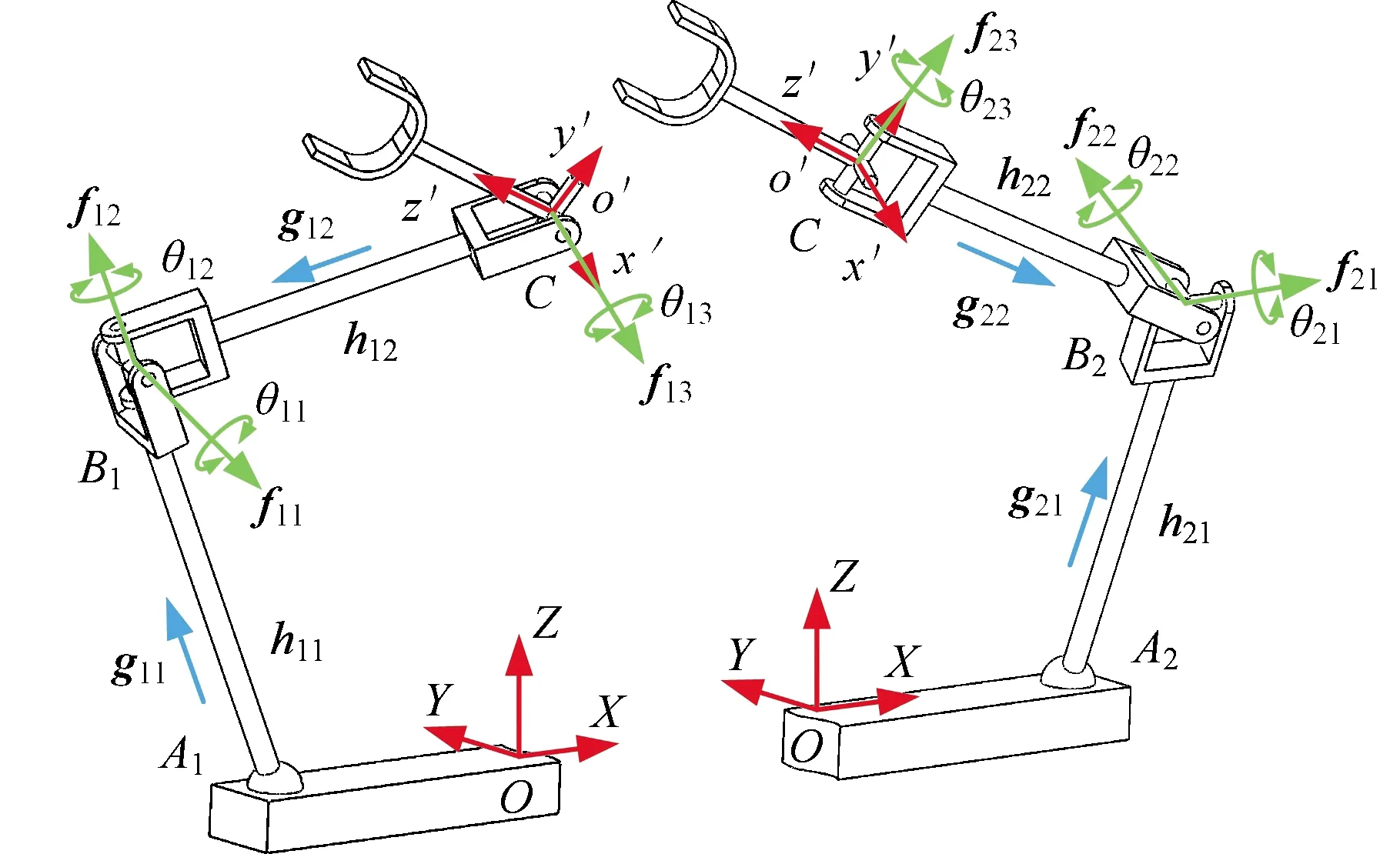
图3 各支链机构简图
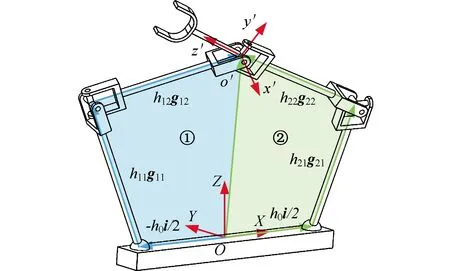
图4 支链矢量闭环
hi1gi1=P+hi2gi2-(-1)ih0i/2
(3)
g12=RRx(θ13)kg22=RRx(θ23)k
式中,i、k分别为X、Z轴单位方向向量。
已知杆AiBi的长度为hi1,即‖P+hi2gi2-(-1)ih0i/2‖=hi1,可得
Misinθi3+Nicosθi3+Qi=0
(4)
Mi=-2hi2[zcosγsinα+(h0/2-x)cosβ-
ysinαsinβsinγ+cosα(ycosγ+zsinβsinγ)]
Ni=2hi2[zcosαcosβ-ysinαcosβ+
(x-h0/2)sinβ]
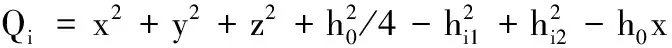
对式(4)进行求解,可得
(5)
由此,局部坐标系Bixiyizi的单位方向向量可以表示为
(6)
f12=RRx(-θi3)jf22=RRx(θi3)i
式中,a、b、c分别为对应向量的第一个元素、第二个元素和第三个元素;j为Y轴单位方向向量。
可以求得
(7)
式中,αi、βi、γi为主动球副Ai的三个姿态角。
即可求得机构的位置逆解。
式(5)和式(6)中,由于“+/-”号的取值不同,在确定末端位姿后,由θi3(‖AiC‖≠hi1+hi2)及xi可分别求得两组解,因此每条支链存在四种可能的位置,如图5所示。将四种位置构型分别定义为⊕⊕、⊕⊖、⊖⊕以及⊖⊖,每组中的两个符号分别代表θi3和xi的“+/-”号取值。综上可知,确定一个末端位姿后,该机构具有4×4=16种可能的工作模式,如表1所示。为方便计算分析,后文均采用1号工作模式。
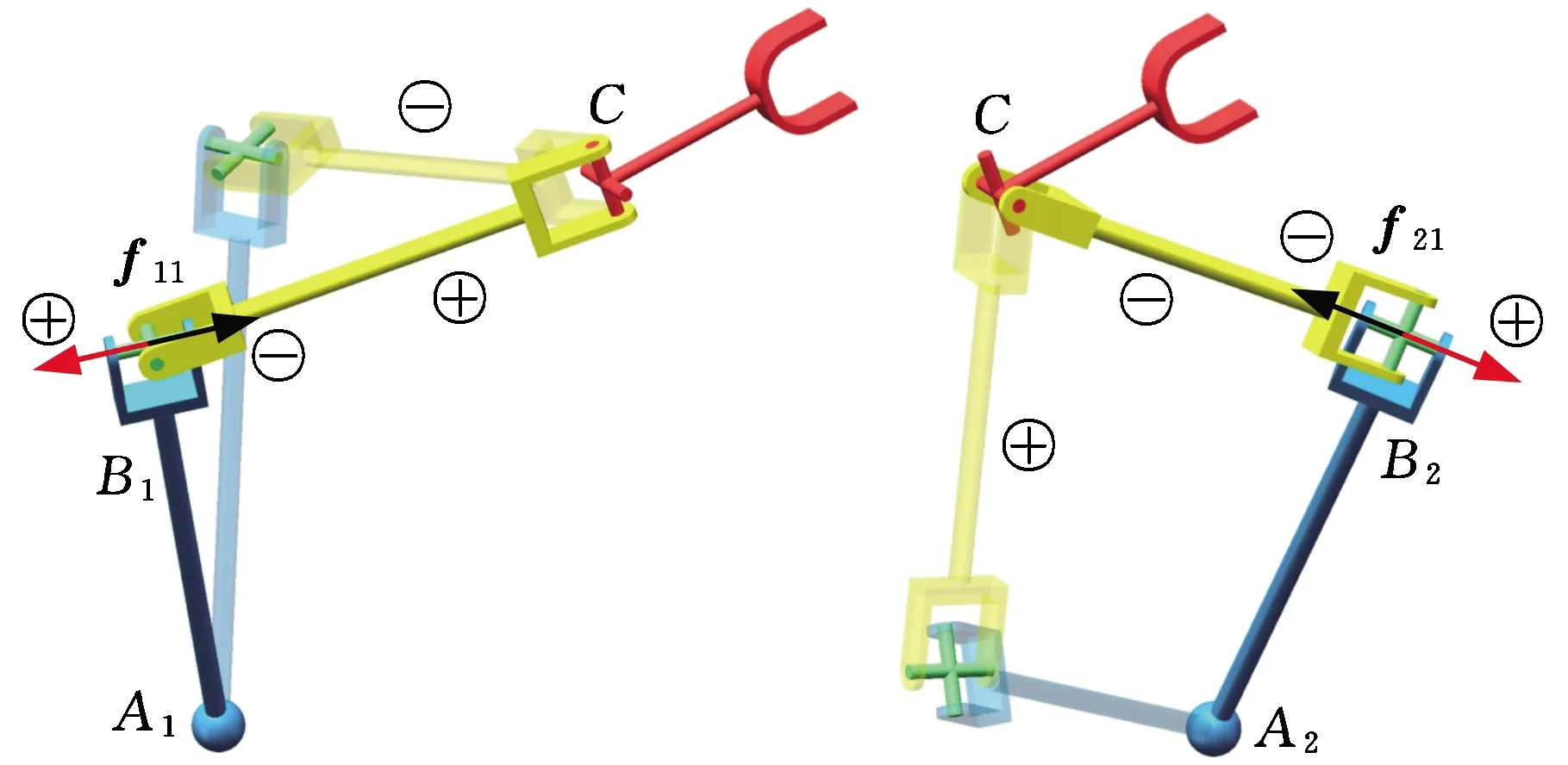
图5 各支链可能的位置构型
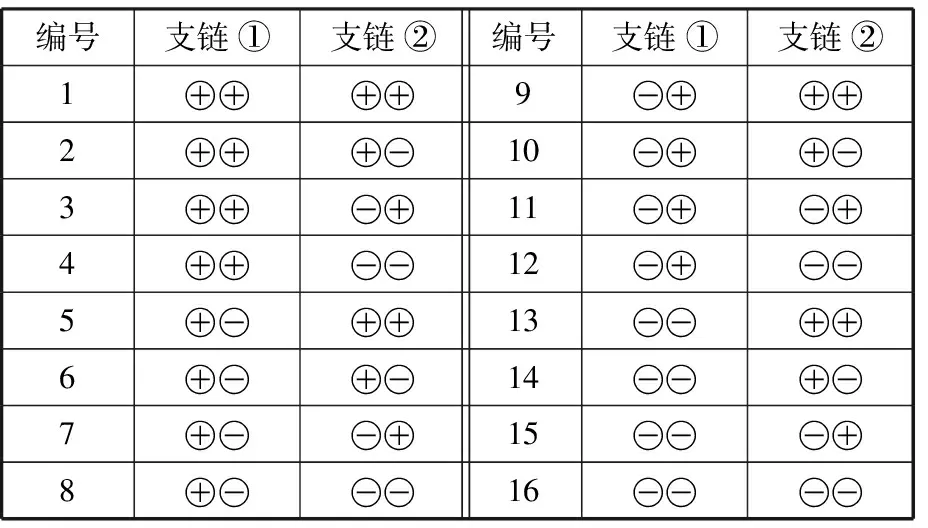
表1 机构的16种工作模式
2.2 位置逆解仿真
为验证运动学分析的正确性同时对运动效果进行说明,本文采用MATLAB进行理论计算,并通过ADAMS进行仿真验证。此处,机构末端姿态固定(α=0°,β=-45°,γ=-90°),位置输入为
(8)
MATLAB数值计算与ADAMS仿真计算的结果如图6所示。对比可知,数值计算与仿真计算的结果基本一致,由此验证了位置逆解的正确性。
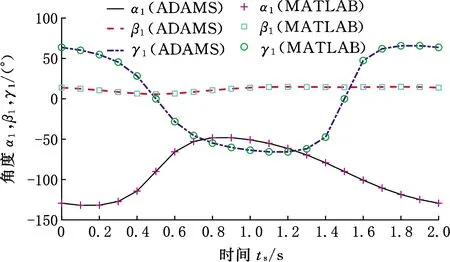
(a)支链1仿真计算结果
2.3 雅可比矩阵求解
根据前文,将式(3)等号两边分别对时间求导可得
(9)
ωi=(ωix,ωiy,ωiz)
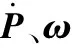
对式(9)等号两边分别点乘gi2、fi2、fi3可得
(10)
(11)
(12)
末端执行器的角速度向量ω需满足
(13)
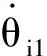
(14)
将式(14)代入式(11)可得
(15)
将两条支链的参数分别代入式(11)、式(12)、式(15)并联立写为矩阵形式:
(16)
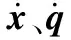
当矩阵Jq为非奇异矩阵时,可得到两球副的驱动速度与末端执行器速度之间的映射关系为
(17)
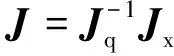
3 性能评价指标
3.1 可达工作空间性能指标
并联机构的可达工作空间一般较小,且由于多支链、多关节相互约束的复杂性,无法直观地得到确切的解析解,因此本文采用全局搜索法研究该机构的可达工作空间,具体步骤如下:
(1)设置x、y、z、α、β、γ六个位姿参数的搜索范围,各参数的搜索范围应略大于结构参数的极限以确保计算结果能够囊括可达工作空间中所有的点。
(2)设置一定的步长,将步骤(1)设定的搜索范围离散化,并将离散化后的点作为末端执行器的位姿参数,解算出每个离散点的位置逆解,得到两驱动关节的姿态角及三个虎克铰对应的旋转角。
(3)检查机构各关节是否满足约束条件,若满足,则判定该点位于机构的可达工作空间内,所有可行点即构成了机构的可达工作空间。
以可达工作空间为基础,定义机构工作空间性能指标[15]为
(18)
其中,nws为符合约束条件的可达工作空间的离散点数,nd为搜索范围离散化后的所有点数。将工作空间大小比值N作为机构工作空间大小的评价指标。
3.2 灵巧度性能指标
灵巧度描述了机构输入与输出之间的传递关系,常用于评价机构的运动精度。通常机构的灵巧度可通过局部条件数(local conditioning index, LCI)来衡量机构在特定形位下的局部灵巧度[16-17],其表达式为
(19)
kc=‖J‖‖J-1‖
其中,kc为雅可比矩阵的条件数。LCI值VLCI的取值范围在0~1之间,当VLCI=0时,机构处于奇异位形,灵巧度最差;当VLCI=1时,机构各向同性,灵巧度最好。LCI用于描述确定尺度参数后机构灵巧度的分布情况,为衡量机构在工作空间全域下的灵巧度,引入了全局条件数(global conditioning index, GCI),其表达式为
(20)
3.3 承载能力性能指标
承载能力决定了机构的工作负荷能力,是评价机构性能的重要指标。根据虚功原理,作用在机构末端执行器上的广义力F与其驱动力f之间有如下关系[18]:
F=JTf
(21)
该机构的承载能力指标定义为‖f‖=1时输出力矢量F的模的极值。为求得该极值,构造如下拉格朗日方程:
LF=fTJJTf-λF(fTf-1)
(22)
式中,λF为拉格朗日乘子。
当‖f‖=1时,承载能力极值为JJT的最大、最小特征值的开方,即
(23)
式中,λFmax(JJT)、λFmin(JJT)分别为矩阵JJT的最大、最小特征值。
本文取最小承载能力极值‖Fmin‖用于评价机构在给定位姿下的承载能力,‖Fmin‖越大,表明机构的承载能力越好。
3.4 刚度性能指标
当末端执行器作用于物体时,作用反力将引起末端偏离理想位置,其偏离的大小与其作用力和机械手的刚度有关。在笛卡儿空间内机构的局部刚度矩阵可表示为
KL=JTKJJ
(24)
KJ=diag(k1,k2,…,kg)
式中,KJ为机构的关节刚度矩阵;ki(i=1,2,…,g)为每个驱动关节的关节刚度。
假设每个驱动关节都有相同的刚度k,则式(24)可简化为
KL=kJTJ
(25)
对应的KL主对角线上的元素可以作为机构在各方向上的局部刚度指标(local stiffness index, LSI)[19]。
4 机构尺度设计
尺寸参数对机构各运动关节的布局及机构的工作性能有着非常重要的影响,其确立过程大多需考虑机构的关节约束、几何尺寸约束、动态性能等条件。在机构的设计阶段,性能指标是对机构性能进行量化的依据,因而性能评估对机构的设计有着指导性的作用[20]。在工程实际应用中,同时考虑所有性能指标进行尺度设计是一项比较困难的工作。本文所设计的机构在具备较大工作空间的同时也应拥有良好的灵巧度,为此上述两项性能指标将作为尺度设计的依据。
相比基于目标函数的优化设计方法,性能图谱法的优化结果更加灵活,对于特定的优化设计任务,该方法可以得到不止一个优化结果,设计人员可以根据设计条件灵活地对优化结果进行调整[20]。
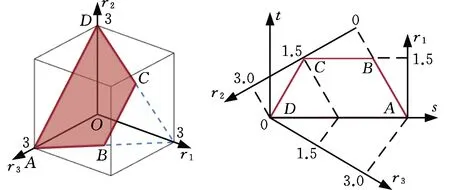
根据该机构特点,选取连杆长度h0/2、h11、h12、h21、h22作为尺寸优化参数,本文主要考虑机构处于对称的情形,即h0/2=d1、h11=h21=d2、h12=h22=d3。为便于机构尺度设计,需要消除机构尺寸参数的物理属性,将物理参数d1、d2、d3转换为量纲一参数变量r1、r2、r3[21-22],即
(26)
其中,归一化因数D=(d1+d2+d3)/3,为保障该机构能够成功装配,量纲一尺寸参数r1、r2、r3应满足:
(27)
根据式(26)和式(27),可将三维设计空间转换为等效的二维平面空间,其转换关系为
(28)
其中,s、t分别为二维空间的横纵坐标,如图7所示。
(a)三维设计空间 (b)二维设计空间
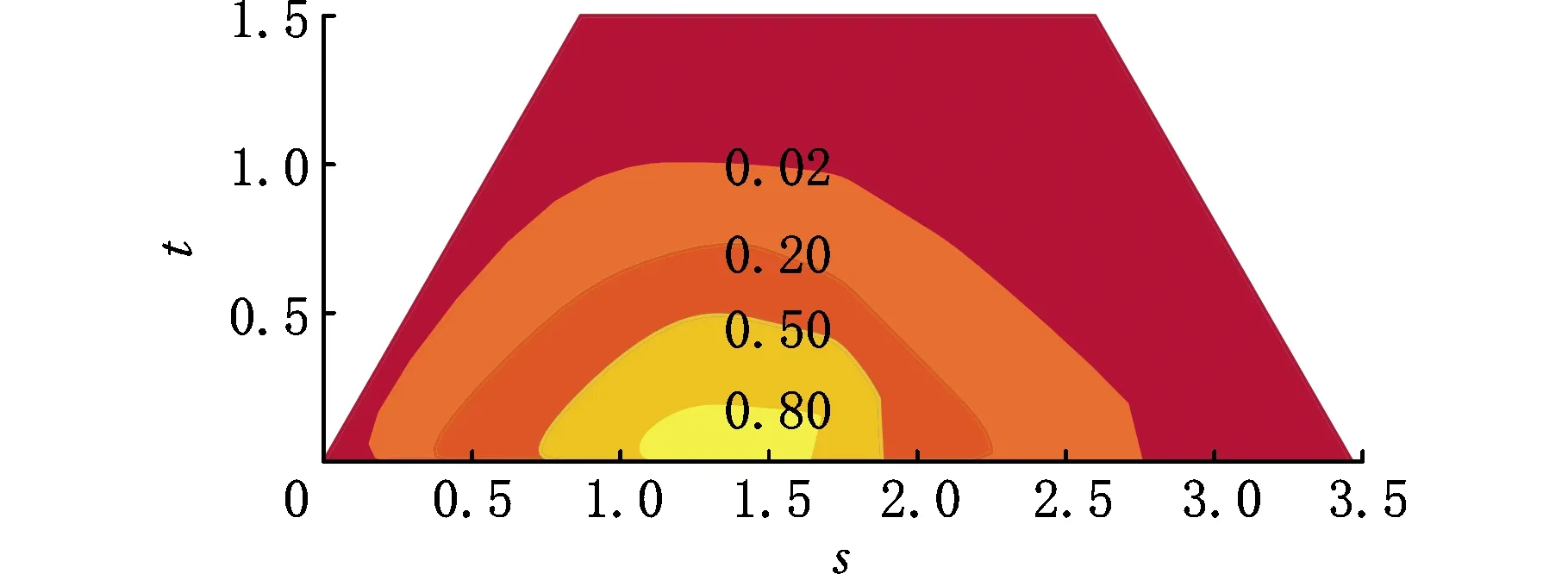
机构工作空间与GCI性能图谱分别见图8a和图8b,可以看出,r1越小,工作空间性能指标N值越大,GCI值VGCI越小。考虑到机构在实际的工程应用中所计算出的数值最优解并不一定能满足设计要求[20],故综合选取优化目标:N>0.2、VGCI>0.03。图8c中绿色背景区域即为综合性能最优区间,本设计选择图8c中坐标点(1.595,0.679)对应值作为尺度设计参数,根据式(26)、式(27)可求得如下三个量纲一参数:r1=0.679、r2=1.280、r3=1.042。参考人体双臂结构,设置d1=175 mm,可求得相应的尺寸参数。在对性能影响特别小的情况下,为加工制造方便,对求得的参数取整可得优化后的机构尺寸为d2=330 mm、d3=269 mm。
(a)N
5 机构性能分析
5.1 工作空间分析
由于该机构支链少,故其工作空间主要受限于两驱动球铰和三个虎克铰的运动范围。本文采用文献[23]所设计的球面运动发生器作为主动球副,其倾斜角运动范围为±60°,滚转角度则不受限制,即
0.5≤cosαicosβi≤1
(29)
如图9所示,连杆1和连杆2由虎克铰相连,θ1、θ2分别为两杆的旋转角,易知连杆2相对于连杆1的旋转矩阵为
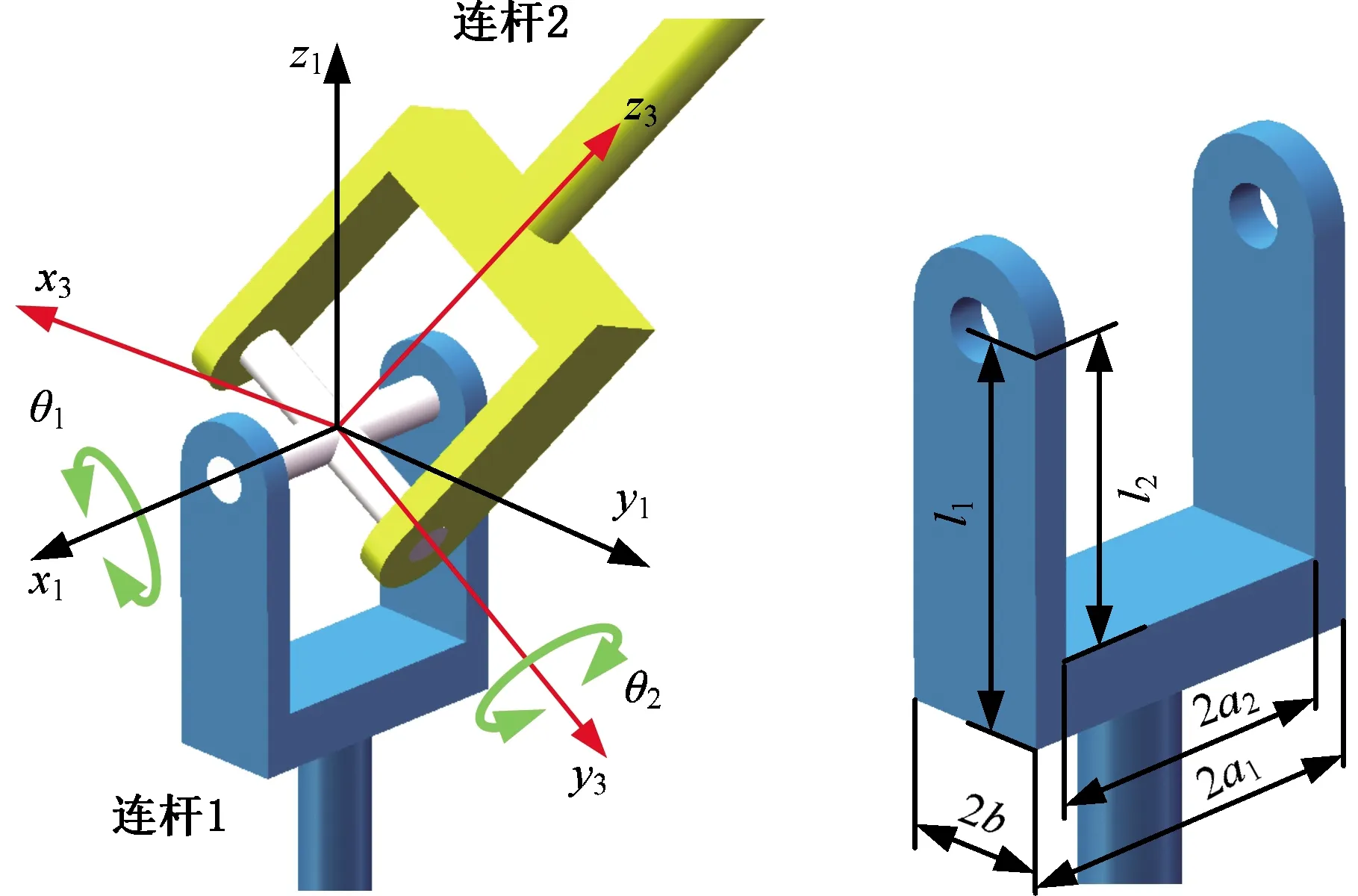
图9 虎克铰三维模型及几何尺寸
B=Rx(θ1)Ry(θ2)=
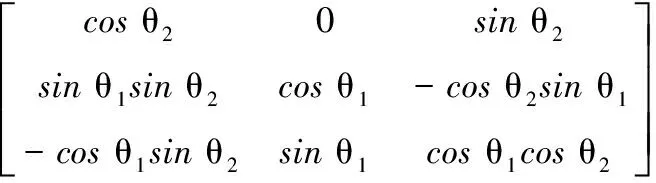
(30)
连杆1和连杆2相对于定坐标系的姿态矩阵分别为R1和R2,则连杆2相对于连杆1的旋转矩阵也可表示为
(31)
根据式(30)可得
(32)
其中,Bij为矩阵B的第i行、第j列的元素。
本文中虎克铰的结构参数为a1=25 mm、a2=20 mm、l1=50 mm、l2=40 mm、b=10 mm,根据文献[24],可计算得虎克铰的干涉曲线及工作空间,如图10所示。
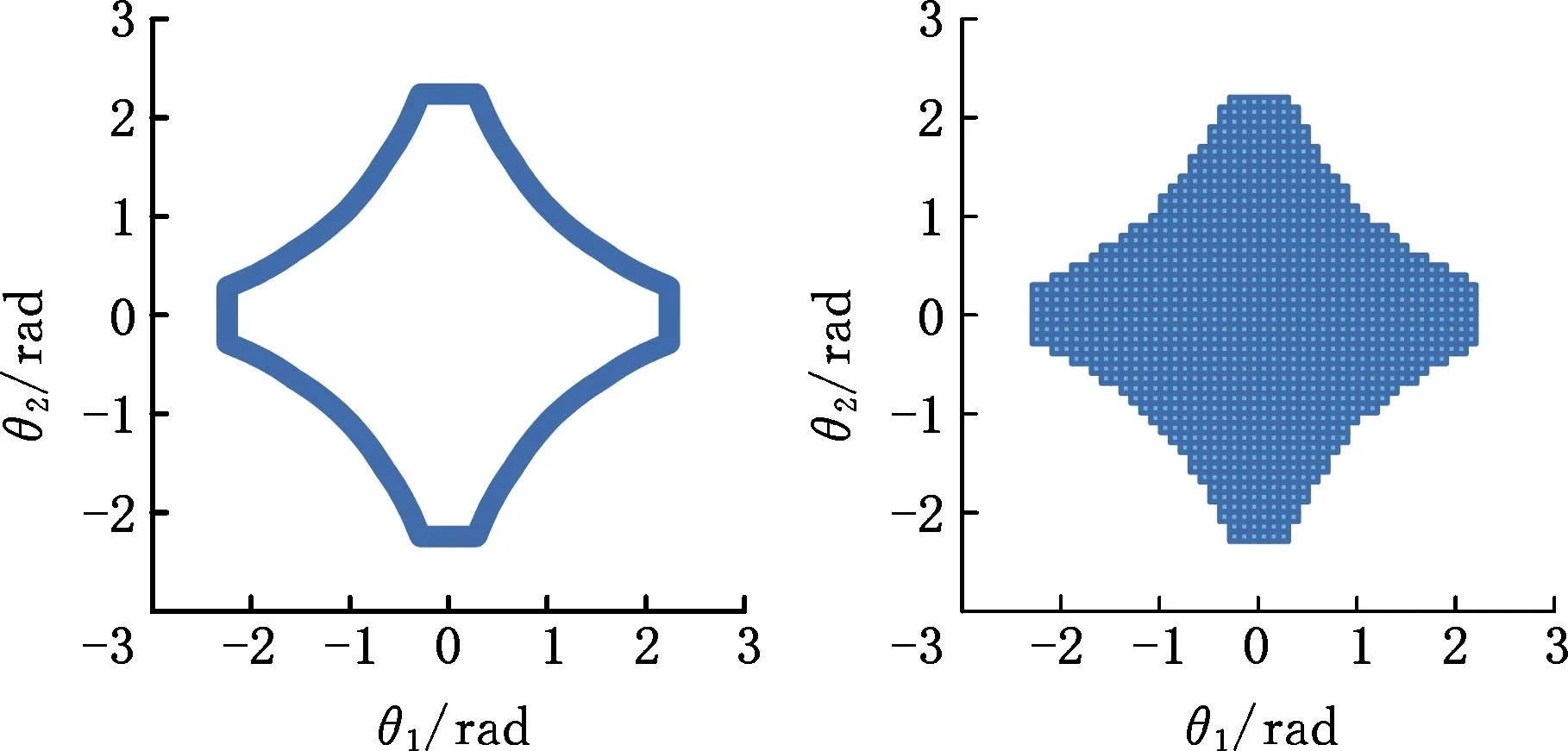
(a)干涉曲线 (b)工作空间
根据主动球副和虎克铰的工作空间,由运动学逆解,可计算得到机构的可达工作空间,如图11所示,其为一个畸形外凸面,内部存在两个关于平面X=0对称的类椭球状空腔。图12a~图12c所示分别为可达工作空间在XOY、XOZ、YOZ三平面上的投影轮廓,可以看出,该机构各方向的最大可达范围为:X∈[-390,400]mm、Y∈[-539,539]mm、Z∈[-151,562]mm,体积为0.206 m3。
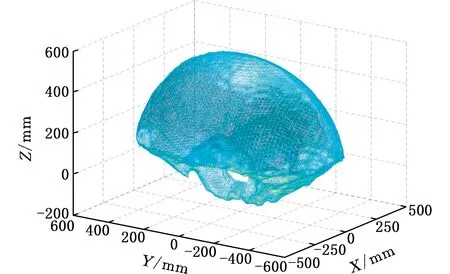
图11 三维实体透视图
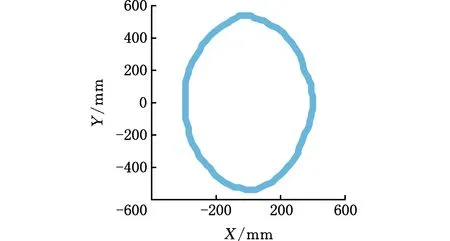
(a)XOY平面投影
为便于研究该机构末端位置处于零姿态(α=β=γ=0°)时的运动性能,图13给出了零姿态下机构的位置工作空间。相比于可达工作空间,由于各关节的限制,该机构的位置工作空间体积相对较小,为0.035 m3。
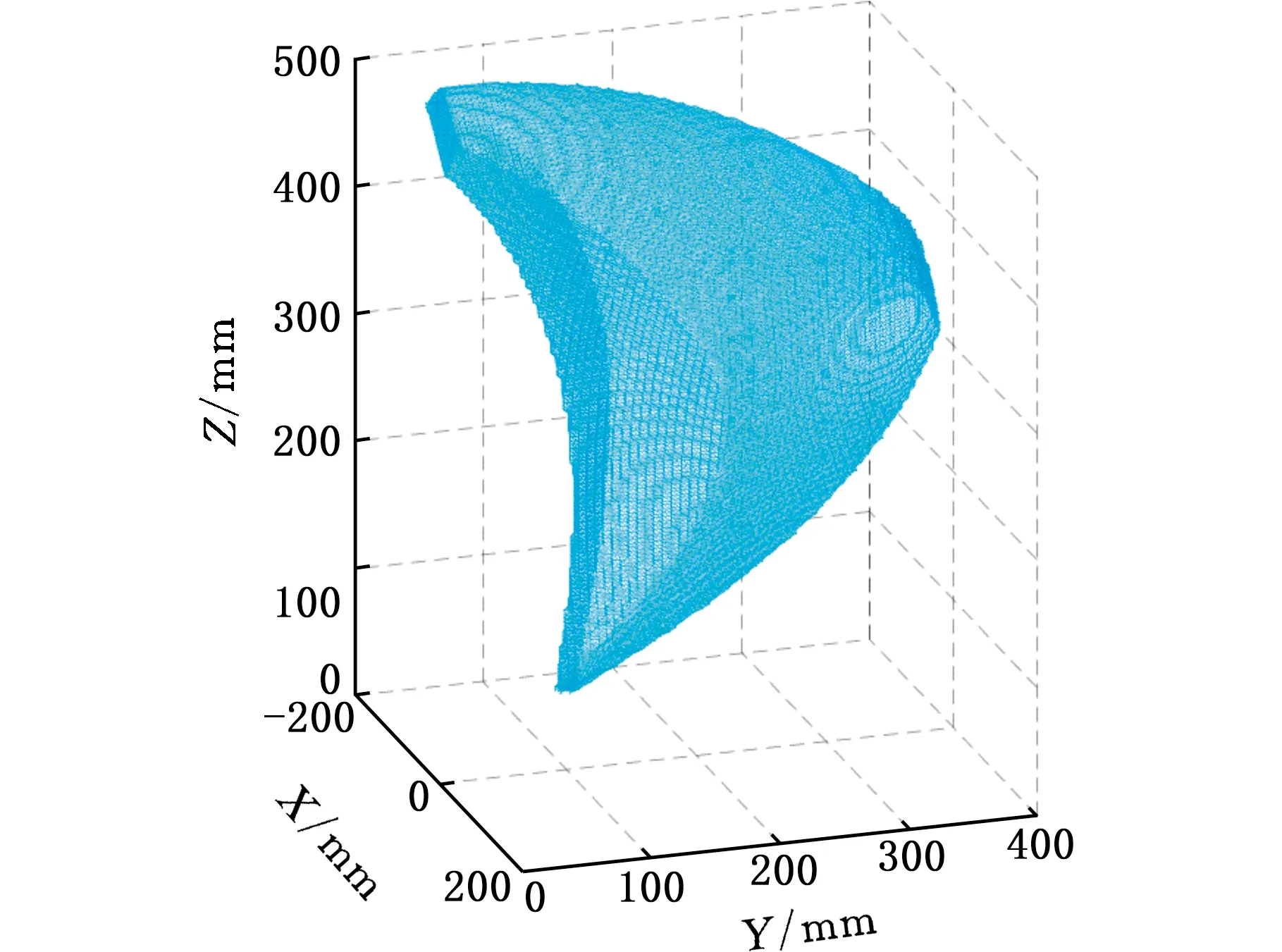
图13 零姿态下位置工作空间
在文献[25]所述的尺寸参数下,将本机构与传统6-RUS机构进行对比,分析发现与6-RUS机构相比,本机构的可达工作空间体积增大了58%,如表2所示。
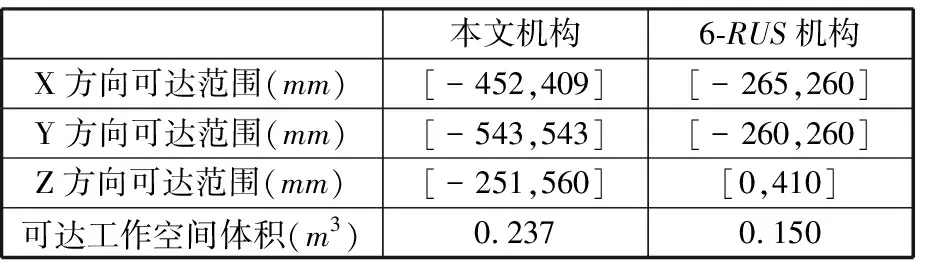
表2 可达工作空间对比
5.2 灵巧度性能分析
通过对机构局部条件数指标LCI进行分析计算,可得到它在位置工作空间内不同平面上的分布情况,如图14所示。
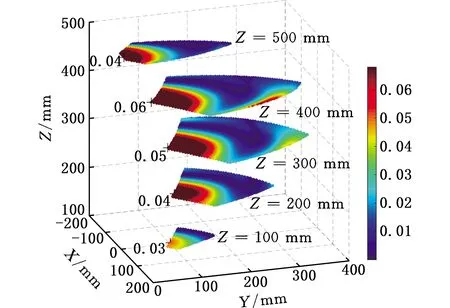
图14 零姿态下LCI分布
本文选择LCI值VLCI处于0.04~0.06区间内时作为灵巧工作空间[26]。由图14分析可知,各工作平面内的最优性能范围随Z值的增大而先增大后减小。当Z=400 mm时,灵巧工作空间的范围达到最大,占该工作平面的22.89%。图14还给出了各工作平面上的最大灵巧度指标值。在灵巧工作空间内,机构的性能指标变化平稳、连续,未出现突变,表明机构在该范围运动时具有较好的运动性能。
5.3 承载能力性能分析
对机构的最小承载力‖Fmin‖进行分析计算,可得到它在位置工作空间内不同平面上的分布情况,如图15所示。
在零姿态位置工作空间内,承载力性能指标‖Fmin‖的分布与灵巧度性能相似,其幅值变化较小,分布均匀。‖Fmin‖处于0.4~0.6区间内时,机构的承载力性能相对较好,此时为工作平面上的最优承载能力工作空间。由图15分析可知,处于Z=200 mm平面时,最优承载能力工作空间最大,占该工作平面的12.02%。各工作平面内‖Fmin‖的最大值已在图15中给出。在最优承载能力工作空间内,承载力性能指标变化较为平稳,表明机构具有良好的承载能力。
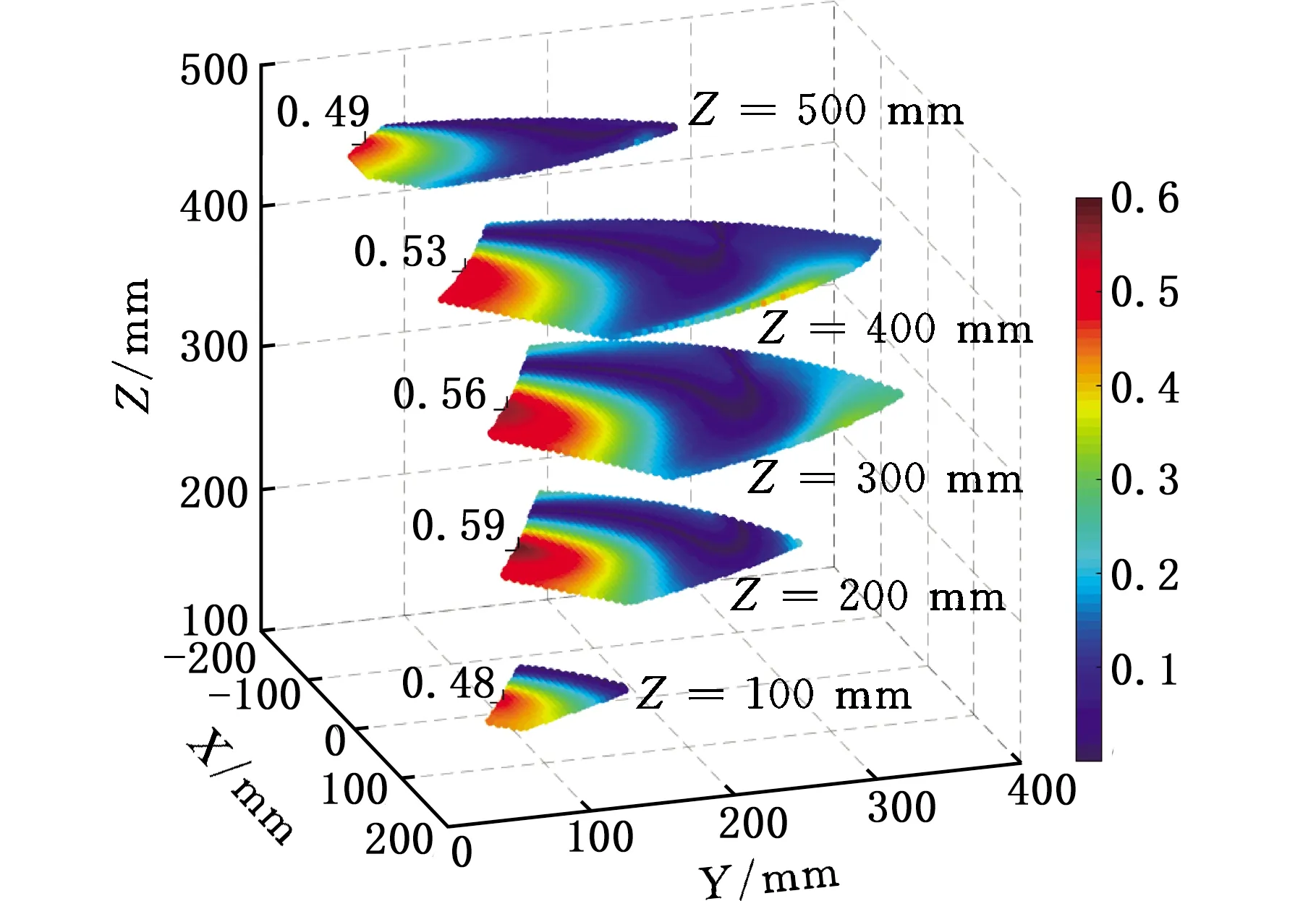
图15 零姿态下‖Fmin‖分布
5.4 刚度性能分析
本文取k=1000 N/m[19],对该机构的局部刚度指标LSI进行分析计算,得到了Z=400 mm工作平面内机构在各方向上LSI的分布情况,如图16所示。
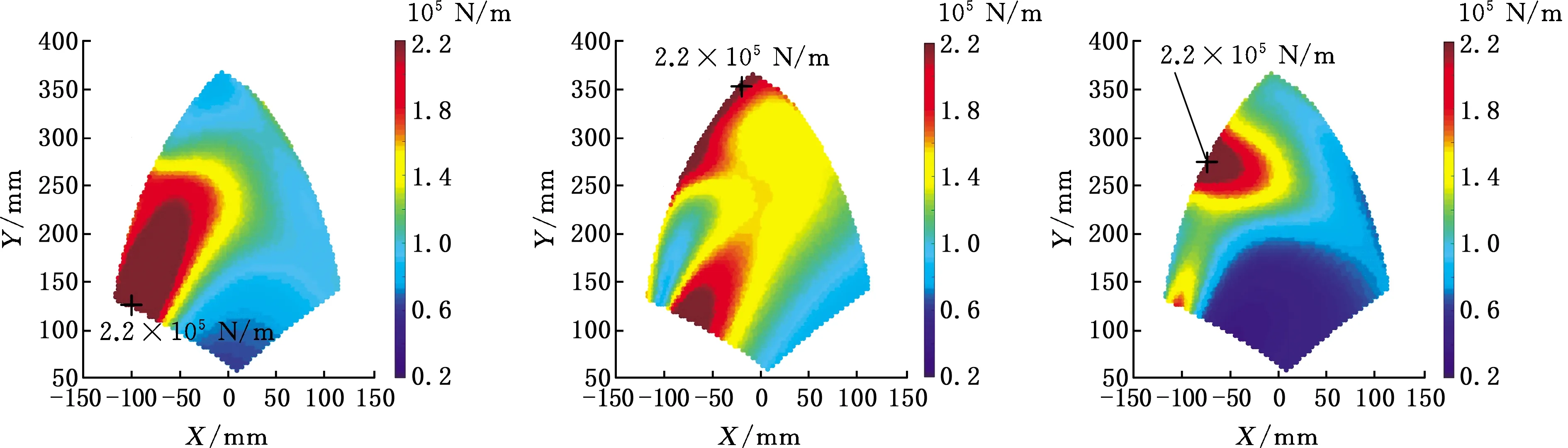
(a)x方向 (b)y方向 (c)z方向
从图16中可以看出,各方向上的局部刚度分布并不对称。x、y、z方向上的刚度在0.2×105~2.2×105N·m内变化,X<0时的刚度普遍高于X>0时的刚度。机构处于零姿态时,可观察到α、β、γ方向上的刚度变化范围分别为0.2×103~1×103N·m/rad、0.4×103~2×103N·m/rad和0.6×104~1.6×104N·m/rad。相对而言,γ方向具有更好的刚度性能。
6 机构的应用
图17所示为该机构的3D打印样机模型,它能实现六个自由度的运动,同时其结构相对紧凑。为实现球副驱动功能,可采用球面运动(spherical motion generator,SMG)[27]作为主动球副,如图18所示,SMG本质是一个3-RRR球面并联机构,其末端输出的球面运动即可作为本机构的主动球副输入。

图17 3D打印样机模型
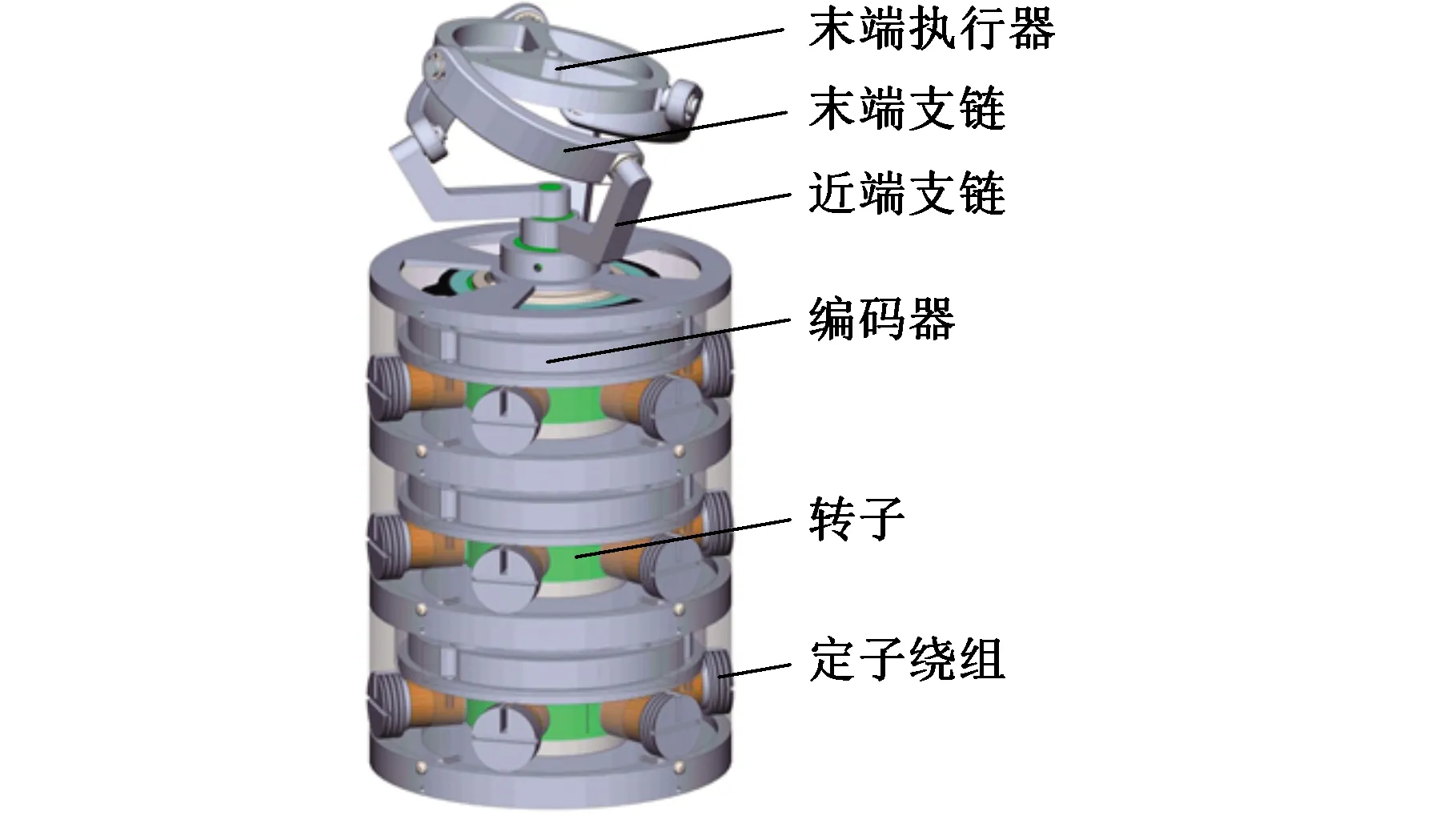
图18 球形运动发生器
如图19所示,将该机构作为人体外骨骼或运用到上肢康复训练中,能够有效地模拟人体肩、肘、腕关节的联合运动,与常规的康复机构相比,其结构更简单,安装空间更紧凑,便于控制同时保障其运动性能。
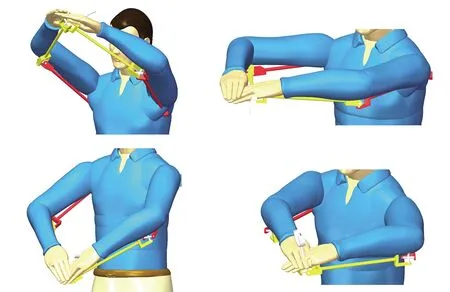
图19 上肢康复
在风洞试验中,受阻塞效应的影响越小,试验结果的准确性越高,将来流方向被测模型的投影面积与风洞试验段截面积的比值(即阻塞比)作为衡量标准[28]。相比于传统的试验装置[29],该机构的投影面积得到了进一步缩小,使在同等截面大小的风洞中阻塞比由5.40%下降至2.03%,如图20a~图20c所示。故本文所设计的机构可运用于风洞试验,两支链机构在拥有较大工作空间的同时,结构紧凑简单,能有效减小阻塞比,进而可保证风洞试验的准确性。
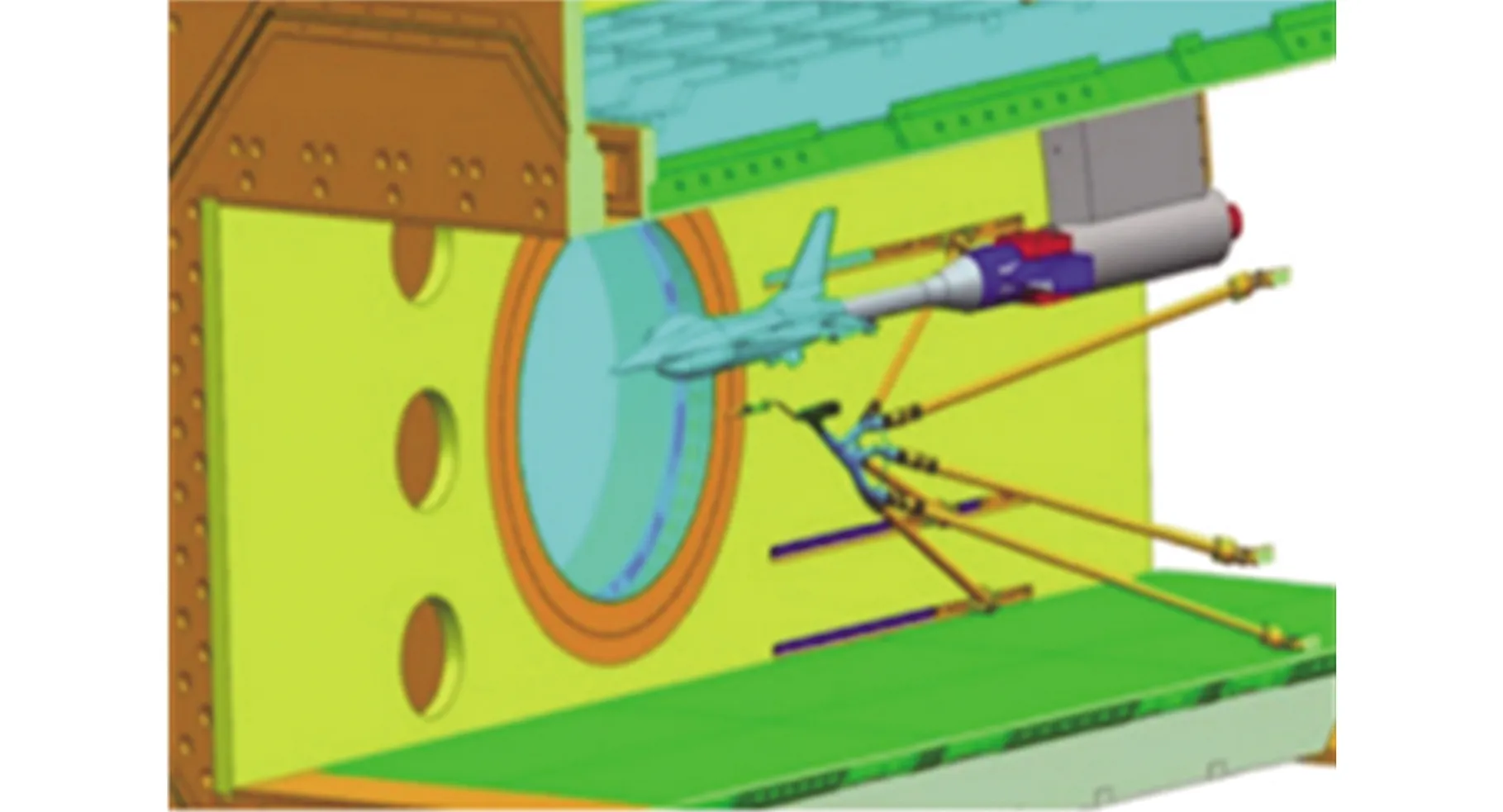
(a)传统风洞试验装置三维模型
7 结论
(1)提出了一种新型双支链六自由度并联机构,在描述了该机构组成及特点的基础上,对该机构进行了位置分析得到其位置逆解并求解出了雅可比矩阵。
(2)基于工作空间大小和运动灵巧度性能指标,利用性能图谱法完成了所提机构的尺度设计,得到了符合工程实际的尺寸参数。
(3)结合各关节的约束条件获得了所提机构的可达工作空间,对其灵巧度、承载能力及刚度性能指标进行了分析并作出了性能图谱。
(4)区别于传统六自由度并联机构,所提机构只有两条支链,结构更紧凑,工作空间得到了扩展,可望在康复、风洞试验等相关领域得到有效应用。
