恒压输出多负载无线电能传输系统分析与设计

孙淑彬，张 波，肖文勋，丘东元，陈艳峰

（华南理工大学电力学院，广州 510640）

无线电能传输WPT（wireless power transfer）技术作为近二十年来电力变换领域的研究热点[1-3]，给人们的生产生活带来了极大便利。2007 年，麻省理工学院的研究团队提出一种谐振式WPT 技术，实现了电能在发射端与接收端无任何线缆接触下的高效传输[4]。此后，不少学者开始把研究焦点转移到谐振式多负载WPT 技术[5-7]上来。然而，谐振式多负载WPT 系统的输出具有负载敏感性问题[8-9]，对其应用造成不良影响，尤其在等效电阻变化较为明显的应用场合（例如电池），需要额外增加通信电路和设计复杂的控制策略来实现所需的充电效果[10-11]。

文献[12]采用一个立方体结构的亥姆霍兹线圈来产生空间均匀磁场，将充电设备放置在立方体内即可进行无线充电，这种方式可在一定程度上克服负载敏感性问题，但无法满足负载变化较大的场合；文献[13]提出了一种可为LED 供电的多负载WPT 系统，其中采用LCC 拓扑对发射侧进行补偿，而负载全部并联在接收侧，然而这种方案无法满足负载需要隔离的场合；从控制的角度出发，文献[7]利用DC/DC 变换器对负载阻抗进行控制，使系统工作在最优负载状态，从而实现系统效率最大化；同时，基于博弈论的控制策略，可实现多负载WPT系统输出功率的自动调节[14]。然而，文献[7]和文献[14]均未考虑不同接收线圈与平面发射线圈之间的距离变化。

在WPT 系统中引入阻抗匹配网络IMN（impedance matching network），是解决负载敏感性问题的有效方法。对于单负载WPT 系统，已有不少学者做了大量研究，他们在WPT 系统的发射侧或接收侧引入必要的无源IMN，从而实现电压或电流的恒定输出[15-19]。

本文从单负载WPT 系统的角度，分别在发射侧和接收侧引入L 型、T 型或π 型阻抗匹配网络，并基于二端口网络理论，在合理假设的前提下分析并推导恒压输出单负载无线电能传输CS-WPT（constantvoltage-output single-load WPT）系统的电路参数统一表达式；同时归纳出所有满足要求的补偿网络，并将其扩展到恒压输出多负载无线电能传输CM-WPT（constant-voltage-output multi-load WPT）系统，随后分析所提多负载WPT 系统的传输特性。此外，应用有限元分析软件设计出具有磁场解耦特性的传输线圈机构，由此构建一种各负载功率均可独立调节的CM-WPT 系统，最后搭建样机，验证理论分析的正确性和所提系统的可行性。

1 CS-WPT 系统分析

在功率变换器中，通常将恒压输出列为重要的设计目标之一。传统的串联或并联谐振式WPT 系统具有负载敏感性问题，一种可行的解决方案是在系统工作频率固定的情况下，在发射侧或接收侧添加无源IMN。该方案可在实现高效无线电能传输的同时，实现输出端的负载无关特性，最终输出恒定电压。

无源补偿恒压输出的基本思路是通过无源IMN 来调节二端口网络的戴维宁（Thevenin）等效电路输出阻抗为0。常见的无源IMN 有L 型、T 型和π 型，相比之下，后两者有3 个可调节的元件，自由度更高，但前者只有2 个元件，元件数量较少，因此其各有优缺点。

CS-WPT 系统二端口网络等效电路如图1 所示。图1（a）中，CS-WPT 系统的接收侧仍然采用串联补偿电路，而在其发射侧的逆变电路和发射线圈之间添加了L 型、T 型或π 型IMN，Zn、Zk与Z1、Z2、Z3及Za、Zb、Zc分别为L 型与T 型及π 型IMN 的阻抗；在图1（b）中，IMN 位于接收侧，发射侧采用串联补偿电路。

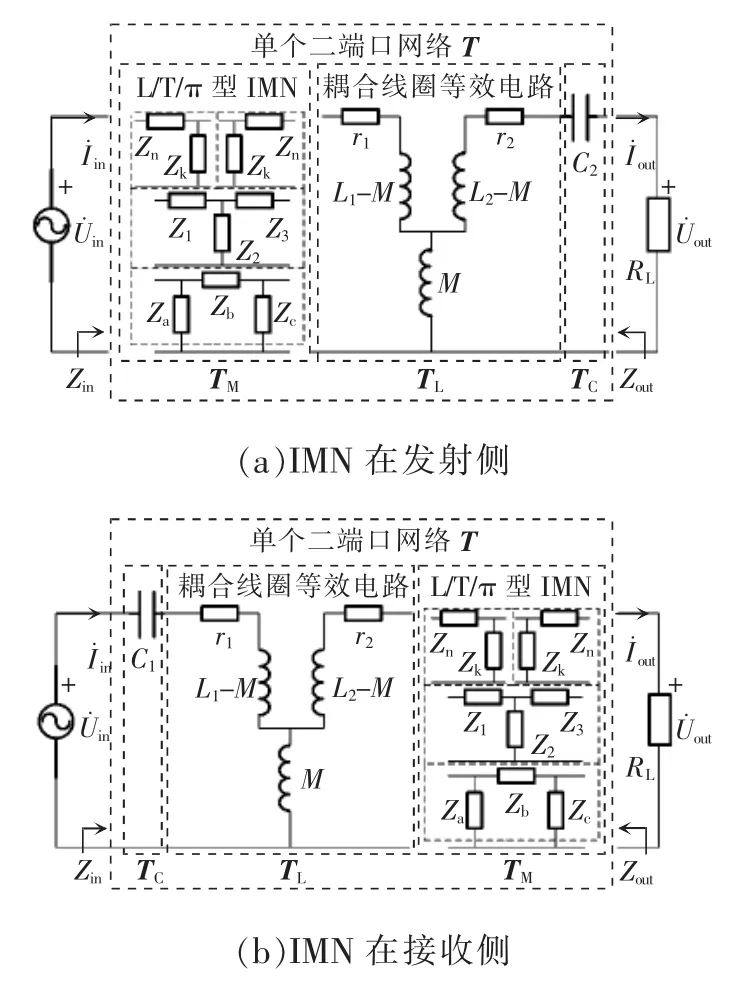
图1 CS-WPT 系统二端口网络等效电路Fig.1 Equivalent circuit of two-port network in CSWPT system

CS-WPT 系统由5 个部分组成，分别为逆变器、L/T/π 型二端口网络TM、耦合线圈二端口网络TL、电容二端口网络TC以及负载RL，其中TC、TL和TM组成单个二端口网络T。为简化分析，忽略线圈寄生内阻r1和r2，当IMN 在发射侧时，其参数矩阵为

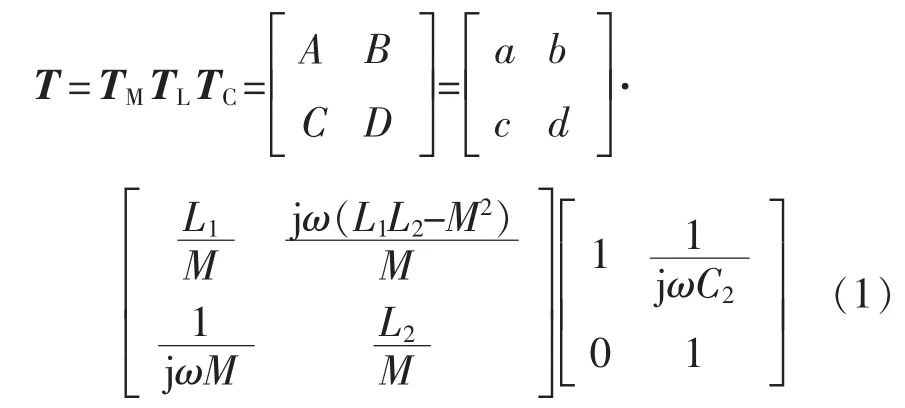
式中：A、D 为无量纲的比例系数；B、C 为阻抗和导纳；L1和L2分别为发射线圈和接收线圈的电感；M为L1和L2之间的互感；C2为接收侧的补偿电容；ω为系统工作角频率。

因此，图1 所示的CS-WPT 二端口网络输入和输出之间的关系可用矩阵表示为

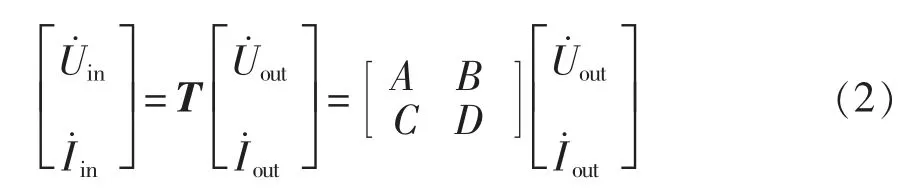
当忽略逆变器的内阻时，该WPT 系统整体的输入和输出阻抗、电压增益G 和传输效率η 分别为

设计接收侧工作在串联谐振状态，即1/L2C2=ω2，可提高系统的传输效率，则式（1）可简化为

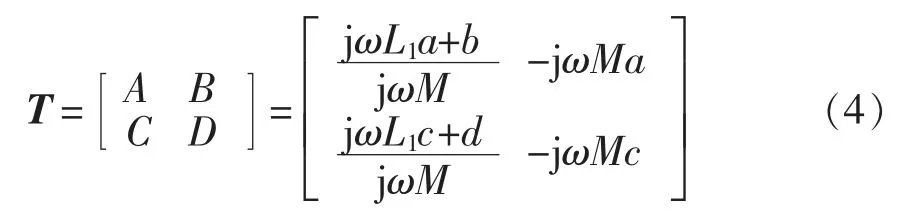
令Zout=0，输入功率因数为1，从而减少对电网的干扰，有Im（Zin）=0，由此可得，B=C=0，G=1/A。当忽略系统损耗即η=100%时，有AD=1，最终可得

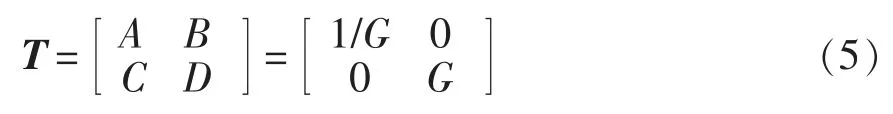
根据式（4）和式（5），IMN 的T 矩阵统一表示为

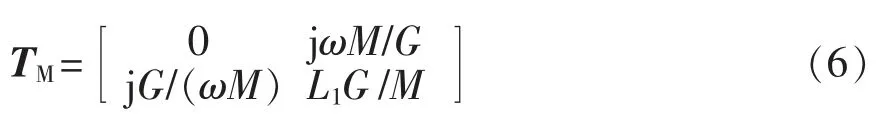
同理，IMN 在接收侧时其T 矩阵统一表示为

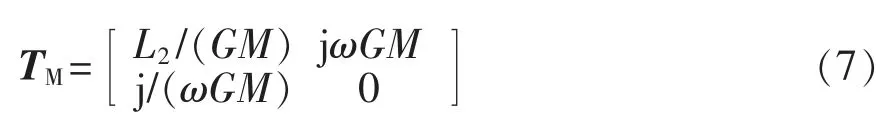
根据L 型阻抗的方向，可将L 型IMN 分为左L型和右L 型，推导出各类无源IMN 的T 矩阵表达式如表1 所示，其中，输入电压/电流以朝向二端口网络为参考方向，而输出电压/电流以二端口网络朝外为参考方向。

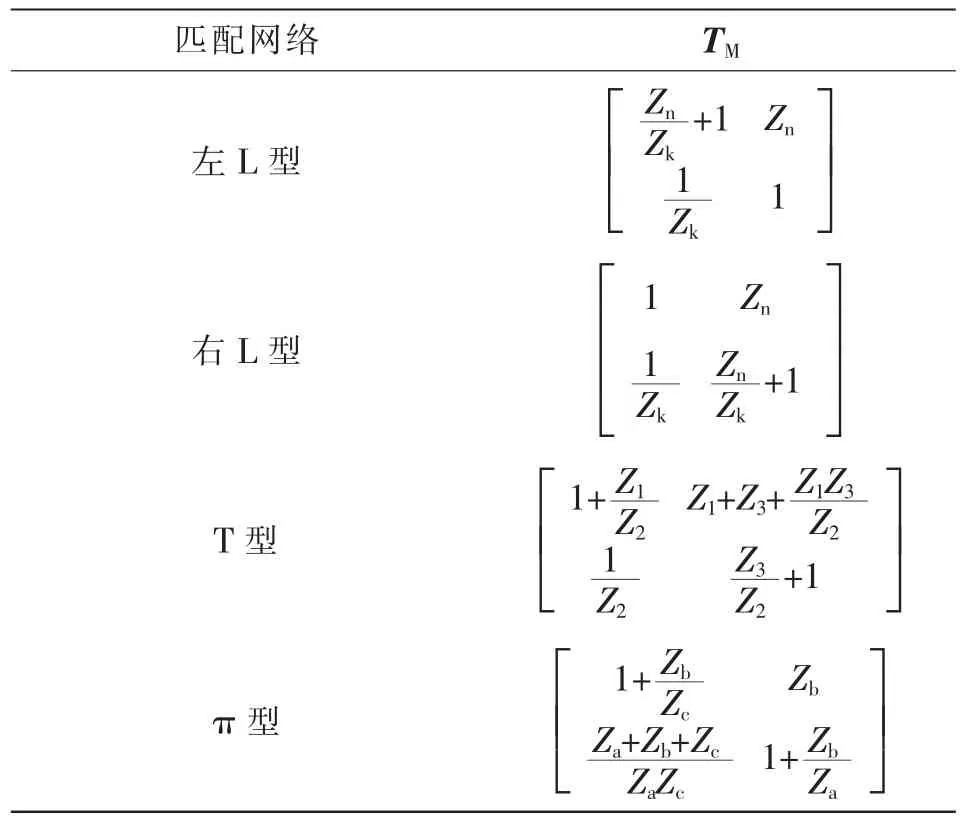
表1 4 种匹配网络的TM 矩阵Tab.1 TM matrixes of four kinds of matching network

结合式（6）、式（7）和表1，可推导出T 型和π型匹配网络中各无源器件的具体表达式，而假设发射侧或接收侧处于串联谐振状态下，左L 型和右L型匹配网络各器件参数无法求得。

针对该问题，重新作前提假设，令1/（L2-M）C2=ω2，则式（1）可简化为

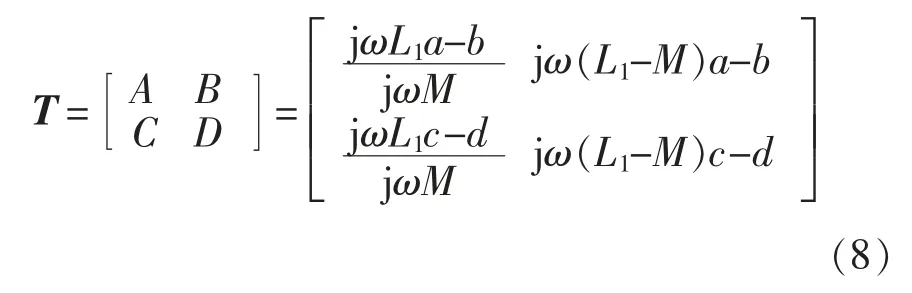
由式（5）和式（8），匹配网络T 矩阵统一表示为

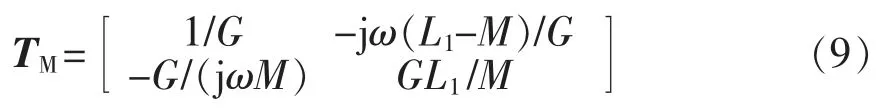
当匹配网络在接收侧时，其T 矩阵统一表示为

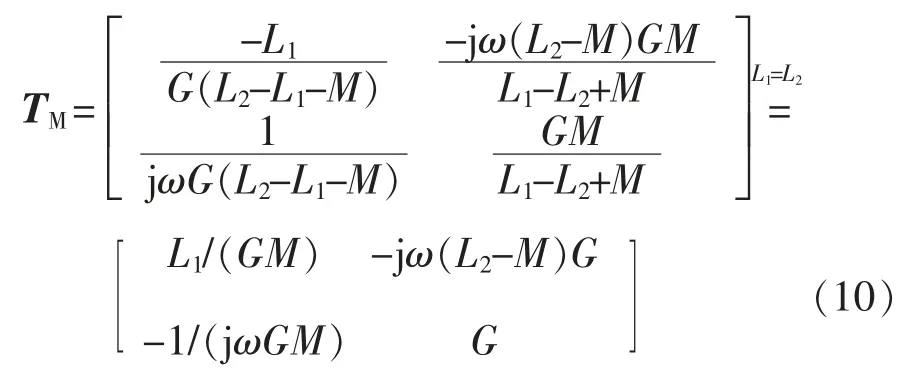
当电压增益G 不同时，IMN 的具体拓扑、工作条件、补偿电感数量和系统电压增益G 如表2所示。因此，IMN 分别在发射侧或接收侧时各元件的具体参数可推导如下。

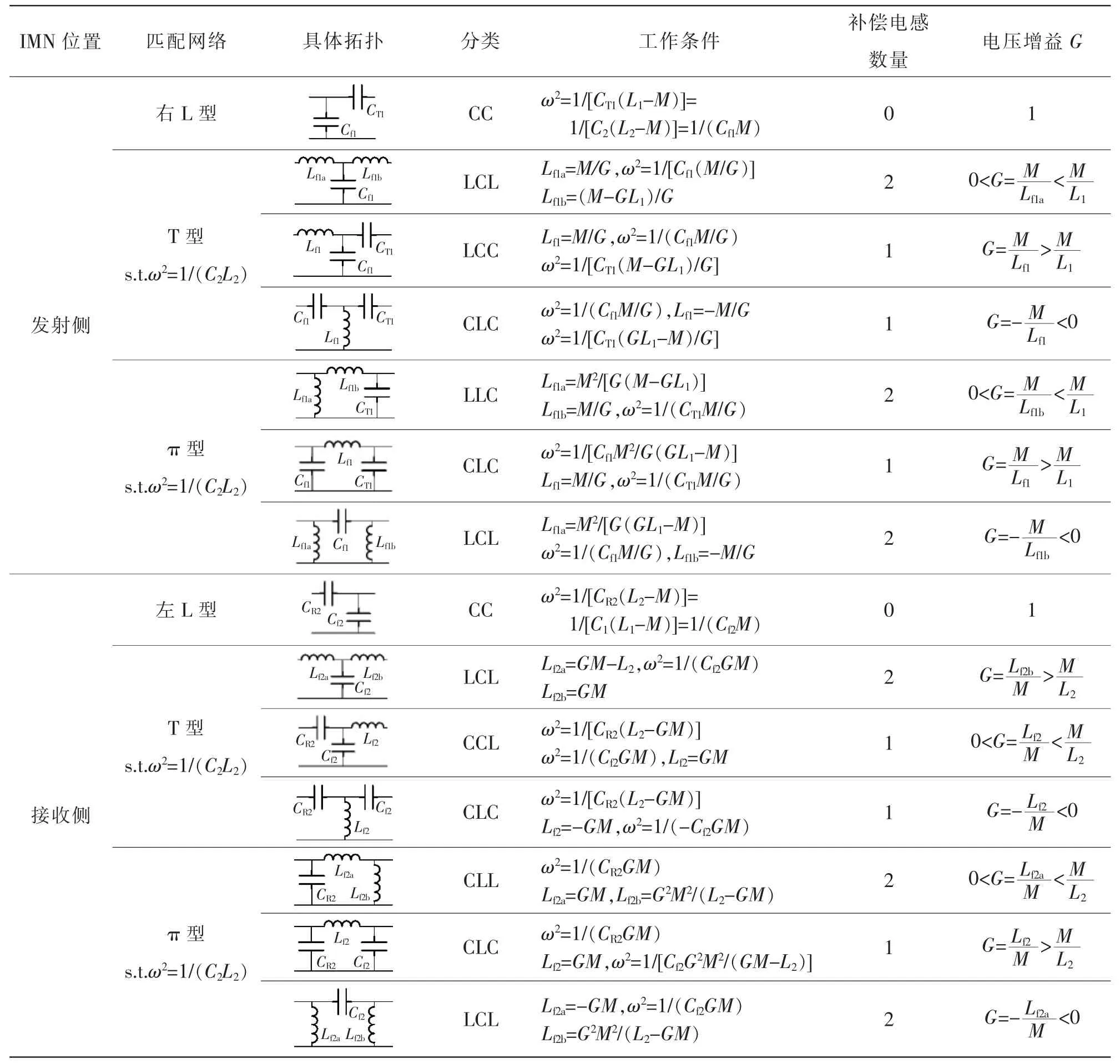
表2 不同位置添加不同匹配网络的拓扑对比Tab.2 Comparison among topologies with different matching networks added at different positions

若IMN 在发射侧，右L 型、T 型和π 型IMN 参数为

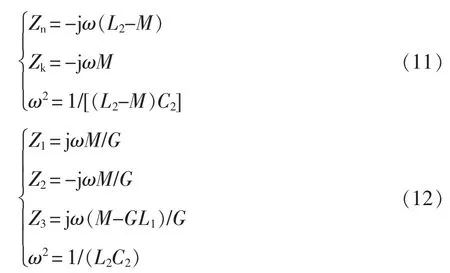
若IMN 在接收侧，左L 型、T 型和π 型IMN 参数为

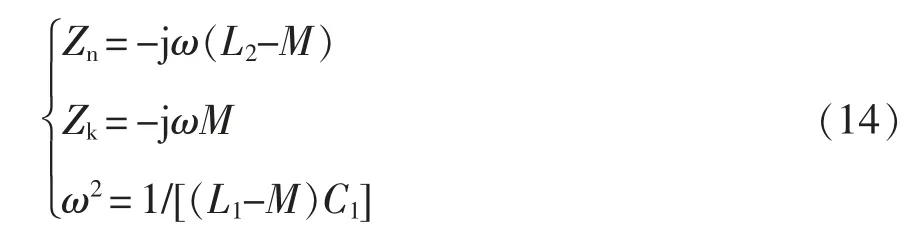
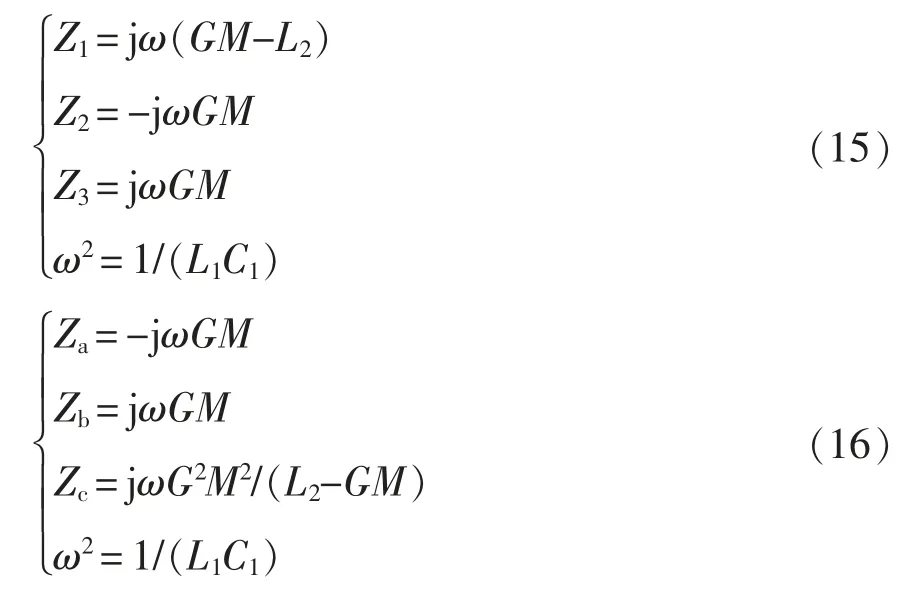
根据式（11）～式（16），可构造出至少14 种互感不变时的CS-WPT 系统。

2 CM-WPT 系统设计

2.1 级联式CM-WPT 系统构造

应用多个图1 所示CS-WPT 系统，通过级联的方式且仅保留第一级输入侧的交流源为系统供电，其余各级的输入均直接与前一级负载两端的输出相接。由于每一级的输出特性与负载无关，当第i-1级的接收线圈与第i 级的发射线圈之间的互感能够被忽略时，前一级和后一级只有电路联系，而没有磁场联系，因此每一级依然具备负载无关的输出特性，由此，可构造出一种级联式CM-WPT 系统。

在工作频率较高的情况下，线圈或补偿电感的趋肤效应和领近效应明显增强，从而产生更大的寄生内阻，加上补偿电感的磁芯损耗和可能发生的磁饱和现象，最终可能导致系统的电压损失较大、导线发热严重、系统效率低下和故障率提升。相比之下，补偿电容的高频寄生内阻较小，而且可以通过多个电容并联进一步得到优化，因此应该选择电感元件尽可能少的IMN。由表2 可知，当IMN 位于发射侧时，右L 型IMN 只有2 个补偿电容，无补偿电感；当IMN 位于接收侧时，左L 型IMN 同样无补偿电感。这2 种IMN 存在的缺点是其WPT 系统的电压增益为固定值，但在实际应用中，电压增益一般可选择为1，进而简化设计，因而能够满足基本需求。如果电压增益必须大于或小于1，则对比表2不同匹配网络，可优先选择T 型IMN，主要因为当其电压增益设计为负数时，CLC 型IMN 的补偿电感数量达到最少。

2.2 CM-WPT 系统建模

选择右L 型IMN 并通过第2.1 节方法构造出一种CM-WPT 系统，如图2 所示。图3 为对应的互感模型等效电路。其中：为系统输入电压相量；为第i 个负载输出电压相量（i=1，2，…，N）；Ri表示负载；LT0和LTj分别为发射单元0 和中继单元j 的发射线圈电感；Cf0、CR0、Cfj和CRj为其右L 型匹配网络的补偿电容；LRj和LRN分别为中继单元j 和接收单元N 的接收线圈电感；CRj和CRN为其补偿电容，下标j=1，2，…，N-1。此外，Mi和ki分别为第i-1 个发射线圈与第i 个接收线圈之间的互感和耦合系数，且有

图2 含有L 型匹配网络的CM-WPT 系统Fig.2 CM-WPT system with L-type matching network

图3 CM-WPT 系统的互感模型等效电路Fig.3 Mutual-inductance-model-based equivalent circuit of CM-WPT system

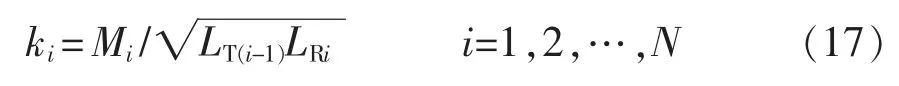
由上述分析可得，该系统的补偿电容满足的工作条件为

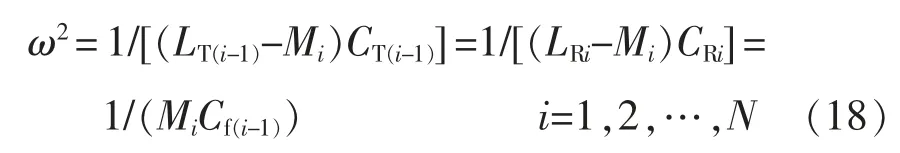
如果考虑线圈电感的寄生内阻rTi和rRi，根据互感模型[20]，LRi反射到LT（i-1）的等效反射阻抗可表示为

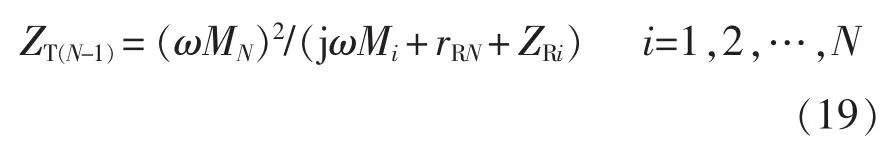
在式（19）中，ZRi的具体表达式为

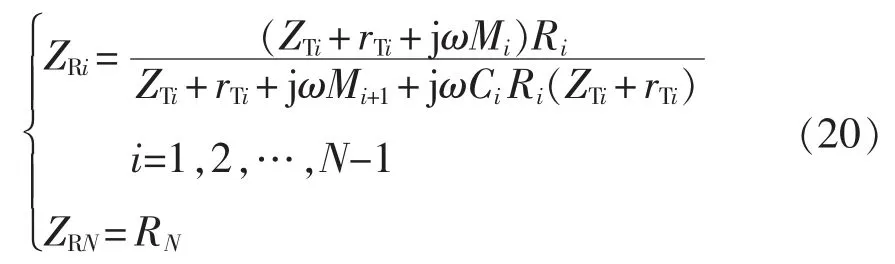
根据基尔霍夫定律，图2 中所示的电压和电流参数满足的关系为

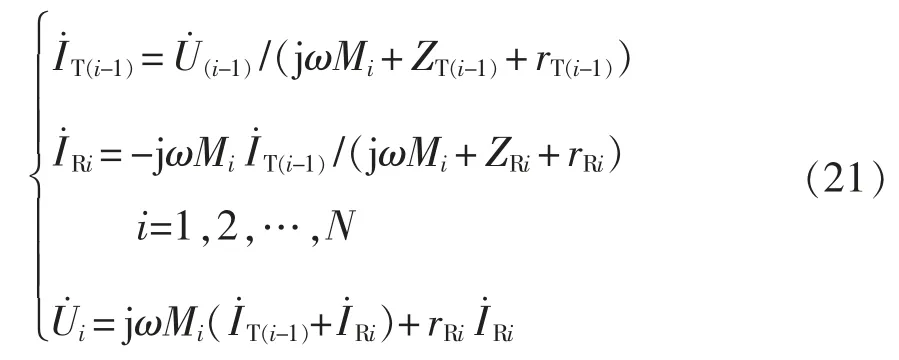
根据式（21），该系统的传输效率可表示为

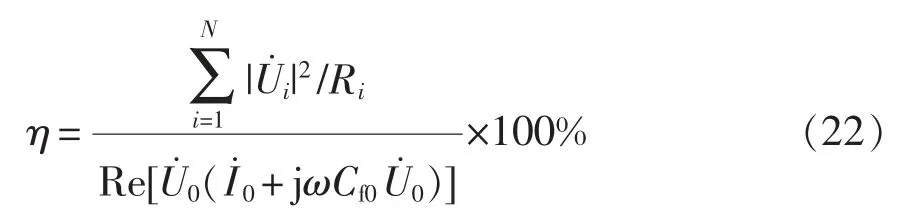
通过MATLAB 对式（19）～式（21）进行迭代计算，可得该系统的理论输出电压和输入电流，并由式（22）获得传输效率。

在实际应用中，当线圈电感的品质因数Q（Q=ωL/r）足够高时，其寄生内阻可忽略不计，负载Ri两端输出电压与前端输入电压的关系为

同时，令所有线圈电感和互感的取值各自相同，即LT1=LT2=…=LR（N-1）=LRN，MN=MN-1=…=M1=M，理论分析表明，当满足式（18）时，该系统的所有输出与输入电压幅值和相位均相同且与负载无关。

3 线圈设计

3.1 磁场解耦原理

图4（a）描述了一种被称为DD 线圈的绕线方法[21]，该类线圈形状一般设计为方形以简化设计。当电流按照图示箭头的方向流过导线时，磁场通过线圈右半平面穿入，并从左半平面穿出，图中“⊗”和“⊙”分别表示磁力线方向垂直平面线圈由外向内和由内向外。当2 个DD 线圈同方向放置时，磁场同时穿过它们的左半平面和右半平面，进而相互耦合。然而，当两者垂直方向放置时，其中一个线圈穿入和穿出另一个线圈的磁场几乎相等，所以两者之间呈现弱耦合甚至无耦合的特性，从而实现磁场解耦。根据这个原理，设计一种如图4（b）所示的解耦线圈结构，其中除了发射单元和接收单元采用单线圈结构，剩余所有中继单元均采用垂直放置的双线圈结构。该线圈的绕线方式会使其平均外径小于传统的单极方形平面螺旋线圈，导致其自感和线圈间互感相应减小。针对该问题，在所有单元中各嵌入一块方形铁氧体磁芯（型号为PC44）。所嵌入的磁芯不但改善了线圈间耦合，还对非相邻单元中同方向线圈之间的磁场形成屏蔽作用，加强解耦效果。

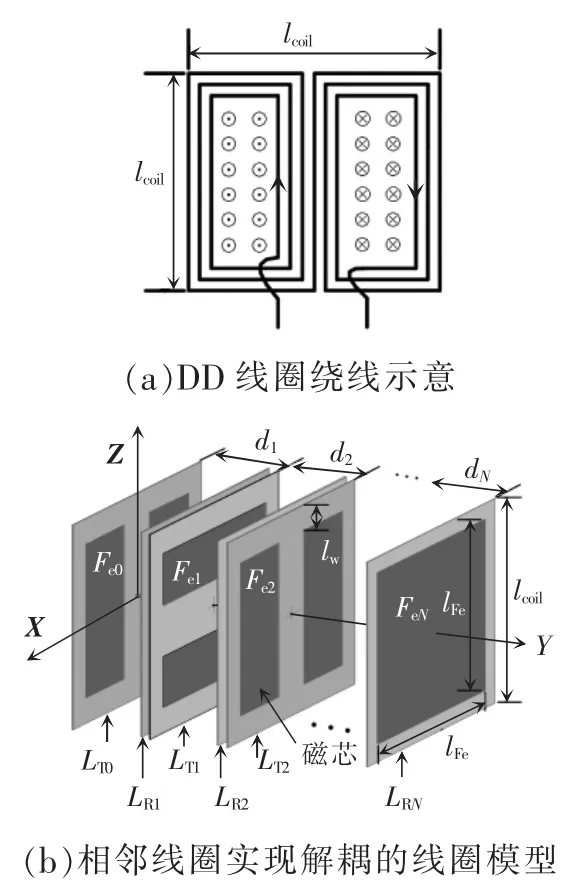
图4 解耦线圈机构Fig.4 Structure of decoupling coil

3.2 有限元分析

实现线圈之间耦合系数的最大化是线圈设计的一项重要指标，应用有限元分析软件将极大降低线圈的设计成本。文献[22]中已详细介绍如何利用Ansoft Maxwell 软件建立线圈的三维电磁仿真模型，从而得到不同线圈之间的互感、耦合系数以及各自自感。在高频条件下，趋肤效应和邻近效应会使得导线产生涡流损耗。1 MHz 以下工作频率的应用场合中，趋肤效应是造成涡流损耗的主要因素。通常情况下，采用多股并绕的利兹线可有效改善该问题。铜导线的趋肤深度δ=，其中，真空磁导率μ0=4π×10-7T·m/A，铜电阻率ρc=1.75×10-8Ω/m。令系统的工作频率f=200 kHz，可得δ=0.15 mm。参考利兹线在不同频段的规格推荐值[23]，同时保证导线电流密度小于5 A/mm2，可选取规格为φ0.1 mm×160 股的利兹线，其有效截面积为1.256 mm2，总外径为1.67 mm。

根据实际应用，设计线圈长度lw=160 mm，图5展示了传输距离为55 mm 时，线圈之间耦合系数k的仿真结果与磁芯长度lFe和不同线圈有效宽度lw的关系曲线。由于导线线径一定，所以不同lw代表不同导线匝数。由图5 可见，随着磁芯长度的增大，相同匝数的线圈之间的耦合系数先增大到某一峰值后逐渐下降；对于lw为10～25 mm 时，耦合系数的峰值发生在lFe=130 mm，在这一点上，当lw从10 mm 增大到20 mm 时，耦合系数相应增大；之后随着lw进一步增大，耦合系数反而减小。经过综合考虑，选择lw=20 mm、lFe=130 mm，以实现耦合系数的最大化。此时该线圈的寄生电阻为0.35 Ω，品质因数达到330。

图5 耦合系数与lw 和磁芯长度的关系（传输距离为55 mm）Fig.5 Relationship among coupling coefficient,lw and length of magnetic core（at transfer distance of 55 mm）

采用多个DD 线圈，按照图4（b）所示方式摆放，即可获得无磁芯的线圈机构；再将铁氧体磁芯嵌入图4（b）所示的特定位置，即可搭建出带磁芯的解耦线圈机构。当从侧视角度观察时，这2 种线圈机构的磁场分布仿真结果如图6 所示。对比图6（a）和图6（b）可以发现，磁芯对磁场的分布造成了极大影响。当线圈机构不含磁芯时，磁场较为分散地分布于每个线圈的两侧和线圈边缘，磁场分布范围较广，说明了该线圈机构产生的漏磁较多。从图6（b）可见，当将磁芯置于特定位置后，线圈无磁芯一侧磁场较小，磁场被主要约束于磁芯内，线圈机构的泄露磁场非常小，因而几乎不对周围环境造成电磁干扰。

图6 线圈机构的磁场分布仿真结果Fig.6 Simulation results of magnetic distribution in coil mechanism

为了进一步凸显解耦线圈机构的特点，添加了俯视角度和侧视角度的磁通分布，如图7 所示。由图可见，DD 线圈产生的磁通矢量分布方向与第3.1节中所分析的一致。由于铁氧体磁芯的屏蔽作用，磁通量几乎只在每一对同方向放置的发射线圈和接收线圈之间流动（比如LT（i-1）和LRi），而穿过磁芯到达另一侧（比如LTi和LR（i+1）之间）的磁通量非常小。若将kT（i-1）_Ri、kT（i-1）_Ti、kRi_Ti以及kRi_T（i+1）分别定义为LT（i-1）和LRi、LT（i-1）和LTi、LRi和LTi以及LRi和LT（i+1）之间的耦合系数，期望和非期望耦合线圈之间耦合系数的仿真结果如表3 所示。

图7 解耦线圈机构的磁通分布Fig.7 Magnetic distribution in decoupling coil mechanism

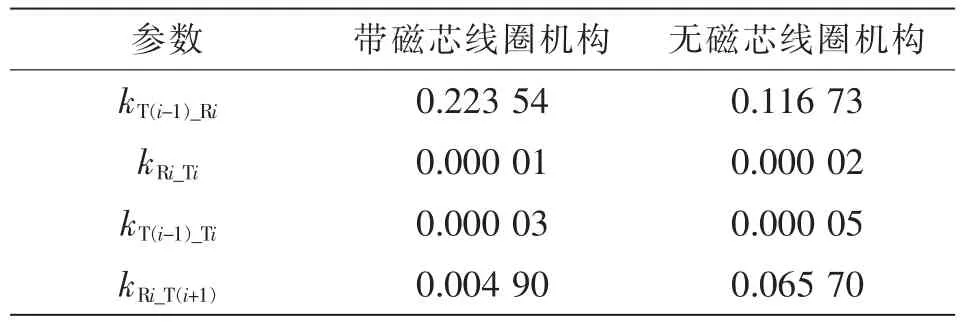
表3 期望和非期望耦合线圈之间耦合系数的仿真结果（传输距离为55 mm）Tab.3 Simulation results of coupling coefficient between expected and unexpected coupled coils（at transfer distance of 55 mm）

由表3 可知，在带磁芯和无磁芯的线圈机构中，期望和非期望耦合线圈之间的耦合强度存在明显差别。其中，对于期望耦合线圈之间，含有磁芯时耦合强度几乎是不含磁芯时耦合强度的2 倍。对于非期望耦合线圈之间，垂直放置的线圈（例如LRi和LTi，LT（i-1）和LTi）之间的耦合强度均足够小，而同方向放置的线圈（例如LRi和LT（i+1））之间耦合强度是否足够小取决于是否含有磁芯，带磁芯情况下该耦合强度要比不带磁芯情况下的耦合强度减小至1/10 以下。通过上述分析证明了磁芯对线圈机构的解耦效果起到了极为明显的增强作用。另外，图8 描述了各个耦合系数与传输距离的关系，其中的实线和符号分别表示仿真结果和实验结果。

图8 磁场解耦线圈机构的参数关系曲线Fig.8 Curve of parametric relationship for magneticfield-decoupling coil mechanism

4 实验结果

实测表明，NP0 或C0G 材质的贴片电容的高频寄生内阻要远小于其他材质的贴片电容，并且电容值的精度更高，同时其价格在大规模国产化的背景下变得足够低廉，本次实验选用NP0 或C0G 材质的贴片电容作为补偿电容。所有DD 线圈同轴放置，应用阻抗分析仪（型号为Wayhe Kerr 6500B）精确匹配补偿电容。选用寄生电容较小的MOSFET 构成逆变器主电路，用数字信号处理器（型号为TMS 320F28335）产生一个频率为200 kHz 的方波驱动信号，所搭建的恒压输出四负载WPT 系统样机如图9所示，具体的运行参数如表4 所示。图9 展示了所设计的解耦线圈机构、发射端电路PCB 正面和背面、数字控制电路等装置组成部分的细节，其实验波形由型号为RRTB2004 的数字示波器进行捕捉。

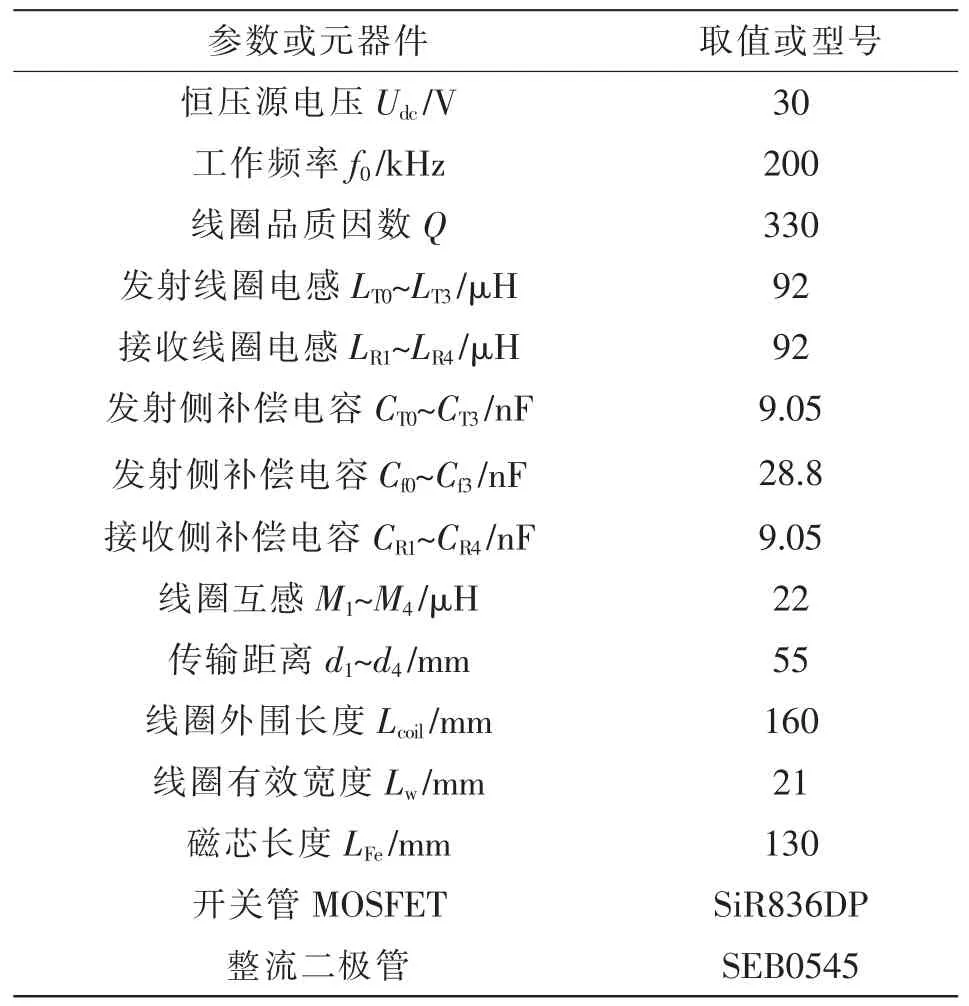
表4 系统实际运行参数Tab.4 Actual operation parameters of system

图9 恒压输出多负载WPT 系统实验装置Fig.9 Experimental setup of CM-WPT system

由于本次实验采用全桥逆变器，而系统处于谐振状态，所以其方波输出中只有基波含量作用于系统。基于傅里叶级数展开公式，逆变器输出电压的基波有效值可表示为

式中，Udc为全桥逆变器输入端恒压源电压。

为了研究系统的输出特性，图2 所示的Ri（i=1，2，3，4）均直接采用寄生参数较小的电阻作为交流负载。实验结果表明，金属氧化膜电阻的寄生参数较小，考虑到单个功率等级较小，可采用多个并联作为测试负载。未整流和整流后的输出电压波形如图10 所示。当负载电阻均为260 Ω 时，CM-WPT系统的逆变器、负载R2和负载R4两端输出电压的运行波形如图10（a）所示。由图10（a）可见，不同负载两端输出电压的相位相同，有效值几乎与逆变器输出电压的基波有效值相等，实验结果验证了上述理论。当Ri换成整流器、47 μF 的滤波电容和直流负载，且R1、R2、R3的直流负载分别为100、50、150 Ω 的电阻，而R4整流输出保持空载时，输出电压如图10（b）所示。结果表明，所有整流器输出端可获得几乎一致且恒定的直流电压，使其可满足大部分应用场合。

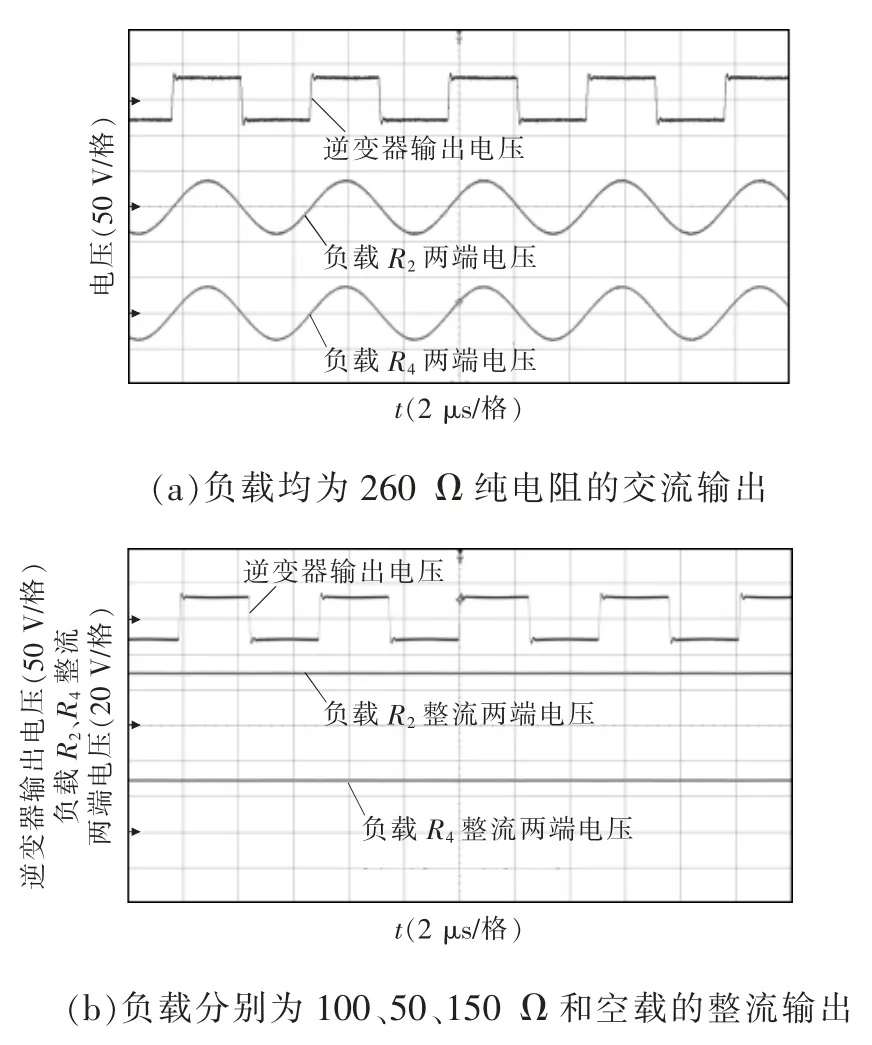
图10 未整流和整流后的输出电压实验波形Fig.10 Experimental waveforms of output voltage with and without rectification

图11 描述了当所有负载电阻一致时，系统稳定工作后各个输出电压和传输效率与负载电阻的关系。图中实线和符号分别表示理论结果和实验结果。如图11 所示，由于线圈内阻或功率器件产生损耗，因此负载两端的输出电压相比于输入电压有一定的衰减，且级数越高或输出功率越大，电压衰减越严重。从图11 可以看出，当所有负载电阻同时从400 Ω 减少到50 Ω，即总输出功率从7.2 W 增大到48.4 W 时，负载R1两端电压从27.0 V 下降到25.8 V，电压变化率为4%；而R4两端电压从26.6 V下降到23.8 V，电压变化率达到10%。考虑到该系统电压增益为1，即空载情况下输出电压约为27 V，所以在输出功率为48.4 W 时，R4两端的电压衰减率最大，达到11.9%。

系统的各个输出接上不同阻值的负载电阻，可进一步验证CM-WPT 系统的输出特性。图12 给出了不同负载条件下，各个输出电压和传输效率与负载R4的关系，其中，R1、R2、R3分别为50、150、300 Ω。当R4从400 Ω 减小到50 Ω 时，R4两端电压从26.0 V 下降到24.9 V，电压衰减率最大，达到7.8%。结果表明，鉴于单个负载变化造成的输出功率变化范围有限，系统的各个输出对负载呈现出更低的敏感度。同时，各个负载的输出功率可独立调节，而几乎不对其余负载造成干扰。虽然输出功率较大时所提系统存在电压衰减，但随着导线材料的改善，该问题将得到有效解决。此外，图11 和图12所描述的效率曲线表明，系统的传输效率随着输出功率的增大先上升后降低，并在某个输出功率值时达到峰值，说明该系统存在最优负载。根据实验结果，当系统的总输出功率为16～36 W 时，传输效率均大于90%，而在最优负载处达到92.2%。

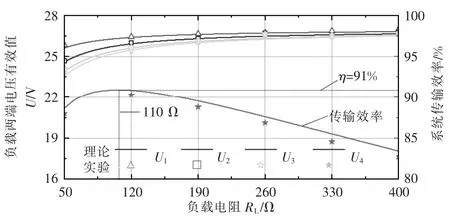
图11 多恒压输出WPT 系统性能与负载的关系（R1=R2=R3=RL）Fig.11 Relationship between CM-WPT system performance and load（R1=R2=R3=RL）

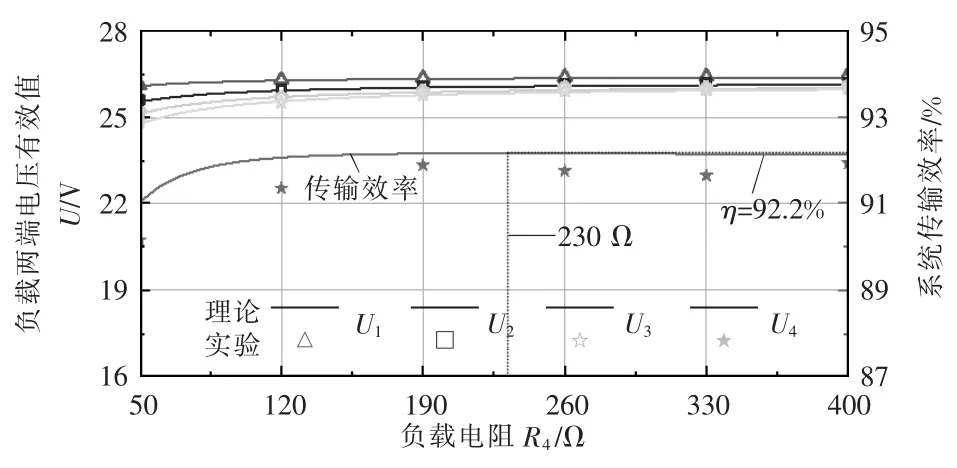
图12 CM-WPT 系统性能与负载的关系（R1=50 Ω,R2=150 Ω,R3=300 Ω）Fig.12 Relationship between CM-WPT system performance and load（R1=50 Ω,R2=150 Ω,R3=300 Ω）

5 结语

本文针对谐振式WPT 系统存在的负载敏感性问题，分析并设计了一种各个输出均与负载无关的级联式CM-WPT 系统。理论分析结果显示了L 型、T 型和π 型匹配网络均能够在满足特定谐振条件下使得系统具有恒压输出的特性，其中L 型匹配网络不含补偿电感，元件数量最少，而T 型和π 型匹配网络均至少含有一个补偿电感。所设计的解耦线圈机构能够实现非期望耦合线圈之间的磁场解耦，满足设计需求。所提CM-WPT 系统无需任何复杂的控制策略，依然能够给有电气隔离和功率独立调节等需求的多个负载供电。实验结果证明了理论分析的准确性，显示了具有负载敏感度极低的特点且能够长期稳定运行，而且不含补偿电感、无磁饱和现象，同时获得高达92%的传输效率。