多逆变器同步输出控制设计及实现

王成亮，王 双，徐 妍，杨庆胜

（1.江苏方天电力技术有限公司，南京 211102；2.河海大学能源与电气学院，南京 210098；3.重庆大学自动化学院，重庆 400044）

随着无线电能传输WPT（wireless power transfer）系统得到市场更多的关注，耦合机构设计需要满足越来越多的功能和需求[1]。目前在单发射单接收的耦合机构方面有了很深入的研究，系统的输出效率、功率都与耦合机构密切相关[2],并且在这方面有了比较成熟的技术理论体系。然而在功率较大的用电设备或者负载过多的情况下，这种传输系统的传输效率会大大下降。而多发射单元的无线电能传输系统，使系统的灵活性得到提高，降低了系统的电流、电压应力，而且由于每一个发射单元都在传输电能，使得每个发射单元承受的电流更小，降低了系统设计难度与成本[3-4]。进行多逆变无线电能传输时，逆变器之间输出的相位差会造成发射线圈之间产生高频磁场，互相影响，导致磁场强度衰减，从而导致系统传输效率下降[5]。为了保证传输效率的最大化，应通过控制逆变器的驱动来改变控制器输出相位，从而达到多逆变器输出同步的效果。

本文对多发射单元无线电能传输系统结构、特性进行了研究，并分析了多逆变器输出之间相位差φ对系统效率、原边电流系统输出电压的影响，提出一种使逆变器实现同步输出的闭环控制方法。首先以磁耦合谐振式无线电能传输MCR-WPT（magneticallycoupled resonant wireless power transfer）系统为研究对象，给出多逆变MCR-WPT 系统模型及逆变器输出相位差对系统的具体影响；然后设计针对多逆变器输出的同步控制方案，主要包括检测电路设计与移相控制两部分；最后进行了实验验证。

1 多逆变MCR-WPT 系统

多逆变MCR-WPT 系统模型如图1 所示[6-7]，图中：US1和US2为两逆变器的输出电压，US为直流输入电压，US1=UScos（ωt），US2=UScos（ωt+φ），φ 为两个逆变器输出的相位差；C1、C2和C3分别为谐振网络的发射端和接收端补偿电容；L1、L2、L3分别为线圈的自感，R1、R2、R3为线圈的寄生电阻；RL为负载电阻；Uo为系统的输出电压；M12为L1和L2之间的互感，M13为L1和L3之间的互感，M23为L2和L3之间的互感。

图1 多逆变MCR-WPT 系统模型Fig.1 Model of MCR-WPT system

经过计算，得出输出电压Uo、输出功率Po、系统的效率η 分别为

式中：I3为输出电流；R 为线圈内阻，R=R1=R2；M 为原副边线圈互感，M=M13=M23；ω 为系统角频率。

将输入电压US1=UScos（ωt），US2=UScos（ωt+φ）代入式（1）～式（3），化简得

分析式（4）～式（6）得φ=0、US1=US2时，系统的输出电压、输出功率及系统效率最大。因此，需要进行控制，使两个逆变器保持同步输出[8-10]。

2 多逆变MCR-WPT 系统的同步控制

2.1 控制策略

本文对于对逆变器同步控制的主要思想是：当发射线圈和谐振电容调谐成功时，逆变器的负载属于纯阻性负载，因此逆变输出的电压与电流相位一致，因此，检测出流过两个线圈电流的相位即可知道两个逆变器输出的相位信息，而逆变器输出电压与驱动信号相位一致，所以可以通过检测到的电流信号改变驱动信号的相位，从而达到逆变器输出电压移相的效果。相位差检测的原理如图2 所示，图中：U1、U2为两路电压正弦信号；C 和D 分别为U1和U2经过过零比较后的方波信号；F 为两路方波信号的相位关系。测量两路信号之间相位差不仅需要保证两路信号的频率相同，而且要排除由于两路信号的幅值变化等因素对测量造成的影响[11]，应该尽量避开测量引起的相位误差。

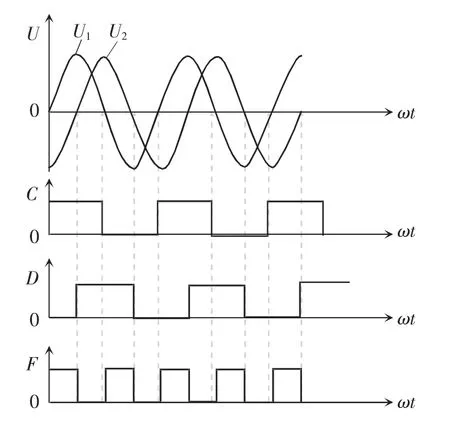
图2 相位差检测原理Fig.2 Principle of phase difference detection

图3 为同步控制框图，同步控制流程如图4 所示。已知流过两个发射线圈的电流为正弦信号，通过电流互感器可以将两路电流信号转换为电压信号采集，将采集的电压信号通过过零比较，得出两路方波信号，将方波信号进行分压得到能够送入控制器的电压信号，然后通过控制器2 读入两路方波信号，计算出信号的相位差。保持控制器1 的输出驱动信号不变，根据相位差信息对控制器2 输出的驱动信号进行移相，当检测到的相位差信息满足要求后，停止控制器2 输出的驱动信号的移相，此时两个发射线圈的电流相位基本相同，因此，两个逆变器的输出也达到了同步。

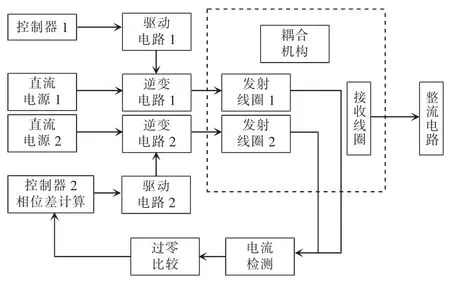
图3 同步控制框图Fig.3 Synchronization control block diagram

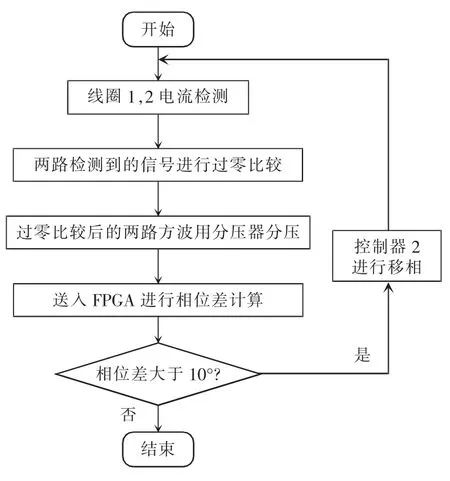
图4 同步控制流程Fig.4 Synchronous control flow

2.2 程序设计

本文主要用FPGA 作为控制器，相比于其他的控制器，FPGA 使用Verilog 或VHDL 进行编程，逻辑清晰，处理速度快，得到了广泛的应用。本文设计的多逆变器系统选择一块stm32f103 系列单片机和Cyclone IV 分别驱动两个逆变电路，由于不同控制器的时钟不同，产生的驱动信号并非同步，从而导致了逆变器输出不同步，因此，本文将一个stm32的驱动信号保持不变，Cyclone IV 的驱动信号通过移相达到同步输出的效果。

2.2.1 相位差测量

当电流检测电路和过零比较电路将发射线圈的电流处理为峰值为5 V 以下的方波信号时，就可以将两路信号传入FPGA 中进行相位差的测量，两路信号相位差如图5 所示。图中：U1、U2、U3为电压信号；以U1为电压标准信号，U2滞后于U1，U4反映U1和U2的相位关系，其高电平持续的时间t1可转换为U1、U2对应相位差φ1，φ1=360°·t1/T；U3超前于U1，U5反映U1和U3的相位关系，其高电平持续的时间t2可转换为U1、U3对应相位差φ2，φ2=360°·t2/T。

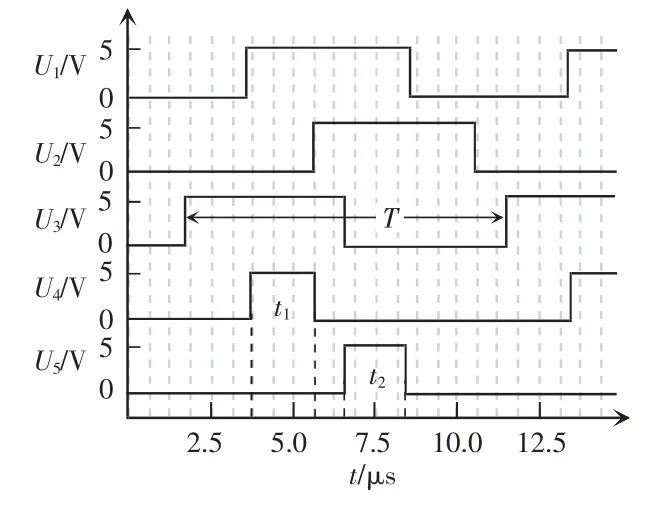
图5 两路信号相位差Fig.5 Phase difference of two signals

图6 为相位差检测流程，其中：CL 为超前滞后的判断，CL=0，则U1超前于U2；Q 为程序运行过程中相位差的计数器；XW 为最终相位差的数字量。

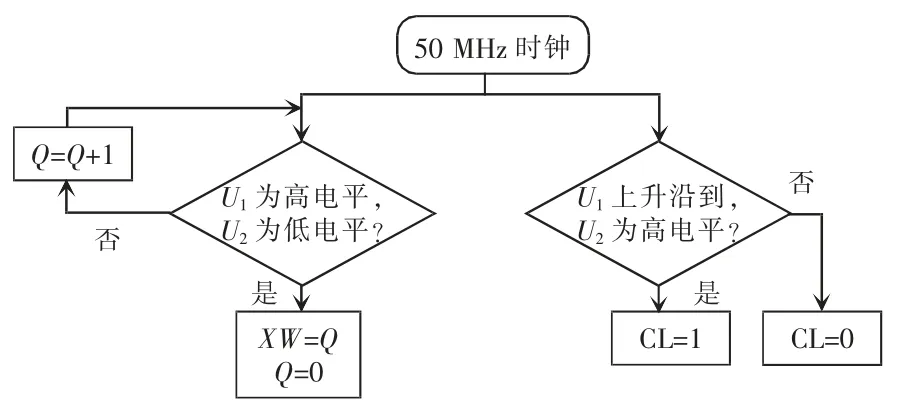
图6 相位差检测流程Fig.6 Phase difference detection flow chart

2.2.2 移相的实现及总控制流程

图7 是移相原理，主要通过计数延迟进行移相[12]，A 路波形为一个周期的基准波形，计数器计数500 次清零，计数低于250 时，输出为0，大于250 时，输出为1。令point 为计数器当前计数值，当需要进行向左移相时，可以设置为当计数值小于250-point 和大于500-point 时，输出为0，其余阶段输出为1，如图7 中B 路波形。当需要进行向右移相时，可以设置为当计数值小于point 和大于250+point 时，输出为1，其余阶段输出为0，如图7 中C路波形。通过改变point 值改变移相的角度。系统总控制流程和移相流程分别如图8、图9 所示。为了保证相位差检测的速度，系统用50 MHz 时钟进行相位差计算，得出相位差后就可以根据相位差是否大于10°给移相信号赋值，大于10°则移相信号为1，小于10°则移相信号为0。

图7 移相原理Fig.7 Phase shifting schematic diagram

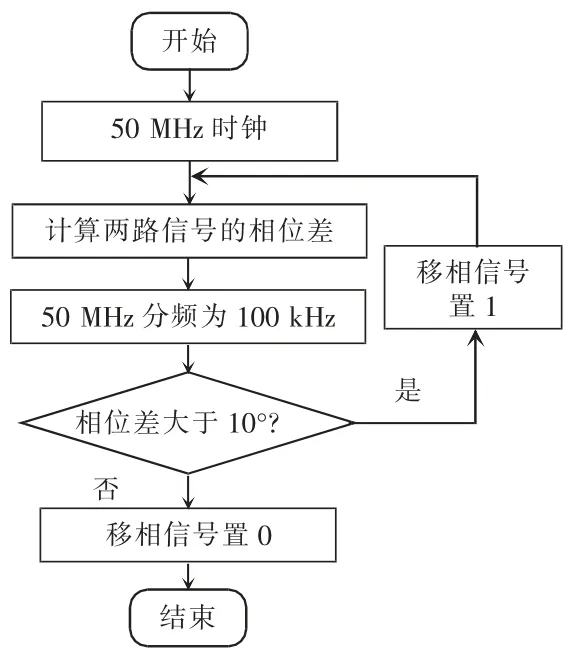
图8 总控制流程Fig.8 General control flow

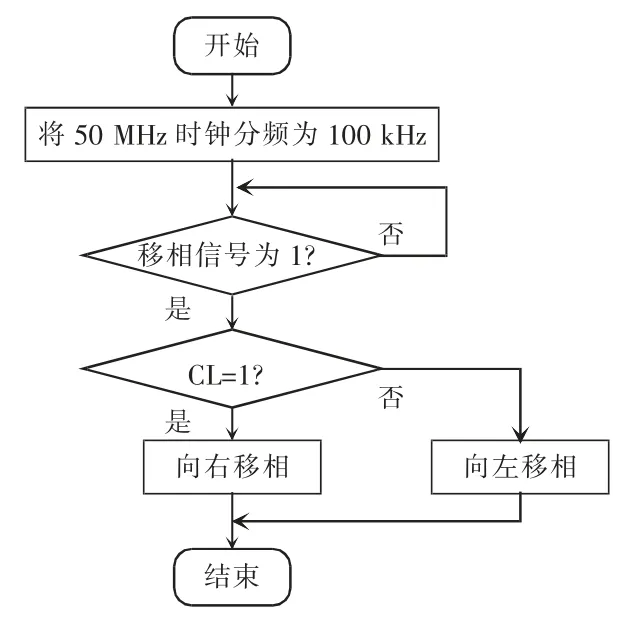
图9 移相流程Fig.9 Phase shifting flow

3 实验结果

根据图3 搭建的多逆变输出控制实验系统如图10 所示，其中包括控制器直流电源、逆变电路、谐振线圈和谐振电容、整流滤波电路、电流检测和过零比较电路。两个发射线圈与接收线圈的距离为5 cm。

图10 多逆变输出控制实验系统Fig.10 Experimental system of multi inverter output control

3.1 电流检测测试

当检测到电流信号后，需要对其进行整形以方便控制器能够准确地检测信号的相位差，整形即为过零比较。为了将信号传输到控制器中，还进行了电阻分压处理。示波器采集的过零比较结果如图11所示，波形1 为实际电流，波形2 为过零比较后经过降压处理的波形。可以看出，过零比较的效果较好，没有明显的相位滞后。

图11 过零比较结果Fig.11 Zero crossing comparison results

3.2 同步输出测试

由于同步输出控制为一个动态调节过程，所以随机选择时间点进行观察，示波器采集的同步输出控制如图12 所示，两者相位差很小，说明同步控制的效果较好。

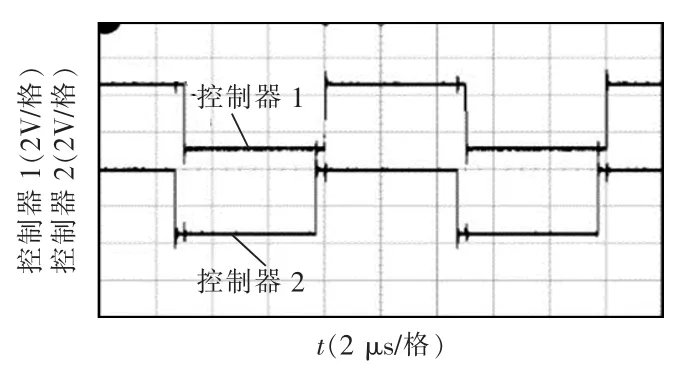
图12 同步输出控制Fig.12 Synchronous output control

3.3 效率分析

通过在搭建的实验系统上进行实验，输入直流电压为6 V，当逆变器之间的相位差改变时系统参数变化见表1。根据表1 可以绘出系统效率和输出电压与相位差的关系，分别如图13 和图14 所示，可以看出，随着相位差的增加，系统输出电压和整体效率都有所下降，和第1 节的结论相符合。由于输入的电压较小，而整流过程二极管存在管压降以及电路损耗等原因，效率比较低，当输入电压提升后，效率会逐渐上升。

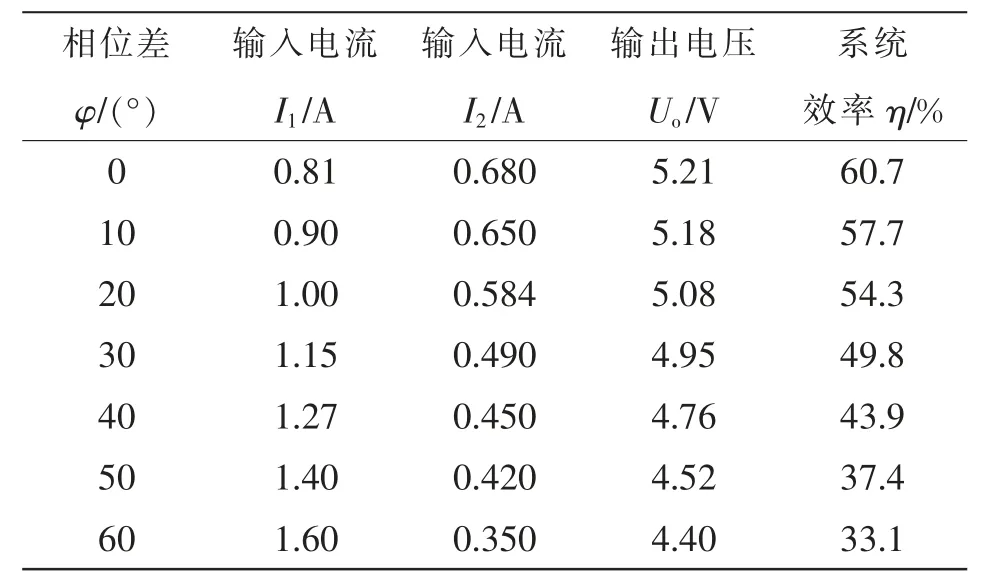
表1 相位差对系统参数的影响Tab.1 Effect of phase difference on system parameters

图13 系统效率随相位差的变化Fig.13 Variation of system efficiency with phase difference

图14 系统输出电压随相位差的变化Fig.14 Variation of system output voltage with phase difference

3.4 实验小结

经过实验发现，逆变器之间的相位差对系统影响很大，随着相位差增大，系统效率和输出电压都下降。当两个逆变器驱动信号来自不同的控制器时，由于时钟没有校准，逆变器输出相位不同，导致系统的输出电压、输入电流的变化，最终导致系统效率的变化。而加入同步输出控制后，虽然还存在一定的相位差，但保持在10°以内，因此系统效率有了很大提升。

4 结论

针对多逆变器的输出不同步造成多逆变无线电能传输系统输出的驱动信号不同步，最后影响整个系统电能传输效率问题，设计了一种闭环同步输出控制，利用系统运行在谐振频率下，逆变器输出电压与电流同相原理，用电流互感器采集逆变器输出电流（即线圈电流），串接电阻后，用电阻两端的电压信号代替逆变器输出电压，将其经过过零比较电路送入控制器，进行移相，形成闭环，达到输出同步的效果。后期将鉴于SS 型谐振补偿结构的局限性，考虑其他补偿；建立多逆变器之间的无线通信，增加系统的灵活性。主要展望如下：

（1）系统的效率提升问题，从实验结果来看，系统效率还有很大的提升空间，可从系统结构特点展开，研究决定系统传输效率的具体因素及其对系统的具体影响。

（2）采用的SS 型谐振补偿结构虽然有很多优点，但当系统谐振网络稍有变化时，使直流输入电流较大，器件承受的电流较大。因此，后续可寻找一种效果更佳的谐振拓扑网络进行实验。

（3）两个逆变器虽然是由独立的控制器提供的驱动信号，但在检测电路中还是将两个逆变器连接在一起，因此，可探讨通过无线通信方式，将发射端隔离开，形成两个完全独立的部分，将增加系统灵活性。