基于FCS-MPC 的柔性多状态电源开关高比例输配电模型研究
2022-08-05黄元生王宏伟
高 冲,黄元生,王宏伟
(华北电力大学经济与管理学院,北京 102206)
现代电子设备与电源具有不可分割的关系,对电源需求较高。与以往晶体管串联调整稳压电源存在较大差异,开关类稳压电源(简称开关电源)使用功率半导体构件作为开关,根据控制开关的占空比控制输出电压。随着时间的推进,开关电源凭借其体积小、重量轻、速度快、发热量较小和可靠性高的优势,慢慢取代了线性稳压电源[1]。柔性多状态电源开关FMPS(flexible multi-state power switch)在调控配电网时灵敏度极高,逐渐成为配电网科研领域关注的热点。FMPS 是和配电网里两条或多条馈线间相连的电力电子变流器,当配电网出现异常时,FMPS可以变换控制策略,完成非异常范围的连续供电,增强配电网的可靠性。
文献[2]提出多种分布式电源随机性的配电网优化运行方法,建立分布式电源的随机性模型,同时结合负荷的随机性及可控性,引入到配电网运行的优化模型中,采用粒子群优化算法求解得到考虑多种分布式电源随机性的配电网优化运行方法,实现配电网馈线间的负载平衡,但该方法的稳定性较差;文献[3]提出不平衡电网电压下柔性直流输电系统功率滑模补偿方法,构建VSC 换流器的数学模型,推导并建立不平衡电网电压下以系统二倍频功率为状态变量的控制方程,采用VSC-HVDC 功率滑模变结构补偿方法,抑制电流因素和电压因素引起的功率波动,提高了变工况状态下系统的动态响应性能,以保证配电网的稳定性,但该方法应用范围有限。
为此,本文构建了基于FCS-MPC 的柔性多状态电源开关高比例输配电模型,对柔性多状态电源开关的建模分析和控制策略进行了深度探讨[4]。
1 基于FCS-MPC 的柔性多状态电源电源开关高比例输配电模型
1.1 FCS-MPC 控制策略
使用FCS-MPC 控制策略,构建基于FCS-MPC的柔性多状态电源开关的高比例输配电模型[5]。当柔性多状态电源开关工作时,一般情况下,直流稳压控制VdcP 模式中存在柔性多状态电源开关一端,恒有功和无功功率控制PQ 模式中存在柔性多状态电源开关两端。控制策略通常使用比例积分控制器PI(proportional and integral)双闭环控制方法,电流控制环属于内环,功率与电压的控制属于外环,这种情况下柔性多状态电源开关需要12 个PI 控制环节,导致调整控制参数时存在一定难度,并且在dq 旋转坐标系里的锁相与解耦控制也存在一定难度[6]。本文通过离散数学模型实现控制,根据控制函数选取最佳开关量,操作简单,便于实现,能够降低PI 参数调整难度,响应效率较高[7]。
综合应用需求,本文提出FCS-MPC 的控制策略,该策略中包含了PQ 模式控制策略、VdcP 模式控制策略和恒电压和频率控制Vacf 模式控制策略。
1.1.1 PQ 模式控制策略
控制柔性多状态电源开关高比例输配电的离散数学模型可表示为

式中:Vfj(h)为柔性多状态电源开关端口输出电压;ts为采样时间;L 为配电网侧滤波电感;Vsj(h)为配电网侧电压的参考预测值;h 为周期向量。
通过二阶拉格朗日外推法运算配电网侧电压的参考预测值,预测方法是

PQ 模式中,必须控制柔性多状态电源开关端口输出的有功、无功功率。功率控制函数f1为
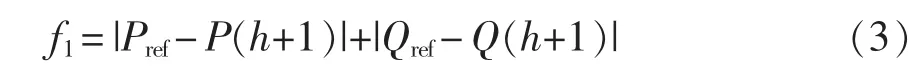
式中:Pref为有功功率参考值;Qref为无功功率参考值;P(h+1)和Q(h+1)分别为开关一侧的端口所流出的有功功率和无功功率真实值。
此处控制函数里的变量均为功率,存在一样的控制属性,所以控制权重不存在差异[8]。
1.1.2 VdcP 模式控制策略
顾及到柔性多状态电源开关高比例输配电时,直流侧电容电压稳定是以有功支撑为宗旨,那么直流侧电压的控制能够以调整有功功率的形式完成[9]。功率控制方法为

式中:idco为直流侧流向剩余端口的电流和;P*为柔性多状态电源开关端口有功功率参考值;ki和kp分别为PI 调节器的积分与比例系数;和vdc分别为直流侧参考电压与采样电压。
1.1.3 Vacf 模式控制策略
上文分析了配电网稳定工作时FMPS 常用的两类工作形式和解决方案。若馈线由于异常情况失电,但必须保障核心程序继续供电,则柔性多状态电源开关端口的控制对象输出恒定频率、幅值的交流电压,运行于Vacf 模式[10]。
通过dq 坐标变换获取柔性多状态电源开关在非动态坐标系中的数学模型,即
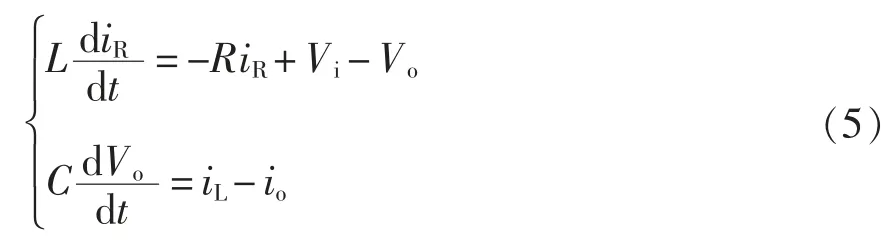
式中:R 为等效电阻;io为输出电流;iL为电感电流;C 为输出滤波电容;Vo为输出电压;Vi为输入电压[11]。
最终获取控制柔性多状态电源开关高比例输配电时的状态空间方程为

式中,柔性多状态电源开关高比例输配电时的状态向量y=[iL,Vo]T,B 与C1、C2均为状态向量。
把式(6)离散化后获取离散化的状态空间方程为

通过离散状态空间方程,便能够获取第h+1 周期的交流电压预测值vo(h+1)[12]。
按照柔性多状态电源开关高比例输配电时,恒压、恒频的电压输出条件,柔性多状态电源开关端口输出交流电压的参考值为


按照交流输出电压的约束条件构建约束函数f2,即

1.2 柔性多状态电源开关模型
柔性多状态电源开关包含了多个对称的电压源型变流器[14-15]VSC(voltage source converter),其原理如图1 所示。
单纯组:男10例,女9例;年龄21-67岁,均值(41.65±3.25)岁;病程最短1个月,最长5年,平均(3.12±0.52)年。

图1 柔性多状态电源开关的原理Fig.1 Principle of flexible multi-state power switch
在柔性多状态电源开关中使用LCL 滤波,当柔性多状态电源开关高比例输配电时,L1为变流器侧滤波电感,R1为内阻与线路等效电阻,L2为电网侧滤波电感,R2为L2的等效电阻,C 和Cdc分别为滤波电容与直流侧稳压电容,vo为变流器输出电压,vs为电网电压,i1和i2分别为经过滤波电感L1和L2的电流;i01和i02为变流器直流侧电流。
若柔性多状态电源开关的功率开关构件不存在异常,则三相桥臂开关信号Wθ为

式中:vdc为直流侧电压;na1、nb1、nc1为柔性多状态电源开关变流器VSC 里的节点向量,表示为
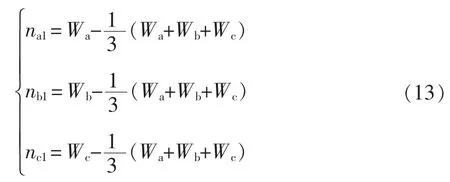
式中,Wa、Wb和Wc为三相桥臂开关信号。
柔性多状态电源开关变流器VSC 中每个节点电压的计算方法为

式中:vCθ为滤波电容电压;vθ为变流器输出θ 相的电压;i1θ和i2θ为三相桥臂电流。
直流侧电压动态方程为

不分析滤波电容C 的干扰,以dq 坐标系为分析环境,则柔性多状态电源开关模型为

式中:R=R1+R2;L=L1+L2;ϖ1为柔性多状态电 源开关高比例输配电时的角速度;vd和vq分别为d、q 轴电压分量;id1和iq1分别为VSC 电流的d、q 轴分量;nd1和nq1分别为VSC 开关信号的d、q 轴分量。
直流侧电压变动方程为

式中:id2和iq2分别为VSC 电流的d、q 轴分量;nd2和nq2分别为VSC 开关信号的d、q 轴分量。
不计柔性多状态电源开关高比例输配电时的线路损失与开关损失,有功功率P 与无功功率Q分别为

因为在配电网电压高比例输配电定向的前提下vq=0,故

最后,根据第1.1 节与1.2 节可以得出,基于FCSMPC 的柔性多状态电源开关高比例输配电模型为
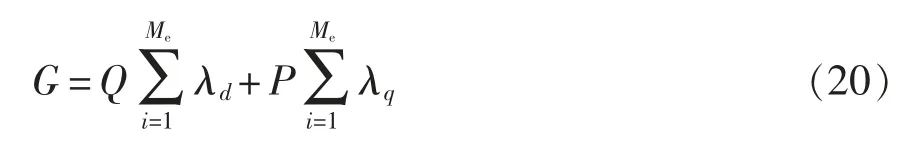
式中:Me为进入状态i 的转移数;λd和λq分别为线路损失率和开关损失率。
2 实验分析
为了测试本文模型性能,以柔性多状态电源开关为例进行仿真实验,模拟双端配电网络,可以调控不同电压等级、电网频率、电压和相位。首先设定从500 kV 系统回送给220 kV 系统,在配电网高比例输配电稳态运行状态下,使用本文模型对柔性多状态电源开关实施控制。在设置三相不平衡运行的环境,使用本文模型进行有效控制,实验参数设定见表1。
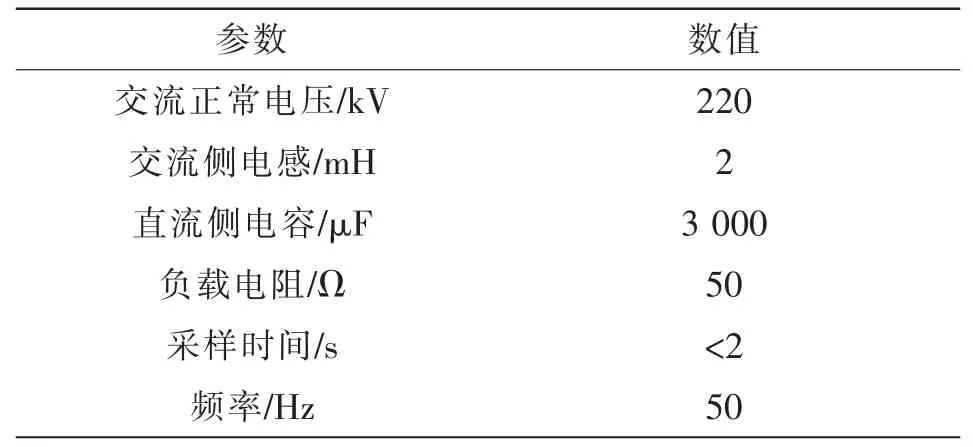
表1 实验参数设定Tab.1 Setting of experimental parameters
2.1 配电网稳态运行控制效果
为验证基于FCS-MPC 的柔性多状态电源开关高比例输配电模型的综合有效性,需要进行实验测试。功率响应波形越平稳、调整越迅速,表示研究模型的配电网中馈线功率调节性能越好;直流侧电压变化越稳定,表示研究模型的稳态运行效果越好。当配电网稳态工作时,对研究模型的控制结果进行测试,假设柔性多状态电源开关具有3 个端口,端口1 与端口2 的运行处于PQ 模式,并在1.31 s 时调节PQ 端口的输出功率,检测研究模型跟踪有功功率的变化情况,端口3 的运行属于VdcP 模式。初始背景下,有功功率参考值P=0.84 p.u.,无功功率参考值Q=0。图2 是PQ 端口的输出响应波形。
分析图2(a)可知,当h=1.20 s 时,研究模型的有功功率P=0.84 p.u.,与参考值一致,无功功率参考值Q=0;当h=1.31 s 时,P 减小为0.34 p.u.,Q 减小为-0.8 p.u.。由此可知,PQ 端口的初始有功功率与标准值相同,输出功率能够高效跟踪有功功率变化并进行调整,且输出电压、电流响应不存在波动,可以证明研究模型的配电网中馈线功率调节性能较好;分析图2(b)可知,当每个端口功率存在变动时,研究模型的直流侧电压没有产生变化,证明研究模型可以保证直流侧电压不出现异常,维持装置平稳工作,实现稳态运行。

图2 稳态运行控制响应波形Fig.2 Response waveforms under steady-state operation control
当配电网稳态运行时,本文模型可以按照变流器间每个相连的馈线负载率,变换每条馈线的功率。如图3 所示,此处负载率描述的是本文模型在电网中得到的功率和线路容量最大值之比,馈线的负载率越统一,表示模型的运行状态越稳定。
由图3(a)可知,在本文模型控制下,初始条件中馈线1、2 和3 的有功负载率依次是81%、31%和11%,当h=1.20 s 时,研究模型开始控制3 条馈线,经过功率变换,把馈线2 与3 中的有功功率依次变换至馈线1,减轻馈线1 的负载情况,完成3 个馈线的负载平衡,增强了配电网的可靠性和稳定性,实现负载平衡。由图3(b)可知,研究模型将每条馈线中的无功需求进行补偿,当h=1.20 s,有功功率出现变化时,实现3 个馈线无功功率的统一处理,以保障配电网的正常运行。

图3 馈线均衡实验结果Fig.3 Results of feeder equalization experiment
2.2 配电网三相不平衡时的控制效果
假定柔性多状态电源开关两端电网中,VSC1是三相平衡电网,VSC2初始状态属于三相电压均衡。
实验设定两端配电网相位差为35°,当h=0.07 s时,柔性多状态电源开关开始运行,此时,电网接收VSC2传输的无功功率是3 kW,不存在有功功率;当h=0.09 s 时,VSC2侧电网接收的VSC1侧电网有功功率是8 kW;当h=1.16 s 时,把VSC1配电网里某相电压的幅值从312 V 变换为283 V;当h=1.23 s时,把VSC1配电网里该相电压的幅值从283 V 变换为312 V,用于描述三相电压非平衡状态。将本文模型应用于该情境中,如果一端配电网电压参数出现变动,引起两侧配电网传输的电网电压也发生变化,则会影响配电网平稳运行,配电网三相不平衡时本文模型控制效果如图4 所示。
分析图4 可知,当一端配电网电压参数出现变动时,本文研究模型能够快速保证两侧配电网传输的电网电压一致,且直流侧电压vdc平稳运行,由此可以证明研究模型能够保障配电网的正常运行。
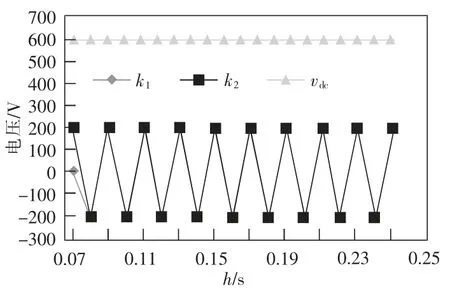
图4 配电网三相不平衡时本文模型控制效果Fig.4 Control effect of the proposed model in the case of three-phase unbalanced distribution network
3 结论
为了保证配电网供电系统安全、持续地供电服务,本文针对柔性多状态电源开关的数学模型进行设计,构建了一种柔性多状态电源开关高比例输配电模型,将其应用于高比例输配电实验中得出如下结论。
(1)本文模型控制下,PQ 端口的输出功率可高效跟踪有功功率进行调整,且输出电压、电流响应不存在波动。
(2)当每个端口功率存在变动时,本文模型可以保证直流侧电压不出现异常,维持装置平稳工作。
(3)本文模型可完成3 个馈线的负载平衡,增强配电网的可靠性和稳定性。
(4)本文模型能够快速保证两侧配电网传输的电网电压一致,且直流侧电压vdc平稳运行,以保障配电网正常运行。
