提升运行工况适应性的PSS 相位和增益参数协同整定方法
2022-08-05李登峰刘育明杨旼才徐瑞林李昭炯
李登峰,刘育明,杨旼才,徐瑞林,余 霞,李昭炯
(1.国网重庆市电力公司电力科学研究院,重庆 401123;2.国网重庆市电力公司,重庆 400014)
我国现代电力系统互联规模的日益扩大,以及高放大倍数快速励磁系统的大规模应用,增加了系统出现低频振荡的风险。电力系统稳定器PSS(power system stabilizer)作为一种励磁附加控制,对提升电网低频振荡抑制能力、改善电力系统稳定性作用显著。我国电力行业近二十年的大规模应用实践表明:到目前为止,PSS 仍是提升系统阻尼水平、抑制低频振荡最经济成熟的首选措施[1-3]。
目前,各网省公司PSS 参数整定普遍采用现场试验的方法。由于试验工况和条件的限制,试验过程无法全面模拟各种可能出现的运行工况,通常只能在少数1~2 个工况下进行,整定得到的PSS 参数也只能保证特定工况下的最优。当系统运行工况发生变化时,PSS 参数的相位补偿效果将难以满足当前工况下的性能要求,适应性较差[4-6]。
PSS 需要整定的参数主要分为相位参数和增益参数两类。根据力矩分析法,PSS 作用强弱不仅与PSS 经励磁调节器产生的电磁力矩ΔMPSS的相位有关,也与其幅值有关。常规PSS 参数整定的具体做法是:基于相位补偿原理,以最佳相位补偿为目标优化获得一组PSS 相位参数,然后基于此相位参数通过临界增益试验按临界增益的1/5~1/3 取值得到PSS 的增益参数[7]。
尽管PSS 增益参数与其补偿相位大小无关,但相位参数对PSS 增益裕度有直接影响,进而影响增益参数的取值。研究表明:传统基于最佳相位补偿法整定得到的增益参数,通常并不能保证PSS 具有最佳阻尼效果,有时候适当牺牲一点相角补偿,可以大大提升PSS 增益裕度,进而整体提高阻尼的效果[8]。因此,传统整定方法通常只强调相位补偿的要求,对相位参数和增益参数分步进行整定,忽略了相频特性和幅频特性之间的协调性对PSS 阻尼效果的共同影响。事实上,PSS 的阻尼效果由幅频特性和相频特性共同决定[9]。
本文重点分析相位参数对PSS 临界增益和阻尼力矩分量的影响,以及运行工况对PSS 参数整定的影响,提出兼顾运行工况适应性的PSS 相位和增益参数协同整定方法。通过构建以PSS 阻尼力矩分量最大为目标,以满足多种运行工况相位补偿要求为约束条件的最优化模型,实现对PSS 相位参数和增益参数的协同整定,以增强PSS 适应多种运行工况的性能和全频段的阻尼效果。
1 PSS 临界增益
1.1 临界增益估算原理
实际上,包含同步机、励磁系统和PSS 的闭环控制系统具有高阶、非线性的复杂特点,提高PSS增益尽管可以增加某些机电振荡模式的阻尼,但过大的PSS 增益,也可能导致系统出现不稳定的振荡现象,因此,PSS 实际存在一个最大增益,即为临界增益[10]。目前“自并励静止励磁+PSS2A/2B 电力系统稳定器”控制模式在我国发电机组中应用最为广泛,因此下面均以该控制模式为例进行说明。
自并励励磁系统及PSS 相频特性如图1 所示。以-ΔPe为基准轴,通常自并励励磁系统的无补偿相位和PSS 的补偿相位在高频段(3 Hz 以上)均呈现单调下降的特性,频率越高,两者相位之和即励磁系统有补偿相位将越小(滞后-ΔPe轴的角度越大),可能穿越-180°。根据控制系统稳定性原理,如果在穿越点处对应增益为0 dB,则励磁-PSS 控制回路增益达到临界值,将出现高频振荡失稳现象[11]。依据此原理,在任意一组PSS 相位参数已知的前提下,可实现对PSS 临界增益的同步估算。
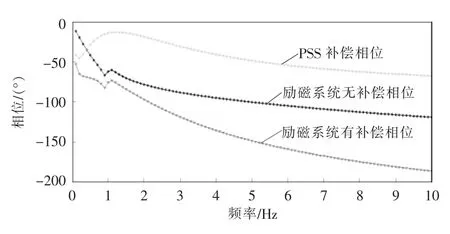
图1 自并励励磁系统及PSS 相频特性Fig.1 Phase-frequency characteristics of self-excited excitation system and PSS
1.2 相位参数对临界增益的影响
基于单机无穷大系统的Heffron-Philips 模型[12],仿真计算得到励磁-PSS 回路的幅频和相频特性,波特图如图2 所示。励磁调节器采用PSASP 电力系统分析综合程序12 型模型,其传递函数GE(s)为
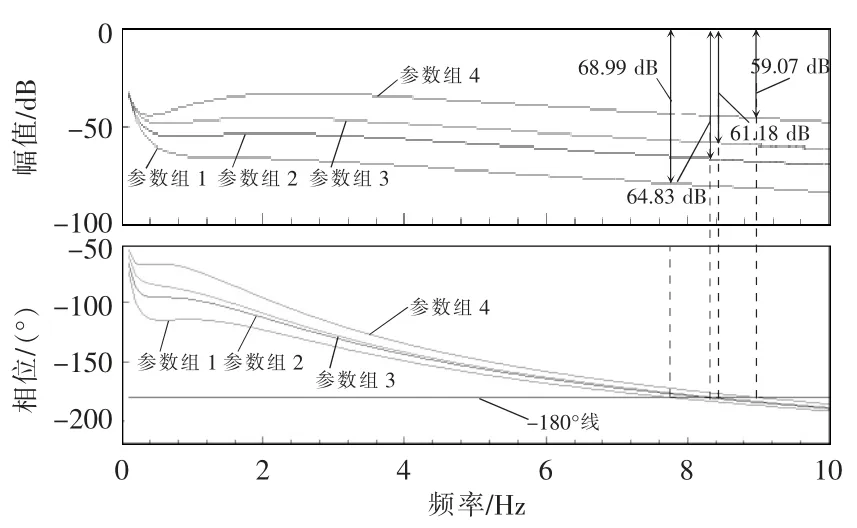
图2 励磁-PSS 回路的波特图Fig.2 Bode diagram of excitation-PSS loop

PSS 采用如图3 所示的2A 模型,其中:Tw1=Tw2=Tw3=T7=7 s,Tw4=0 s,T8=0.6 s,T9=0.12 s,M=5,N=1,KS3=1,KW=1;相位参数T1~T4、T11、T12取值以及基于上述临界增益估算方法求得的4 组参数对应的PSS 增益度Kg和临界增益Kr如表1 所示。

图3 PSS 2A 传递函数模型Fig.3 PSS 2A transfer function model
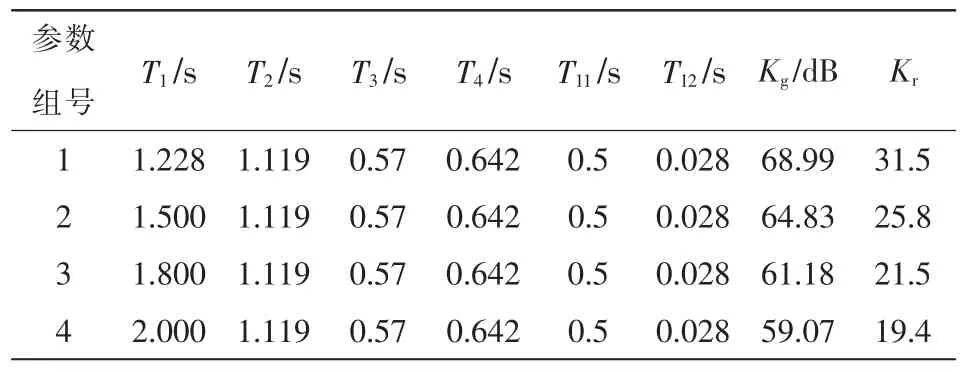
表1 PSS 超前滞后环节的4 组相位参数Tab.1 Four groups of phase parameters of PSS lead lag link
从表1 和图2 可以看出:在其他参数不变的情况下,随着T1的增加,励磁-PSS 回路的增益裕度Kg减小,临界增益Kr也随之减小;反之,随着T1的减小,励磁-PSS 回路的增益裕度Kg增加,临界增益Kr也得到提高。由于T1、T3和T11均为超前环节相位参数,因此适当减小T1或T3或T11,PSS 的补偿相位会随之减小,即相当于适当牺牲了一定的PSS补偿相位,但反而可以提高回路的增益裕度,进而提升PSS 的临界增益。
1.3 相位参数对PSS 阻尼力矩分量的影响
PSS 经励磁回路产生的附加力矩的阻尼分量,简称PSS 阻尼力矩分量ΔMPSS,计算公式为
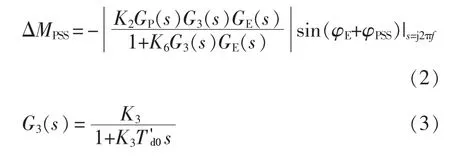
式中:GP(s)为PSS 传递函数;G3(s)为单机无穷大系统的Heffron-Philips 模型[12]中励磁电压变化量相对于暂态电势的相频特性;K2、K3、K6为Heffron-Philips模型中的K 系数;为发电机直轴开路瞬变时间常数;φE和φPSS分别为励磁系统无补偿相位和PSS的补偿相位;f 为低频振荡频率。
由式(2)可以看出:PSS 阻尼力矩分量不仅与PSS补偿相位相关,还与其幅值强相关;PSS 相位参数不仅影响其阻尼力矩分量的相位,还影响其幅值。
图4 给出了表1 中4 组相位参数下,增益参数KS1取不同临界增益时ΔMPSS和A=-sin(φE+φPSS)随频率(0.1~2.0 Hz)的变化曲线。

图4 4 组相位参数下的ΔMPSS 和A 的曲线Fig.4 Curves of ΔMPSS and A values under four groups of phase parameters
传统的PSS 参数整定试验方法在进行参数整定时,优化目标通常考虑为φE+φPSS在0.1~2.0 Hz范围内各频率点处尽量接近-90°,即在各频率点处A 值尽量接近1。但图4 显示,在4 组参数中,A 值整体最接近1 的是参数组4,ΔMPSS整体最大的却是参数组1,即4 组参数中,参数组4 具有最佳的相位补偿效果,但其阻尼效果却不及参数组1。主要原因在于,参数组1 通过牺牲一部分相位补偿度来显著提高临界增益,进而整体提升了PSS 的阻尼力矩分量。
2 运行工况对励磁系统无补偿相频特性的影响
2.1 励磁系统无补偿相频特性的计算
根据Heffron-Philips 模型,可推导出理论励磁系统无补偿相频特性GEX(s),以下简称为励磁系统无补偿相频特性,即

Heffron-Philips 模型中K 系数K1~K6的计算公式[12]为

式中:xd、xq、为同步发电机阻抗参数;xs为发电机与系统之间的等值联系电抗;u0为单机无穷大系统的等值母线电压初值,均可由PMU 运行数据按文献[13-14]的方法辨识得到;ut0、utd0、utq0、iq0、EQ0、δ0为中间变量,可由发电机有功功率P、无功功率Q、机端电压Vt等运行参数,通过同步发电机基本方程求解得到。可见,K1、K2、K4~K6与发电机运行参数以及电网联系电抗密切相关。
2.2 工况运行参数对励磁无补偿相频特性的影响
新版《导则》[15]规定,PSS 参数整定试验时机组有功功率应大于额定有功功率的60%。依次分析了P、Q、Vt及xs等发电机工况运行参数对励磁系统无补偿相频特性的影响,得到如图5 所示的不同运行工况运行参数下励磁系统无补偿相频特性曲线。
由图5 可知,除了发电机机端电压外,有功功率、无功功率以及等值联系电抗3 个工况参数对励磁系统无补偿相频特性影响较为明显。在其他条件不变的情况下,励磁系统无补偿相位(滞后相位)随有功功率的增加而增加、随无功功率的增加而减少、随等值联系电抗的增加而减少。

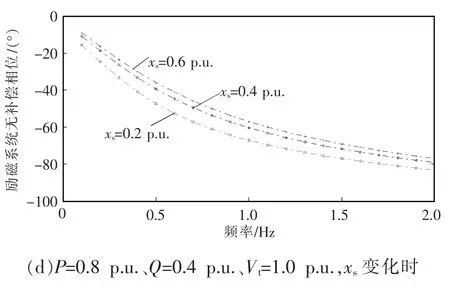
图5 不同运行工况运行参数下励磁系统无补偿相频特性曲线Fig.5 Non-compensation phase-frequency characteristic curves of excitation system under parameters of different operation conditions
3 PSS 相位和增益参数协同整定方法
3.1 PSS 阻尼力矩分量最大化目标函数
由PSS 相位参数对其阻尼力矩影响分析可知,满足相位补偿目标的PSS 最优参数并不一定能保证PSS 阻尼力矩分量ΔMPSS在0.1~2.0 Hz 频段内取得整体最大值。因此,为保证PSS 在整个低频振荡频率范围内能够具有最佳阻尼效果,构建以PSS阻尼力矩分量最大为目标的参数整定优化模型,目标函数为

由式(2)中ΔMPSS的表达式可知,目标J 同时是PSS 相位参数和增益参数的函数,即PSS 阻尼力矩分量既与PSS 相频特性有关,也与幅频特性有关。因此上述目标函数可以很好地兼顾两者之间的协调,使得PSS 的阻尼效果最佳。
3.2 兼顾运行工况适应性的相位补偿约束
根据新版《导则》要求:①通过调整PSS 相位补偿,使PSS 附加力矩在0.1~0.3 Hz(不含0.3 Hz)频段超前Δω 轴不应大于30°,在0.3~2.0 Hz 频率的附加力矩应在超前Δω 轴20°至滞后Δω 轴45°之间;②计算励磁系统无补偿相频特性宜分别在对应最大滞后角工况(P=1.0 p.u.、Q=0 p.u.、Vt=1.0 p.u.、xs=0.2 p.u.)和最小滞后角工况(P=0.5 p.u.、Q=0.5 p.u.、Vt=1.0 p.u.、xs=0.4 p.u.)2 种工况下进行计算;③PSS增益可取临界增益的1/5~1/3。
现有PSS 参数整定的优化模型中通常只考虑了满足试验工况下的相位补偿要求,而其他运行工况的相位能否满足补偿要求未作考虑,因此参数适应性难以保证。由第2.2 节的分析可知,试验工况对应的励磁系统滞后相位介于最小滞后角工况和最大滞后角工况之间。因此,若PSS 参数同时满足这2 种工况下的相位补偿要求时,将大幅提升PSS 参数相位补偿的工况适应性。基于此,式(6)需满足的约束条件为
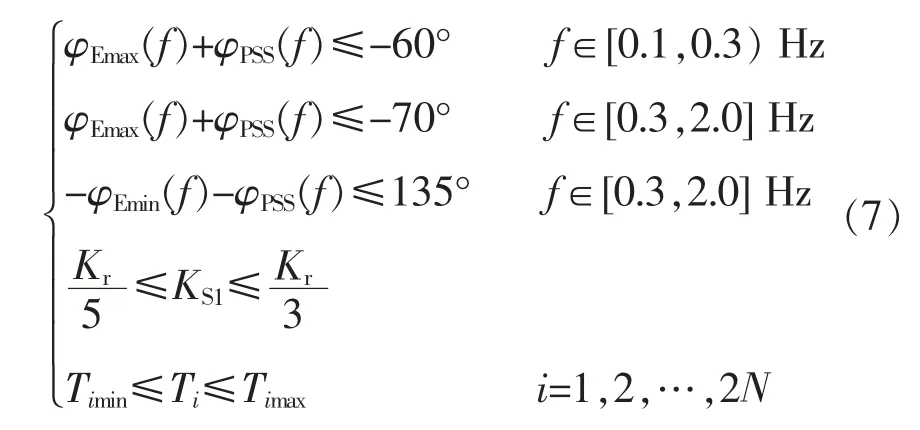
式中:Timax、Timin分别为相位参数Ti的上、下限;N 为相位补偿环节的个数,通常取3;由于励磁系统无补偿相位为滞后角(小于0°),因此最小滞后角工况对应的励磁系统无补偿相位(含负号)大于最大滞后角工况,可分别用φEmax、φEmin表示。
3.3 模型求解算法
粒子群优化PSO(particle swarm optimization)算法是一种广泛应用于电力系统优化问题研究的仿生随机搜索优化算法[16-17],具有无需二进制编码、算法规则简单、可调参数少、收敛速度快、目标函数容易实现、对优化目标灵敏性较高等优势[18-19]。以式(6)、式(7)联立得到优化数学模型,采用PSO 算法进行求解,可同时求得满足目标的最佳PSS 相位和增益参数。
4 算例分析
为了分析验证所提参数整定方法,采用某电网公司实际系统中汽轮发电机G 为算例,基于PSASP电力系统综合分析程序进行仿真验证。该机组额定容量Sn=412 MV·A、额定有功功率Pn=350 MW、转子惯性时间常数TJ=7.94 s、=11.95 s、直轴同步电抗xd=2.227 4 p.u.、交轴同步电抗xq=2.205 5 p.u.,采用12 型AVR 模型和4 型PSS 模型。调取该电网公司2019 年某次事故扰动情况下的PMU 数据对发电机G 进行单机无穷大等值系统参数辨识,得到机组工况运行参数分别为:P=0.82 p.u.、Q=0.18 p.u.、Vt=0.99 p.u.、xs=0.18 p.u.,进而计算得到其励磁系统无补偿相频特性。基于此,分别采用传统方法和本文所提方法进行PSS 参数整定,参数整定结果见表2。
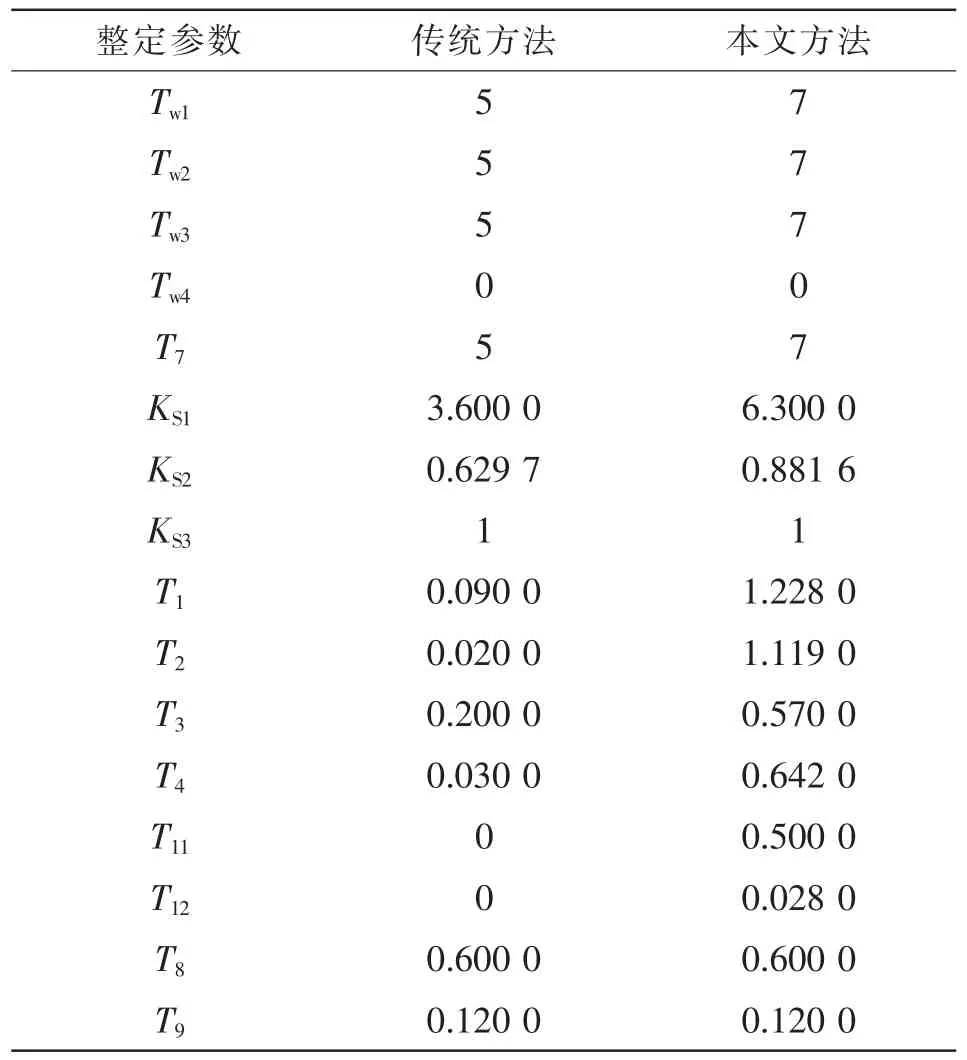
表2 发电机G 的PSS 参数整定结果Tab.2 PSS parameter setting result of generator G
传统方法和本文方法所得2 组参数下励磁-PSS 回路的波特图如图6 所示。两组参数的A 值曲线及PSS 阻尼力矩分量曲线如图7 所示。

图6 2 种方法所得PSS 参数下励磁-PSS 回路的波特图Fig.6 Bode diagram of excitation-PSS loop under PSS parameters obtained by two methods
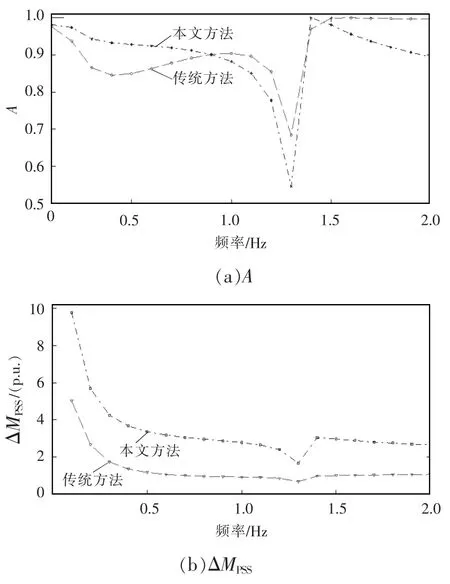
图7 2 种方法所得PSS 参数下的A 和ΔMPSS 曲线Fig.7 Curves of A and ΔMPSS values under PSS parameters obtained by two methods
由图6 可知,本文方法所得参数尽管在0.1~2 Hz 的相位补偿效果不及传统方法,但励磁-PSS回路增益裕度比传统方法对应的增益裕度高2.99 dB,PSS 临界增益也比传统方法高出22%。若2 种方法下PSS 增益KS1均按各自临界增益Kr的1/5 取值,则本文方法的PSS 增益应只比传统方法高出22%,但表2 显示采用本文方法后PSS 增益比传统方法高出了75%。主要原因在于传统试验方法在进行临界增益试验时并未到达真正的临界点,导致整定的PSS 增益往往比较偏保守。
进一步结合图7 可知,传统方法的A 值整体接近1 的程度(用各频率点A 值与1 之差的平方和大小进行表征)明显大于本文方法,但其PSS 提供的阻尼力矩分量ΔMPSS却远低于本文方法,这恰好显示了以PSS 阻尼力矩分量最大化作为优化目标的差别。
为进一步验证本文所提方法的有效性,图8 对比了机端电压5%阶跃和机组并网线路N-1 两种扰动情况下,传统方法和本文方法PSS 参数的阻尼效果。从有功功率振荡曲线明显可以看出,2 种扰动情况下,本文方法PSS 参数对应的有功功率曲线收敛性明显优于传统方法。
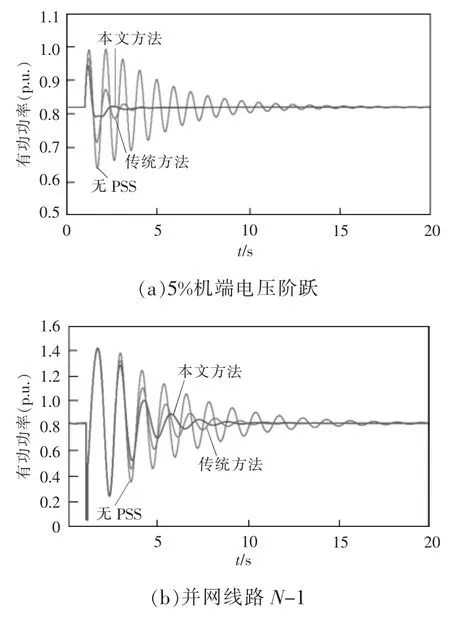
图8 传统方法和本文方法下PSS 参数的阻尼效果比较Fig.8 Comparison of damping effect of PSS parameters between traditional and proposed methods
采用本文方法整定的PSS 参数,计算得到最大、最小滞后角工况下励磁有补偿相频特性如图9 所示。可以看出,2 种工况下的有功补偿相频特性均满足新版《导则》中相位补偿的要求。在最大、最小滞后角工况下进行5%机端电压阶跃扰动时,投入本文方法得到的PSS 参数后有功功率仿真曲线如图10 所示。可以看出,有功功率的振荡较无PSS 情况下均得到了明显抑制。因此,也验证了本文方法所得PSS 参数能够很好地兼顾运行工况的适应性。

图9 最大、最小滞后角工况的励磁有补偿相频特性Fig.9 Phase-frequency characteristics of excitation with compensation under conditions of maximum and minimum lagging angles

图10 本文方法所得PSS 参数的工况适应性校验结果Fig.10 Adaptability check results of PSS parameters obtained by proposed method
5 结论
本文提出了提升运行工况适应性的PSS 相位和增益参数协同整定方法。该方法计及了PSS 幅频和相频特性之间的协调性,通过构建以PSS 阻尼力矩分量最大化为目标,计及多种运行工况相位补偿约束的最优化模型,可同步实现对PSS 相位参数和增益参数协调整定,以增强PSS 参数的运行工况适应性和低频振荡抑制效果。
以某电网公司实际系统中某汽轮发电机为例进行仿真验证,对比分析了机端电压阶跃、发电机并网线路N-1 故障扰动下本文方法和传统方法的有功功率振荡仿真曲线,验证了本文所提方法的有效性和优越性。该方法在无需对PSS 装置进行改造升级的情况下,可以进一步提升PSS 的低频振荡抑制能力和参数适应性,具有较强的工程实用性。
