再论联邦滤波在组合导航中的应用可行性

严恭敏，戴晨杰，刘 璠

(西北工业大学自动化学院，西安 710072)

0 引言

标准Kalman滤波的计算量与状态维数的3次方成正比，计算量因状态维数的增加而急剧变大。一个复杂的大系统往往包含众多的状态变量，但大系统通常可以分解成若干子系统，并且在子系统中可能还存在一个关键的公共参考系统。针对这类大系统，可以设计一个高维的综合滤波器，包含所有状态变量，再进行Kalman滤波，这一处理方式通常称为集中式滤波(Centralized Kalman Filter, CKF)；也可以采取所谓的联邦滤波(Federated Kalman Filter, FKF)方法进行分散降阶处理，有利于降低各子系统的计算量，还便于各子系统的故障诊断和隔离，避免有故障的子系统影响整个滤波器，从而提高总体性能。在联邦滤波中，如果所有子滤波器的状态均为公共状态，则全局状态融合精度与集中滤波器精度相同，结果均是最优的；但是当某些滤波器存在私有状态时，联邦滤波的精度一般低于集中滤波，这时联邦滤波是一种次优滤波算法。联邦滤波最早由N.A.Carlson提出，他在提出联邦滤波时曾声称联邦滤波器已被美国空军的容错导航系统“公共卡尔曼滤波器”计划选为基本算法，但从目前组合导航系统的发展情况看，历经30余年实践该算法并没有明显的优势，未获得广泛的实际应用。

对于所有子滤波器的状态均为公共状态的联邦滤波，不具备减小计算量的优势，分散为几个滤波器后反而增加了计算量，这种联邦滤波完全可以被序贯滤波所取代，序贯滤波同样易于量测故障诊断和隔离。提出联邦滤波的初衷和优势应当在于存在大量私有状态的系统。论文在分析传统联邦滤波基本原理的基础上，首先通过一个简单随机系统仿真例子，验证了联邦滤波估计结果的不合理性。显然，若对简单系统不可行，面对更加复杂的系统将更难获得好的估计效果。接着，以典型的速度+姿态传递对准为例，通过仿真实验验证了联邦滤波的状态估计效果不好，与集中滤波相比联邦次优滤波的误差太大，不能满足应用需求。最后，给出研究总结：已有文献普遍认为联邦滤波是一种有效的状态估计方法，但本文通过举反例得到了不同的结论，对其可用性和实用性给出了负面的评价。

1 联邦滤波基本原理

1.1 集中Kalman滤波

随机线性系统的状态空间模型记为

(1)

式(1)中，是×1维的状态向量；是×1维的量测向量；-1、-1、是已知的系统结构参数，分别为×维的一步状态转移矩阵、×维的系统噪声分配矩阵及×维的量测矩阵；-1是×1维的系统噪声向量，是×1维的量测噪声向量，两者都是零均值的高斯白噪声向量序列，且它们之间互不相关，即满足

(2)

其中，是半正定的,是正定的，δ为克罗内克函数。

针对系统式(1)的Kalman滤波公式为

(3)

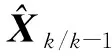
1.2 传统联邦滤波算法

假设式(1)可拆分成+1个子滤波器状态空间，分别记为

(4)

其中

(5)

(6)

(7)

传统的联邦滤波算法步骤如下。

(8)

(9)

3)Kalman滤波。各子滤波器(含主滤波器)进行Kalman滤波更新，如下

(10)

4)信息融合。综合所有子滤波器(含主滤波器)的结果，进行信息融合，如下

(11)

(12)

1.3 联邦滤波公式改进

(13)

2 一个简单系统举例

假设有一个含3个状态分量和2个量测分量的线性随机系统，记作CS，具体为

(14)

其中，1,、2,均为零均值的单位白噪声，且两者之间不相关；为时变元素。容易看出，系统式(14)不含系统噪声，3个状态分量为相互独立的随机常值，第一量测分量1,是状态1,、2,与噪声1,之和；而第二量测2,是状态1,、3,与噪声2,之和，1,为两量测共有的公共状态。因而，可将式(14)拆分成3个子系统，分别记为子系统S1、S2和主系统SM，具体如下

(15)

显然，如果为固定常值，系统S1和S2都是不完全可观的，即状态1,和2,之间、状态1,和3,之间相互耦合，无法单独分离；而若设置为时变的，则状态1,和3,之间可分离，从而也导致状态1,和2,之间可分离，最终使得3个状态分量都变为完全可观的。

(a)

(b)

(c)

(d)

(e)

(f)

从图1(a)、(c)、(e)可以看出，当<100时，由于系统不完全可观，两种滤波算法的3个状态分量均不能被正确估计；当>100时，因元素发生变化使系统变得完全可观测，集中滤波中的3个状态立即获得了正确估计，接近于真值曲线Xtrue。图1(a)联邦滤波的公共状态1,的估计结果虽然也有调整变化，但其估计值并不准确，结果明显是有偏估计；图1(c)子滤波器1(或图1(e)子滤波器2)的私有状态2,(或3,)的估计也都是有偏的。观察图1(b)，在=100后状态1,的均方差迅速减小，联邦滤波比集中滤波下降得更多，说明前者的估计精度虚高，致使在状态1,的估计出现偏差后就难以再往正确方向进行调整了。

3 传递对准举例

在组合导航的联邦滤波算法应用研究文献中，比较典型的例子是惯性/卫星/天文组合导航和速度+姿态匹配传递对准，两者都存在角运动和线运动两类量测量，可以拆分出两个子滤波器。这里以传递对准为例,验证联邦滤波的估计效果。

(16)

传递对准集中滤波器的状态空间模型为

(17)

其中

图2 失准角估计效果对比Fig.2 Misalignment angle comparison

两种滤波算法的传递对准仿真结果曲线较多，这里仅展示子惯导失准角估计结果，如图2所示。由图2可见，集中滤波算法的3个失准角估计效果均较好，水平失准角一开始就很快收敛，在10s开始摇翼机动后，方位失准角也快速收敛；然而，联邦滤波算法的3个失准角始终都存在较大偏差，不能正确收敛。对于其他状态的估计，联邦滤波算法的效果也不好，这里就不再一一展示了。

就前面所举的两个联邦滤波仿真例子式(14)和式(17)，读者可试着选择其他信息分配因子或除式(13)外的其他Kalman滤波均方差阵放大方式，只要进行了反馈重置，联邦滤波往往都很难取得理想的估计效果。从理论上不容易证明联邦滤波的不合理性，众多文献介绍联邦滤波是一种次优滤波方法，但并没有指出次优滤波会有多“次”；而文献[2]中“精度下降十分微小”的说法并不合适，本论文仅以举例仿真的方式验证了联邦滤波估计结果的不正确，相较于集中滤波，联邦滤波的次优估计精度往往是不可接受的。

4 结论

许多文献对联邦滤波及其应用进行了研究，甚至提出了信息分配因子优化、自适应联邦滤波、联邦滤波结构与容错性分析等一系列更复杂的改进措施，都声称获得了较好的应用效果，然而其程序代码实现不公开，他人无法复现效果，目前尚未见联邦滤波在实际组合导航产品中应用的实例报道。

本文通过两个例子:一个简单的3维系统和一个速度+姿态传递对准组合导航(详细程序代码可参见PSINSdemo est_federated_KF_simple_example3.m和test_align_transfer_fkf.m)，验证了联邦滤波是不可行的，难以获得正确的滤波估计结果。想要从理论上证明联邦滤波的不合理性，还是比较困难的。传统联邦滤波不是普遍成立的，在特定系统中或许可以使用，但是应当证明联邦次优滤波不至于太次，与集中滤波相比次优估计结果是可接受的，当然这种可用性条件的给出或证明也是比较困难的。因此，对于以精度为主要性能指标的组合导航系统，联邦滤波的实用性值得商榷。