圆筒式织物热湿舒适仪仿真模拟研究
2022-08-04熊巧玲董奕辰杜赵群
熊巧玲,董奕辰,刘 贵,杜赵群,林 旭
(1.东华大学 纺织面料技术教育部重点实验室,上海 201620;2.福建省纺织产品检测技术重点实验室(福建省纤维检验中心),福州 350026)
随着社会的日益发展和进步,人们对生活品质的要求越来越高。 而对于传统纺织服装行业,服装穿着的舒适性能在消费者心中是排在首位的。 根据数据显示,81%的纺织服装行业消费者认为纺织品的舒适性比服装的款式设计重要[1]。 而在我国服装舒适性已成为影响消费者购买服装的三大因素之一。 服装舒适性包括了热湿舒适性、接触舒适性以及视觉舒适性[2-4]。 热湿舒适性是指皮肤、织物以及空气之间通过织物的热湿传递作用,使人体在外界环境不断的变化下依然可以获得舒适满意的感觉,即达到人体体感平衡的一种状态。 在这种状态下既不感觉到寒冷、燥热、又不感觉闷湿,人体的各个器官和各项机能处于正常的状态[5],这就是人体—服装—环境系统的中和状态。
在研究织物及服装的热湿传递性能时,研究者大多在人体—服装(织物)—环境系统的基础上来探讨热量传递和水分传递的过程。 其研究内容主要可以概括为两类:一是热湿传递机理、影响热湿传递的因素、表征热湿性能指标等;二是热湿传递性能的测试方法及仪器[6]。 测试仪器的研究对于评价服装及织物的热湿传递性能有着至关重要的影响。 随着当今计算机技术的迅猛发展,计算机技术已经应用到了各个研究领域,其中计算机仿真模拟技术通过其大量复杂的计算,解决了原先无法完成的诸多事情。 仿真模拟通过构建相应的数学与物理模型,在赋予参数的条件下进行计算,具有快速、环保、成本低的优势。 可以利用其辅助测试仪器的研发以及对热湿传递过程进行预测。
织物及服装的热湿舒适客观评价法对其使用的测试仪器有极高的依赖性。 例如出汗热板装置虽然体积小,测试方便,但是其测试状态与人体着装时织物的状态的差异是最大的。 出汗暖体假人其测试系统复杂,价格昂贵,对于更多情况的模拟也较难实现。 因此可以综合两种仪器优点的出汗圆筒式测试仪器正在成为研究的重点,利用仿真技术对出汗圆筒进行设计优化可以为仪器的研制提供参考和指导。
1 出汗圆筒的仿真模拟
在圆筒式织物热湿阻仪中,实际是将人体各部分近似简化为圆柱状,同样的在数值模型值仍然采用这种方式。 与真实仪器不同的是,利用数值模型仿真可以避免大量重复的实验,并且可以使模型参数更接近人体。 人体的生物组织无法被一般的工程材料所代替,但是在数值模型中,能够随意设定其材料参数,使其性质与人体更加接近。 另外通过更改数值模型的参数或结构还可以比较圆筒式仪器的温湿度场。
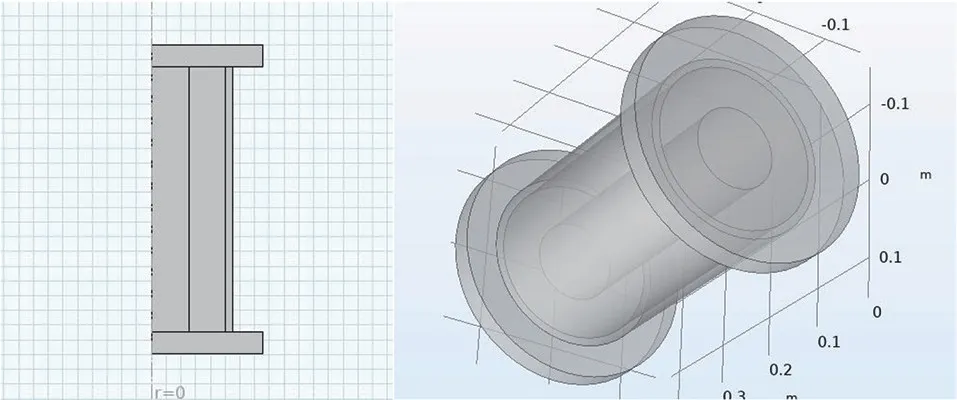
图1 出汗圆筒几何模型
要建立出汗圆筒的数值模型,需要对其进行以下假设:
(1)织物看作是均质的平板,整体具有相同的特性,且其热力学参数不随温度改变;
(2)导热主要在垂直表面的方向进行,不考虑层间的接触热阻;
(3)将各区域都视为各项同性的连续介质,空气与织物中固、液、气三相处于热力平衡状态,满足理想气体状态方程;
(4)只研究系统内的热湿传递过程,系统外的热湿传递过程按照传热传质理论中的对流边界来处理。
根据能量守恒和质量守恒,可以得到以下的热传递和湿传递的控制方程:
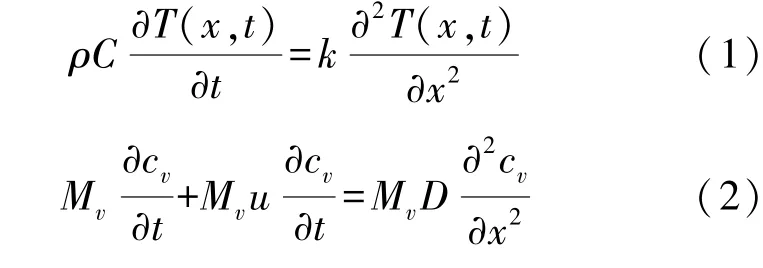
如果只考虑在圆筒内部的水浴温度达到设定的温度T0后的热湿传递过程,那么可以将圆筒内看作是等温域,初始值为T0,而微气候区热湿传递的初始值分布是环境的温度Ta和相对湿度RHa。
要对这个模型的热传递控制方程进行求解,只需要设置三个边界条件。 一个是织物与外界环境接触的边界,考虑外部自然对流的影响以及环境的辐射。 所以在边界条件类型中选择热通量边界,一个是隔热材料的边界,可以设置其热通量为0。 还有一个是圆筒仪的外筒壁,可以将其温度设置为固定值即筒内水浴温度。

mrsw是模拟皮肤的水汽蒸发速率,用防水透湿织物的透湿率来表示,通过实验测得,Rw是外层测试织物的湿阻,同样需要通过实验测得。 在进行数值模拟时这些参数都是已知的。
利用(3)~(7)的控制方程和边界条件公式,以及在模型中设置的初始值,就可以对模型的温度场和湿度场进行求解。 在求解时可以根据需要选用瞬态求解器或稳态求解器。
如果不将圆筒壁与模拟皮肤看成薄层结构,而是将其设置成具有一定厚度的域,并将该域内的参数设置为人体皮肤参数[7],见表1。
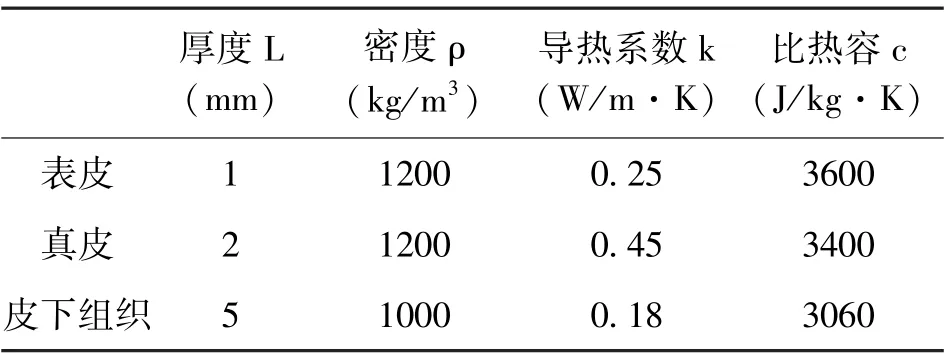
表1 皮肤组织的热物理参数
并将皮肤边界的边界条件即公式(6)中的mrsw采用Gagge 的出汗调节方程[8]代替。 其计算公式见(9),式中Tb为筒内水浴温度,T 则为新设置的皮肤域的温度。

1.1 出汗圆筒加热结构优化
在考虑对圆筒仪内部的水进行加热时,主要考虑了两种方案。 第一种是将加热丝缠绕在内筒上进行加热,另外一种是将加热丝盘旋固定在圆筒的底部和顶部进行加热。 为了了解那种方式更够更加均匀且快速地对圆筒仪内部的水进行加热,使水温能够达到PID 设定值。 将对两种方案进行仿真。
如图2 和图3 所示,当考虑将加热丝缠绕在内筒壁上进行加热时,圆筒仪内部水温在竖直方向上表现出良好的均匀性。 在圆筒附近的温度较高,圆筒中心和圆筒外侧的温度较低。 当加热丝附近温度为100℃时,外筒温度约为40℃。 而在考虑将加热丝盘旋固定在底部和顶部时,圆筒仪则是在水平方向上均匀性较好,而在竖直方向上的温差分布非常大。 当顶部的温度已经达到300℃时,圆筒中间的水位只有50℃左右。 虽然顶部和底座是绝热材料,但是仍然会产生较多的热量损耗,使加热时间延长。 圆筒式热湿阻仪要求外圆筒壁的温度能够均匀一致,所以从上面两张图的分析来看,采用加热丝缠绕在内筒的加热方式更好。

图2 内筒加热
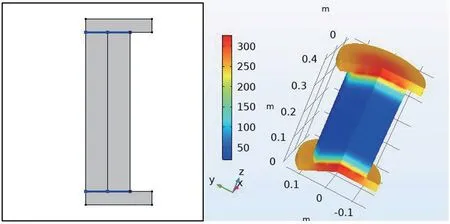
图3 顶部和底部加热
1.2 出汗圆筒外筒材料优化
在选择圆筒的材料时,内筒的材料对于测试过程的影响很小,所以使用耐用性好的金属材料即可。 而金属外筒与外界空气或者织物的距离很近,采用不同的材料有可能会对测试结果产生一定的影响。 金属外筒同样需要考虑其耐用性,铜和不锈钢在大气、淡水中都有良好的耐腐蚀性且强度高。所以初步确定采用铜(导热系数400W/m·K)和不锈钢材料(导热系数17W/m·K)作为金属外筒材料。
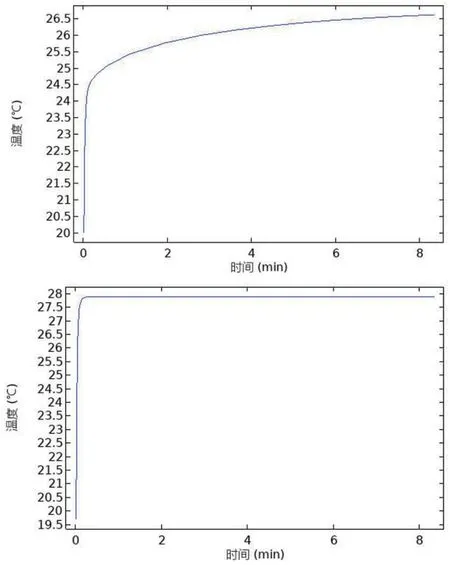
图4 织物内边界温度上升图
观察织物内边界的温度随时间的变化曲线,可以看到,使用铜作为外壁时,织物内边界的温度变化比使用不锈钢时温度的变化快。 在初始时刻织物与空气域的初始值都是20℃,使用铜作为外壁材料,在前2min 内织物处的温度就迅速增加到27.8℃。 而在使用不锈钢作为外壁材料时,在前1min 的温度升高比较快,随后升高速率逐渐降低。使用不锈钢材料,在热湿传递测试过程中,其热传递的状态更接近人体皮肤热传递状态,因此选用不锈钢材料更有利于在实验中观察温湿度的变化情况。
1.3 出汗圆筒外筒孔径优化
为了研究外圆筒壁孔径对于测试面温度分布的影响,将其转化为平板模型,在COMSOL 中进行建模分析。 如下页图5 中所示,建立了圆筒壁与防水透湿织物的双层平板模型,圆筒壁上有圆孔均匀分布,由于圆筒内部是水,所以圆孔内也是充满水的。 设置有孔边界面的温度为37℃恒温,织物外边界面为20℃的外部自然对流。 为在此分布用了2mm 和4mm 的孔径大小进行计算分析,其结果见图6。

图5 外圆筒壁及防水透湿织物平板模型
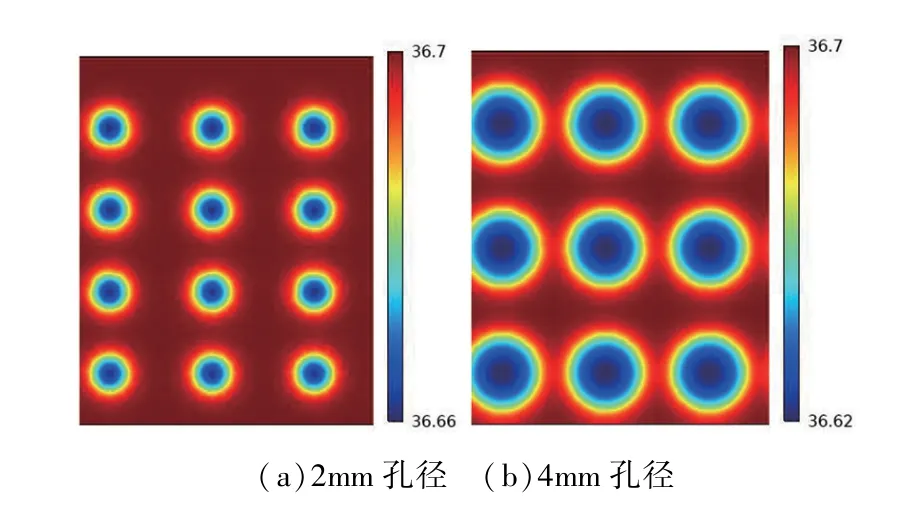
图6 表面温度分布
从图6 中可以看到,在模型的表面,温度是由圆孔中心向外递增的。 虽然采用2mm 的孔径与采用4mm 的孔径其最低温度与最高温度之间的差异并不大,但是仍然可以看出,孔径越大在达到稳态时织物表面的最低温度与最高温度之间的差越大。 由此可见,小孔径更利于使测试面温度的均匀分布,在加工时将采用可加工出的最小孔径来进行加工。
2 基于数值圆筒模型的预测分析
2.1 不同空气层厚度热湿传递预测及分析
若利用出汗圆筒式仪器进行测试,想要模拟人体穿着服装的状态,模拟皮肤与被测织物间应该留有一定厚度的空气层,形成微气候区。 但是其厚度一般较小,不便于在其间放置温湿度传感器。 无法观察在空气层中温度与湿度的变化情况。 一般微气候区的厚度小于12.7mm 时可以不考虑其内部自然对流的影响[9]。
仿真的环境工况条件为:温度为20℃,相对湿度65%,风速为<0.1m/s。 仿真对象棉织物参数为
热阻:0.0479W/(m·K)
湿阻:39.59m2·Pa/W
图7(a)是在空气层厚度分别为2mm、4mm、6mm 的参数条件下,同一节点处温度随时间的变化曲线。 从上图可以看出,随着空气层厚度的增加,达到平衡的时间越长,空气层内的温度也越高。图7(b)是在达到平衡后的空气层内温度分布,稳定后空气层内的温度接近线性分布,从左边界到右边界呈现下降趋势。 左边界的温度分别为35.5℃、35.8℃、36℃,说明在一定范围内增加空气层厚度可以提高保暖性。
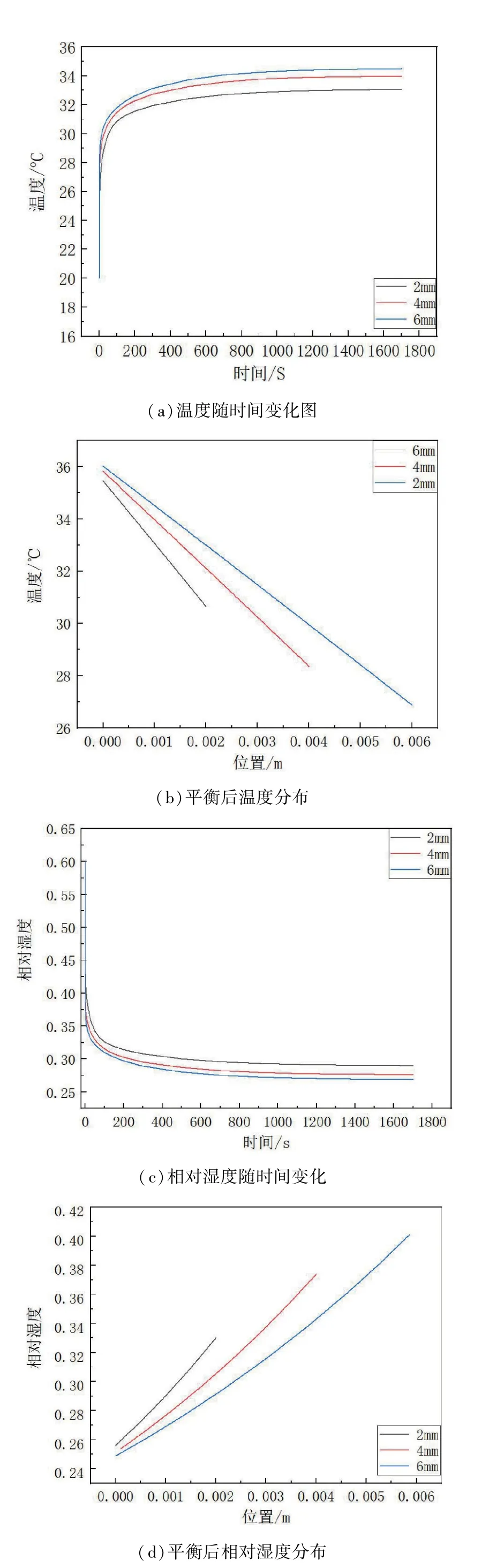
图7 不同空气层厚度下温湿度变化及分布
图7(c)表示的是衣下空气层厚度分别为2mm、4mm、6mm 时空气层内同一节点处相对湿度随时间的变化规律。 从图中可以看出在前2s 相对湿度迅速下降,之后下降速度变缓,并逐渐趋于平衡。 这是由于模拟皮肤在裸露状态下,附近水蒸气分压与环境中的水蒸气分压相平衡,而在加上织物与空气层后,空气层内的温度迅速升高,且从模拟皮肤边界到织物内边界呈逐渐下降趋势。 温度的升高会导致水蒸气分压增大,从而使相对湿度降低。 随着空气层厚度的增加,相对湿度达到平衡的时间越长,同一位置相对湿度越小。 从图7(d)平衡后空气层内相对湿度的分布可以看出,空气层中相对湿度从模型模拟皮肤边界到织物内表面边界是接近现线分布的,距离模拟皮肤越近,相对湿度越低,这也说明了在未出汗的情况下,穿着该织物制成的服装能够很好地保持皮肤干爽的感觉。
2.2 不同空气层厚度热湿传递预测及分析
一般情况下利用仪器进行测试时,较难把控环境的温度,必须要有非常专业的人工气候室才能实现在不同环境下的测试。 但是在实际情况中外界环境对于人体的穿着时的热湿舒适度也有很大的影响,要想描述一块织物的热湿舒适性,就要结合其实际环境。 例如对于一块热阻大的织物,如果是在较冷的环境中,我们会评价其热舒适性好。 但是在热环境中由于人体更需要一种凉爽的感觉,那么此时的热舒适性显然是不好的。 在本小节中将讨论在无风状态下温度和相对湿度对于空气层内热湿传递的影响。 仍以棉织物为例,衣下空气层的厚度设置为6mm,环境风速V<0.1m/s。
首先讨论在同样的相对湿度下,不同温度条件下空气层内同一节点的温度、以及相对湿度的变化规律。 环境条件分别设置为以下参数:
(1)环境温度T=10℃;环境湿度RH=60%
(2)环境温度T=20℃;环境湿度RH=60%
(3)环境温度T=30℃;环境湿度RH=60%
图8(a)是在相同湿度不同温度环境下同一织物和空气层的仿真结果。 在时间为0s 时空气层内左节点的初始值接近环境温度。 在不同的环境温度下,加上织物和空气层来模拟穿衣后,同一节点温度变化的趋势是一致的,都是先迅速升高后趋于平衡,但是可以看到随着环境温度的升高,开始时的温度曲线梯度越大,空气层内节点的温度升高越快。 当环境温度为30℃时,空气层中所选节点处的温度约2s 就达到平衡了,而当环境温度为10℃时,则需要大约12s。 图8(b)是达到平衡状态后空气层内的温度分布,在达到平衡状态后,模拟皮肤边界到织物内表面区间内的温度呈线性分布,环境温度越高斜率越小。 但是模拟皮肤表面的温度相差不大。 这也从侧面证实了织物及空气层的热调节功能。

图8 不同环境温度下空气层内温湿度变化及分布
图8(c)表示的是不同环境温度下空气层同一节点处的相对湿度随时间的变化趋势,可以看出,在不同的环境温度下,相对湿度的变化趋势大致相同,初始值都是环境相对湿度。 刚开始,由于热源的加热作用,温度的迅速升高,导致水蒸气分压迅速增大,相对湿度迅速下降。 而随着空气层内温度的升高,相对湿度的下降趋势也变缓。 图8(d)是达到平衡后空气层内相对湿度的分布,总体来看,相对湿度依旧是从左边界到右边界呈现递增的,但是环境温度越高,左边界与右边界相对湿度差异约小,且环境温度越高达到平衡后的相对湿度越高。
讨论完环境温度对于模拟结果的影响后,接着讨论在相同环境温度,不同相对湿度条件下空气层内同一节点的温度及相对湿度的变化规律。 环境条件分别设置为以下参数:
(1)环境温度T=30℃;环境湿度RH=20%
(2)环境温度T=30℃;环境湿度RH=60%
(3)环境温度T=30℃;环境湿度RH=90%
从图9(a)可以看出,当环境温度为30℃时,不同的环境湿度条件下空气层内同一节点的温度随时间的变化曲线基本重合,在达到稳态后空气层内的温度分布也一致。 因此环境相对湿度对于空气层内的温度变化基本没有影响。 从图9(b)空气层内相对湿度随时间的变化中,可以看出随着环境相对湿度的增加,空气层内相对湿度的变化趋势虽然一致,但是环境相对湿度约高,空气层内相对湿度达到平衡的时间越长,且与初始时刻的差异越大。同时,在达到平衡后,空气层的相对湿度分布也存在明显差异,环境相对湿度越大,空气层内相对湿度也越大,空气层左边界到右边界的分布梯度越大。

图9 不同环境相对湿度下空气层内温湿度变化
3 结论
利用仿真的方式对出汗圆筒内部加热方式以及外筒材质、孔径进行分析,用于出汗圆筒式仪器的优化。 内部的加热方式考虑内筒加热及筒底部加热,分析发现将加热丝缠绕在内筒上的加热方式能够更快达到设定温度,并且测试面的温度分布也会更加均匀。 外筒的材质考虑不锈钢和筒两种材料,分析发现使用两种材料的稳态圆筒温度分布差异不大。 但是使用铜作为外筒材质时,微气候区域温度升高较快,不利于对温度的监测,所以最终选择不锈钢作为外筒材料。 在分析外圆筒壁孔径对于测试面的影响时,测试面表面圆孔处的温度沿圆孔中心向外递减,所以选择更小的孔径有利于测试面温度的均匀分布。
在完成出汗圆筒的仿真设计后,利用构建的数值圆筒模型,对其在不同空气层厚度下以及不同环境工况下空气层内的热湿传递做了分析与预测。结果表明随着空气层厚度的增大,在数值模型的模拟皮肤边界的温度会越高,相对湿度会越低。 而在不同的环境温度下,随着环境温度的增加,模拟皮肤边界处的温度和相对湿度越大,空气层内温度和相对湿度分布梯度越小。 在不同的环境相对湿度下,环境相对湿度的增大,对于空气层内的温度变化影响很小,但是空气层内相对湿度的平衡时间延长,模拟皮肤边界的相对湿度增大,整个空气层相对湿度分布梯度也增大。
