BP神经网络预测架空覆冰导线气动系数
2022-08-04刘小会蔡萌琦闵光云
刘小会, 周 顺, 汪 顺, 蔡萌琦, 严 波, 闵光云,5
(1.重庆交通大学 土木工程学院,重庆 400074;2.重庆交通大学 省部共建山区桥梁及隧道工程国家重点实验室,重庆 400074;3.成都大学 建筑与土木工程学院,成都 610106;4.重庆大学 航空航天学院,重庆 400044;5.中山大学 中法核工程与技术学院,广东 珠海 519082)
0 引 言
在冬季,输电线在高空中由于温度过低会覆冰,进而导致输电线的截面由圆形截面转换为非圆形截面,当其受到来自水平方向的风荷载作用时,线路自身会产生气动荷载[1-3],由于气动荷载的存在,覆冰导线易发生舞动[4]。输电线舞动是一种低频、大振幅的自激振动,持续时间较长,易使得线路断裂、金具磨损、绝缘子串破裂,严重时会引起倒塔事故的发生[5-6]。
气动系数是研究覆冰导线舞动特征的一重要参数。文献[7]中利用前馈神经网络对风力发电的数据进行模拟训练,提高了风力的预测性能,验证了神经网络方法的可行性。文献[8]中利用K-means聚类和深度置信网络(DBN)进行短期风能的预测,与BP神经网络和Morlet小波神经网络预测结果相比,其预测精度明显提高;文献[9]中利用前馈神经网络,对飞行器纵向气动特性进行辨识,推导出辨识飞行器气动参数的导数法,并验证了两种参数辨识方法的有效性。文献[10]中提出了一种基于BP神经网络的舞动预警方法,采用舞动的相关数据分析比较,验证了该方法的有效性和实用性。文献[11]中采用卷积神经网络建立了圆柱压力和速度场间的关系模型,通过该模型只需测量钝体上的压力分布即可预测结构尾流速度场。文献[12]中利用支持向量机(SVM)识别了斜拉桥的颤振导数和颤振临界风速。文献[13]中通过人工神经网络技术,建立大跨度桥梁主梁气动参数的神经网络模型,结果表明神经网络输出与期望输出间的误差符合预期要求。文献[14]中根据有限的风洞试验测试结果采用神经网络方法预测未知点平均和脉动风压系数,以及脉动风压的自功率谱和互功率谱函数,其预测结果与实测值吻合得较好。文献[15]中改进BP神经网络算法,设计了初级概率预测器进行故障概率预测;最终表明该方法克服了特征参数少和样本数量不足造成预测结果不准确的问题。文献[16]中建立一种改进型BP神经网络的卫星钟差高精度预测方法,其中使用PSO算法对BP神经网络结构进行优化。最终发现改进后模型的预测精度明显优于常规的BP神经网络模型。
本文利用BP神经网络方法输电线在不同覆冰类型与不同风速的气动系数,并与风洞试验结果进行了对比,验证了BP神经网络方法的可行性,具有一定的工程应用价值。
1 覆冰导线风洞试验及气动系数测量
1.1 导线模型
由于地形、温度、风速以及导线结构参数等不同,单导线、四分裂导线的覆冰类型有多种。本文风洞试验导线的覆冰类型有新月形、扇形两种,以新月形覆冰四分裂导线为例,首先建立新月形覆冰四分裂导线在一定风速u的横截面模型,如图1所示。

图1 新月形覆冰四分裂导线横截面
1.2 风洞试验装置
风洞试验需要用到两种型号的天平,即TG0151A天平和TG0151B天平,用来测量分裂导线与单导线模型的阻力、升力。
风洞试验模拟的四分裂导线具体型号为4XLGJ-400/50,导线直径为27.6 mm。相邻导线间隔距离为450 mm,保证各导线在试验中不至于连至一起,且每根导线的参数和型号都一样。四分裂导线的试验模型布置在风洞中(1.4 m×1.4 m),风洞试验段长度为2.8 m。为了便于安装天平,导线模型与原型直径比例为1∶1.2,导线长度选择710 mm[17]。单导线参数与设备型号与四分裂导线一致,区别在于只使用1根导线且没有尾流效应的影响。
1.3 试验方法
试验主要测试单导线、四分裂导线在不同覆冰类型下,不同风速、风攻角(0~360°)的气动系数。使用图2静态导线测力试验装置,每隔5°测一次气动系数。
覆冰导线静态空气动力特性测得的气动系数包括升力系数CL、阻力系数CD、扭矩系数CM,无量纲的气动系数公式如下:
(1)
式中:FL、FD、FM分别代表导线试验模型中的升力、阻力、扭矩;uz为风速;ρair为试验时室温下的空气密度;L为导线模型的有效长度;d为导线模型的参考直径。

图2 静态测力试验装置
1.4 数据库建立
风洞试验测得的数据如下:
(1) 单导线。新月形覆冰在冰厚12、20、28 mm各自在10、12、14、18 m/s风速下的气动系数;扇形覆冰在冰厚18、25 mm各自在10、12、14、18 m/s风速下的气动系数。
(2) 四分裂导线。无覆冰下四分裂导线在10、12、14、18 m/s风速下的气动系数。
本文BP神经网络模型数据库选用风洞试验中的数据。首先,选取风洞试验数据的一部分作为训练数据,另一部分作为测试数据,将训练数据导入模型训练,生成预测数据,与测试数据相对比,观察BP神经网络预测的准确性。
2 神经网络模型的选择与参数设置
2.1 BP神经网络
多层感知器可以通过逐层的信息传递得到网络最后的输出a(L),整个网络可以看作一个复合函数Ø(x:W,b),将向量x作为第1层的输出a(0);将第L层的输出作为整个函数的输出[20]。
x=a(0)→z(1)→a(1)→z(2)→…
→a(L-1)→z(L)→a(L)=Ø(x;W,b)
(2)
式中,W、b表示网络中所有层的连接权重与偏置。
误差逆向传播算法是通过将误差分配给每个隐含层神经元,修正各个神经元之间的W和b,使误差信号趋于最小[21]。本文选取多层BP神经网络模型,其算法流程如图3所示。

图3 BP神经网络算法流程图
2.2 模型的构建
根据风洞试验结果,选择风速、风攻角、覆冰厚度作为模型的输入参数,与其对应的升力系数、阻力系数、扭矩系数作为输出参数,模型框架如图4所示。

图4 BP神经网络框架图
2.3 模型的参数设置
模型训练前先将输入数据预处理,即进行归一化处理。BP神经网络通常采用调解模型参数的方法来优化模型。本文通过选取模型网络层数与神经单元数、激活函数、学习率、随机数及切片数、训练次数作为调解参数。
(1) 切片数、训练次数。将训练数据使用Dataset类进行重构,划分为37、74或111大小的切片,每一个循环以切片大小数量打包为一组进行训练。模型进行切片划分数据,可以提高模型的计算速度。合适模型的训练次数可以提高模型的拟合能力,增强可预测性。本文采用试凑法,先采用较小的切片数和训练次数,通过观察Loss函数(见图5)下降情况,逐步增加切片大小与训练次数,直到Loss函数收敛到最小范围。
(2) 激活函数。激活函数采用Tanh激活函数,
(3)
Relu激活函数
Relu(x)=max(0,x)
(4)
Tanh函数是一般非线性问题常用的激活函数。本文通过多次调解激活函数的类型发现,Tanh函数在输入样本数据跨度较大时,得不到良好的训练模型,且对于层数较多、训练数据量较大的情况,Loss波动较大(见图6),但Relu函数很好地解决了这一问题。

图5 不同切片数下的Loss动态变化图

图6 不同激活函数下Loss动态变化图
(4) 学习率。对于学习率的调整可采用自适应方法。当学习率调节范围为(0,0.1)时,本文神经网络模型对数据的拟合能力较好。
(5) 损失函数。损失函数,又叫目标函数,是编译一个神经网络模型必须的要素之一。损失函数是指用于计算真实值和预测值之间差异的函数,在机器学习过程中,有多种损失函数。但对于回归类问题一般采用均方差损失函数(MSE),用来判断模型的预测值与真实值的差别,当误差较小时,经过平方后MSE所得到的反馈信号也越小,模型就会快速收敛到最小误差,
(5)
式中:N为样本数;yi为预测值;zi为真实值。
(6) 模型层数与单元数。通常情况下,所描述的神经网络模型为隐含层的层数及对应的每层神经单元个数,神经网络模型的选取没有明确的推导公式。本文在对比使用8×8、10×8、10×16模型后发现(见图7),隐含层神经单元过多,会增加计算的复杂性,很容易导致过拟合;隐含层神经单元过少,则会影响模型的训练能力,达不到训练结果要求。

图7 不同模型层数下Loss动态变化图
3 气动系数预测
3.1 单导线
3.1.1 新月形覆冰单导线
建立新月形覆冰单导线横截面模型如图8所示。

图8 新月形覆冰单导线横截面
以相同覆冰厚度的新月形单导线为研究对象,预测不同风速下单导线的气动系数。输入风速、风攻角,输出变量CL、CD、CM。详细工况如下:
IMM算法的输出是各个子模型输出结果以模型概率加权作为最终的滤波估计,各子模型依据马尔科夫链以一定的转移概率进行切换。因此,模型概率表征了子模型对目标运动的匹配度。本文采用了文献[2]的方法,实时修正模型概率。
如图9(a)、(b),试验值气动系数变化幅度较小、线性平缓,且无突变值,具有较好的预测结果;如图9(e),风攻角15°、20°处,由于数据突然变化,出现拐点,模型在完成训练后,对该点的预测值误差较大;如9(c),CL在(60~120)处;如图9(e),CM在(20~80)处,由于输入风速跨度较大,输出预测值后,尽管线性相似,但数据误差较大。但对于如图9(f),尽管出现一些拐点,但由于输入风速跨度相近,且在输入风速的区间内预测,在进行模型训练后,各组气动系数预测值与试验值误差均在范围之内,线性相似,满足预测结果期望。
如图10所示,新月形覆冰厚度12 mm、风速为14 m/s时的升力系数通过线性插值的方法与风洞试验、神经网络预测的结果进行对比。明显可以看出神经网络预测的拟合能力好,突出神经网络预测的优势。
(6)
式中:n为L、D、M;上标10、12、14代表不同的风速。
3.1.2 扇形覆冰单导线
建立扇形覆冰单导线横截面模型图,如图11所示。以相同覆冰厚度的扇形单导线为研究对象,预测不同风速下的气动系数。输入变量风速、风攻角,输出变量CL、CD、CM。
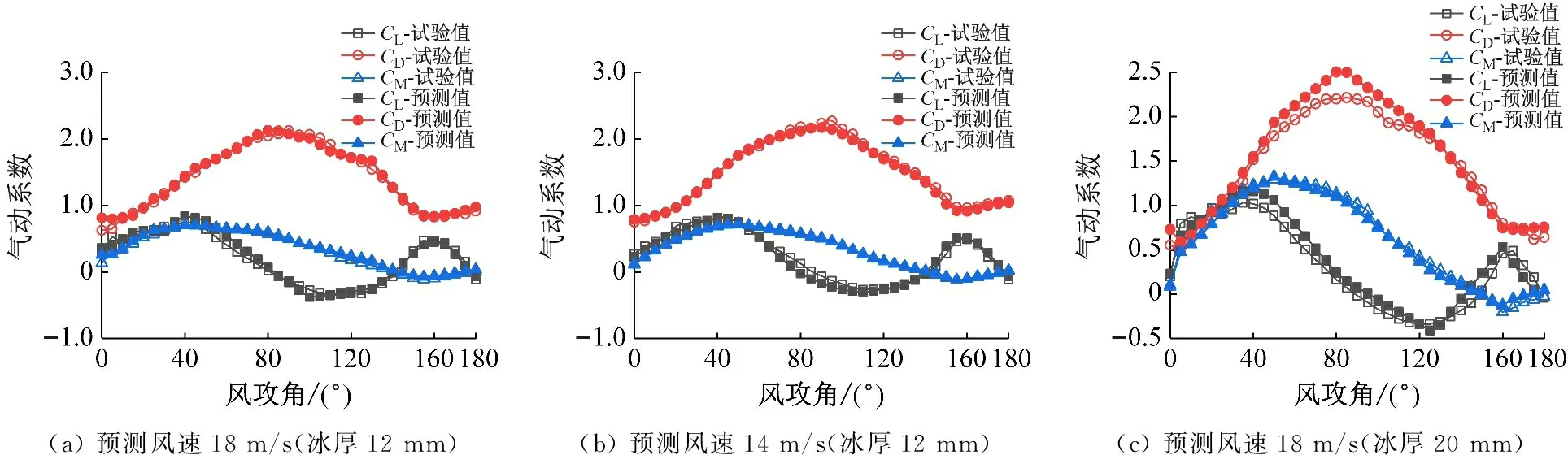

图10 线性插值与试验值、预测值气动系数

图11 扇形覆冰单导线横截面图
对于扇型覆冰单导线,将覆冰横截面简化成关于x轴对称、等厚度覆冰截面。在等厚覆冰、不同风速下,如图12(a)、(b)中,其气动系数变化情况大致相似,受风速影响较小;在不等厚覆冰、同种风速下,如图12(a)、(c)中,各组气动系数也只在个别点发生变化。但在进行神经网络训练时,模型会受到像新月形覆冰导线输入风速跨度大这种影响,在图12(a)、(c)中,CL表现极其明显,但预测的气动系数线性走向相似。在进行输入风速区间内预测,即图12(b)、(d),在进行神经网络预测训练后,其训练后的模型预测效果最好,可达到预测结果期望。

图12 不同风速下扇形覆冰单导线预测的气动系数
综合上述新月形、扇形覆冰单导线预测结果得出:神经网络预测时输入参数跨度越大其预测能力越差;在输入风速区间内预测,线性拟合能力强。
3.2 四分裂导线
本文的主要目的是检验BP神经网路对于输电线在风荷载作用下气动系数的预测能力,所以对于四分裂导线而言,只需要选取其中一根导线进行验证即可。本文选取四分裂导线子导线1来检验BP神经网络的预测能力。
3.2.1 无覆冰四分裂导线
建立无覆冰四分裂导线横截面模型图如图13所示。以无覆冰四分裂子导线1为研究对象,预测不同风速的气动系数。输入变量风速、风攻角,输出变量CL、CD、CM。

图13 无覆冰四分裂导线横截面模型
如图14(a)、(b)所示,14、18 m/s风速下CM数值很小,而且波动小;CL整体波动较小;CD值和波动情况比CL、CM大:0°~120°波动较小,120°~135°、170°~180°呈下降趋势;135°~150°呈上升趋势,150°~170°大致呈水平趋势。
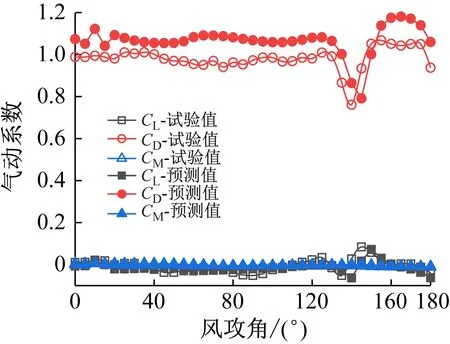
(a) 预测风速18 m/s子导线1气动系数
通过对比图14(a)与(b),在输入风速区间内预测的图14(b)效果更好;再单独对比图14(a)、(b)中的CL、CD、CM,可以看出波动小的CL、CM比波动大的CD效果好。
3.2.2 新月形覆冰四分裂导线
建立新月形覆冰四分裂导线横截面模型,如图15所示。以相同覆冰厚度的新月形四分裂子导线1为研究对象,预测不同风速的气动系数。输入变量风速、风攻角,输出变量CL、CD、CM。
如图15(a)、(b)所示,CL在0°~30°、115°~150°呈上升趋势,30°~115°、150°~180°呈下降趋势;CD波动较大,0°~90°呈上升趋势,90°~130°呈下降趋势、130°~180°呈波形下降趋势;CM总体波动较小。如图15(c)、(d)与图15(a)、(b)相比,其气动系数线性趋势几乎一致,只是前者在10°处气动系数出现拐点:图15(c)拐点较大,图15(d)拐点较小;在130°~180°之间前者比后者波动性小。如图15(e)、(f)所示,其气动系数趋势与图15(c)、(d)相似,只是前者气动系数在10°处拐点更大,在130°~180°之间波动性小。
如图15(a)~(f)所示,波动大的CD的预测效果比波动较小的CL、CM预测效果差。再如图15(a)、(c)、(e)和图15(b)、(d)、(f)这两组对比,很好地检验了输入风速跨度相近,且在输入风速区间内预测其效果越好;输入风速跨度大、数据波动性大,则预测效果不佳。
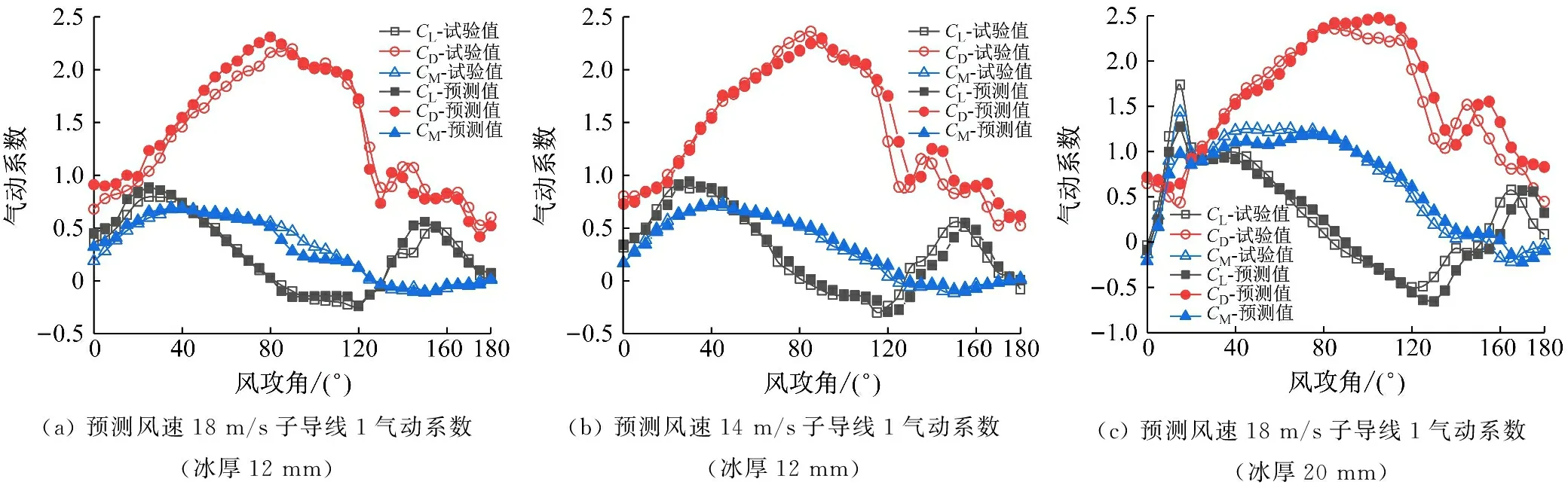
图15 预测不同风速下新月形覆冰四分裂导线1气动系数
3.2.3 扇形覆冰四分裂导线
建立扇形覆冰四分裂导线横截面模型,如图16所示。以相同覆冰厚度的扇形四分裂子导线1为研究对象,预测不同风速的气动系数。输入变量风速、风攻角,输出变量CL、CD、CM。

图16 扇形覆冰四分裂导线横截面
如图17(a)、(b)所示,CL在0~40、90~145°呈现下降趋势,40°~90°、145°~180°呈现波动式上升趋势;CD在0°~40°呈下降趋势,40°~100°时有较小波动,100°~180°呈现正弦式波动;CM在0°~40°、80°~100°呈现缓慢下降趋势,40°~80°呈现上升趋势,100°~180°呈现正弦式波动下降趋势。如图17(c)、(d)所示,其气动系数变化趋势与图17(a)、(b)大致相同,但是CD比后者的CD波动小很多。
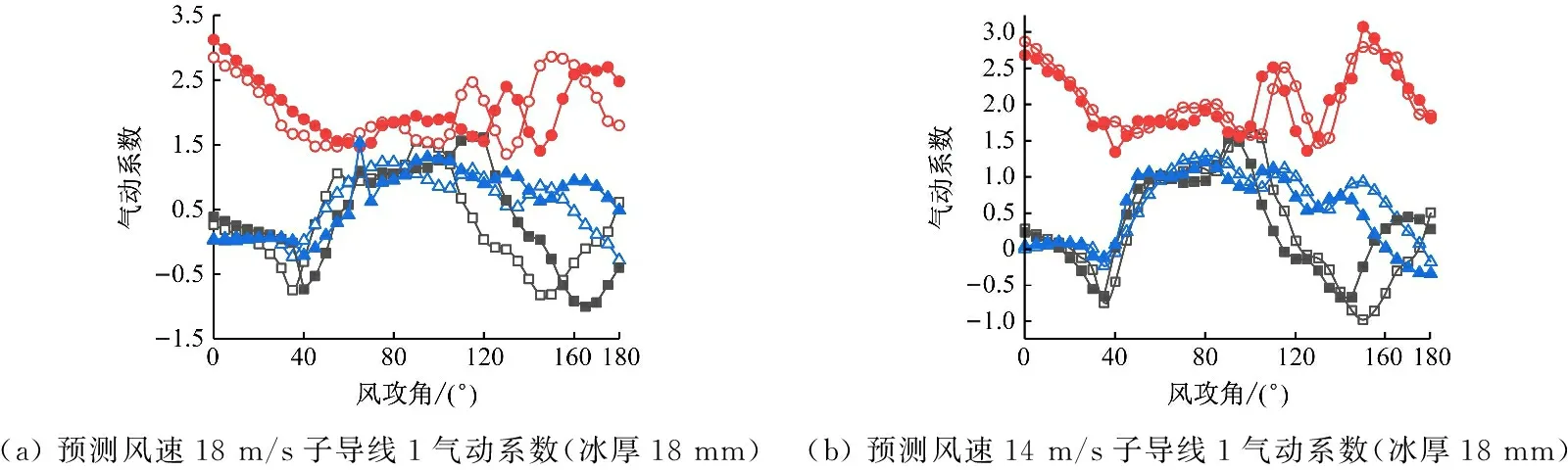
图17 预测不同风速下扇形覆冰四分裂导线1的气动系数
如图17(a)、(d)所示,波动大的CD预测效果比波动较小的CL、CM预测效果差。如图17(a)、(c)与图17(b)、(d),这两组对比明显后组效果好,再次验证了输入风速跨度大,则预测效果越差。
3.2.4 不同厚度下新月形覆冰四分裂导线预测
新月形覆冰四分裂子导线1在不同覆冰厚度下、预测不同风速的气动系数。输入变量覆冰厚度、风速、风攻角,输出变量CL、CD、CM。以下取新月形覆冰10 m/s风速进行检测预测效果。
如图18(a)所示,CL在风攻角为10°、15°、40°、125°、165°及175°时出现拐点;CD在120°、135°、150°出现拐点;CM在10°、15°出现拐点。通过对比上述拐点处的预测值与试验值可以看出,在拐点处预测效果较差。通过对比图18(a)与图20(b),在0°~20°之间,图18(b)不仅没有拐点且气动系数波动较小;再对比预测结果:图18(b)的预测效果比图(a)效果好。
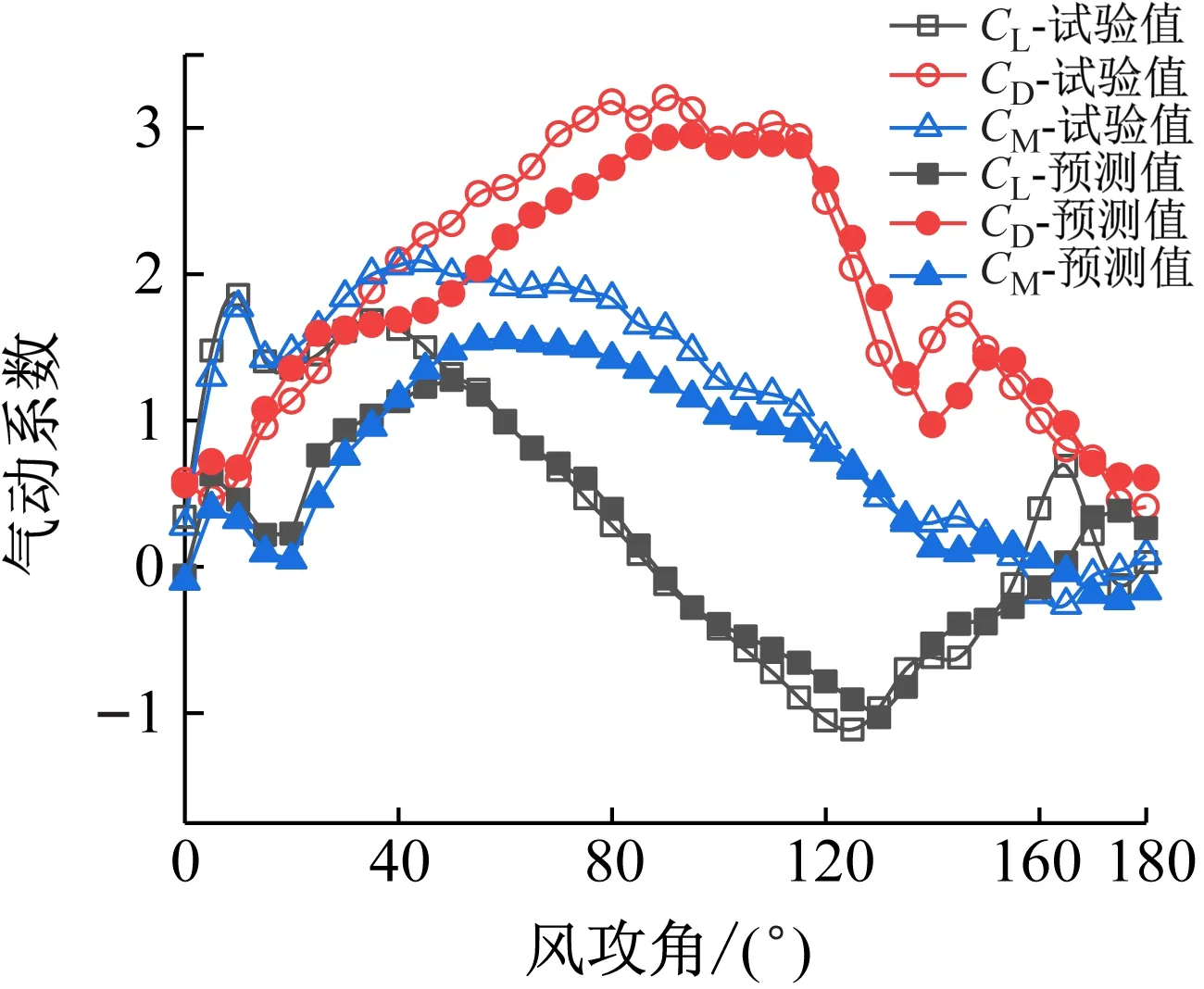
(a) 预测28 mm覆冰子导线1气动系数
综合上面无覆冰,覆冰(新月形、扇形不同厚度下)四分裂子导线1的预测效果图可以得出:神经网络预测时输入参数跨度大,其预测能力越差;神经网络预测模型中原始数据波动性越大、拐点越多、规律性越差,其模型的预测能力越差;神经网络模型输入数据库数量越大其模型拟合能力一般情况下就越强。
4 结 论
(1) 本文构建了BP神经网络的输电线覆冰风荷载下的气动系数的预测模型,通过对模型的训练测试与优化调参,得到了学习效率与泛化能力较强的预测模型。
(2) 神经网络模型的搭建对训练本身至关重要,对于数据较多、且线性规律不明显训练集,选择较大的隐含层层数和神经单元个数,可以提高计算精度,降低网络误差,减少模型的训练次数与训练时间。
(3) 由于覆冰四分裂导线存在尾流效应的影响,其气动系数数据与覆冰单导线数据相比,波动较大,规律性较差,在模型训练过程中的拟合能力不如单导线。因此,BP神经网络预测时输入参数波动越大其预测能力越差。
(4) 新月形覆冰导线有3组输入风速,对比扇形覆冰导线的两组输入风速,前者拟合能力明显较好,即输入样本数越多,神经网络拟合能力越强。
(5) 从仿真实例中的单导线、四分裂导线的预测图示,可以看出,BP神经网络的预测值与风洞试验的试验值拟合效果较好,再次验证了BP神经网络对架空覆冰导线气动系数预测的可行性。
