多时间尺度下含混合储能的生物质能CHP微网滚动优化
2022-08-04杨晓辉李昭辉周斯易
杨晓辉, 张 亮, 李昭辉, 周斯易
(1.南昌大学 信息工程学院,南昌 330031;2.国网江西省电力有限公司湖口县供电分公司,江西 九江 332500)
0 引 言
随着能源需求的增加,热电联供系统(CHP)集供热和供电于一体,比传统供热电分供系统更具吸引力[1]。CHP型微网有着较好的能源利用率与调度灵活性,是较有发展前景的一种运营模式[2]。含生物质能的CHP通常将木质颗粒化或 气化为燃料,燃料的来源十分广泛[3]。文献[4-5]中提出基于Minimax准则设计含生物质能的CHP系统,为本文后续的工作奠定基础。
为了将电力系统能源选择多样性提高,越来越多研究关注于风、光和生物质能的混合等可再生能源系统[6]。然而可再生能源的间歇性和波动性对电网的稳定性和安全性将会产生负面影响[7]。能量存储系统是处理可再生能源不确定性的有效技术之一[8],会对电力系统产生巨大影响。目前有许多研究聚焦在扩展规划、经济调度、机组组合问题和系统控制策略上[9]。文献[7]中提出了不同配置的混合储能系统,如蓄电池-超级电容器,蓄电池-超磁电机,压缩空气-飞轮,压缩空气-蓄电池和燃料电池-超级电容器等。然而较多文献在处理储能系统时只选择了简单的控制策略:发电量多余负荷量时,多余电量存储在储能系统中,当电量不足时,储能系统放电。大多数文献没有考虑储能系统的退化成本,文献[10]中对储能系统退化成本的处理比较粗略甚至直接忽略。文献[11]中构建了住宅混合储能的多种可再生能源系统,提出考虑需求响应的综合能源管理方法。
目前的优化调度方法主要都是对单个时间断面上的优化,在不考虑时间断面的耦合性的情况下,仅达到当前调度周期的最优,受风光等不确定性因素的影响较大[12]。因此,需要一种能够在不同时间尺度下实现不同目标的能量管理方法。文献[13]中提出利用模型预测解决多目标问题,上层解决微电网的最优规划,下层解决微电网的能源管理优化。文献[14-15]中利用模型预测控制解决微电网的机组组合问题。这表明模型预测控制的方法运用到微电网是常用的,并且能够考虑时间断面的耦合性。
本文设计了在多时间尺度下含混合储能的生物质CHP微网滚动优化模型。考虑混合储能系统的退化成本模型,包括蓄电池的退化成本模型和超级电容器的退化成本模型。利用蓄电池-超级电容器储能系统处理可再生能源不确定性。设计了多时间尺度下含混合储能的生物质CHP微网滚动优化模型,日前滚动(24 h/1 h)考虑微网的经济性,日内实时滚动(60 min/5 min)考虑预测误差导致的功率波动,并且分析了日内不同预测时域的影响。
1 含混合储能生物质能的CHP型微电网模型
1.1 生物质能CHP型微电网结构
生物质能是利用生产活动中产生的有机废弃物进行能量转换,常用气化方式进行发电。由于来源丰富以及价格便宜,因此应用前景较好。
相比于常规型微电网,CHP型微电网集供热和供电等功能联合运行效率较高,是最有发展前景的能源系统形式。电负荷可由发电装置和配电网供电,热负荷由余热锅炉提供。如图1所示,其发电装置包含了风电机组、光伏机组、蓄电池、超级电容器和配电网。
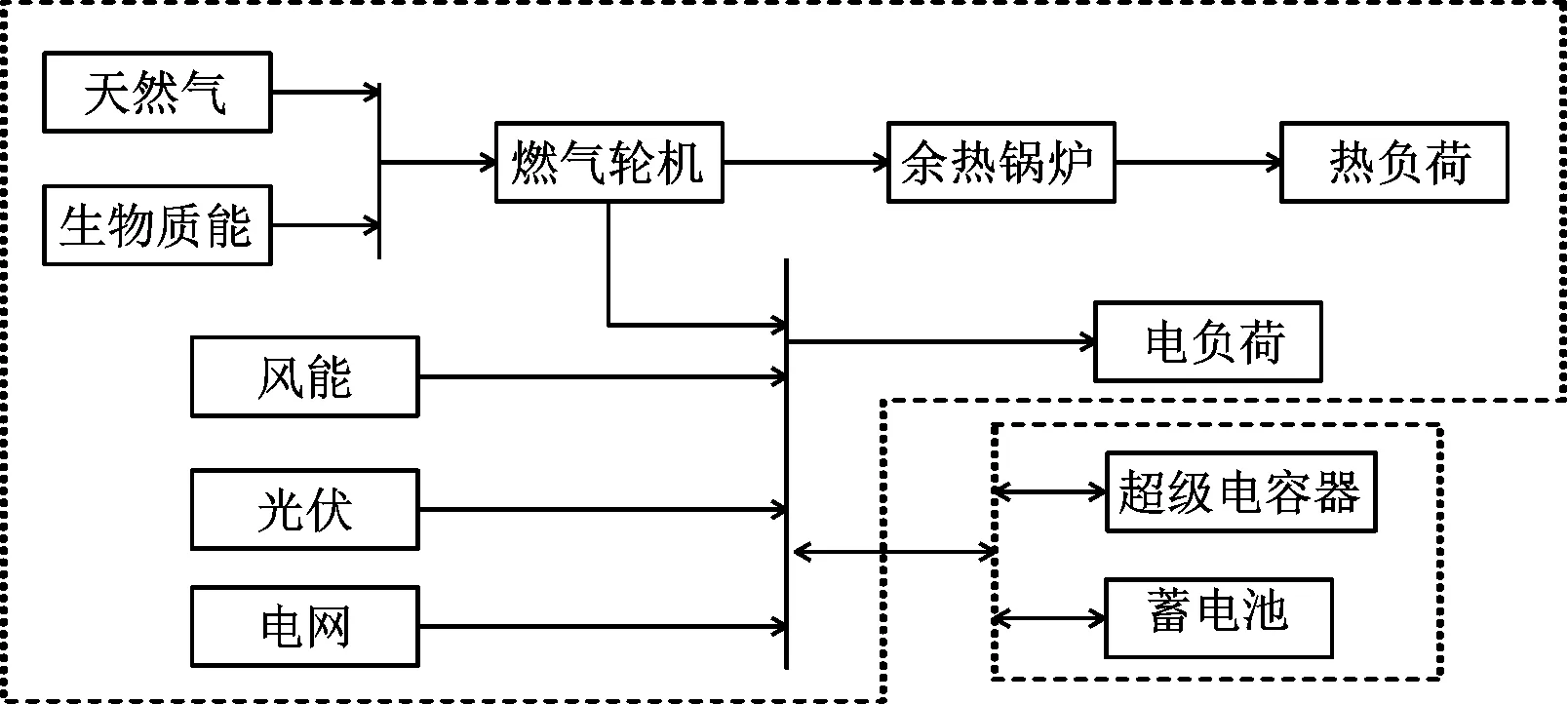
图1 生物质能CHP型微电网结构
1.2 生物质能CHP型微电网设备模型
(1) 燃气轮机。燃气轮机的排出废气余热功率数学模型:
(1)
燃气轮机的运行约束模型:
Pgt,min≤Pgt(t)≤Pgt,max
(2)
式中:ηgt是燃气轮机的发电效率;ηgt,l是燃气轮机的热损失系数;Pgt(t)是燃气轮机的输出功率;Pgt,min和Pgt,max是燃气轮机的最小和最大发电功率。
(2) 余热锅炉。余热锅炉输出热功率模型:
Qwh(t)=Qwhin(t)ηwh
(3)
余热锅炉的运行约束模型:
Qwh,min≤Qwh(t)≤Qwh,max
(4)
式中:Qwhin(t)是余热锅炉的输入热功率;ηwh是余热锅炉的效率;Qwh,min和Qwh,max是余热锅炉的最小和最大输出热功率。
热电比V是CHP机组输出热功率和电功率的比值:
V=Qwh(t)/Pgt(t)
(5)
(3) 可再生能源。由于风力发电与风速密切相关,风速随季节甚至天数而变化;光伏与光照密切相关,因此风光发电具有很强的不确定性。由于预测精度会随预测时域缩短而减小,通过研究日前滚动优化、日内实时滚动优化的多时间尺度协调优化,有利于提高风光利用率,减轻电网运行压力。设风光发电预测误差由均值为零且相互独立的正态分布刻画[16],即
(6)
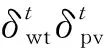
1.3 考虑退化成本的混合储能系统
新能源存在的波动性、间歇性和随机性特点,会给系统的功率平衡以及电能质量带来较大影响,蓄电池-超级电容器混合储能系统可以较好的平抑功率波动。蓄电池以其能量密度高的特点而广泛应用于储能领域,但其功率密度较小,动态响应速度慢,难以提供较大的瞬时输出电流,寿命较短。超级电容器能量密度较小,功率密度大,可承受短时高倍率充放电电流。
(1) 蓄电池。放电深度(DOD)是指一次充电或放电的能量与蓄电池容量的比值。蓄电池的使用寿命与其工作方式密切相关,往往放电深度越大,使用寿命越短。蓄电池的循环寿命与蓄电池的放电深度关系可以由拟合曲线表示[17]:
N(Dod(t))=a·Dod(t)-b·e-cDod(t)
(7)
式中:a、b和c是拟合曲线的系数;Eb是蓄电池总能量。由于之前的工作并没有具体的关系,因此合理地通过经验数据对蓄电池退化效应进行拟合。
由于蓄电池的退化成本与放电深度有关,便需要知道在相邻的时间间隔蓄电池的充放电状态。设U(t)是一个二进制数,值为1时表示蓄电池相邻时间间隔充放电状态不一致;值为0时表示蓄电池相邻时间间隔充放电状态一致。则从状态转换开始至t时刻所积蓄的能量:
(8)
则t时刻的放电深度可表示为
Dod(t)=Ea(t)/Eb(t)
(9)
同时,蓄电池实际容量会随着放电深度的变化而按比例退化:
(10)
式中,Erat是蓄电池的额定容量。
因此蓄电池的退化成本可表示为
(11)
式中:Cexb是蓄电池的更换成本;ηbc、ηbd分别是蓄电池的充放电效率。
(2) 超级电容器。通常情况下,超级电容器的退化成本可以认为是时间的线性函数[18],
(12)
式中:Cexsc是超级电容器的更换成本;Nsc是超级电容器的循环寿命。
2 多时间尺度滚动优化模型
2.1 多时间尺度滚动优化框架
滚动优化是有限时域内的优化,在当前时刻开始时输入此时的预测信息,进行本时段内的优化,而当下一个时刻到来时,将预测信息进行更新,来降低预测误差对调度结果的影响,如图2所示。
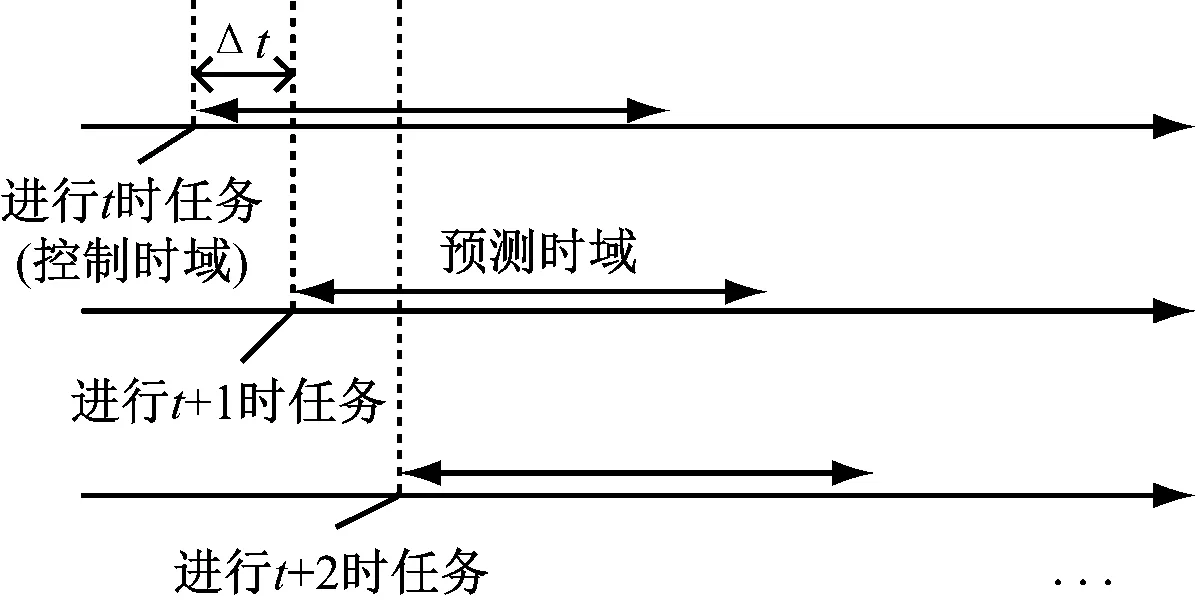
图2 滚动优化的时间窗口
日前滚动优化是以预测时域24 h、控制时域1 h,进行24轮优化控制,给出生物质能CHP型微电网的调度策略,主要是对微电网的经济性进行优化,通过不同设备的出力来协调热电功率平衡,给日内优化提供参考数据;日内实时滚动优化是以预测时域60 min、控制时域5 min,进行12轮优化控制,通过更新可再生能源的出力数据,对平抑风光误差,减小功率波动进行优化,多时间尺度滚动优化框架如图3所示。
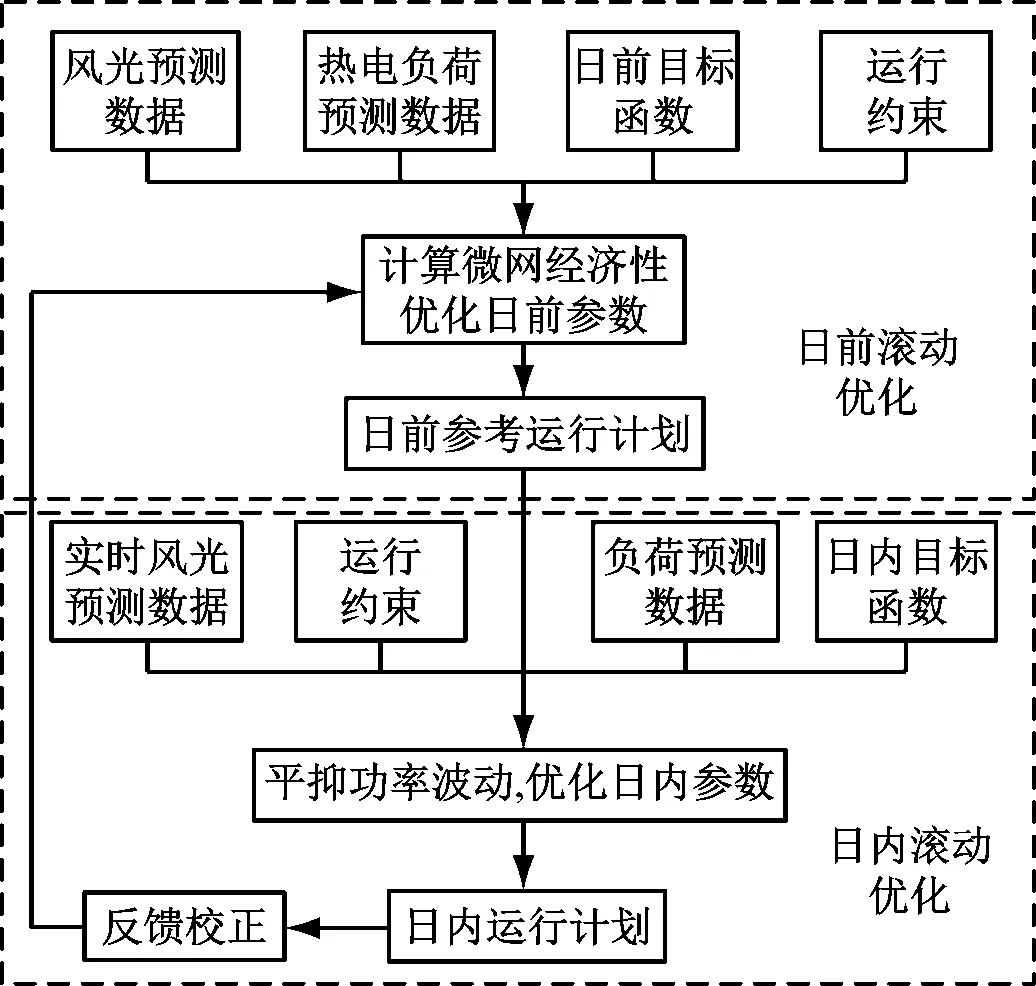
图3 多时间尺度双层优化框架
2.2 日前优化模型
(1) 目标函数。日前优化以系统总运营成本最小,包括与电网交互成本、电池退化成本及燃料购买成本。值得注意的是在日前优化中不考虑超级电容器,超级电容器仅在日内实时滚动优化时考虑用来平抑风光误差。
(13)
式中:
x∈[Pex(tDA),Pb(tDA),Pgas(tDA),Pbio(tDA)]
Pex(tDA)为与电网交互功率;Pgas(tDA)、Pbio(tDA)分别为利用天然气和利用生物质能产生的电功率;tDA是日前的控制时域。
Cex(tDA)=λex(tDA)Pex(tDA)Δt
(14)
式中:λex(tDA)是实时电价,为了保护电网利益,当微网电量有余时向电网售电的电价为0.8倍的实时电价。
(15)
式中:Qgas和Qbio分别为天然气和生物质能的低热值;λgas、λbio分别是天然气和生物质能的能源价格。
(2) 约束条件。日前优化约束包括等式约束和不等式约束,等式约束包括热负荷平衡和电负荷平衡,不等式约束包括一系列的设备运行约束。
电负荷平衡:
(16)
热负荷平衡:
VPbio(tDA)+VPgas(tDA)=Qheating(tDA)
(17)
式中,Qheating(tDA)是系统热负荷。
设备运行约束:
Eba(t)=
(18)
(19)
(20)
(21)
(22)
2.3 日内优化模型
(1) 目标函数。日内优化在进行优化前导入日前优化的数据[Pex(tDA),Pb(tDA),Pgas(tDA),Pbio(tDA)]ref,并且更新风光出力数据,优化因超电容器平抑功率而导致的变化。即
(23)
式中:
xDI∈[Pex(tDI),Pb(tDI),Pgas(tDI),Pbio(tDI),PSC(tDI)]
Cpu(tDI)是日内优化结果与日前结果波动的惩罚项;
δ2(Pex(tDA)-Pex(tDi))2+δ3(Pgas(tDA)-
Pgas(tDi))2+δ4(Pbio(tDA)-Pbio(tDI))2)
(24)
式中,δ1~δ4是惩罚成本系数。
(2) 约束条件。日内优化包含日前优化的所有约束条件,此外还应对电负荷平衡进行修正:
(25)
超级电容器运行约束:
Esca(t)=
(26)
(27)
(28)
2.4 模型求解伪代码
本文的计算平台采用CPUi3-4130、3.40GHz的Windows10电脑,日前及日内问题的求解均采用Matlab优化工具箱中求解非线性多元函数最小值的fmincon函数。模型求解伪代码如图4所示。

1. 导入系统相关参数,设置储能系统初值[Sstartb,Sstartsc],初始化xDA∈[Pex(tDA),Pb(tDA),Pgas(tDA),Pbio(tDA)]tDA+24tDA2. While tDA>24 h3. 更新tDA至tDA+24 h的风光预测数据,读取Sb(tDA),求解min fDA(xDA)4. 设置日内实时滚动优化初值:xstartDt=xDA(1,:)5. While tDI>60 min6. 更新tDI至tDI+60 min的风光预测数据,读取[Sb(tDI),Ssc(tDI)],求解min fDI(xDI),得到xDI∈[Pex(tDI),Pb(tDI),Pgas(tDI),Pbio(tDI),PSC(tDI)]tDI+60tDI7. 实时调度指令:x=[x,xDI(1,:)]8. 设置下一轮日内实时滚动优化初值:xstartDt=xDI(2,:)9. tDI=tDI+510. end11. tDA=tDA+112. 设置下一轮日前滚动优化初值:xstartDt=xDI(2,:) 反馈储能系统信息[Sb(tDI),Ssc(tDI)]13. end
3 算例分析
3.1 参数设置
算例模拟典型热电联供系统的能源配置形式,本文不考虑因天然气和生物质能比例对燃气轮机燃烧机制的影响。微网系统参数见附表A1。
日前滚动优化的控制时域为1 h,日内实时滚动优化的控制时域为5 min。日前预测数据见附图A1,日内预测数据在日前预测数据的基础上设置10%~50%的预测误差得到。电价采用分时电价,电价见附表A2。
3.2 结果分析
日内预测时域的长短影响系统的稳定性和快速性。表1展示了在不同预测时域下的系统日成本、蓄电池日退化成本和计算时间。随着预测时域的增加,系统日成本变化较小,蓄电池日退化成本逐渐减小,而计算时间却逐渐增加。为兼顾综合性能,本文设置日内预测时域为60 min。

表1 日内不同预测时域下的成本和计算时间
当系统热负荷完全由生物质能提供且日内预测数据设置为10%的预测误差时,其调度结果如图5、6所示,图5是日前滚动调度结果,在日前滚动优化中没有考虑预测误差的影响,也就不需要考虑超级电容器的协同,图6是日内实时滚动优化的调度结果,引入超级电容器来弥补误差,在不违背日前优化调度结果的同时,又能减少风光不确定性对系统造成的影响。对比两层的调度结果,可以观察到日前计划以小时为时间尺度,调度粗放,系统不能及时响应可再生能源波动,日内实时滚动优化中与电网交互功率、蓄电池功率和生物质能输出功率较上层波动较小,而超级电容器则随时间变化快速充放电以实现由预测误差导致的功率不平衡问题。此外对比附录B中20%~50%预测误差的日内实时滚动调度结果可知,在风光数据波动时,该系统能较好的保持日前的调度策略,同时也能较好地追踪风光的波动。

图5 日前实时滚动调度结果

图6 日内实时滚动调度结果
同时,蓄电池的运行主要由实时电价决定,在电价非峰期进行充电,在电价峰期进行放电。此外,在12:00~18:00这个阶段电价处于平价期,蓄电池一直处于充电状态,因为风光发电机组在这一阶段的发电量增多,使系统的发电量多于负荷。这说明蓄电池能紧随电价变化从而减少系统运行成本。
图7显示了蓄电池和超级电容器SOC的变化,蓄电池SOC的变化频率与超级电容器相比大大降低,这使超级电容器的瞬时消纳功能得到充分利用,并降低对蓄电池的冲击。随着预测误差的增加,蓄电池表现地较为稳定,波动并不明显,而超级电容器波动较大,这也体现了超级电容器的瞬时消纳功能能够响应不同的预测误差。与此同时,在8:00~16:00这个时间段内蓄电池和超级电容器的波动较大,这是由于光伏发电机组和风力发电机组在此时间段的不确定性更高,主要是光照风速原因使得可再生能源的输出存在较大波动。
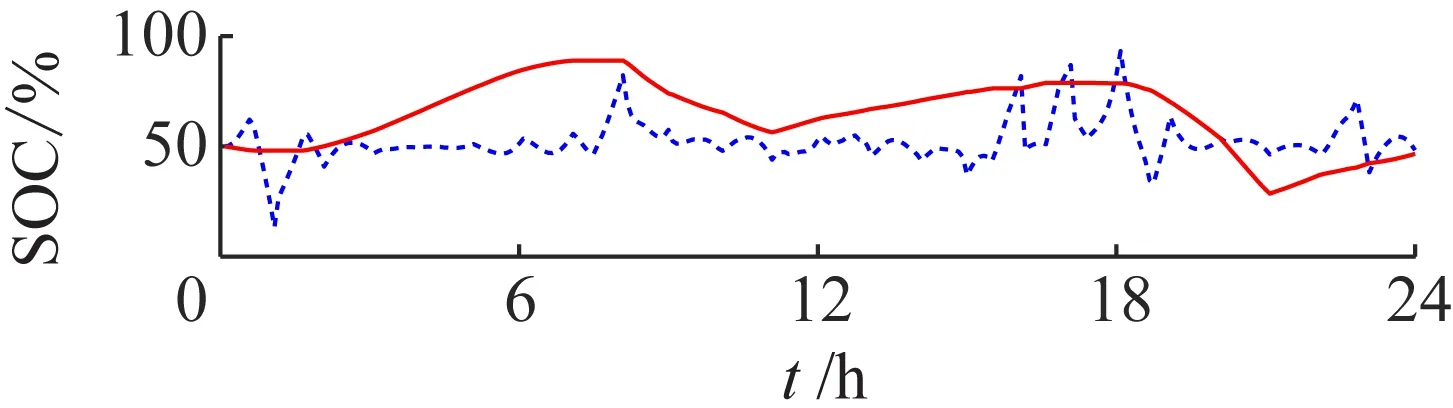
(a) 10%误差
表2列出了在不同预测误差情况下,系统用混合储能和单储能的蓄电池日退化成本。混合储能在应对不同的预测误差时蓄电池的日退化成本表现地较为稳定,而单储能时蓄电池的日退化成本随着预测误差增大而上升,而且混合储能对比单储能的蓄电池日退化成本节省百分比均在6%以上。

表2 混合储能与单储能蓄电池日退化成本对比
图8、9显示了在不同预测误差下系统运行成本和蓄电池退化成本的变化。可以看出,在日前日内实时滚动优化机制下,预测误差对系统运行成本影响较小,蓄电池退化成本稍微有些波动,但从日退化成本上看,预测误差影响较小,有利于系统控制成本。值得注意的是,蓄电池的退化成本在6、15和21 h几个时间段上偏高。从调度结果上可知,在这几个时间段蓄电池处于充放电状态过渡阶段或是放电深度较大,这也表明了蓄电池频繁充放电及较大的放电深度会增加蓄电池的退化成本,减少电池寿命。

图8 不同预测误差下系统运行成本
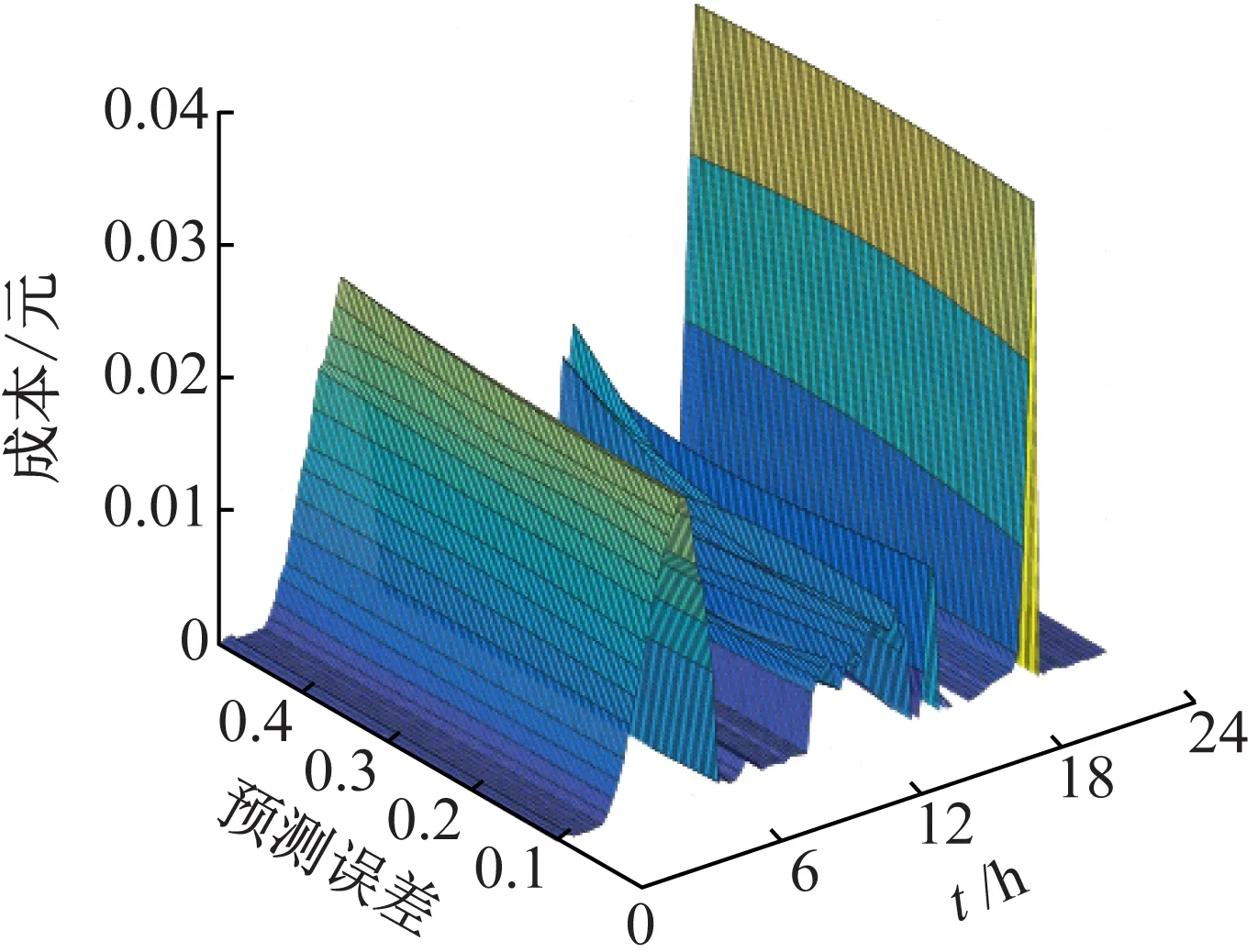
图9 不同预测误差下蓄电池退化成本
图10所示为天然气和生物质能不同比例时系统的运行成本。由图可知,当天然气所占能源比例逐渐升高时,系统的运行成本也逐渐升高。当系统热负荷完全由生物质能提供时系统运行成本取得最低值。这表明生物质能在滚动优化竞争中优于天然气,能够降低系统用能费用。然而由于生物质能的低热值远低于天然气,在不考虑价格的情况下,需要更多的生物质来源,这也将限制生物质能的应用局限于生物质能丰富的城镇乡村微电网系统。
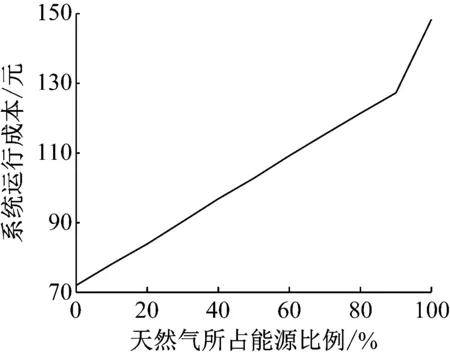
图10 不同能源比例时的系统运行成本
4 结 语
本文针对生物质能CHP微电网系统,引入考虑退化成本的混合储能模型,考虑光伏、风力及生物质能多种能源输入的微网联合运行优化模型,提出基于多时间尺度下的综合能源运行滚动优化方法,日前滚动优化微网经济性,日内实时滚动优化因预测误差引起的功率波动。在算例中,针对不同的预测误差,分析系统的调度结果及储能状态,验证了所提模型的有效性和经济性。
附录A
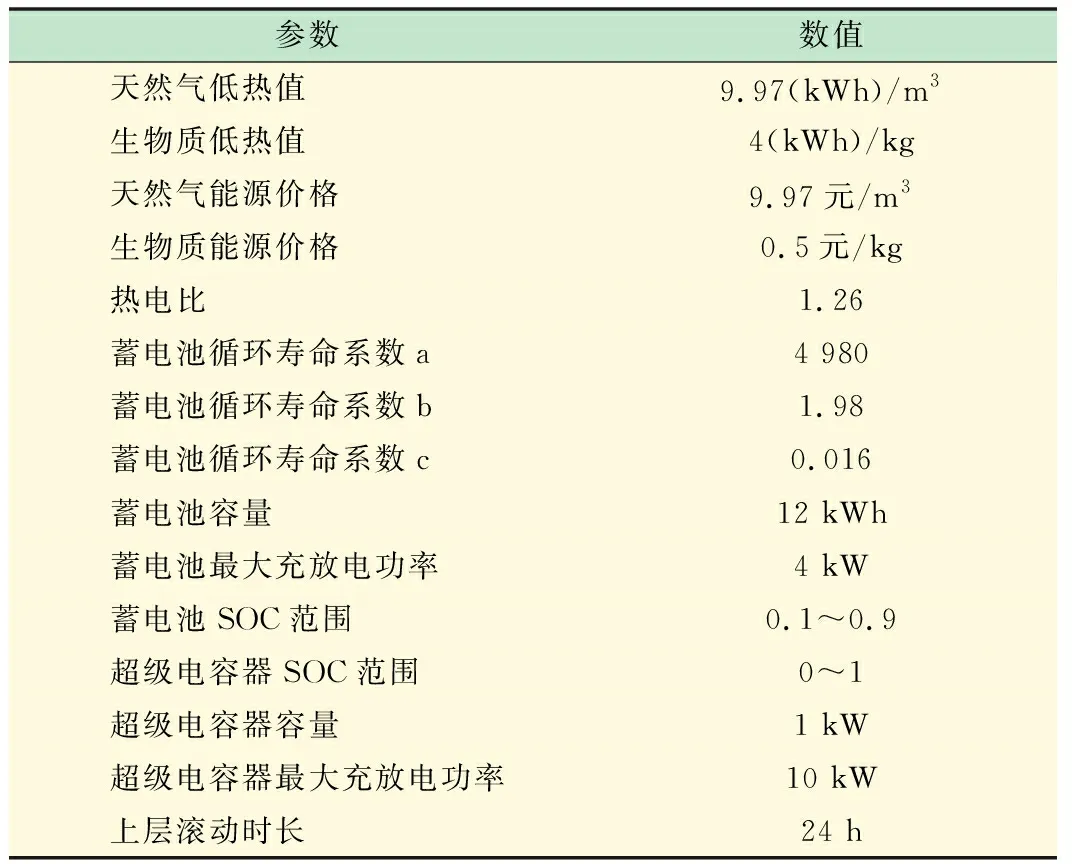
表A1 微电网的参数

(续表)

图A1 微电网热电预测负荷及风电、光伏出力

表A2 微电网系统交易电价
附录B
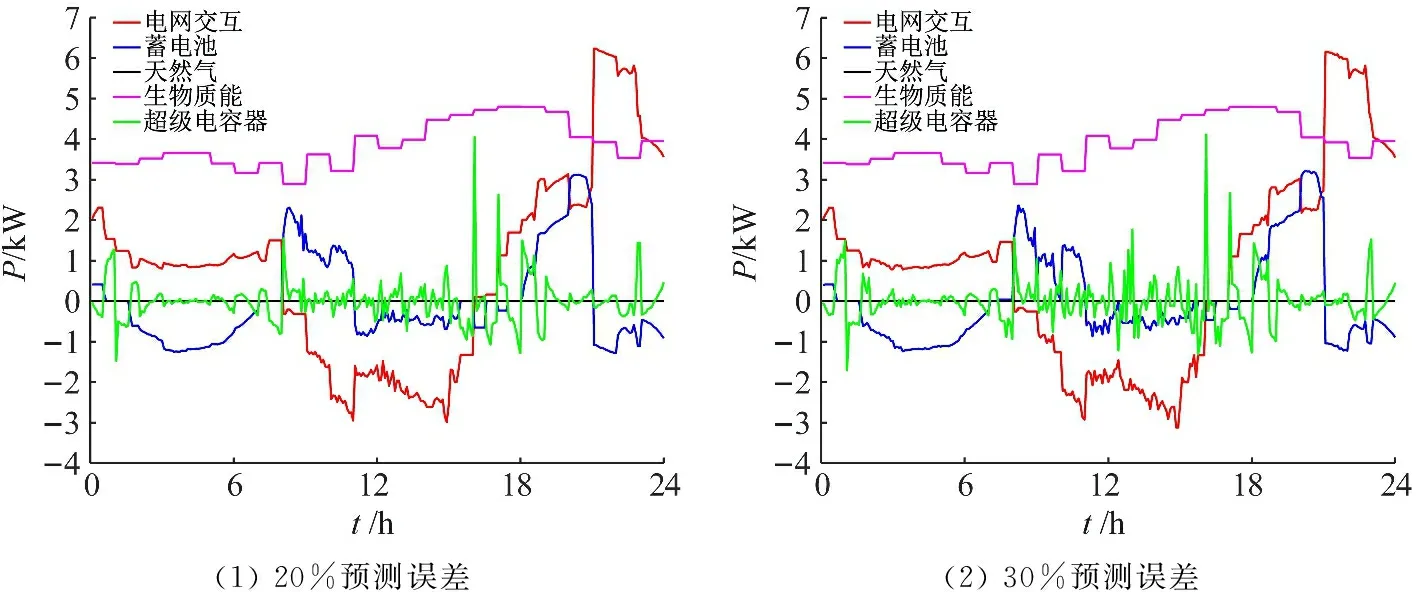
图B 不同预测误差下日内实时滚动调度结果
