基于变密度法的建筑机器人结构拓扑与能耗优化研究*

杨显龙 冯 伟 熊新红 王卫军 李道奇

1 武汉理工大学交通与物流工程学院 武汉 430063 2 中国科学院深圳先进技术研究院 深圳 518055

3 中国科学院大学 北京 100049

0 引言

随着建筑行业快速发展，传统的建筑业模式已逐渐无法满足需求，建筑业向智能化、信息化转型是必然的发展趋势[1，2]。建筑机器人相比常规的工业码垛机器人，建筑机器人有移动作业的需求，且机动性要求高，同时还需保证作业时建筑结构的承载安全[3]。所以，如何降低建筑机器人机体质量以及工作能耗是建筑机器人设计时应考虑的重要问题。目前，机器人的轻量化研究多基于轻质材料[4]及结构优化[5]等方面进行。

结构优化方法通常分为尺寸优化、形状优化和拓扑优化，其中拓扑优化有更高的设计自由度和设计空间[6]。因此，在轻量化设计时，对结构进行拓扑优化更具效率与价值。胡启国等[7]对RB08 工业机器人大臂进行拓扑优化，得到同时满足动态低阶频率最高和静态多工况条件下柔度最小的大臂优化结构；Bai Y F 等[8]使用基于Simp 的变密度法拓扑优化对SR-165 机器人上臂进行了轻量化设计，减重明显；陈继文等[9]对码垛机器人小臂进行拓扑优化，在保持原有力学性能的情况下，有效降低了机器人小臂质量；Ye D 等[10]提出了一种改进的结构优化方法，在保证机器人机架的刚度和振动性能下，完成机架轻量化设计；Liang M 等[11]对柔性关节工业机器人进行了拓扑优化，优化后的机器人手臂的阻力-载荷比和动力学性能得到了显著提高。

本文基于建筑工地中施工的实际需求，结合目前市面的工业码垛机器人，初步设计出一款移动式建筑材料搬运建筑机器人。以轻量化与能耗优化为目标，对机械臂整机及主要零部件进行静力学分析，对主要零部件进行拓扑优化与结构重新设计。通过对改进后的模型进行静力学分析，验证满足力学性能要求。最后对机械臂进行轨迹规划，并通过虚拟样机仿真实验，分析优化前后机械臂能耗情况，确认优化设计合理，达到设计目标。

1 建筑机器人整体结构设计

根据建筑工地实际工作状况，移动式建筑机器人设计采用机器人搬运为主、操作人员辅助定位的方案，机器人结构采用机械臂加移动设备的整体设计方案。

六自由度串联机器人具有工作范围大、性能灵活的特点。本文所述建筑机器人机械臂部分基于六自由度串联机器人设计，机器人的6 个关节分别控制搬运物料的空间位置和姿态。移动设备选用履带小车，并增加液压支腿，保证物料搬运时的设备稳定性。机器人总体结构如图1 所示。

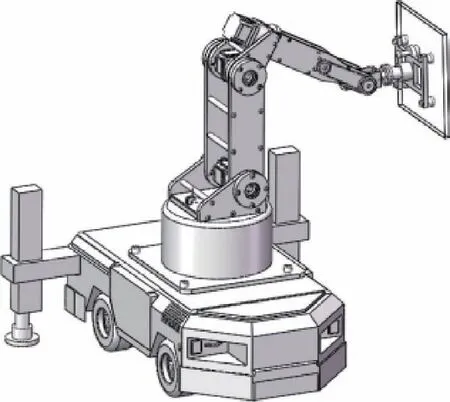
图1 建筑机器人总体图

机械臂的末端执行器为吸盘吸附装置，可用于表面光滑的建筑材料的搬运和安装，该建筑机器人主要应用于玻璃幕墙的搬运。常规幕墙的最大尺寸为1 936 mmh 1 184 mm，厚度为6 mm，玻璃的密度为2.56 g/cm3，常规情况单次搬运安装的质量为35.2 kg。

考虑吸附装置等执行器的附加负载，机械臂末端法兰盘有效负载设计为60 kg。从机械臂底座至末端法兰盘，6 个关节编号依次为关节1 ～关节6，设计并列出机械臂的主要参数如表1 所示。

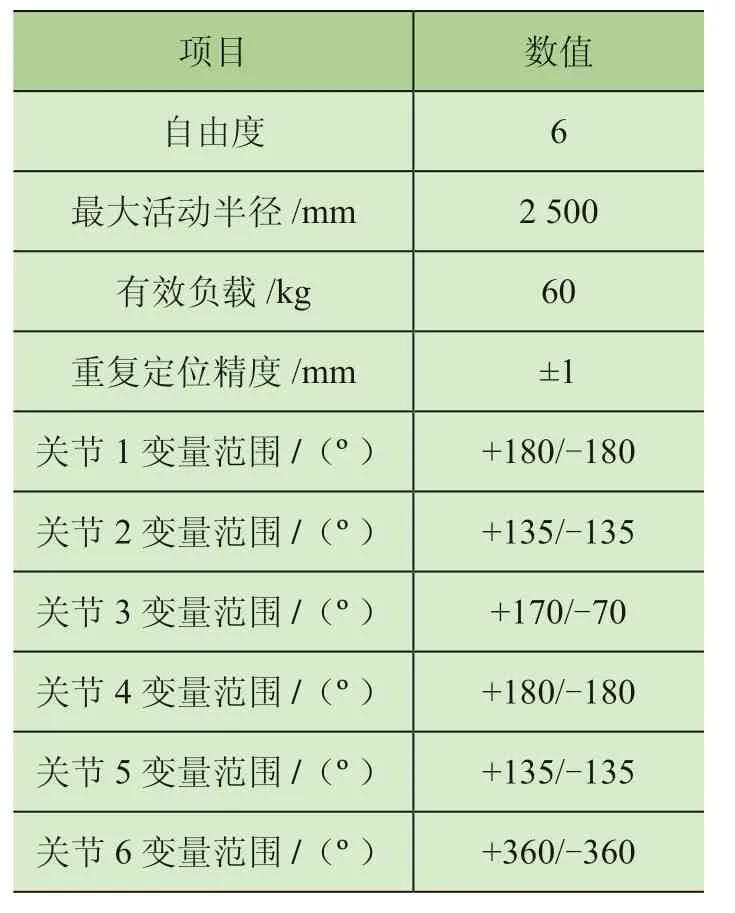
表1 机械臂主要技术参数

2 原始机械臂静强度校核

建立机械臂相应的三维模型，将简化模型导入Ansys Workbench 软件。其中机身材料选用6061 铝合金，密度为2.77 g/cm3，泊松比为0.330，弹性模量为69.6 GPa。当机械臂处于水平完全伸展姿态时，各部件达到最恶劣状态，此时末端变形量为最大值。考虑机械臂工作过程中风力、摩擦、瞬时加速度等因素的影响，在末端法兰盘施加900 N 竖直向下的力，以及全局标准重力加速度9.806 6 m/s2，约束机械臂底座的自由度。完成相应的材料参数设置、网格划分、边界条件建立后，创建分析任务，并提交计算。计算结果如图2、图3 所示。

图2 机械臂位移云图与等效应力云图

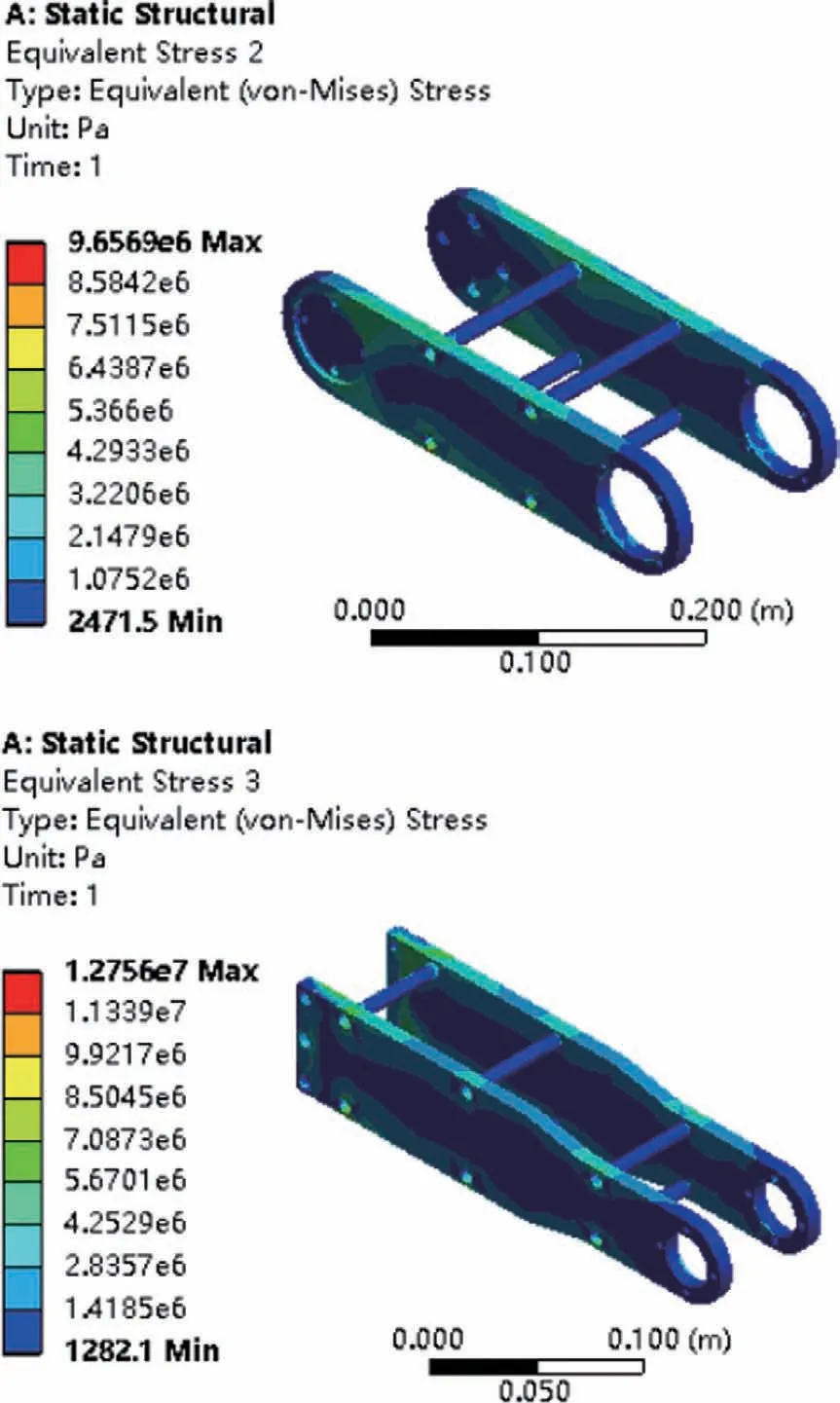
图3 大臂小臂等效应力云图

6061 铝合金的屈服强度为276 MPa，取材料的安全系数为2，许用应力为138 MPa。由分析结果可知，机械臂内最大等效应力为13.64 MPa，大臂、小臂承受的最大等效应力分别为9.65 MPa、12.76 MPa，结果均小于许用应力，满足强度要求。机械臂的最大位移量为0.246 mm，大臂、小臂的位移量分别为0.064 mm、0.217 mm，满足精度要求，初步验证机械臂的结构设计合理。

3 机械臂主要零部件拓扑优化设计

3.1 拓扑优化

通过机械臂极限工况的静力学分析，可知机械臂存在较大优化空间，基于变密度法对占重较高的大臂、小臂部分进行拓扑优化。 变密度法基于模型中每个元素的密度进行优化，将结构的拓扑优化问题转化为单元材料的最优分布问题。其中，采用固体各向同性材料惩罚模型（SIMP），引入插值惩罚因子以抑制中间密度，将密度值限定在0 或1，而非连续变化。剔除密度值为0 的单元，保留密度值为1 的单元，以实现材料的删减，数学模型式为

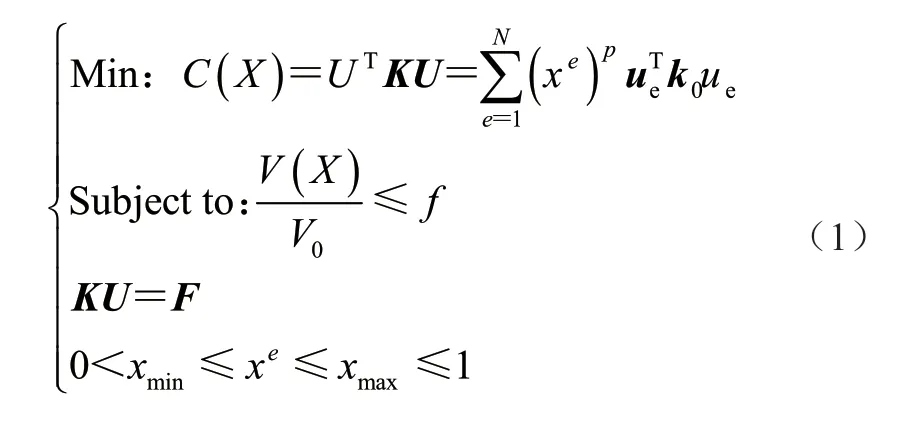
式中：X 为设计变量；xe为单元设计变量；C（X）为结构柔顺度；F 为载荷矩阵；U 为位移矩阵；K 为整体刚度矩阵；ueT为单元位移矩阵；k0为单元刚度矩阵；V（X）为设计变量状态下结构有效体积；V0为在设计变量取1 状态下的结构有效体积；f 为体积优化系数；p为惩罚因子，取p ＞0。

3.2 优化结果与模型设计

将机械臂整体静力学分析计算结果导入Ansys Workbench 软件中，采用变密度法对机械臂的大臂和小臂部分进行拓扑优化。根据大臂与小臂的优化空间情况，设定优化目标整体保留材料体积占比40%，多次迭代计算后结果如图4 所示。

图4 大臂、小臂拓扑优化计算结果图

基于优化计算结果，同时考虑加工难度，对大臂和小臂结构进行修正建模及重新设计，改进后的大臂与小臂结构如图5 所示。

图5 优化后大臂、小臂结构图

对于重新优化设计的机械臂，通过去除材料可使大臂、小臂的质量明显减轻，优化设计前后大臂、小臂的质量对比如表2 所示。

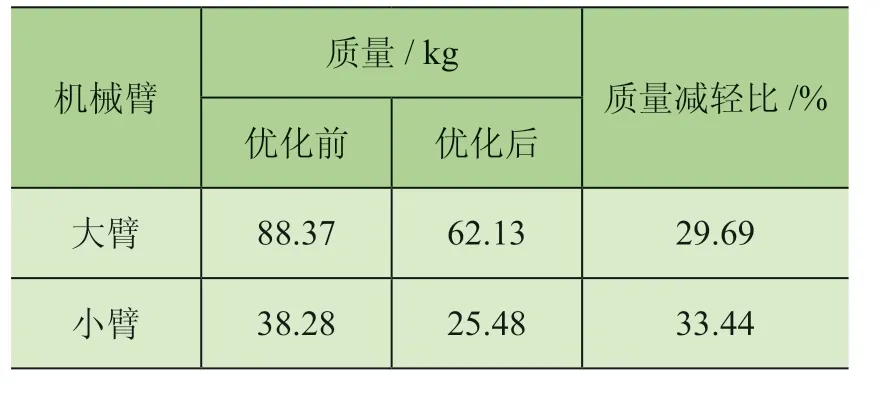
表2 机械臂优化前后质量对比

4 改进后机械臂静力学分析

将优化后的机械臂导入到Ansys Workbench 软件中，在同样的极限工况下进行静力学分析，设置与原始机械臂相同的材料参数、载荷以及约束条件等进行计算，其结果如图6、图7 所示。

由图6、图7 分析结果可知，优化设计后的机械臂内最大等效应力为13.35 MPa，大臂、小臂结构承受的最大等效应力分别为9.90 MPa、13.15 MPa。机械臂的最大位移量为0.252 mm，大臂、小臂结构的最大位移量分别为0.067 mm、0.223 mm，满足力学性能。机械臂优化前后性能对比如表3 所示。

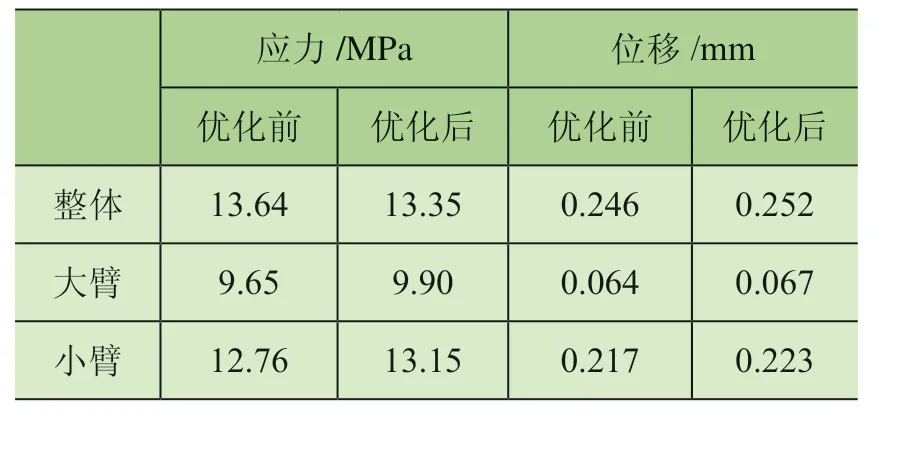
表3 机械臂优化前后性能对比

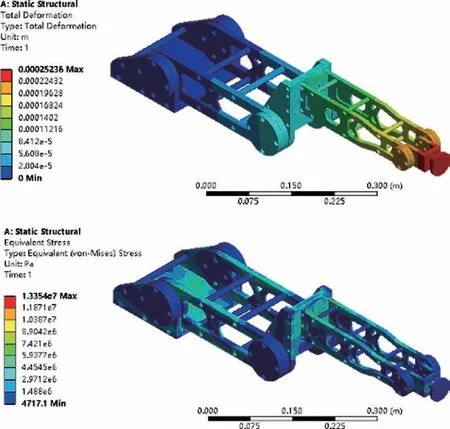
图6 优化后机械臂位移云图与等效应力云图

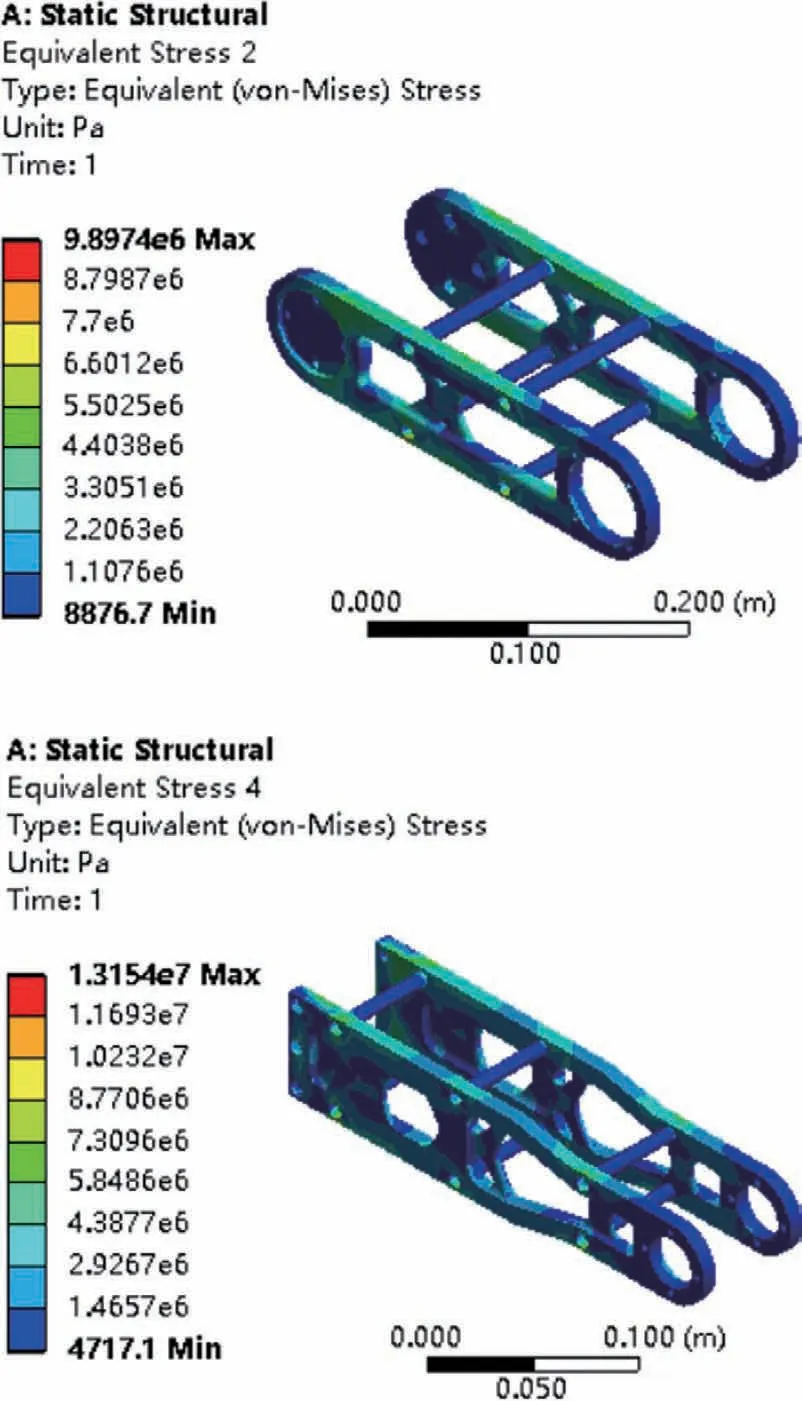
图7 优化后大臂小臂等效应力云图

5 动力学仿真实验

优化后的复杂结构难以使用常规的动力学建模方法进行研究，可采用虚拟样机技术，利用ADAMS 软件对优化前后的机械臂进行动力学仿真分析，以研究优化前后机械臂工作能耗情况。分别将模型导入至ADAMS 中，并设定相关参数，如图8 所示。

图8 ADAMS 动力学仿真模型

使用基于关节空间的方法，对机械臂各关节运动开始与结束的角度θ0与θ1、角速度以及角加速度设置约束，利用五次多项式插值分析法，实现对机械臂末端执行器的轨迹规划，可得到指定约束条件下关节1 ～关节4 的角度、角速度、角加速度随时间变化的函数，即

设运动结束时间为t1，根据约束条件求解得

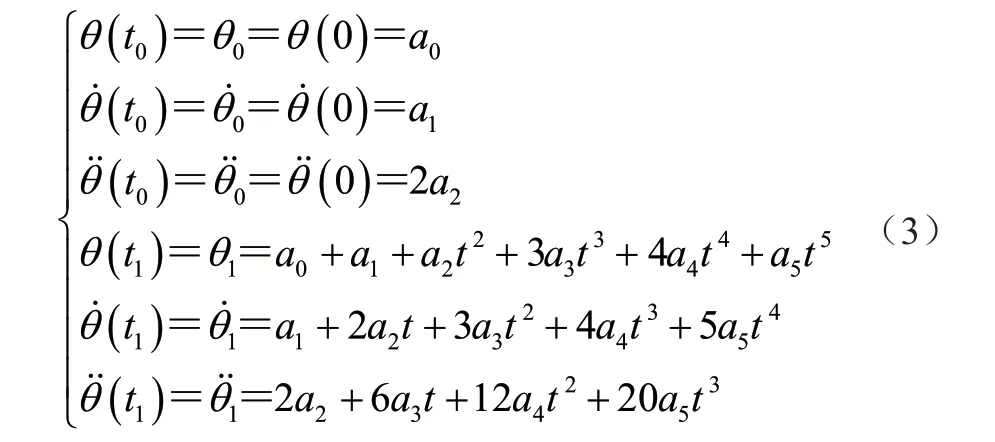
将Motion驱动函数设置为所求的关节角变化函数，进行动力学仿真分析。其中，关节2、关节3 承受较大扭矩，故选取关节2、关节3 电动机功率峰值作为机械臂能耗的优化指标，迭代计算后关节2、关节3 电动机功率变化曲线如图9 所示。

由图9 可知，优化设计后的机械臂在抬升手臂达到相同位姿时，对比优化前，关节2、关节3 的电动机功率峰值与整体变化曲线有明显的下降。

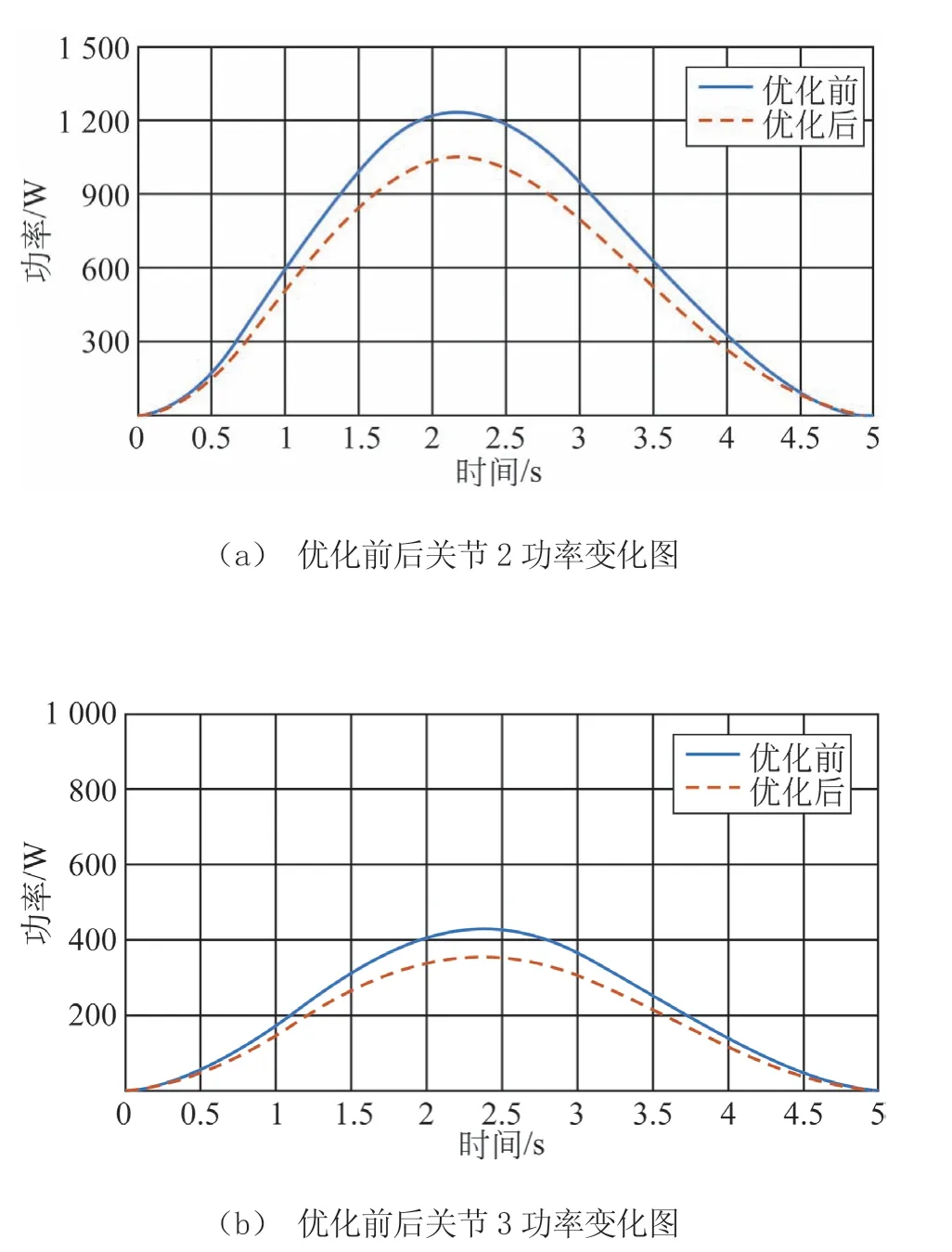
图9 优化前后关节电动机功率曲线图

6 结论

本文设计了一款移动式建筑机器人整体结构方案，使用变密度法对机械臂大臂、小臂进行结构拓扑优化，优化后大臂质量降低29.69%，小臂质量减轻33.44%，实现了轻量化目标。通过对机械臂进行轨迹规划以及设计、进行动力学仿真实验，得知优化后的机械臂能耗得到明显改善。研究思路与结果可为建筑机器人等移动式物料搬运机器人的新产品研发提供技术支持。