起重机攀爬机器人运动学分析与仿真*
2022-08-04赵章焰
赵章焰 秦 烺
武汉理工大学交通与物流工程学院 武汉 430063
0 引言
起重机械是用于港口码头装卸货物的主要设备,随着工作年限的增加会出现裂痕、生锈或表面污渍等现象,故需定期检查与清洁。传统的检查与清洁方式是由工作人员在起重机各表面完成任务,危险程度高,且效率较低。采用攀爬机器人来代替工人完成工作,可以极大地提高工人的安全保障以及工作效率[1]。因此,设计一款轮腿结合式的攀爬机器人,由4 条支腿和4 个车轮协同工作,在平坦的壁面攀爬时采用车轮运行的方式,跨越障碍和过壁面棱角时采用支腿运行的方式。不仅可避免轮式机器人的越障困难问题,还能提高足式机器人的运行平稳性和运行速度[2]。
针对机器人的越障性能,本文使用Matlab 对轮腿结合式机器人进行越障过程的运动学分析,研究机器人支腿在运动过程中的轨迹、速度、加速度等运动特征,采用改进的D-H 参数建立模型[3],运用解析法计算出运动学逆解的各关节的关节角[4],最后通过Matlab 机器人工具箱完成支腿越障的运动学仿真分析,进而研究攀爬机器人的运动特点[5]。
1 攀爬机器人的运动学分析
攀爬机器人的整体结构是一个4 轮小车,车体与车轮之间通过支腿连接,支腿由多个关节轴和连杆组成,机器人支腿三维模型如图1 所示。在研究支腿的运动学时,设所有构件均为刚体,仅考虑各杆件之间的运动关系,不考虑各杆件及构件之间的力学因素,忽略关节受弹性、摩擦、迟缓和间隙的影响。
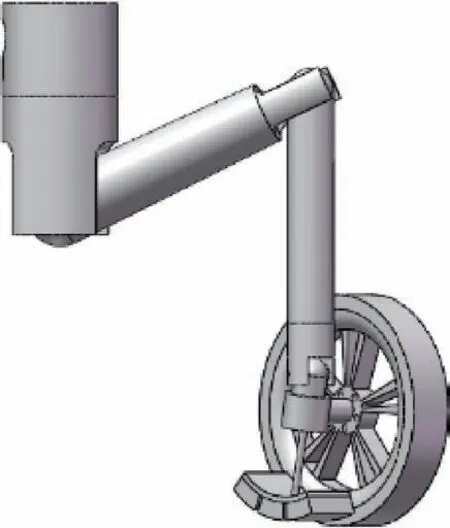
图1 攀爬机器人支腿三维模型
1.1 建立机器人支腿坐标系
攀爬机器人的支腿由5 个关节串联组成,可在三维空间中实现5 个旋转自由度的运动。通过关节角θi、连杆偏距di、关节偏移ai和连杆扭转角αi等参数来描述相邻2 连杆之间的相对空间位置关系。运用改进的Denavit-Hartenber 参数法(简称D-H 参数法),建立机器人支腿关节的空间坐标系,进而构建出整个机器人的空间结构模型。机器人支腿的参数如表1 所示。
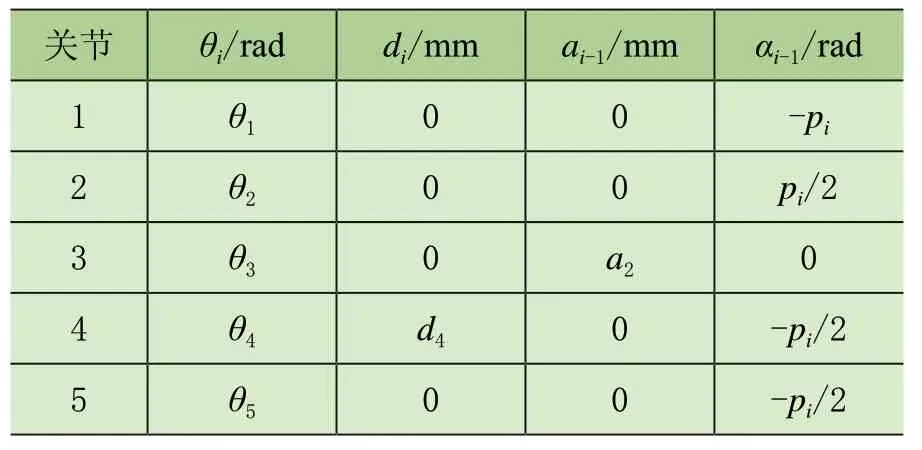
表1 机器人的D-H 参数表
采用D-H 参数法建立机器人支腿运动学模型,设连杆i 相对于连杆i-1 坐标系的位姿表达式为i-1iT,则连杆i 相对于基座标系的位姿表达式为
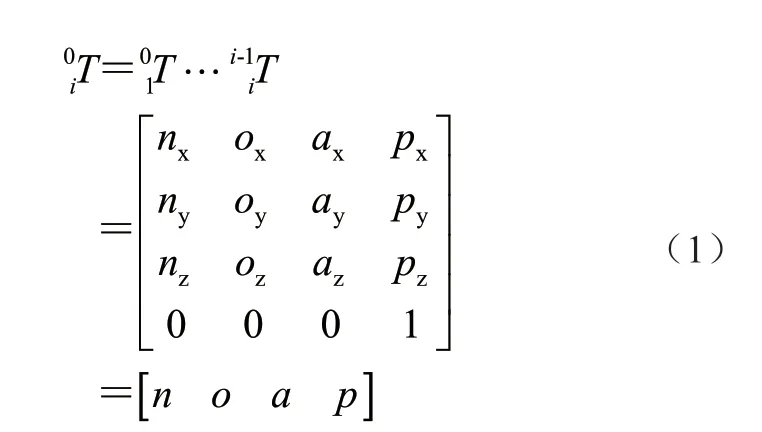
式中:[n o a]为姿态向量,P 为位置向量。
1.2 运动学正解
给机器人的支腿每个关节指定各自的关节坐标系,再确定从一个关节到其相邻关节坐标系间的变换矩阵,在已知各关节的转角后即可求解出支腿末端的位姿,从而建立出机器人的运动学方程。
将机器人连杆的4 个参数代入到广义变换矩阵中,即可得到相邻2 杆件之间的位姿变换矩阵。相邻2 连杆之间的广义变换矩阵为
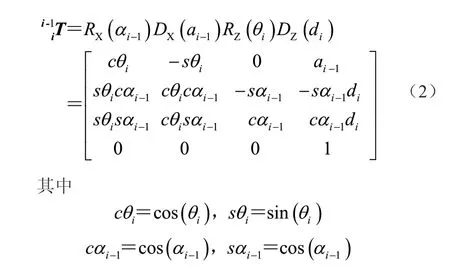
将各关节的4 个参数代入上述广义变换矩阵中即可得到相邻2 杆件之间的位姿变换矩阵,记为所以攀爬机器人的支腿末端位姿的变换矩阵可表示为
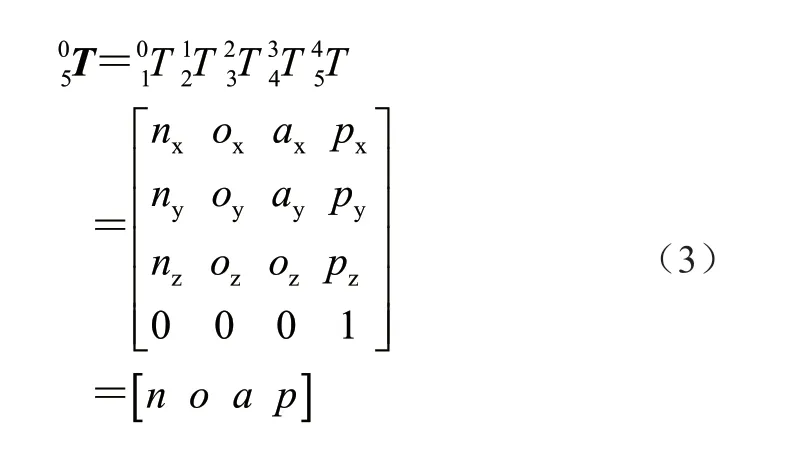
上述变换矩阵的公式中变量只有θi,当已知各关节的关节角θi时,即可求解出各相邻杆件间的相对位姿坐标以及末端执行器相对于基座标系的位姿坐标,通过上式计算可得变换矩阵中表示姿态和位置向量对应元素的值分别为

1.3 运动学逆解
机器人在实际运动过程中,通常已知一个末端工作位置,然后按照某个设定的轨迹运动到目标位置,从而完成相应的工作。所以,当已知攀爬机器人支腿末端相对于基座标的姿态和位置05T 后,即可通过运动学逆解代数求解出各关节的关节角θ 值。通过矩阵计算机器人的逆解,分别可得出5 个关节的求解过程。
由式(3)计算出矩阵中各元素的值为
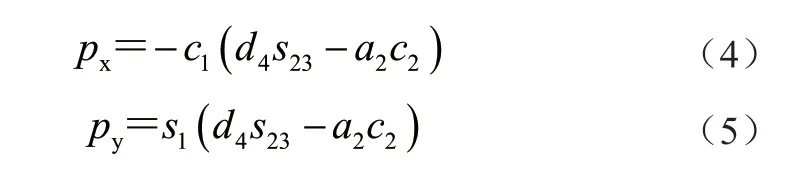
由式(4)和(5)计算可得

通过式(3)得到变换矩阵为

方程(7)两边矩阵(1,4)、(3,4)对应位置元素相等可得

对式(8)、式(9)进行化简计算,消除包含有θ3的项,得到

由上述运动学逆解计算结果可知,θ2有2 个解,而在机器人实际运动过程中,由于周围环境或自身体积形状会对机器人的工作空间有限制,并不是所有的解都是有效解,故应根据实际的工作情况来验证所求的运动学逆解是否合理。
2 机器人工作域
在运动学分析时,要考虑机器人的实际工作范围,取攀爬机器人支腿末端所能到达的三维空间所有点的集合,该集合即为其工作域。在研究机器人工作域时,不考虑机器人支腿的姿态,而只研究其位置,所用数学公式只与位置向量P 有关,即
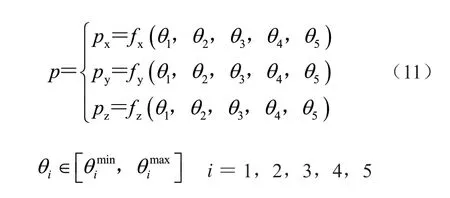
式中:p 为工作域,θi为各关节变量,分别为第i 个关节变量的最小值和最大值。
由于工作环境、机器人自身结构以及构件间的相对配合等条件会对各关节的活动范围有约束,所以θi的取值是一个范围,在最大值和最小值之间不可取任意值。在进行机器人工作域的求解时可采用蒙特卡洛法[6],蒙特卡洛法是一种以概率和统计理论方法为基础的随机模拟方法[7]。首先通过运动学正解的变换矩阵可得机器人末端点的位置向量,即
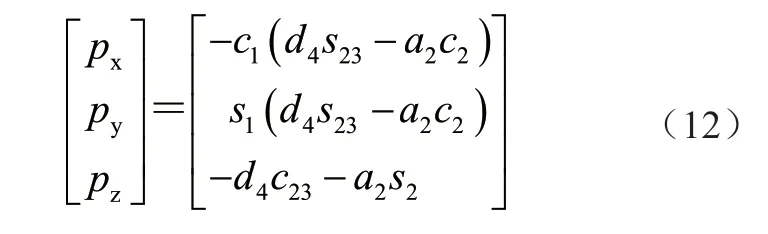
根据实际工作情况确定各关节角的取值范围,然后调用Matlab 中的Rand 函数对关节变量在取值区间内进行随机取值,最大关节变量值与最小关节变量值的差乘以Rand 函数再加上最小值,每进行一次计算就随机产生一个关节变量θi,即

将5 个关节变量对应的最大值和最小值分别代入对应关节角的计算公式中,并赋予a2、d4对应的数值,然后使用循环命令设置生成关节变量角的次数,每执行一次循环命令即输出一个末端点,通过Matlab 编写程序完成该算法,输出表示机器人工作域的点集图形。
根据攀爬机器人的实际工况代入参数数值a2=100 mm,d4=100 mm,代入各关节变量θi的取值范围边界值为分别θ1=[-pi/2,pi/2]、θ2=[-pi/4,pi/2]、θ3=[-3pi/4,pi/4]、θ4=[-pi/2,pi/2]、θ5=[-3pi/4,3pi/4]。设置循环次数为100 000 次,即可随机生成100 000 个点位,由这些点位组成的集合即机器人支腿末端可达到的工作区域,通过调用Matlab 的Plot3 绘图命令,仿真输出代表机器人支腿工作域的三维空间点集云图,如图2 所示。
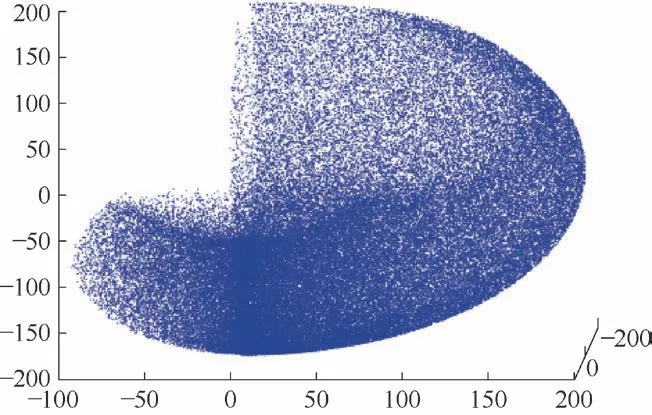
图2 三维空间点集云图
由图2 可知,攀爬机器人支腿末端所能到达的工作区域与Matlab 仿真所得到的三维空间点集云图尺寸大小以及点位分布相对应,图中下方点的分布比较密集,由于支腿末端多是与攀爬壁面相接触,故实际上机器人支腿末端大多也是在相对位置的下方。中间部分由于2相邻连杆的长度相同导致中间一部分区域支腿末端无法到达,故形成了无点区域。左侧空白部分没有点位,因为左侧为机器人车体部分,机器人的支腿只能在机器人车体外侧以及下侧部分区域活动。仿真结果点位云图与机器人实际工作区域相一致,符合攀爬机器人的正常工作要求。
3 攀爬机器人支腿轨迹规划
3.1 支腿模型建立
机器人在使用支腿进行前进运动时有2 种状态:1)支腿足端运动状态,包括支腿位姿调整,支腿抬高进行越障;2)支腿足端不动而车体运动的状态,主要是用于越障时改变机器人车身高度和位置,以便后续的支腿越障行为。
使用Matlab 中的Robotics Toolbox 工具箱对攀爬机器人的支腿进行三维建模[8],通过Link 函数以及关节参数θ、d、a、α 来创建5 个连杆,调用SerialLink 函数连接5 个连杆组成一条运动链[9],生成的机器人支腿模型如图3 所示。
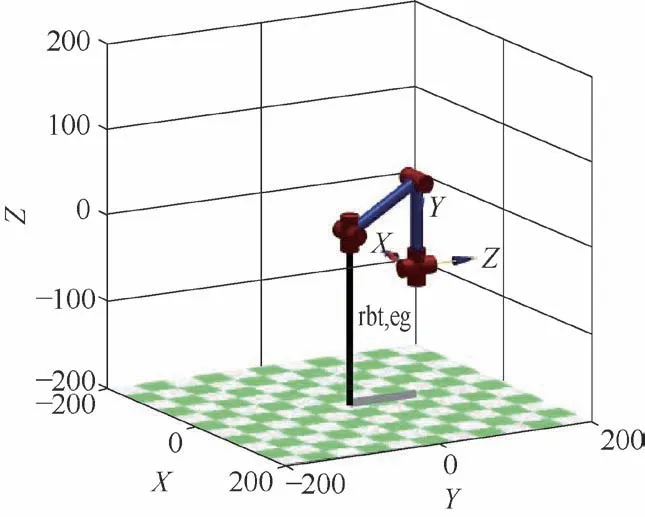
图3 机器人支腿模型
3.2 轨迹规划仿真
机器人支腿末端从起始点运动到终止点有许多条路径,要在这些路径中选择出一条速度和时间都最优的路径,本文采用五次多项式插值算法进行计算[10],为了让机器人的运动更加平稳,需要在起始点和终止点之间添加几个中间路径点用于过渡。将关节角之间的变换看成关于时间的函数θ(t),该函数从起始点开始依次通过个中间点最后到达终止点,可表示为
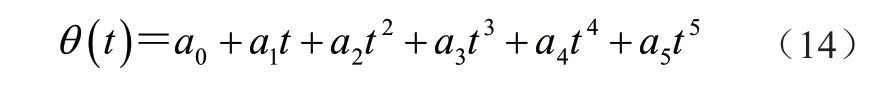
调用Robotics Toolbox 工具箱中的Jtraj 函数,Jtraj函数用于在关节空间下机器人2 个不同位行间各关节角度变化差值拟合生成轨迹,调用格式为

式中:qs为初始关节角度,qe为终止关节角度,t表示此过程包含的时间步数,每个时间步对应一个瞬时位行。Q、qd、qdd分别为关节角的角位移、角速度和角加速度。
Jtraj 函数利用五次多项式进行插值规划轨迹[11],默认初始时和终止时关节的速度和加速度的值均为零。
由于机器人的4 个支腿越障时的轨迹相同,本文将研究一条支腿跨越障碍时的轨迹规划仿真,支腿在越障时的动作可分为4 步:1)支腿抬高脱离壁面;2)支腿关节转动调整位置使支腿越过障碍物;3)调节支腿末端点姿态,使车轮方向保持继续向前;4)降低支腿高度,与工作面接触,完成越障。
支腿越障初始位置的各关节角qs1和终止位置的各关节角qe1分别为
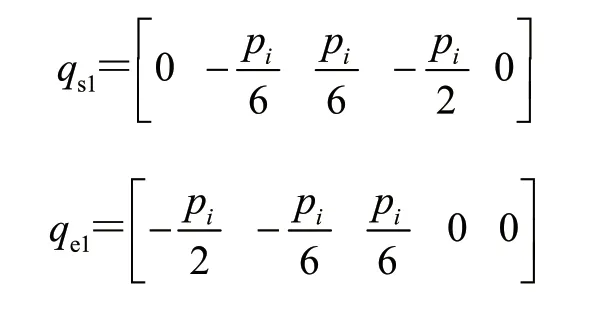
为了使机器人工作时的轨迹平稳过渡,在初始位置与终止位置之间添加3 个中间路径点。每2 个路径点之间设置采样时间为2 s,总时长为8 s,步长为0.05 s,机器人支腿的末端轨迹图如图4 所示。

图4 位姿调整时机器人支腿末端轨迹
在支腿位姿调整的过程中,主要运动关节为关节1和关节2,调用Matlab 机器人工具箱中的Plot 函数,对采用5 次多项式插值的计算的轨迹结果绘制图形,得到各关节的角位移、加速度和角加速度随时间变化的曲线图,分别如图5 ~图7 所示。
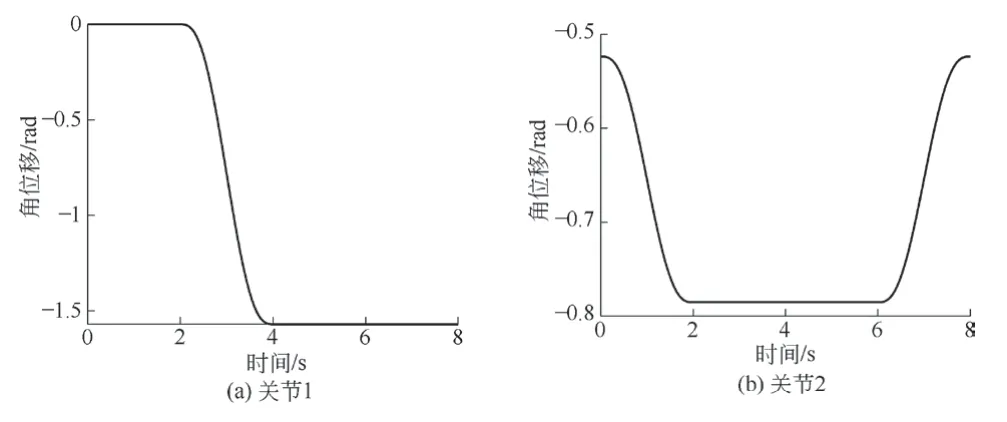
图5 越障时关节1、关节2 角位移曲线

图6 越障时关节1、关节2 角速度曲线

图7 越障时关节1、2 角加速度曲线
由图5 ~图7 曲线可知,关节1 和关节2 的位移、速度和加速度曲线光滑平稳,且相互对应;在起始和终止位置速度为0,且位移不再发生变化,加速度的正负与速度的增大减小相对应。因此,越过障碍的轨迹规划合理,该动作可以正常运行。
4 结论
1)针对用于大型金属结构的监测平台,设计了一款轮腿结合式的攀爬机器人,通过对机器人采用支腿越障的过程进行了运动学分析,合理安排机器人运动过程中的位姿,保证支腿运动的精度和效率,为后续的动力学、控制算法以及运动规划分析奠定理论基础。
2)在正、逆运动学分析的基础上运用蒙特卡洛法对机器人的支腿工作域进行三维仿真分析。结果表明,支腿的工作空间范围充足,能满足支腿越障和过棱边时的各种动作要求。
3)采用Matlab 中的机器人工具箱,对机器人越障的过程进行轨迹规划。结果表明,机器人在越障运动中的角位移、角速度和角加速度曲线光滑平稳,未出现突变和间断现象,说明机器人能够安稳地跨越障碍。
