基于相场法的沉管隧道结构损伤区识别
2022-08-03李宏哲那通兴
王 野,李宏哲,那通兴
(1.中交第二航务工程局有限公司,湖北 武汉 430040; 2.中交公路规划设计院有限公司,北京 100088)
0 引言
沉管隧道作为城市水下通道、跨江跨海通道修建的重要工法,具有诸多优点,比如施工周期短、施工质量和安全有保障、隧道截面灵活、对地质环境影响小等。因此,在各国的隧道建设中得到了广泛的应用[1-3]。然而,沉管管段体积大且由不同的组分浇筑而成,在浇注过程中具有天然的自身损伤。同时在沉管施工过程中,由于水土压力作用[4]、额外的锚固力甚至偶发的沉船荷载等,可能使沉管管节发生次生的损伤破坏,因此对沉管结构的损伤识别和预测是一个重要的研究课题。
国内外针对沉管隧道结构的受力特性及损伤演化的研究已取得了诸多进展。例如,张苑竹等[5]基于舟山海底隧道,分析了沉管管节在预制过程中产生的温度和应力。王湛等[6]考虑不均匀地基刚度影响,对沉管隧道的损伤进行了分析。赵天驰等[7]考虑地基刚度不均匀的影响,进行了沉管隧道接头变形分析。甘鹏山等[8]初步探索了沉管隧道横向地基刚度分布。胡指南等[9]针对沉管隧道节段接头剪力键破坏状态与机理展开了研究。丁文其等[10]建立了基于三维地层-结构法的沉管隧道数值模型。王伟强等[11]通过数值模拟和室内试验研究了GINA止水带力学性能。魏纲等[12-13]针对沉管隧道管节柔性接头模型开展研究,并考虑了临时垫块支撑对沉管隧道结构受力的影响。陈富强等[14]开展了沉管隧道节段接头混凝土剪力键与摩擦力协同抗剪机理试验。陈红娟等[15]建立了基于有限元-无限元的沉管隧道三维动力数值模型。然而,目前的这些研究不能很好地描述沉管隧道结构中损伤区的扩展及断裂区域的形成,且针对这个问题也没有强力的数值模拟工具。
基于目前研究存在的不足,本研究将目前研究断裂问题的相场法[16-18]引入沉管隧道领域,用相场法来对沉管隧道结构的损伤断裂区进行识别。具体地,以襄阳市某沉管隧道为例,采用谱分解相场法,建立二维相场分析模型,对该沉管隧道的结构损伤断裂区进行识别,研究沉管施工期的结构损伤的可能分布及水位、覆盖层和沉管结构能量释放率对损伤区的影响,以期为谱分解相场法识别沉管隧道结构损伤断裂区这一研究方向提供新的研究基础,为沉管工程的施工和运营安全提供新的思路。
1 多场耦合相场方法
格里菲斯脆性断裂理论[17]表明,当弹性体Ω储存的弹性能超过自身断裂阻抗时,弹性体发生断裂,裂纹开始萌生和扩展。因此,对于准静态过程,裂纹扩展问题可归结为自由能泛函的最小值问题:
(1)
式中,L为自由能泛函数;ψε(ε)为弹性能密度;ε为应变张量;Gc为临界能量释放率;u为任意点x的位移;b和f分别为作用于弹性体上的体力和面力;S为弹性体表面;∂Ωh为弹性体外力作用边界;Γ为弹性体内部的不连续断裂面。
相场法是格里菲斯脆性断裂理论的扩展,该法采用一个额外的标量场(相场)替代尖锐裂纹[17]。相场与损伤的概念接近,在裂纹面附近具有连续变化的位移梯度,因此在本研究中可用来进行断裂和损伤的识别。定义相场φ范围为[0,1],其中φ=0代表材料处在无损伤状态,而φ=1则代表材料处在完全破坏状态[16]。采用各向异性相场法中最典型的谱分解相场法,该方法将应变进行拉压分解,认为只有拉应变引起裂纹扩展,进而构建只有拉应变参与的相场演化驱动力[16]。求解损伤区的控制方程为:
(2)
式中,σji为柯西应力张量σ的分量;xi为位置坐标;bI为体力分量;l0为尺度参数,控制着相场过渡区宽度,表征相场的弥散程度,可近似代表裂缝宽度,l0越小,相场代表的裂纹越细且更接近尖锐裂缝;0 这样,应用谱分解相场法求解弹性体的断裂损伤区域即是对式(2)所示的耦合方程组进行求解,弹性体的损伤断裂演化通过式(2)的相场演化方程进行求解。因此,相场模型问题本质上为多场耦合问题。 采用有限元方法求解式(2),根据有限元弱形式及对位移场和相场的离散,式(2)的控制方程可改写为: (3) (4) 采用分步解耦方法求解式(3)和式(4),具体步骤如下:(1)在某个时间步,根据之前求解结果,预估相应的位移场和相场。(2)先固定相场,对式(3)进行求解,获得位移场。(3)根据获得的位移场,对历史场进行更新,然后将H代入式(4),重新求解相场。(4)计算新求解得到的相场与相场预估值之间的误差,如果相对误差小于容许值,则该时间步计算结束。(5)如果误差较大,则将相场预估值更新为新求解得到的相场值,然后重新计算(1)到(4)步,直到相对误差值满足要求。 采用含预制裂纹的受剪方板这一基准算例对所采用的相场方法及其实现手段进行验证。该算例已被诸多学者如Miehe等[17]以及Hesch等[18]进行了广泛研究,算例的几何条件及边界条件如图1所示。计算采用的模型参数如下:拉梅常数μ=80.77 GPa,拉梅常数λ=121.15 GPa,临界能量释放率Gc=2 700 N/m,用于避免计算过程中出现奇异性而导致计算不收敛的k=10-9,尺度参数l0=7.5×10-3mm或l0=1.5×10-2mm。 图1 验证例子的几何模型和边界条件(单位: mm)Fig.1 Geometric model and boundary conditions of verification example (unit: mm) 采用双线性四边形单元对图1所示的方板进行有限元离散,同时限制单元最大尺寸不超过3.96×10-3mm。为兼顾计算效率和计算精度,计算采用非均匀加载步,即对于前80个时间步,每个位移加载步的位移增量为10-4mm,而对之后的所有加载步,每个位移加载步的位移增量为10-5mm。裂纹的最终扩展情况如图2所示,表明本研究计算结果与参考文献[16-18]计算得到的裂纹路径一致。另外,图2给出了不同尺寸参数时的荷载-位移曲线,这些曲线的数值与Hesch等[18]的计算结果一致,只在数值上有细微的不同。产生这种现象的原因为本研究和Hesch等[18]采用的算法不同。总之,图2的裂纹路径结果和荷载-位移曲线结果与文献结果一致,表明了本研究采用的模型及相应的算法是可行的,能够应用于对称沉管结构的损伤断裂分析。 图2 验证例子的裂纹形态和荷载-位移曲线Fig.2 Fracture patterns and load-displacement curves of verification example 以襄阳市某沉管隧道E5管节为例,建立二维相场分析模型,对该沉管隧道的结构损伤断裂区进行识别,研究沉管施工期的结构损伤的可能分布及水位、覆盖层和沉管结构能量释放率对损伤区的影响规律。 襄阳市某隧道是国内整体建设规模最大的内河沉管隧道,也是国内首例采用PPP+EPC模式实施的特长沉管隧道项目。隧道全长5.4 km,按时速60 km/h的双向6车道城市快速路标准设计,结构设计使用年限100 a,用2孔1管廊结构。其中鱼梁洲隧道东汊沉管段长660 m,起讫桩号K13+325~K13+985,采用(120.5×4+86.5×2) m长管节+5 m小节段的长度组合,管节断面总体外轮廓尺寸为:宽31.2 m×高9.2 m,如图3所示。 图3 鱼梁洲隧道东汊沉管管节标准横断面(单位:cm)Fig.3 Standard section of Dongcha immersed tube segment of Yuliangzhou Tunnel (unit: cm) 按图3所示的管节尺寸进行几何建模,管节结构设为均质体。采用的基准建模参数为:弹性模量为34.5 GPa,泊松比为0.2,临界能量释放率Gc=2 400 N/m,尺度参数l0=100 mm。采用三角形单元对几何模型进行离散,同时限制单元最大尺寸不超过50 mm。沉管结构上部施加竖向压力,两侧施加横向压力,底部固定法向位移,左侧角点同时固定水平位移用于消除刚体位移的影响。根据水土压力的受力特点,沉管两侧顶部连接段同时施加竖向压力和横向压力。 沉管受水土压力采用水土分算,模拟分2个过程: (1)沉管周围压力从0增加到水位为0时的水土压力、覆盖层压力和沉管抗浮锚固压力,土的浮重度按11 kN/m3计算,覆盖层厚度为5.287 m(根据E5管节的建设期河床高度计算),沉管抗浮锚固压力按42.4 kPa计算,根据计算中的非线性程度,此过程加载施加40个荷载步。 (2)在步骤(1)的基础上,增加水位并施加增加的水压力,直至计算到达设定水位,每个荷载步增加0.01 m水位。 针对施工期沉管周围压力从0增加到设定水土压力这一过程,数值模拟结果表明,不同施加压力对损伤区的分布影响很小,施加的压力只影响沉管损伤程度。图4给出了施加压力达到终值时的损伤区分布,表明沉管损伤区主要出现在左右隧道顶部内表面和中间隧道顶部外表面。损伤最大值出现在中间隧道顶部,为3.75×10-3。这些损伤区域为施工中需要着重关注的区域,必要时需要增加施工措施对该区域进行加固,而这些损伤区的分布与周围水土压力和锚固压力的相对大小及沉管结构的几何型式相关。施工期沉管损伤值远小于1,说明施工阶段沉管结构具有充足的安全储备。图5给出了不同压力加载率情况下对称沉管结构最大损伤的变化。可以看出,随着沉管周围压力的增加,损伤最大值也逐渐增加,从1.99×10-4增加到3.75×10-3,但损伤与压力加载率的关系并非线性;相反,当压力加载率增加时,损伤值增加的速率也增大。 图4 鱼梁洲隧道东汊沉管管节施工期损伤值分布Fig.4 Distribution of damage values of Dongcha immersed tube segment of Yuliangzhou Tunnel during construction 图5 不同压力加载率下施工期沉管损伤值Fig.5 Damage values of immersed tube during construction with different pressure loading rates 施工期结束后,沉管结构损伤与水位相关。在完成沉管上覆层及周围水土压力施加后,随着上覆层上水位的增加,沉管结构内应力场和位移场逐渐变化,沉管损伤区的分布及损伤大小受水位影响较大。E5管节正常水位高度为15.127 m,最小水位高度和最大水位高度分别为14.430 m和17.81 m。数值模拟结果表明,E5管节在3种不同水位情况下的损伤区域与图4类似,管节最大损伤值分别为0.03(正常水位)、0.028(最低水位)和0.038(最高水位)。沉管在正常运营阶段的损伤值很小,沉管隧道具有很好的安全储备。 为获得E5管节破坏的临界水位,不断增加水位使管节最大损伤值达到1且多场耦合计算不收敛(可认为管节破坏)。图6给出了临近破坏时沉管结构的损伤区分布。可以看出,沉管破坏的临界水位为67.171 m。另外,当水位为66 m时,中部隧道顶部损伤演化速率较左右2个隧道明显增大,因此沉管中部形成了2个明显的损伤集中区域,该区域的最大损伤值达到0.62。而当水位增加到67.15 m时,沉管中部的2个损伤集中带继续演化,在不断增加的水压作用下,应力在损伤区域逐渐集中,损伤最大值达到1,形成了2条对称的裂缝。 图6 鱼梁洲隧道东汊沉管管节水位增加损伤值分布Fig.6 Distribution of damage values of Dongcha immersed tunnel segment of Yuliangzhou Tunnel with different water levels 当水位继续增加时,应力在损伤区域继续集中。同时由于损伤加剧,造成了不同区域力学性质的改变,应力场重分布明显,沉管结构将出现多个损伤集中区域。当水位到达67.171 m时,中间隧道顶部的2条对称裂缝继续扩展。同时,左右2个隧道中部出现了从内表面向外表面扩展的竖向裂缝,左右两侧连接区域出现了从外表面向内表面扩展的斜向裂缝。这些裂缝和损伤区域的出现表明沉管结构已不满足安全性的要求,需要着重关注这些区域,并尽可能增加施工措施对这些区域进行加固处理。 对称沉管结构损伤最大值随水位变化的规律如图7所示。可以看出,随着沉管周围水位的增加,损伤最大值也逐渐增加,从3.75×10-3急剧增加到1。损伤最大值与水位呈非线性关系,随着水位的增加,损伤值演化速率也逐渐增加。造成这种趋势的主要原因为在相场法中,弹性能驱动着损伤区和裂缝的演化,而随着水压的增加,沉管结构内部应力增大并伴随着位移的增大。弹性能的增加是应力和位移的累积效应的结果,因此相场的增加速率与水位或者水压力呈非线性关系。 图7 不同水位下沉管损伤值Fig.7 Damage values of immersed tunnel under different water levels 在实际运营过程中,河床淤积和冲刷使E5管节上方覆盖土厚度发生变化,进而影响管节结构的损伤区分布。E5管节的河床最大回淤高程为+55.10 m(即管顶最大覆土厚度7.497 m),河床最大冲刷高程为+48.75 m(即管顶最小覆土厚度1.147 m),而管节的设计覆盖层厚度为5.287 m。因此,本研究在固定正常水位15.127 m的情况下,研究覆盖层厚度分别为1.147,5.287,7.497 m时沉管的损伤情况。模拟结果表明覆盖层厚度对损伤的分布没有影响,而只对损伤的量值产生影响。如图8所示,当覆盖层厚度增加时,沉管在施工期和正常水位情况的损伤均随之增大,但图8也表明实际运营中的河床淤积和冲刷所产生的影响很小,沉管管节的损伤值不超过0.035,E5沉管具有十分充足的安全储备。 图8 覆盖层厚度对沉管损伤值的影响Fig.8 Influence of coverage thickness on damage values of immersed tunnel 根据参考文献[16],临界能量释放率的选取可影响材料的抗拉裂能力,进而间接影响损伤区的影响范围及同等条件下的损伤程度。在实际工程中,由于沉管结构并非素混凝土,而是多种材料(如钢材)组成的混合材料,能量释放率的选取需进行室内试验确定或经验获取。本研究能量释放率的影响依据文献[16]的抗拉强度与能量释放率的转换关系及常规的沉管强度取得,考虑能量释放率分别为800,1 200,1 600,2 000,2 400 N/m时沉管隧道的损伤断裂情况。模拟结果表明,能量释放率不影响损伤分布,只影响损伤的数值大小,损伤值随能量释放率的增加而减小,即能量释放率越大损伤越不容易演化。不同临界能量释放率时沉管损伤区主要出现在左右隧道顶部内表面和中间隧道顶部外表面,同时损伤区最大值均出现在中间隧道顶部。 图9给出了不同临界能量释放率情况下第40个荷载步沉管结构的损伤最大值的变化。由于能量释放率越大,沉管结构抗裂性能越强,第40个荷载步时的最大损伤量随着能量释放率的增加逐渐减小且呈倒S型分布,即在1 200 N/m到2 000 N/m区间的变化较为平缓,而在其余区间变化较剧烈,特别是当能量释放率在2 400 N/m时沉管的损伤很小,几乎可以忽略不计。图10是不同临界能量释放率情况下沉管破坏时水位的变化情况。与图9不同的是,图10显示沉管破坏水位与临界能量释放率呈线性关系,临界能量释放率增加时,沉管能够承受更高的水位。这也与实际工程中采用更高强混凝土材料时沉管结构可承受更大水压的现场观察结果吻合。 图9 不同能量释放率时第40个荷载步沉管损伤Fig.9 Damage of immersed tunnel for the 40th load step with different energy release rates 图10 不同能量释放率时沉管破坏水位Fig.10 Water level of failure of immersed tube with different energy release rates 以襄阳市某沉管E5管节为例,建立了二维相场分析模型,对沉管隧道的结构损伤断裂区进行了识别,得到如下结论: (1)施工时沉管损伤区主要出现在左右隧道顶部内表面和中间隧道顶部外表面,同时损伤区最大值出现在中间隧道顶部。随着沉管周围压力的增加,沉管损伤最大值也逐渐增加。本项目施工期沉管总体损伤较小,E5沉管最大损伤值不超过0.04。 (2)当水位增加到沉管破坏时,中间隧道顶部有2条对称裂缝继,左右2个隧道中部出现从内表面向外表面扩展的竖向裂缝,左右两侧连接区域出现从外表面向内表面扩展的斜向裂缝。 (3)沉管破坏水位与临界能量释放率呈线性关系,临界能量释放率增加时,沉管能够承受更高的水位。 (4)运营期覆盖层厚度和水位增加造成沉管损伤最大值逐渐增大,但沉管结构仍具有充足的安全储备。 (5)本研究有助于进一步完善沉管隧道安全性能分析模型,为沉管工程提供新的数值方法与工具,能够对沉管隧道在施工以及运营中的高度损伤或断裂破坏区域进行直观的识别和精准刻画,为施工中抗裂措施的施加提供参考。2 相场模型的有限元求解
2.1 分步解耦法

2.2 相场模型验证
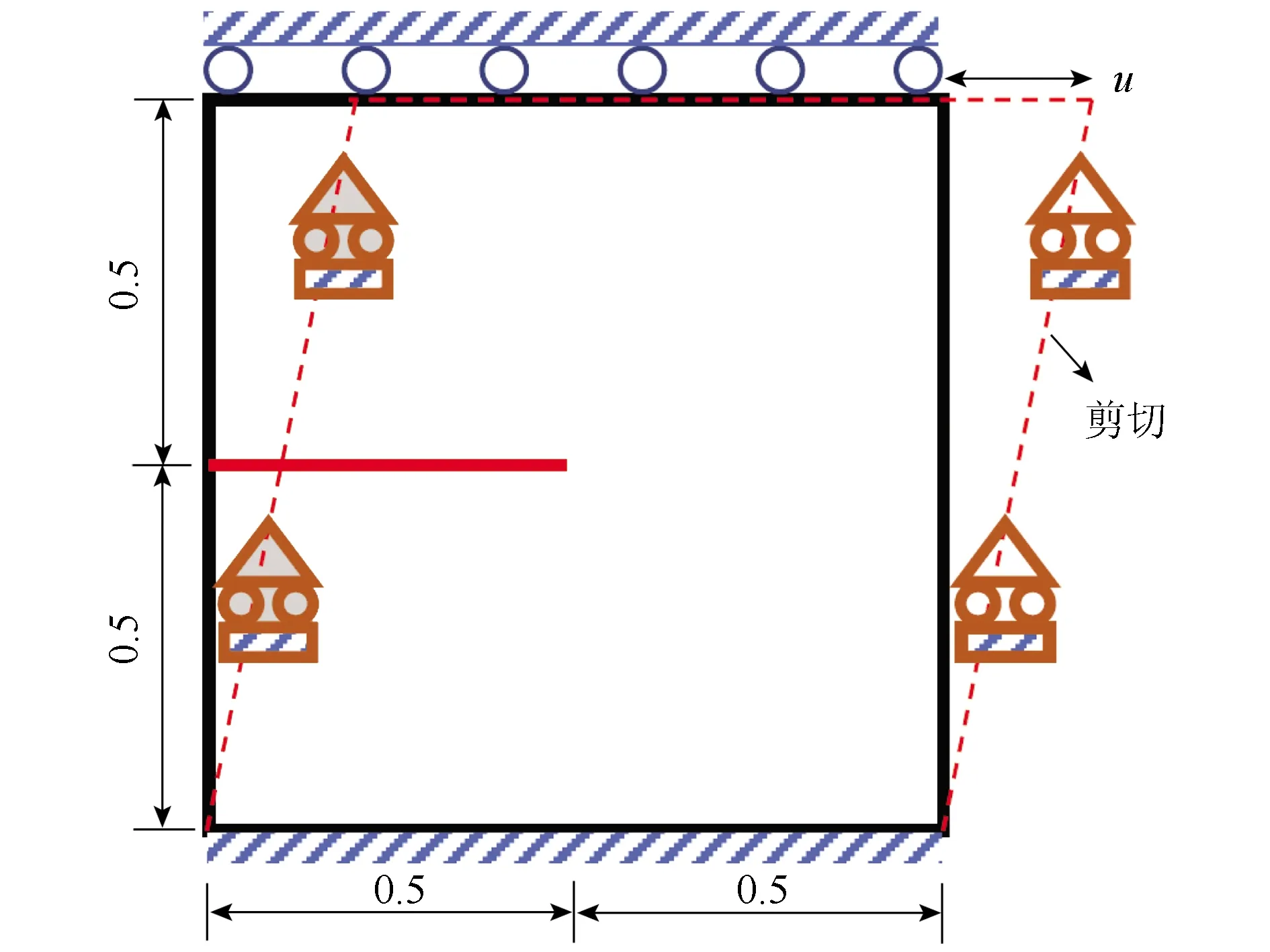
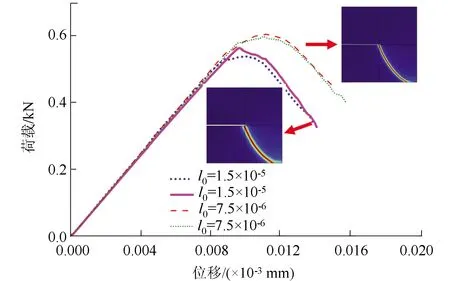
3 对称沉管隧道结构损伤区识别
3.1 襄阳东西轴线鱼梁洲隧道东汊沉管隧道简介
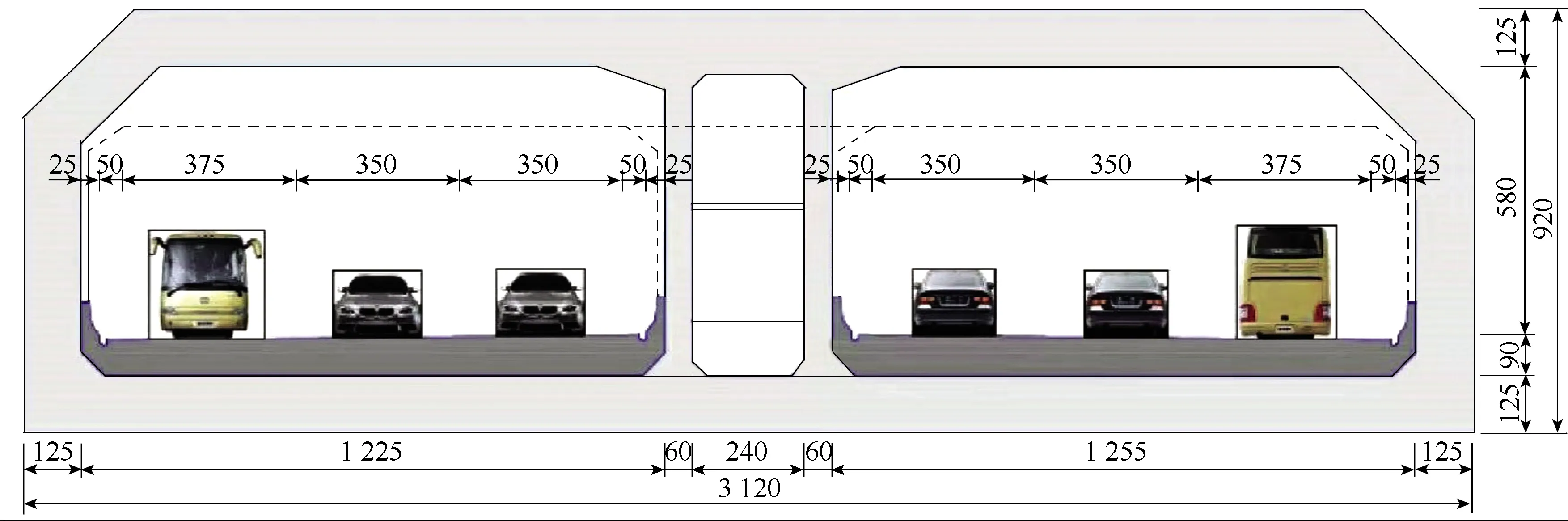
3.2 模拟过程
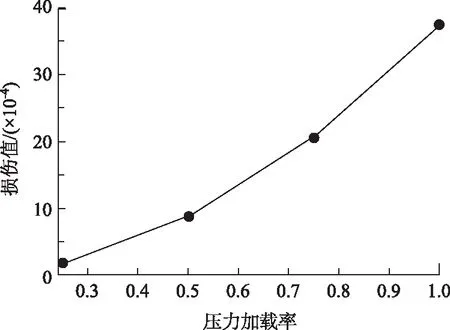
3.3 施工期结构损伤
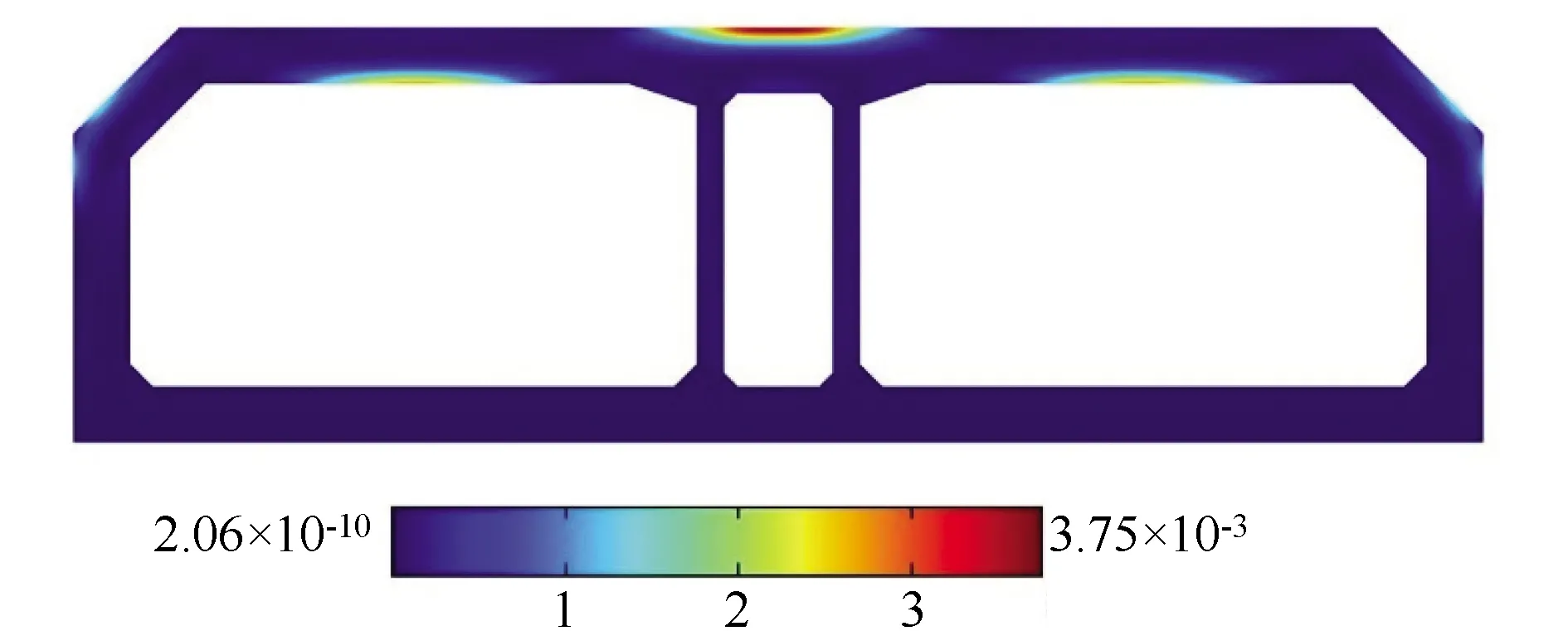
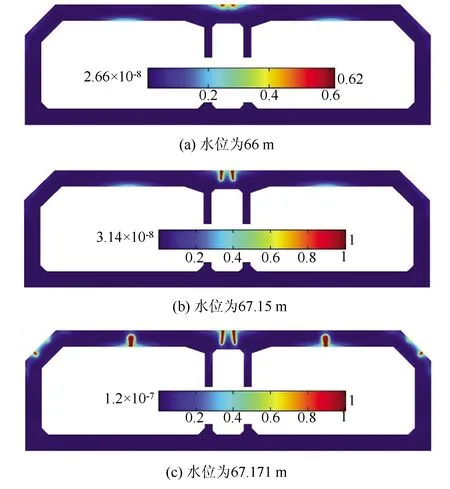
3.4 水位影响

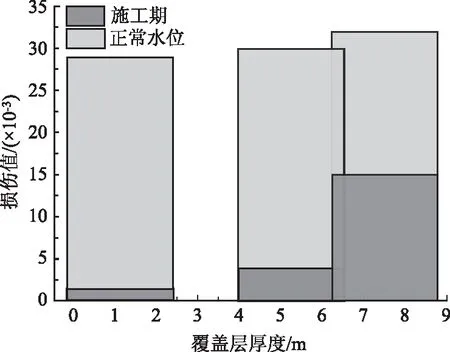
3.5 覆盖土影响
3.6 能量释放率敏感性分析


4 结论
