基于CART决策树的河北省低能见度分类研究

尤琦 曲晓黎,2 赵增保 王洁 张娣 杨琳晗

(1.河北省气象服务中心，河北 石家庄 050021； 2.河北省气象与生态环境重点实验室，河北 石家庄 050021)

引言

大气能见度也称气象视程，是表征大气透明度的重要物理量[1]。20世纪90年代以来，随着工业化和城市化的不断推进，我国近地面大气通透度和水平能见度持续下降[2-6]。人民生活、城市建设和交通运输等各方面的正常运行极大程度地受到低能见度天气现象的影响，亦成为诱发交通事故的主要气象因素。为保障交通安全提升高速公路通行效率，低能见度天气的精准预报需求日益增大。

国内外学者已对大气能见度预报开展了诸多研究。早期预报能见度的方法主要采用天气环流型分析、多元回归和模糊识别等方法[7-10]，通过对低能见度天气现象的形成条件进行诊断分析，并结合实况外推方法和主观经验做预报。然而，经验性和线性系统的预报方法并不适用于非线性强、数据来源不可靠性大的大气系统[11]，与此同时，数值模式不断深入发展，依托历史数据利用模式输出的要素进行预报模型构建[12-13]的方法也对能见度预报起到了一定的推动作用，但数据要求高、计算繁琐、参数不易设置，预报效果及业务化程度也不够理想。

与传统的统计分析和数值模式方法相比，机器学习对于提取数量庞大的气象数据、自动化调整参数等方面有更突出的表现，全球越来越多的学者将人工智能应用于气象业务研究领域。而机器学习作为其中一个重要分支，由于其模块化计算、易于调用、计算效率高等优点得到了广泛的应用，机器学习对要素的客观预报能够有效量化由于初始误差和模式误差所引起的不确定性，为提高预报预警服务能力提供技术支撑，例如神经网络[14-17]、支持向量机[18]和决策树[11,19-21]等经典机器学习算法。其中，决策树算法由于具有抽取规则简单、对数据缺测值不敏感、模型易于构建、速度快等特点，广泛应用于医学、农业、电力和气象等诸多领域。

本文拟通过统计分析河北省低能见度天气现象的发生规律，使用分类回归决策树算法(classification and regression tree ，CART)，分区域基于不同气象要素建立低能见度预测模型，对有关部门提高灾害的预警能力、灾害预测的准确性并实施有效的对策来趋利避害，具有十分重要的意义。

1 资料与方法

1.1 资料来源

资料包括河北省气象信息中心提供的全省142个DZZ4型国家气象站(图1)逐小时观测数据。数据时段为2016—2019年，要素包括各站整点的气温(℃)、气压(hPa)、相对湿度(%)、2 min风速(m·s-1)、2 min风向、小时内最高气温(℃)、小时内最低气温(℃)、露点温度(℃)、最低地表温度(℃)、最低能见度(m)、过去24 h变温(℃)和过去3 h变压(hPa)等共12种气象要素，以及各站逐月雾日数观测结果。雾日定义标准为：当一天内观测记录中出现雾现象，即记为一个雾日。

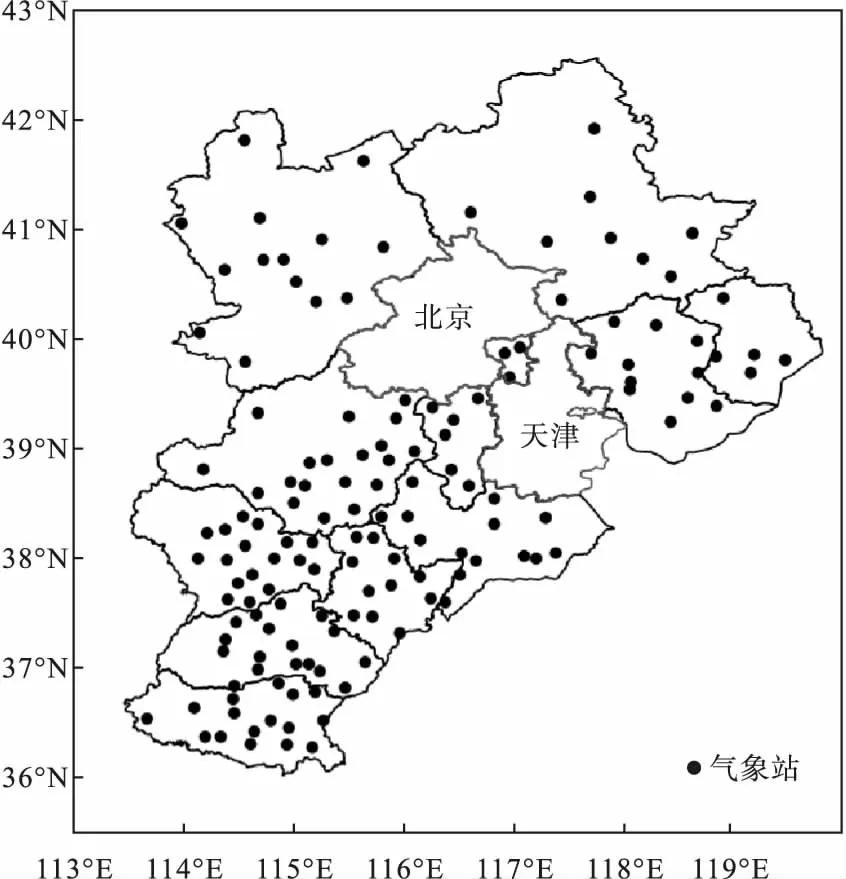
图1 研究区142个国家气象站分布

1.2 研究方法

1.2.1 (EOF)分解

经验正交函数(Empirical Orthogonal Function,EOF)分解就是将气候变量场分解为空间函数和时间函数两部分的乘积之和，将变量场的主要空间模态通过几个典型的特征向量最大限度表现出来的一种气候统计方法。

假设某包含m个空间点和n个时间点的变量场以矩阵X形式给出，将其展开为空间函数和时间函数的乘积，矩阵形式为X=VT，其中V表示空间函数矩阵，T表示时间系数矩阵，根据正交性质，二者应满足

(1)

λk为特征向量，第k个特征向量的方差贡献率为Rk

(2)

本文利用统计得到的2016—2019年河北省逐月雾日数资料，通过EOF方法，分析河北省逐月雾日数的时空分布特征。

1.2.2 分类回归树算法

CART决策树呈二叉树结构，由根节点、分支和叶节点三部分组成，常采用基尼指数(Gini)来衡量数据集的纯度，Gini指数越小样本类别的不确定性越小。算法从根节点开始，针对样本属性对每一个内部节点进行预测，新子节点也通过循环完成，若该节点中所有元素属于同一类别，则循环结束并标记该节点为叶子节点。

在分类中，对于一个给定的样本集合D，其中包含N个类别，则D所对应的基尼指数为

(3)

对于集合D，其包含N个样本，根据特征A的第i个值，将样本集合D分割成D1和D2，Gini系数为

(4)

在最优二分方案下选取最小值，作为样本D的方案

minA∈Attribite{mini∈A[GiniA,i(D)]}

(5)

在不加限制的情况下，一棵决策树可以生长到纯度最优，这样训练集拟合效果很好，测试集拟合效果差，把这种现象称为过拟合。下采样时多数类别样本数量相对于少数类别样本数量的比例为1时，即无雾日数与有雾日数相同时，模型严重过拟合；不设置任何参数时，模型同样过拟合。因此，通过下采样和网格搜索法剪枝处理来防止上述现象的发生。

将与能见度显著相关的气象要素作为特征A输入，并将能见度分为有无雾两个类别，即N=2，对总体样本D进行循环分类，直到某样本D中所有元素属于同一类别，决策树停止分类。

1.2.3 模型构建与检验

建立能见度预测模型的过程大致如下：首先根据输入显著相关气象要素，并对能见度ong-hot编码作为目标变量；其次采用下采样方法，从多数类别数据中随机抽取样本减少多数类别数据，使数据达到相对平衡；接着随机选取部分数据作为训练集，利用Scikit-learn模块中的CART算法建立模型，得到预测规则集；最后利用未输入模型的数据检验模型预报结果。

通过样本的采集，能够直接知道真实情况下，哪些数据真实值是第一类别和第二类别。同时，通过模型分类结果，也可得出两类数据，因此就会出现四类结果：

真实值是第一类别，模型认为是第二类别的数量(True Positive=TP)，即对应真实有雾且预报出有雾的1481个时次数据；真实值是第一类别，模型认为是第二类别的数量(False Negative=FN)：这就是统计学上的第二类错误(Type II Error)，即对应真实有雾但未预报出有雾的681个时次数据；真实值是第二类别，模型认为是第一类别的数量(False Positive=FP)：这就是统计学上的第一类错误(Type I Error)，即对应真实无雾但预报出有雾的867个时次数据；真实值是第二类别，模型认为是第二类别的数量(True Negative=TN)，即对应真实无雾且预报出无雾的137017个时次数据。

2 结果分析

2.1 河北省雾日时空分布特征

2.1.1 空间分布特征

华北地区大雾频发，已经引发社会的广泛关注[19，23-24]。图2显示：河北省除张家口、承德及秦皇岛三市外，40°N以南地区为雾日高发区域，多年平均雾日数最高可达50 d，其中邯郸、邢台及石家庄南部，保定东部、衡水北部、沧州西北部地区雾日数较高。

单位为d

为确定研究区域，将2016—2019年逐月雾日数做经验正交分解(图3)，得到前3个模态方差贡献分别为60.17%、24.15%和4.97%。第一模态空间分布特征(图3a)与多年平均雾日分布图呈现较为一致的分布型，河北省内40°N以南地区为负值，对应第一时间系数先正后负的下降趋势(图3d)可以得出河北南部地区逐月雾日数呈现先负距平后正距平的变化特征，即在2017年底前雾日数相对2016—2019年平均雾日数偏少，2018年及以后相对偏多；第二模态(图3b)也存在一定的南北相异型分布特征，除此之外保定东北部、石家庄中东部以及邯郸等地出现了负值中心，结合第二时间系数(图3e)由负转正的变化趋势来看，上述地区在2016年和2017年雾日高发；第三模态(图3c)除秦皇岛市几乎呈现全区一致型分布特征。因此，结合第一、第二空间模态分布特征，本文选取石家庄站作为雾高发地区代表站进行深入研究。

图3 2016—2019年河北省逐月雾日数的第一(a)、第二(b)和第三(c)空间模态与第一(d)、第二(e)和第三(f)时间系数

2.1.2 时间分布特征

经统计石家庄市每年10月至次年1月为雾高发时段，每日逐时雾发生频次较高时段集中在夜间21时至次日8时(图略)。因此，本文针对该统计结果将数据集分为冬夜、冬日、夏夜、夏日四个时段分别进行建模和检验。其中，冬季高发时段(简称冬季)定义为每年10月至次年1月，夏季高发时段(简称夏季)定义为2—9月；白天定义为每日09—20时，夜间定义为每日21时至次日08时。

2.2 能见度主要影响因子分析

在利用CART算法构建决策树前，选取石家庄地区的最小能见度数据作为目标变量，通过对能见度的影响因子进行分析，分别确定对最小能见度的影响因子，确定输入的气象要素。参照《高速公路能见度监测及浓雾的预警预报》(QX/T 76—2007)运营管理规定，将影响高速公路运营的能见度划分为2个级别，以能见度750 m为阈值，小于750 m记为有雾，标记为数值1，大于750 m记为无雾，标记为数值0。

已有不少学者研究发现能见度与湿度、风速等因子显著相关[25-26]，石家庄地区最小能见度数值和同期各气象因子的相关性表明(表1)，过去3 h变压、相对湿度两个因子与能见度数值呈负相关，其余要素均与能见度呈正相关。其中，2 min风速等9种要素与最小能见度的相关系数值通过了α=0.01的显著性检验，可作为输入变量。由于逐小时的最高最低气温与整点温度数值差别不大，因此输入变量以整点气温为准，同理地表温度作为输入变量。

表1 各气象因子与能见度相关系数

2.3 模型构建及效果评估

调参过程中先对参数画出学习曲线，预估一个大概范围，然后用网格搜索法确定最终值，以减少搜索时间。决策树算法核心属性是max_depth(最大深度)和criterion算法的选择，这两个参数直接影响决策树的精确度。经调参，模型最佳参数组合为criterion=gini，max_depth=6，min_samples_leaf=2，下采样时多数类别数据与少数类别数据比例为25。

将调试评分最高的参数带入决策树算法中进行训练，训练集使用2016—2018年石家庄观测站逐时资料，其中70%训练，30%用以自测，模型自测评分达到97.4%(图4)。

图4 模型参数max_depth评分结果

值得注意的是，模型自测混淆矩阵中，由于无雾时次的预报占相当大的比重，而本研究关注的有雾时次占比相对较少，因此不同于前人研究中的模型检验，本研究参考THORNES等[22]的天气预报评定方法，利用混淆矩阵，对比分析模型预测的准确率、漏报率和空报率。

由于决策树最下层共62个叶子节点，不便于展示全部分支，节选部分决策树如图5所示。以最上层节点为例，“air≤5.5，value=[574,2417]，gini=0.31，class=1”表示以气温5.5 ℃为分界点，小于该阈值为类别0，大于该阈值为类别1，两类数据的样本量分别为574和2417，基尼指数为0.31。

图5 能见度分类决策树部分图

经统计，该模型的预报有雾时次的准确率为1481/(1481+681+867)=48.9%；漏报率为681/(681+1481)=31.5%；误报率为867/(867+1481)=36.9%(图6)。若不剪枝和下采样，使用原数据建模后TS评分仅为16%，虽然每次抽样后训练集会有所变化导致模型在4至5层时略有不同，但整体TS评分均保持在47%—51%左右。较好地将少数类别样本与多数类别样本区分开，并且对于有雾时次的预报准确率优于神经网络的预报结果。

图6 混淆矩阵检验结果

按照上述统计方法，针对石家庄地区的低能见度情况进行分类预报检验表明(表2)，冬季低能见度天气预报准确率显著高于夏季，夏季漏报情况也显著多于冬季，但夏季误报率却低于冬季。说明该模型对于冬季的预报效果较好，但其较高的准确率会伴随着较高的误报率；夏季的预报效果略低，其漏报率较高，但误报率较低。日夜差别在夏季并不明显，三个指数差别不大，冬季夜晚的准确率与误报率明显优于白天，漏报率略高。这可能是由于冬季昼夜变温相对夏季不明显造成的结果，并且本文的资料中并未引入污染物数据，因此模型训练中无法考虑霾导致的低能见度天气现象，冬季华北地区的雾霾现象也会造成误报漏报的情况，具体原因值得深入研究。

表2 不同时段预测检验结果

为进一步检验模型，图7给出石家庄2019年12月7—10日的3次大雾过程拟合情况。经统计，12月7—10日共96个时次，漏报率为0，真实有雾且预报有雾的时次数为36次，误报数为20次，真实无雾且预报为无雾的时次为40次。

由图7可以看出，该模型对3次低能见度天气的拟合结果较为理想，无漏报。对于8日夜间和10日凌晨能见度高于750 m小于1000 m的情况误报为有雾，考虑到低于1000 m的轻雾对交通也存在一定的影响，可以认为模型的模拟效果较好。

图中蓝色实线表示各时次能见度数值随时间变化的实况，红色点表示模型预报有雾的结果，蓝色点表示模型预报无雾的结果

3 结论与讨论

(1)河北省除张家口、承德及秦皇岛三市外40°N以南地区为雾日高发区域，石家庄市东南部地区多年平均雾日数峰值可达50 d。逐月雾日数EOF第一模态方差贡献占比60.17%，空间分布特征与多年平均雾日数分布较为一致，且时间系数显示雾日数呈现逐渐增多的变化特征。

(2)基于CART决策树方法建立低能见度预测模型，当参数调整为criterion=gini，max_depth=6，min_samples_leaf=2，下采样时多数类别数据与少数类别数据比例为25时该模型检验结果最优，其对石家庄地区逐时低能见度天气的预报结果准确率达到48.9%。

(3)该模型对于冬季的预报效果较好，但其较高的准确率会伴随着较高误报率；夏季的预报效果略低，其漏报率较高，但误报率较低；日夜差别在夏季并不明显，三个指数差别不大，冬季夜晚的准确率与误报率明显优于白天，漏报率略高。

(4)大雾天气过程检验结果显示，石家庄站2019年12月7—10日的3次大雾过程拟合结果较好，有雾时次无一漏报，考虑到低于1000 m的轻雾对交通也存在一定的影响，可以认为模型拟合结果较为出色。

(5)过去对能见度的研究大多集中在1—10 km范围内，并且传统的统计学模型无法针对突变性很强的能见度数值进行预测分析。本文主要针对1 km以下的能见度进行分类预测，且模型预测效果较好。但该模型均基于实况数据进行建模、检验，后续需要将实况和预报数据结合输入并调参，以期对于能见度的分类预报能有所提升。