零点的隐与现
——兼论2022年全国乙卷第16与21题
2022-08-02黄秋帆
黄秋帆
(北京师范大学教育学部)
1 零点的定义与隐零点概念澄清
对于函数y=f(x),使f(x0)=0的实数x=x0叫作函数y=f(x)的零点,即函数y=f(x)的零点就是方程f(x0)=0的实数根,也就是函数y=f(x)的图像与x轴交点的横坐标.
从零点的定义不难看出,初学者可能会将零点与坐标混淆.而零点的问题一般转换为求解普通方程,或是直接通过画图转换为函数图像交点问题.函数零点问题中最让广大学生头疼的还是复杂零点代换与隐零点问题,历年的模拟考试与高考中隐零点问题都是“拦路虎”.
中学数学中并没有给出隐零点的规范定义,从自然定义的角度来说,隐零点是零点的一种,只是出于种种原因隐而不现.如何找到隐零点,然后通过研究其存在范围与满足的等量关系实现消元成为重要的问题.
在高中阶段,研究隐零点存在性的方法为零点存在定理,证明隐零点唯一性的方法为单调性法.使用零点存在定理时,有两种方案分别是极限取值法与“找点法”,极限取值法本质上也是一种“找点”,只不过无穷并不是一个值,需要用极限来表述.需要指出的是,对隐零点的普遍误解有以下三点.
1)隐零点在大部分情况下是固定的一点,它可以随参数而动,但本质上并不是自变量,所以它并没有所谓的“定义域”或“取值范围”,而大多数人指称的隐零点“取值范围”实际上是在已知存在性的前提下,因为人力无法解出超越方程,对其范围的一种妥协,故称其为“存在范围”更为合理.
2)我们在对隐零点满足的关系进行换元时,换元后实际上已经是另一个函数了,只有x=x0时才能实现完美代换,即两个函数交于x=x0,其余点都存在与原函数相比的误差,因此对隐零点的范围估计决定了误差的大小,这一点笔者会在后面的例题中通过画图进行阐释.
3)我们是否一定需要知道隐零点的具体范围?实际上并不一定.这一点在2022年全国乙卷第16题中可以得到体现.
2 例题的分类与讲解




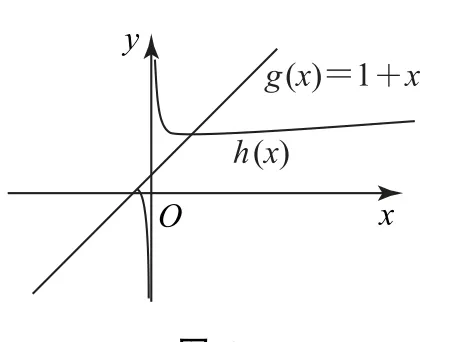
图1





此题涉及原函数与导函数、二阶导数的关系,由于指对混合函数的特殊性,无法得到具体的零点、极值点和拐点的位置,但是可以通过不断地用零点存在定理和单调性进行拆分,得出三个函数的隐零点,从而推出f(x)单调性,最终再用一次零点存在定理得到答案.与之前几道题都不同的是,隐零点在这道题中并不需要进行等价代换.此题在思维上并不复杂,但是需要学生有扎实的基本功以进行运算.
