基于自适应事件触发的复杂网络的非脆性安全同步控制

李杨,潘荣清

(1.江苏开放大学教育学院,江苏 南京 210013;2.南京财经大学应用数学学院,江苏 南京 210023)

1 引言

复杂网络是由大量节点构成的一类大规模网络系统,其中不同的节点代表具有某种特定动力学特性的个体,而边缘则代表了这些个体之间的关系.最近几十年,由于网络化信息技术的快速发展,复杂网络在物理,医学,生物网络和食品网络等领域得到了广泛的应用[1-4].因此,研究其动态行为以及相关问题是极具理论和实际价值的.

在诸多问题里,同步问题作为复杂网络研究中十分重要的一个问题,其普遍存在于各个系统之中,与系统能否正常运行有着紧密的联系.因此,同步一直是各领域学者关注的热点[5-8].目前,同步控制的定义很多,如完全同步[9-11],牵制同步[12-13],有限时同步[14-16].本文考虑的同步是驱动-响应系统的同步,其基本原理是驱动系统通过向响应系统传递系统信号来使响应系统与之达到同步[17].随着研究的深入,学者们将驱动-响应系统的同步问题与其他控制问题相结合,得到了很多有意义的结果.例如,文献[18]研究了耦合复变混沌系统驱动响应系统的复数投影同步.文献[19]研究了具有耦合时变时滞的复杂网络驱动响应系统的有限时间混合外同步问题.然而,对于具有随机动态行为以及时变时滞的非线性复杂网络网络系统的驱动响应同步控制还没有得到充分的研究.因此,利用随机性分析技术研究复杂网络系统的同步控制问题是第一个动机.

在科学技术高度发展的今天,复杂网络系统的规模越来越大,网络通讯信道中的数据传输也越来越频繁,然而,传输信道的带宽是有限的,这就可能会导致网络负载以及数据传输的拥塞,从而降低系统的运行效率,使系统的稳定受到严重的干扰.因此,设计出能在保证系统性能的同时有效降低网络负荷的机制变得很有必要.当前人们普遍引用事件触发控制方法来解决负荷问题,其基本思想是预设出触发约束条件,并以此来判断当前采样信号是否需要发送到下一个控制终端,从而减少不必要的信号传递.

在现有的文献中,事件触发机制的应用已经十分普遍[20-22].例如,在文献[20]中,基于事件触发机制,具有固定时滞的复杂网络状态估计问题被提出并解决.在文献[21]中,通过引入分布式事件触发传输策略,考虑时变内部耦合,一类复杂动态网络系统的指数同步问题得到了讨论.然而,事件触发机制的触发阈值几乎都被设计成常数,这意味着其无法随系统状态变化而动态调整数值,故节约资源的效率是有限的.为了解决这个问题,包含不定阈值的自适应事件触发机制被设计了出来[23].随后,又有很多学者进行了研究并得到了许多有意义的成果[24-27].

另外,考虑到数据交互层无线通道的开放性原则,以及感知层传感器节点部署的随机性,信号在网络中传输极有可能受到来自外部的威胁.在威胁网络安全的各个因素之中,网络攻击是最常见也是最具威胁的.网络攻击会使系统的信息被盗取,破坏或篡改,也会使系统产生严重的时滞以及大量的丢包,从而导致系统内部元件无法正常运行甚至会发出错误的信号.因此,系统可能会变得不再稳定,最终瘫痪.近年来,随着研究的深入,以及相关论文的发表,网络攻击在控制领域成为了重点问题[28-30].然而,据作者所知,对于复杂网络系统的安全同步控制几乎没有相关的文献.因此,更一般的复杂网络在自适应事件触发和网络攻击下的安全同步控制问题仍然具有挑战性,有待进一步解决,这也是本研究的另一个动机.

目前,虽然已经有一些关于复杂网络同步控制问题的研究,但是这些成果基本都是基于传统的控制器取得的,鲜有基于自适应事件触发的非脆控制器问题.本文基于上述讨论,考虑欺骗攻击以及随机动态行为的影响,并结合复杂网络系统的特征,引入分散式自适应事件触发传输机制,建立具有时滞的复杂网络驱动响应系统的同步误差模型,使复杂网络系统达到所需的同步状态.

本文以下,Rn表示n维欧氏空间.I表示具有适当维数的单位矩阵.‖·‖表示欧几里德向量范数.diag{·}代表分块对角矩阵,而diagn{Xi}则表示diag{X1,X2,···,Xn}.col{X}表示将X按列矩阵的形式书写,coln{Xi}表示符号X|A=B意思是将矩阵X中的A用B替换掉.E{X}表示随机变量X的期望值.(t)表示函数V(t)的导数.⊗表示矩阵的Kronecker积.

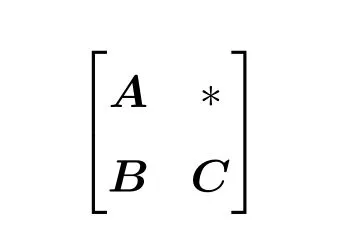
表示一个对称矩阵,其中*表示被隐藏的与矩阵B以及对称矩阵A和C对称的项.

2 模型概述

首先给出由N个节点组成的复杂网络的驱动系统模型:

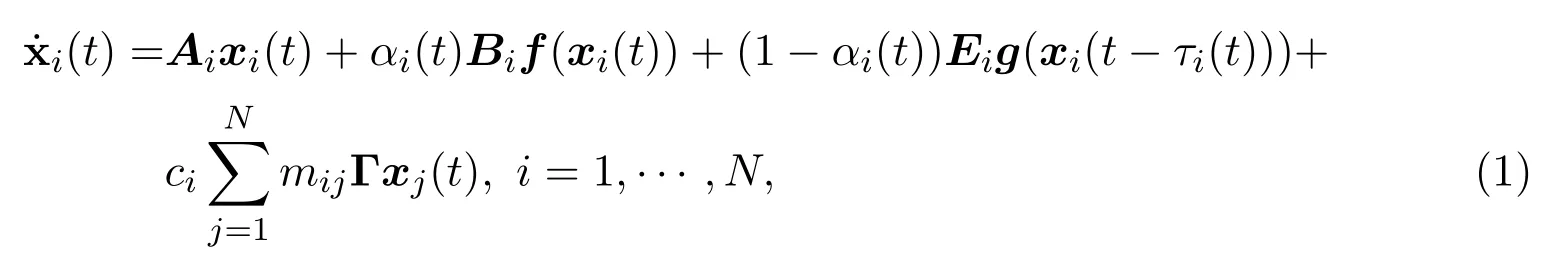
其中xi(t)是第i个节点的状态变量,Ai,Bi,Ei为已知的系数矩阵.f(·),g(·)为确定网络节点动态行为的连续可微函数,αi(t)∈{0,1}是服从伯努利分布的随机变量,且其期望设为

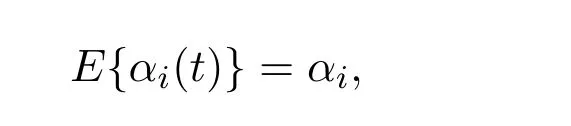
方差设为

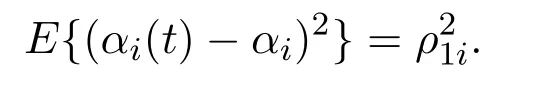
τi(t)∈(0,τi]是状态的时变有界时滞.ci表示耦合强度.M=[mij]N×N是网络的外部耦合矩阵,mij≥0(i/=j)且不全为0.一般地,假设M是对称矩阵且满足

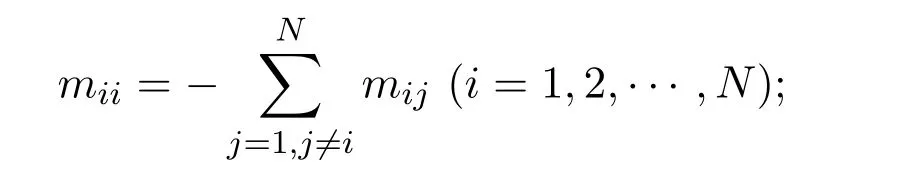
Γ是描述耦合节点状态变量之间的连接关系的内部耦合矩阵.

注2.1考虑到在不确定的网络环境下,网络节点的动态行为可以随机变化,引入随机变量αi(t)来描述这种动态行为.在系统(1)中,可以很容易看出非线性函数f(·)和g(·)是根据αi(t)的变化来进行随机切换的.

考虑对应的响应系统模型如下:

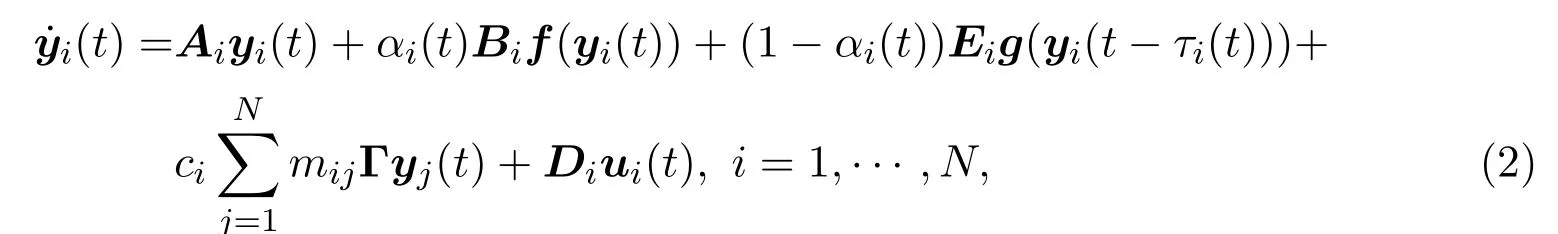
其中Di为已知的系数矩阵,ui(t)是系统的控制输入.

定义系统的状态同步误差εi(t)=yi(t)-xi(t),可以得到如下的驱动响应同步误差系统模型:

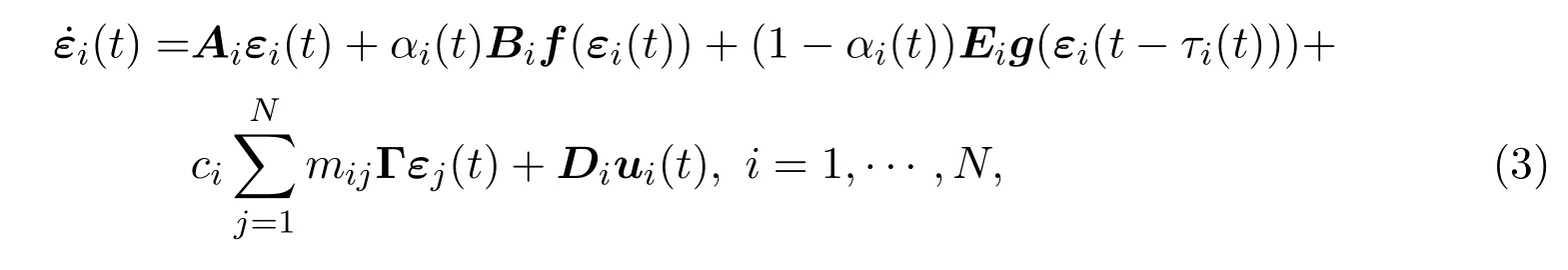
其中

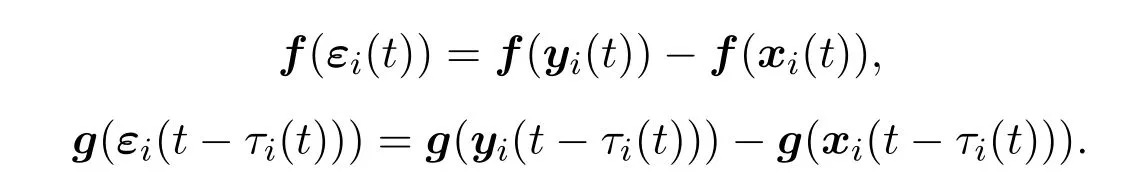
注2.2当(3)式=0时,意味着输出系统和响应系统的信号达到一致,即整个驱动响应系统达到同步状态.

目前,信息技术正在飞速发展,复杂网络系统中传输信息越来越庞大,然而网络带宽是有限的,因此在保证系统性能的情况下节约有限的网络资源,本文在每个节点的传感器和控制器之间引入了一个自适应事件触发机制.

为了便于描述,对第i个网络节点在自适应事件触发时的传输数据和传输时刻做以下假设

假设2.1假设系统的传输时间为(k=0,1,2,···),其中h是采样周期,(k=0,1,2,···)是非负整数.此外,设传输的初始时刻为t0h=0.

自适应事件触发规则的数学模型如下:

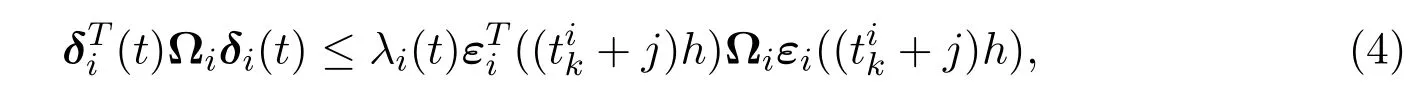
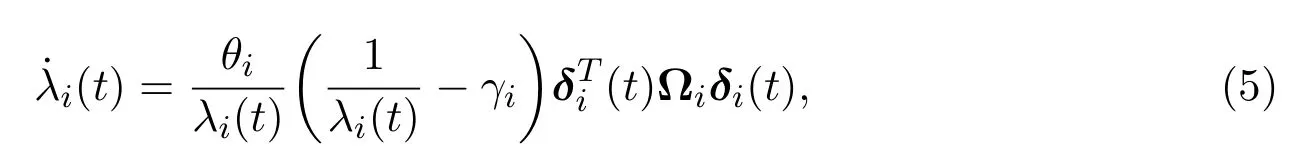
其中0＜λi(t)＜1,θi＞0,γi＞0.

根据不等式(4),假设上一个传输时刻为,则下一个传输时刻满足如下条件:

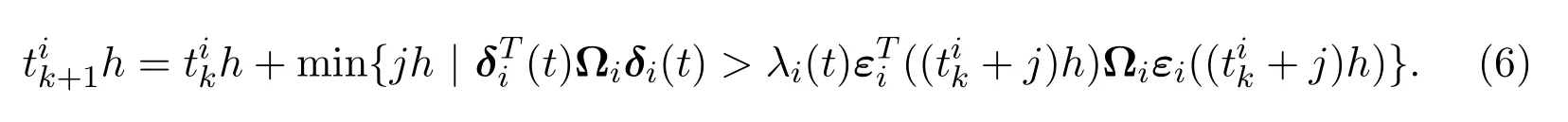
考虑到信号在传输的时候会不可避免地产生传输时滞,本文用符号来描述这个时滞,并且假设由此,可以传输的信号到达控制器的时间t满足

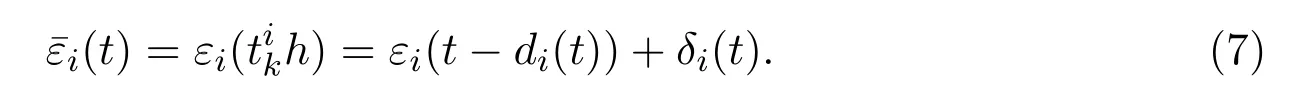
注2.3相较于传统的事件触发机制,本文所采用的自适应事件触发机制的阈值参数并不是固定的常数.此外,由(5)式,易知λi(t)是根据误差状态δi(t)变化而改变的变量,并且其导数(t)→0当且仅当δi(t)→0,这意味着只有当系统不存在使其不稳定的扰动的时候,阈值参数才会收敛到一个常数.

注2.4Zeno行为是指事件触发机制在有限时间内无限触发的情形,而根据自适应事件触发条件(4),可以知道本文中的数据采样是在离散时间(k=0,1,2,···)进行的,这意味着最小事件触发间隔是采样周期h,故不存在Zeno行为.

在控制器运行过程中,由于网络波动等其他不确定因素的影响,控制器很容易产生小的增益变化,为了处理这一问题,本文考虑的是含有不确定项的非脆控制器,其数学模型为ui(t)=(Ki+ΔKi)εi(t),其中ΔKi是在控制器执行过程中产生的不确定增益.由于引入自适应事件触发机制,实际的控制输入可以写成如下形式:

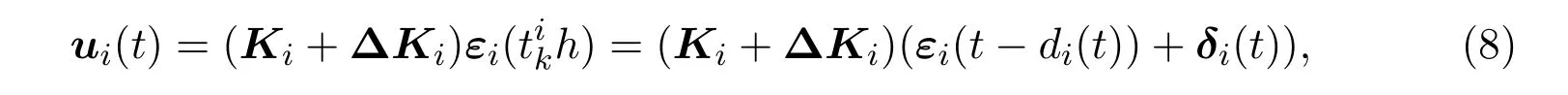
其中Ki是待定的反馈增益矩阵,ΔKi是未知但范数有界的矩阵.设ΔKi=SiF(t)Li,其中Si和Li是已知的常数矩阵,F(t)是时变矩阵函数,且满足FT(t)F(t)≤I.

考虑网络通信的开放性,系统所传输的控制器信号难免受到恶意的破坏,盗窃或泄漏,这可能会导致控制器无法正常工作或发出错误的控制指令,进而使系统变得不稳定,甚至崩溃.在本文中,假设控制器受到的攻击形式是随机的欺骗攻击,并且其攻击信号用与控制输入ui(t)有关的非线性函数h(·)来表示.

在网络攻击环境中,(8)式可以被改写成如下形式:

其中βi(t)∈{0,1}是满足伯努利分布的随机变量.为了讨论的便捷,假设

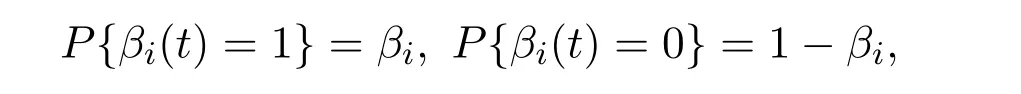
则攻击概率的期望为E{βi(t)}=βi,方差为

注2.5根据(9)式,可以知道如果αi(t)=0,则¯ui(t)=ui(t),这意味着当前控制器没有受到网络攻击.而如果αi(t)=1,则有¯ui(t)=ui(t)+h(ui(t)),这意味着控制器携带了恶意的攻击信号.

结合(3)式以及(9)式,将误差系统模型改写成如下形式:

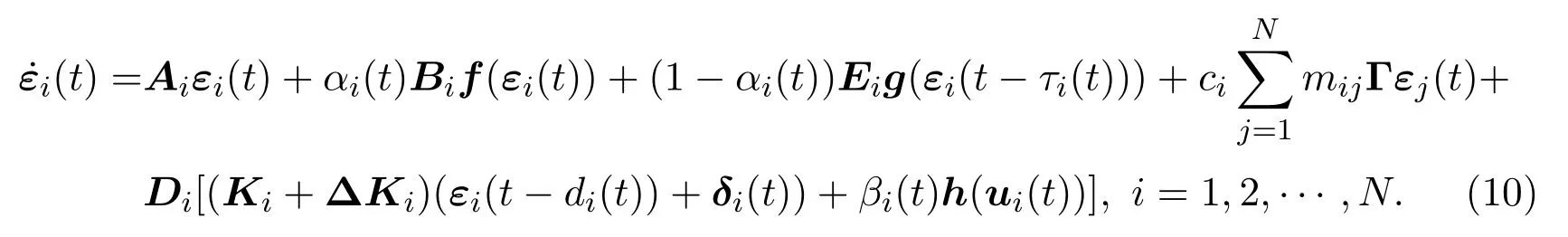
通过使用矩阵的Kronecker积,可以写成紧凑的形式:

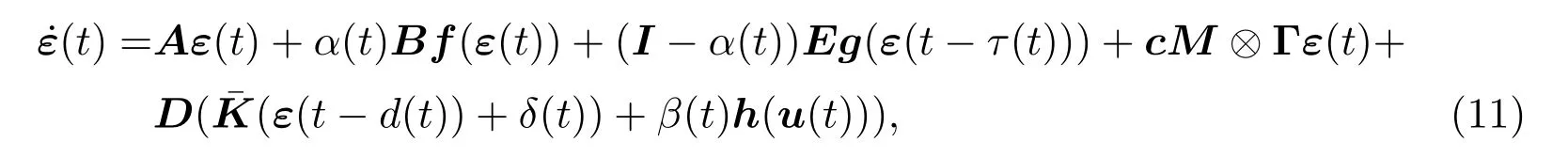
其中

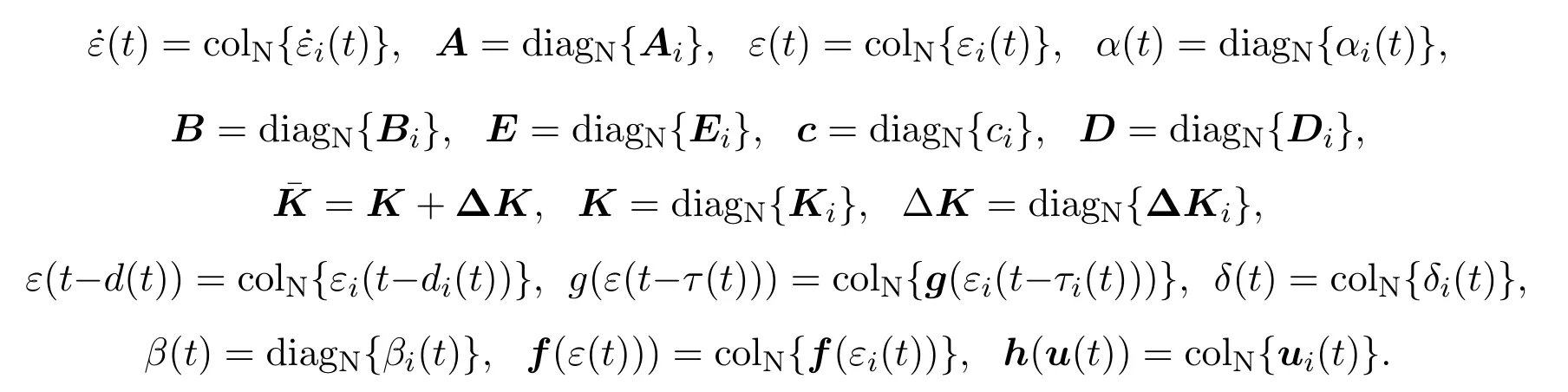
为了得到本文所需的结果,给出以下的假设,引理:

假设2.2对每个节点i,攻击信号函数h(·)和向量值函数f(·)以及g(·)都是连续非线性函数且满足如下的Lipschitz条件:

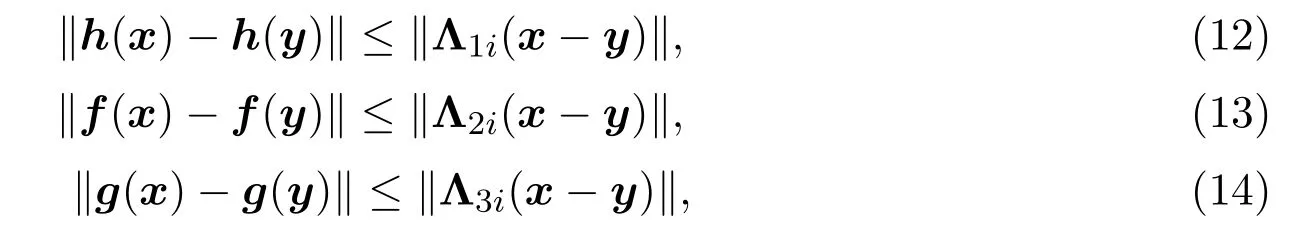
其中Λ1i,Λ2i和Λ3i是常数矩阵且分别表示h(·),f(·)和g(·)的上界.

引理2.1[9]给定常数d,若函数d(t)满足d(t)∈(0,d],则对于˙ε(t):(0,d]→Rn,存在矩阵Q＞0,使得如下矩阵不等式成立:

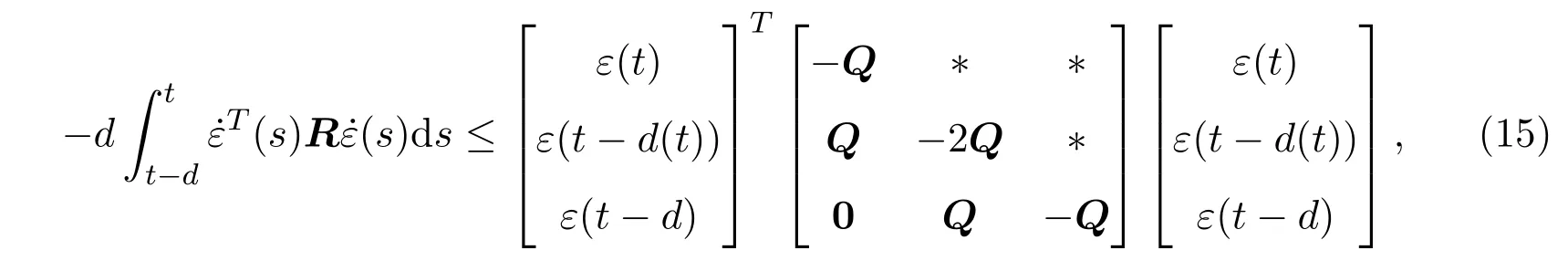
引理2.2[10]假设T1和T2具有合适维数的实矩阵,F(t)满足FT(t)F(t)≤I,则对于任何标量ι＞0,如下不等式成立:

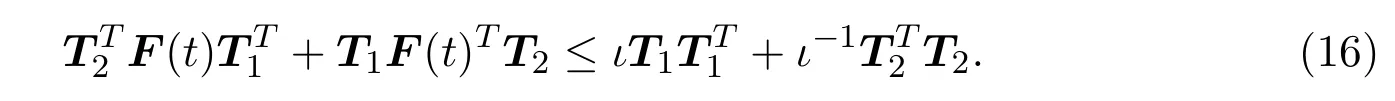
引理2.3[21](schur补引理)对于给定矩阵其中如下条件是等价的:

(1)S＜0;

3 主要结果

在本章节中,将会应用Lyapunov泛函方法来给出同步误差系统(11)渐近稳定的充分条件.另外,通过借助matlab软件中的LMI工具,可以得到每个节点的控制器增益Ki以及自适应事件触发的参数矩阵Ωi.

3.1 稳定性分析

定理3.1对于一些给定的正标量参数

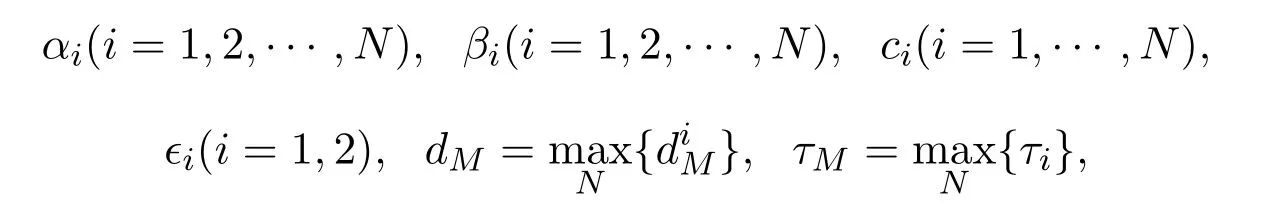
以及矩阵Γ＞0,A＞0,B＞0,E＞0,Λi(i=1,2,3),θ,γ,Ω和,误差系统(11)是渐近稳定的,若存在对称矩阵P=diagN{Pi}＞0,Ri(i=1,2)＞0,Qi(i=1,2)＞0,使得如下不等式成立:

其中Π11=

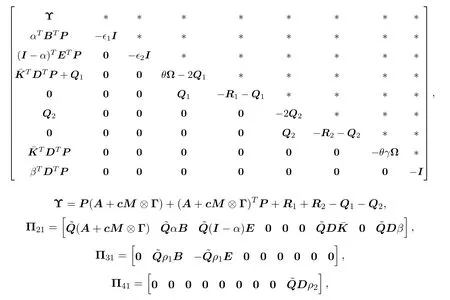
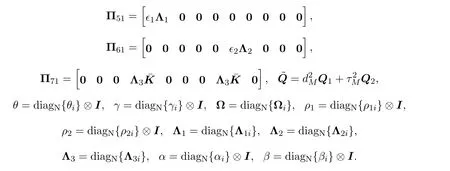
证明选取如下形式的Lyapunov泛函:

其中

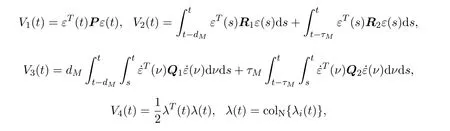
P＞0,Ri＞0(i=1,2)和Qi＞0(i=1,2)是待定的对称矩阵.

对V(t)关于t进行求导并取期望,可得

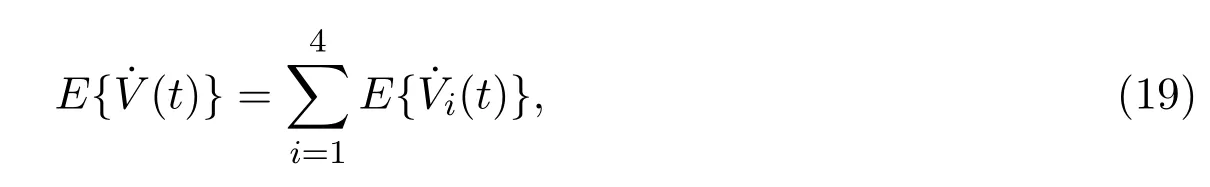
其中

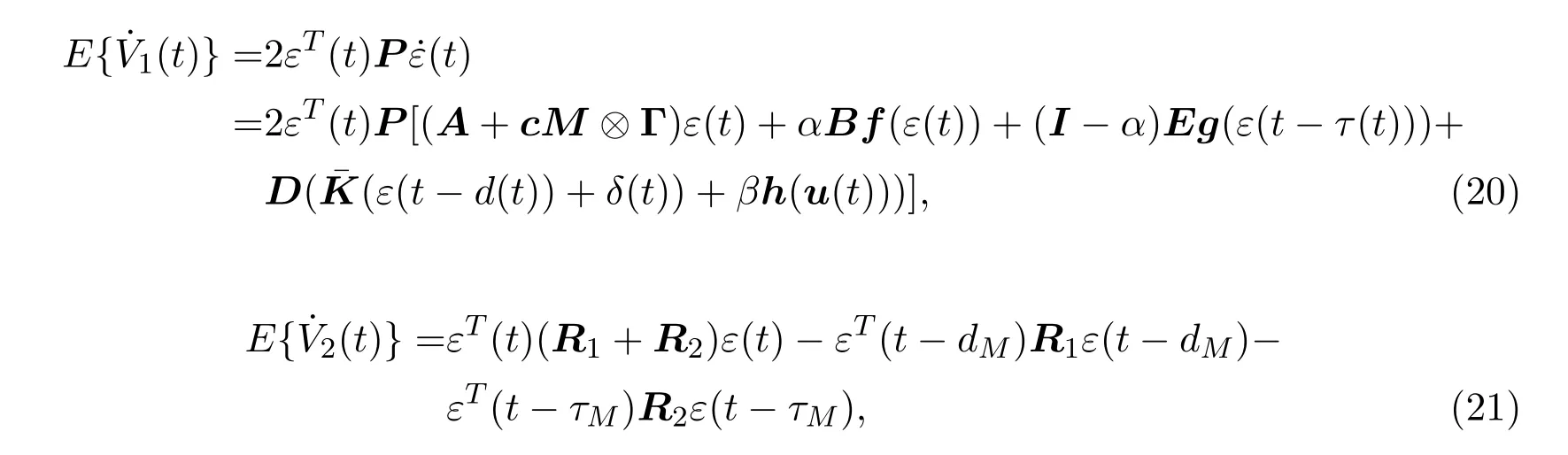
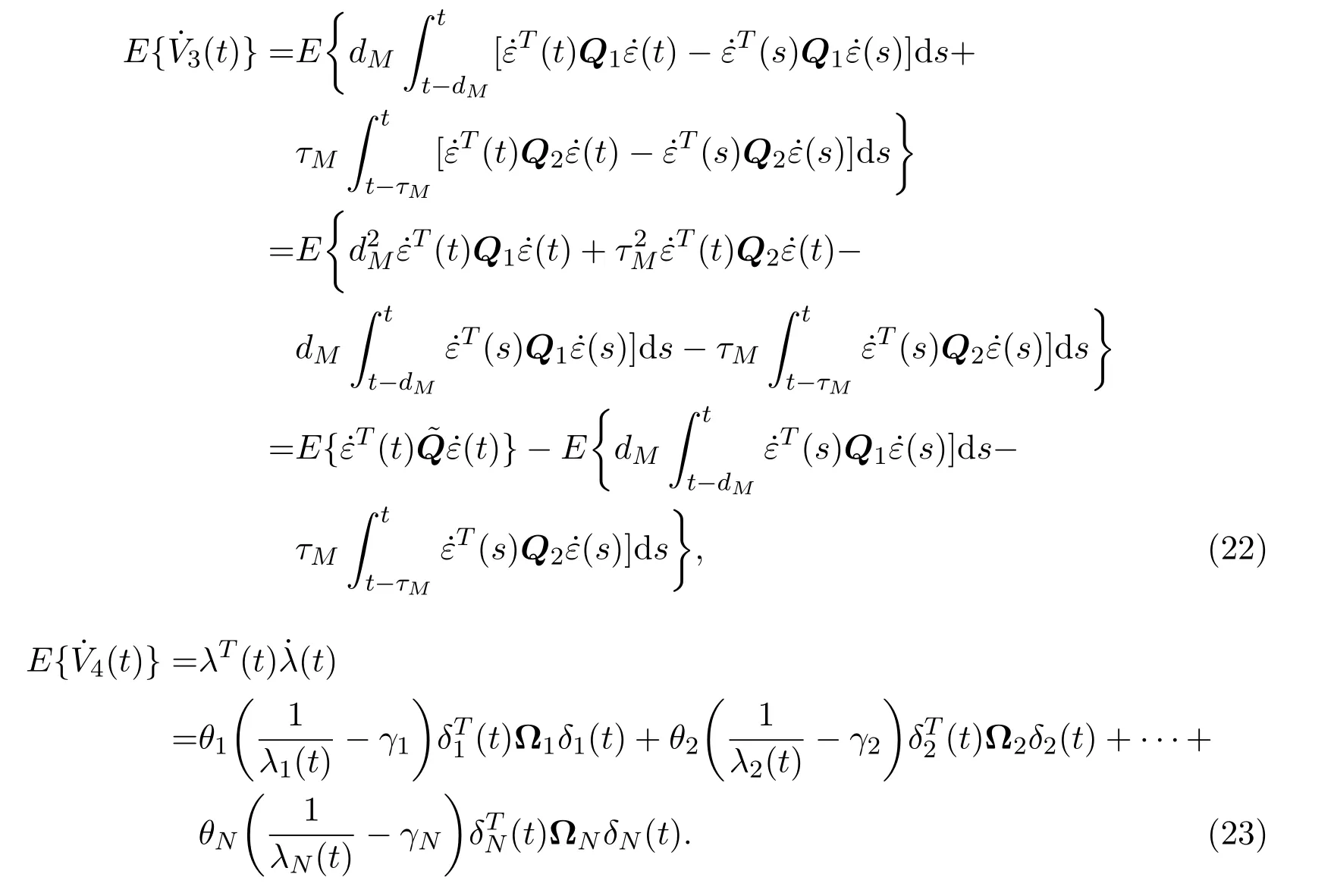
结合(4)式和(23)式,可以知道

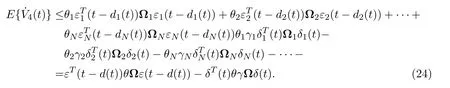
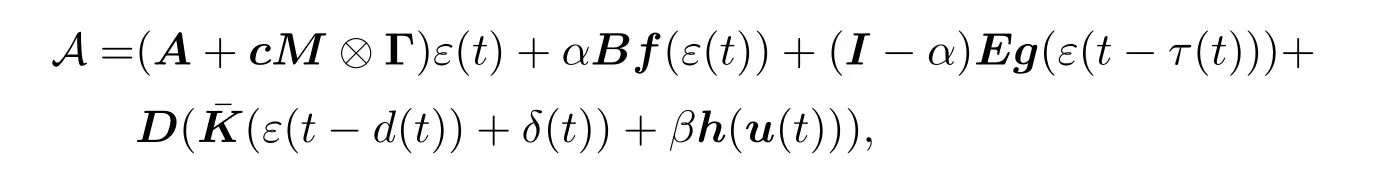
B=Bf(ε(t))-Eg(ε(t-τ(t)))和C=h(u(t)).由此,可以得到如下等式:

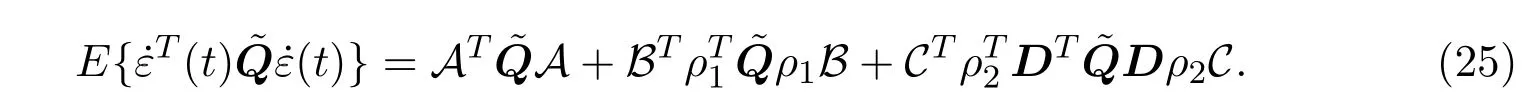
基于假设2.2,可以得到如下两个不等式:

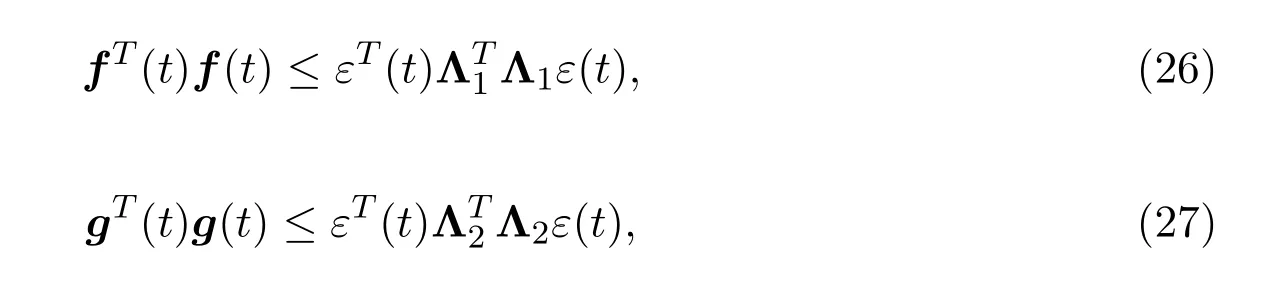
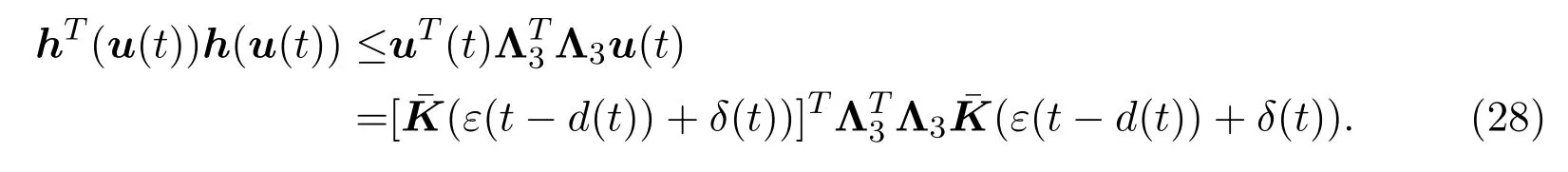
结合(20)式-(28)式和引理2.1,可得如下不等式:

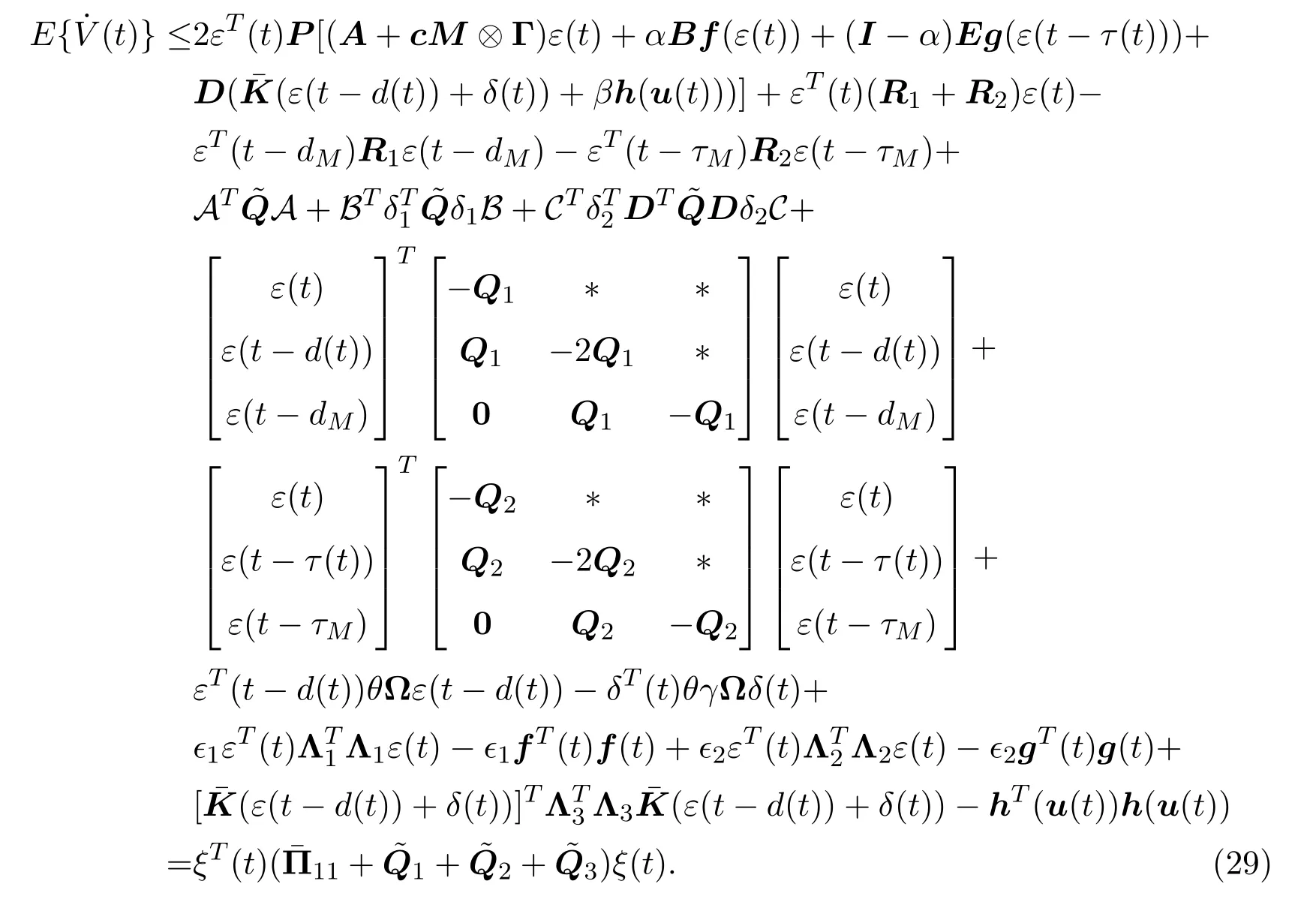
其中

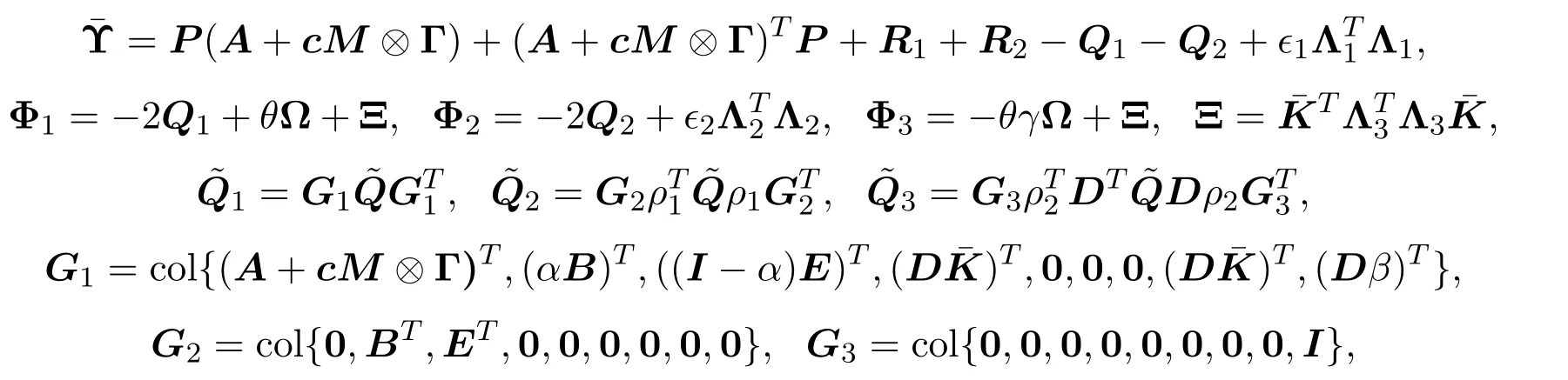
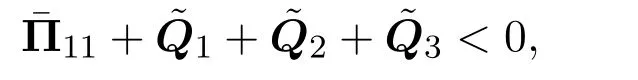
3.2 控制器设计

需要指出的是,定理3.1只给出了系统稳定的充分条件.在此基础上,定理3.2将会给出控制器增益Ki(i=1,2,···,N)以及自适应事件触发机制的参数矩阵

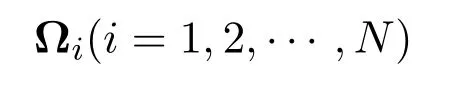
的设计方法.

定理3.2对于一些给定的正标量参数αi(i=1,2,···,N),βi(i=1,2,···,N),ci(i=1,···,N),ϵi(i=1,2),,τM=maxN{τi},κ,ι以及矩阵Γ＞0,A＞0,B＞0,E＞0,Λi(i=1,2,3),θ和γ,误差系统(11)是渐近稳定的,若存在对称矩阵X＞0,Y＞0,使得如下不等式成立:

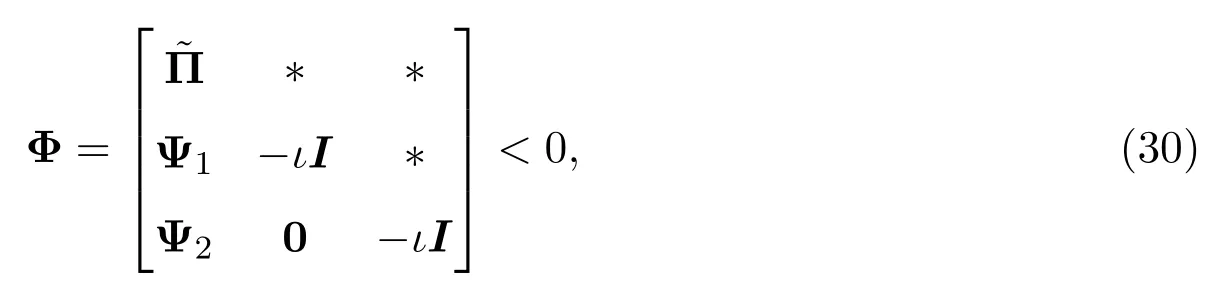
其中

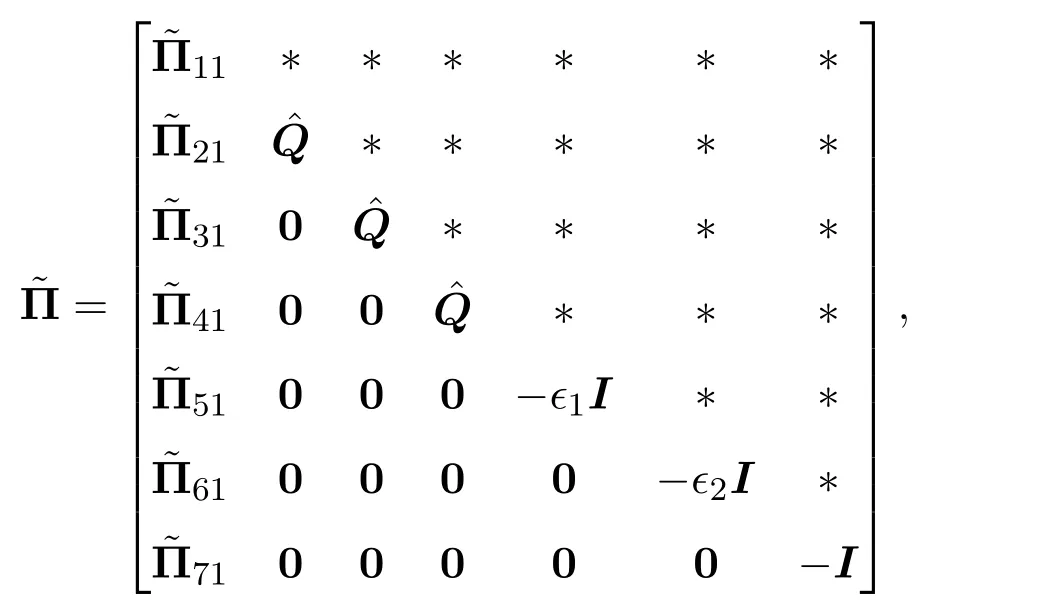
此外,本文设计的控制器增益和自适应事件触发参数矩阵分别如下:

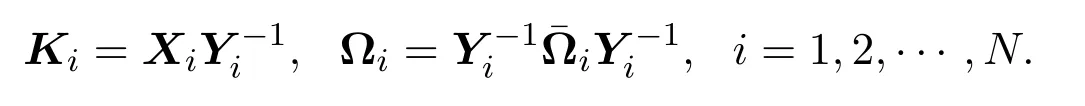
证明基于引理2.3,不等式(17)成立当且仅当如下不等式成立:

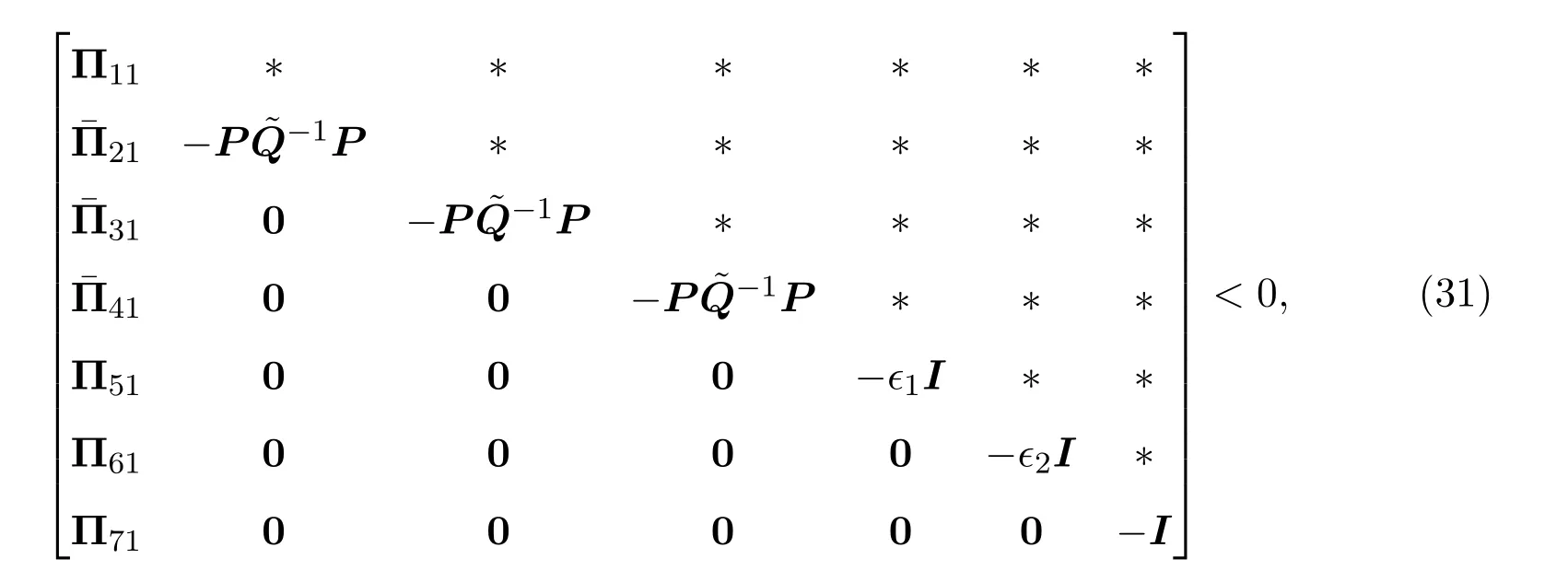
其中

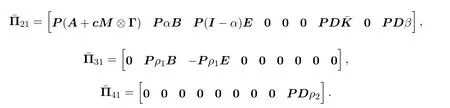
对任一标量κ＞0,易知如下不等式成立:

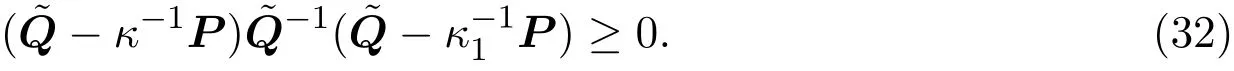
由此推得

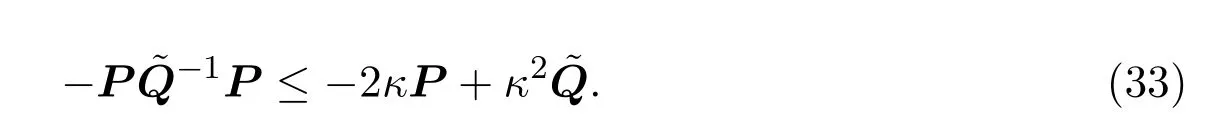
由此,易知不等式(31)成立,若如下不等式成立:

利用矩阵的性质,易知

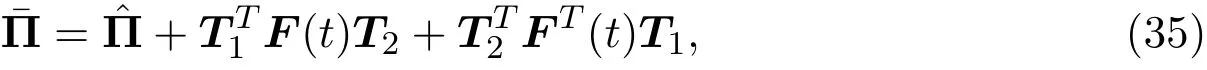
其中

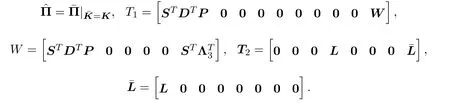
应用引理2.2,可知

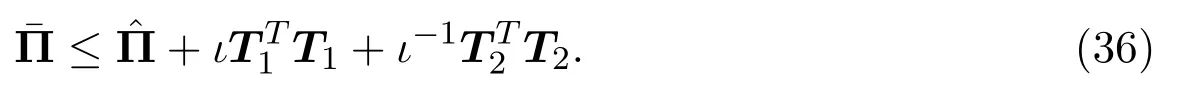
因此,欲证不等式(34)成立,只需证

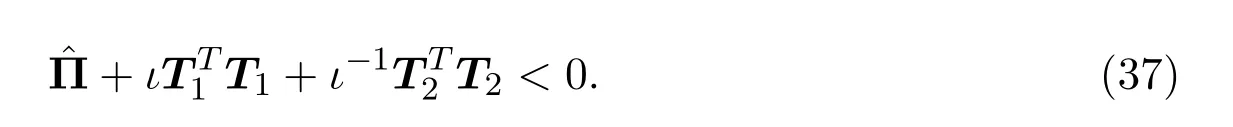
假设不等式(37)成立,根据引理2.3,可得

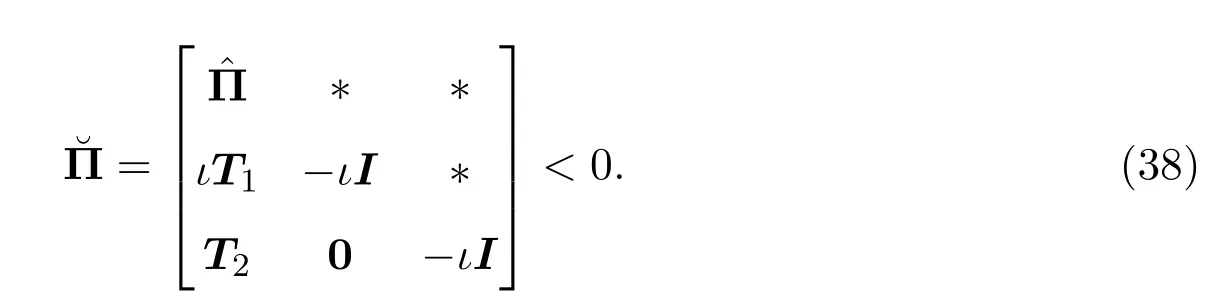
4 数值仿真

在本章节,提供一个数值例子来证明上述方法的有效性.假设复杂网络系统的驱动系统(1)以及响应系统(2)均是由三个节点所构成,且每个节点都是二维的,即有系统的外部耦合矩阵及内部耦合矩阵分别为

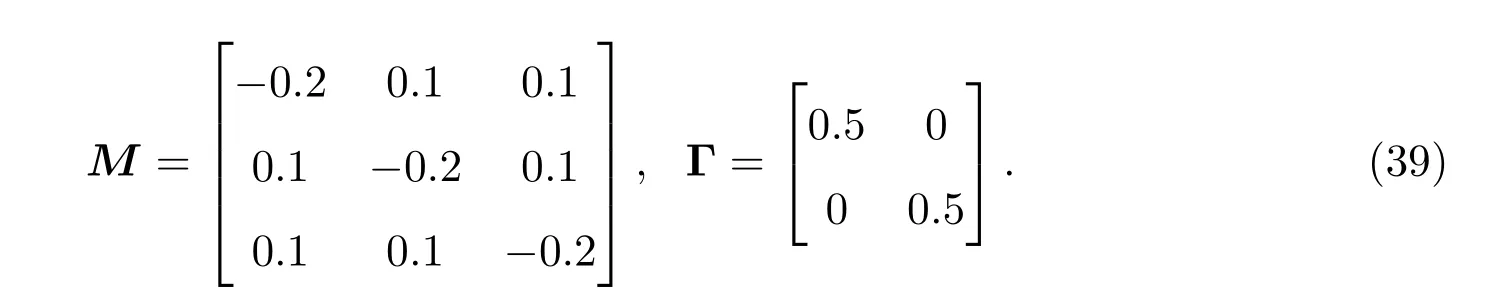
对于每一节点i(i=1,2,3),选择非线性函数f(xi(t))和g(xi(t-τi(t)))以及网络攻击的信号函数h((ui(t)))分别为

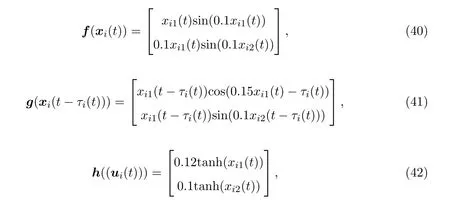
系统的参数矩阵分别取为

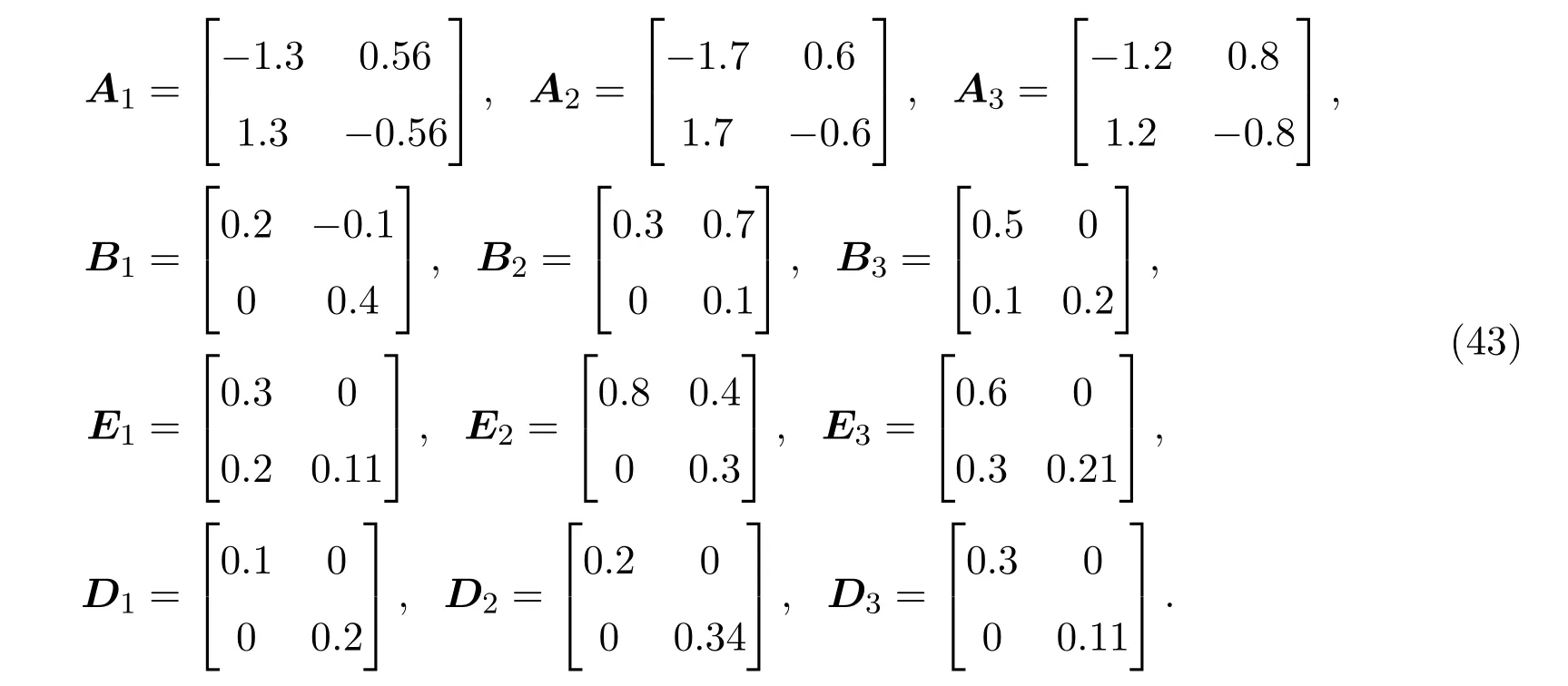
不确定参数矩阵分别为

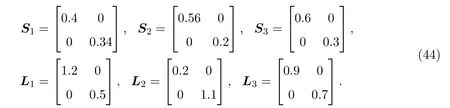
在本例中,确定节点动态行为的切换概率的期望为αi=0.6(i=1,2,3),网络攻击的概率的期望是βi=0.5(i=1,2,3),最大时滞为dM=0.15和τM=0.1,自适应事件触发机制的参数分别为θi=0.3(i=1,2,3)和γi=20(i=1,2,3),耦合强度为c1=0.8,c2=0.9,c3=0.62,其他参数为ϵ1=5.6,ϵ2=4.2,κ=3,ι=5.基于定理3.2,使用matlab软件里的LMI工具,可以得到控制器增益矩阵以及自适应事件触发参数矩阵如下:

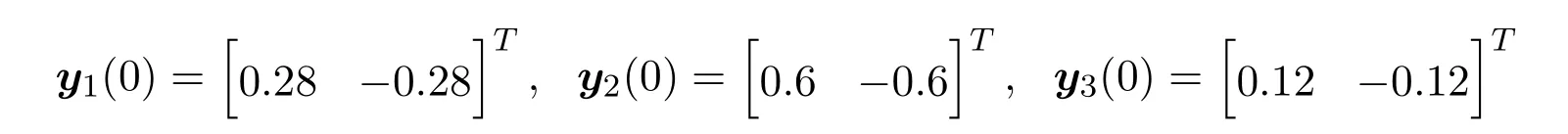
以及自适应事件触发的阈值参数分别为λ1(0)=0.26,λ2(0)=0.31,λ3(0)=0.164.对每个节点均考虑网络攻击以及自适应触发,得到的仿真结果如图1-5所示.图1-2分别展示的是加控制器和不加控制器时的同步误差信号的变化.比较这两幅图,就能发现当有控制器的时候,驱动响应系统的同步误差才会最终区域零，即系统达到同步.图3给出了自适应事件触发的时刻和时间间隔.从图4可以看出事件触发的阈值是变量并最后趋于常数.图5描述的是网络攻击信号的变化情况.以上仿真结果表明,本文所提出的自适应事件触发及控制器的设计方案是有效的.

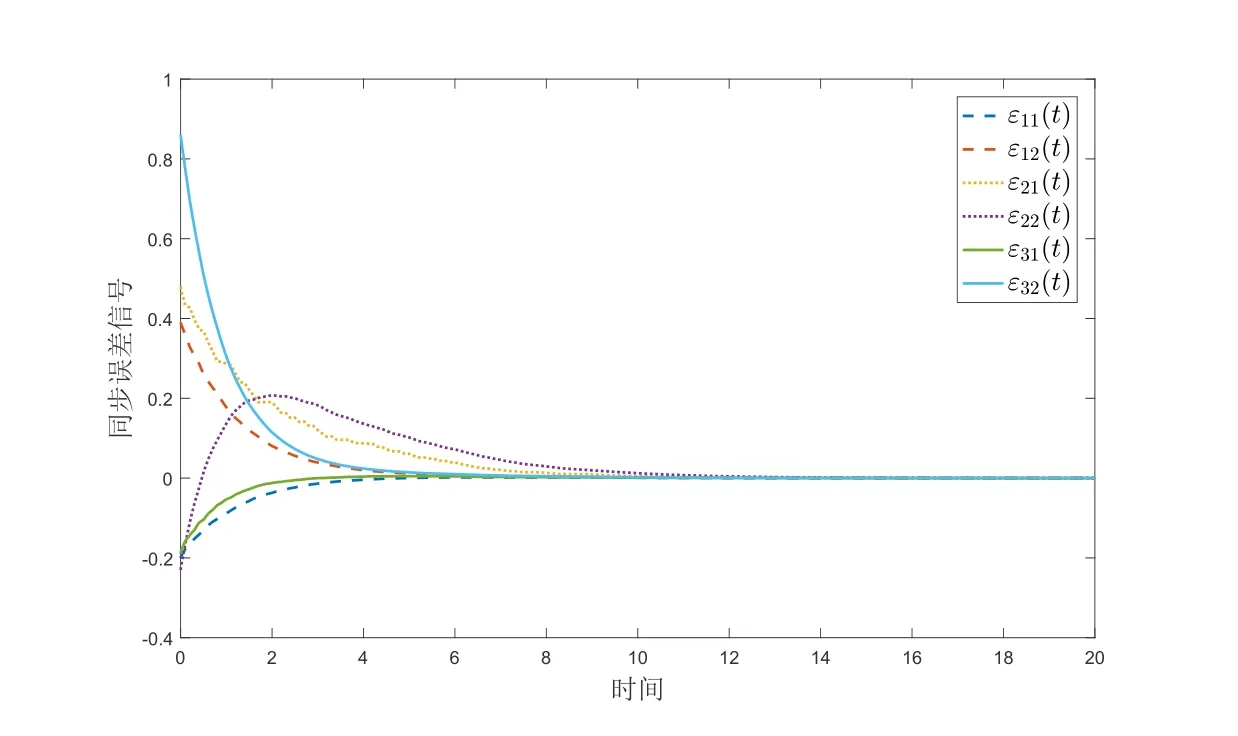
图1 有控制器时的同步误差εi(t)(i=1,2,3).

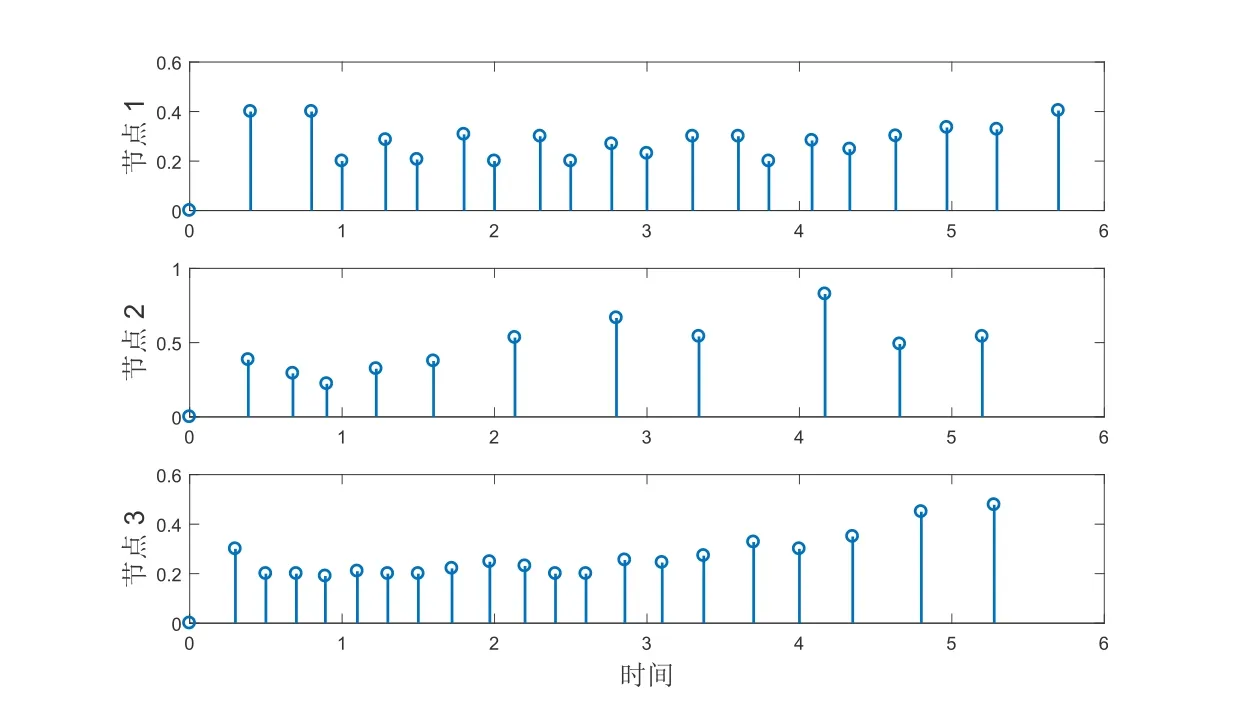
图3 自适应事件触发时刻以及间隔.

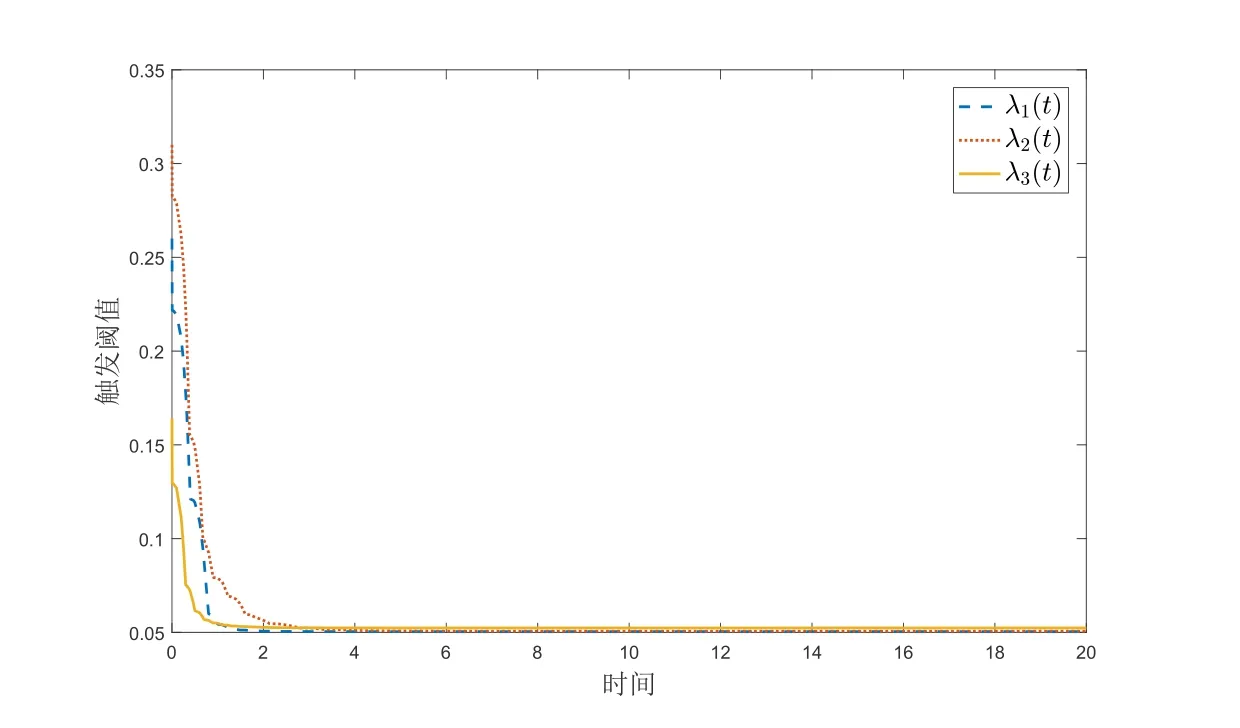
图4 自适应事件触发阈值λi(t)(i=1,2,3).

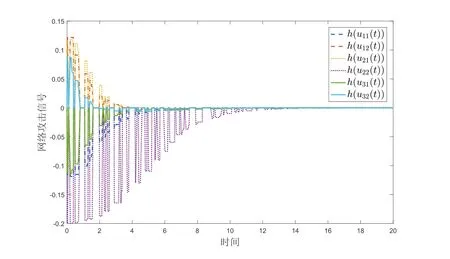
图5 网络攻击信号h(ui(t))(i=1,2,3).

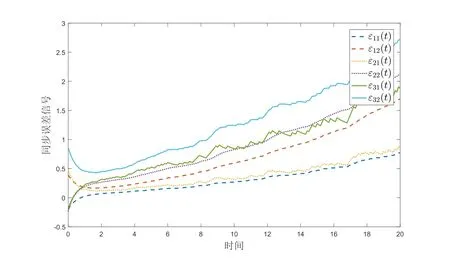
图2 未加控制器时的同步误差εi(t)(i=1,2,3).

5 结论

本文利用Lyapunov稳定性方法,借助matlab软件,研究了随机网络攻击环境下,具有随机动态行为和时变时滞的复杂网络驱动响应系统的自适应同步控制问题.在控制器增益变化及网络攻击能量有限的情况下,得到了建立的同步误差系统渐近稳定的充分条件.然后,通过使用线性矩阵不等式的方法,给出了控制器增益及自适应事件触发参数矩阵的设计方案.最后,提供数值仿真实例,以此验证本文所提方法的有效性.